-
Posts
534 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by DQW
-
That's your error (the underlined). Look at the other n-spheres again and you'll see what's wrong.
-
Those are merely colloidal dispersions of magnetic metals like Fe/Co. The hard part there is achieving the right particle size distribution - I would imagine you'd need micron-sized or smaller particles. Determining the best dispersive medium may be a little easier. You could try various media/concentrations to see if you can stabilize your iron powder (I hope it is a fine powder) in them. I would recomment a reasonably viscous medium as a starting point.
-
6E30 : If you tell us exactly what you have in mind, we might be able to make an appropriate suggestion. In what way do you want the fluid to respond to an applied field ? Most charged (electrolytic) fluids show little, if any, response to magnetic fields - primarily because there is no velocity field in a static electrolyte.
-
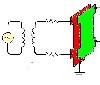
Force vs Acceleration graph - object in circular motion
DQW replied to JoeMK's topic in Homework Help
JoeMK : To draw a graph, first write out the equation that relates the two quantities. -
Just a guess here, but might it be because we only have a finite time to write down the decimal representation ?
-
And I shall try to make physical sense out of this, as you are clearly intending a physical, rather than mathematical explanation. Now, it is not clear whether this railway line runs on a plane or a large sphere, but I shall hold on this detail until it becomes necessary to proceed. Now either the lines are parallel, or they are not. This has merely to do with the space in which the lines exist and the definition of parallelism in that space. It should have nothing to do with my POV. In fact, in my POV, the lines appear to converge, so I would hardly call them parallel. Now physically, and ideally, everything up to the horizon is within sight, since it lies within my line of sight. On the plane, there is nothing beyond the horizon - from a non-zero height above the plane I can see every point on the plane and no point is obscured by another. On the sphere there is indeed a large surface area that exists beyond my horizon. And on the sphere, the railway line does indeed vanish from sight beyond the horizon. Since this is what you claim, it follows that you are talking about a situation on a sphere (or similarly closed 2D surface). Unless you are now talking about practical limits to sight from dispersion and minimal detectable signals, there is no difference between 'seeing' and 'significantly seeing'. But in this case can only talk about finite distances, so this can not be. Hence, 'seeing' is synonymous with 'significantly seeing'. A contradiction. On the sphere, the lines do not converge to a point. On the plane they do, but this possibility was previosly ruled out. So we are at an impasse and can not proceed. Please eliminate this contradiction by changing one or both of the offending statements.
-
The number of "states" is merely the number of dimensions in the space that describes the outcomes of an observation. Naturally, this depends on the "thing" that you are trying to observe or the property that is being measured. If you are trying to observe the aliveness of the cat, this is a two-state system (or a binary valued observable) : the cat is either alive, or it is not - and both outcomes are allowed by the physics of the problem. Hence, in the absense of a measurement, the "aliveness of the cat" (not the cat itself) may be described as being in a superposition of two states (it is the property which is in a superposition of states). Now the "physical nature of the cat" is not a space with infinite dimensions, simply because science does not allow it. Mass conservation, thermodynamics, etc. forbid the cat from turning into a sea monkey or an old man in a hat, so these are not allowed states in the space of "the physical nature of the cat". This space is spanned by only one state : "cattiness". (The subspace of the other states is a zero-matrix)
-
By the last question, I meant something like "is 4D space perfect for representing the taste of my apple", but nevermind. And thanks for the replies.
-
What ? I didn't understand a word there. Would you please explain what that was all about ?
-
If someone was talking about things that I was clueless about, I wouldn't have the gall to call him a "blind dog".
-
No he's NOT right. A beta particle is not "like" an electron - it IS an electron. Also, a gamma ray is not "like a photon" - it IS a photon.
-
True. I've seen this written both ways - just as is the case with the dielectric constant. Sometimes, the imaginary part (of the dielectric constant) is called the conductivity, other people call it simply the imaginary part of the dielectric constant. Likewise with the refractive index. The wave vector is, in general, a complex number. And the refractive index is proportional to the wave vector. But many times I've noticed that people write the real part as 'n' and the imaginary part is simply labeled [imath]i \kappa[/imath] or something like that (and as you said, is the origin of the decay term) . I can't back this up right now, but even between Jackson, Kittel and Ashcroft, I'm sure you'll come across both notations.
-
Yes, essentially your circle is divided into 2 segments by the two real points (0,0) and (2,0). One of these two segments is the required locus (the other segment contains points which map onto a slope of 5pi/4; note that tan(5pi/4) = 1 as well). You can determine which one of the two segments it is by simply choosing a convenient point from each segment and substituting into the given function to see if the equation is satisfied. I've actually done this for you in post #13.
-
Just click on the text and a window will pop up with the script in it. I get (leaving out constants like 1/3, pi, etc) : [math] V' = (1-f)^2 \sqrt{2f - f^2} + f^2 \sqrt{1-f^2} [/math] where [imath] f = \phi /2 \pi [/imath]
-
This is true. While I don't remember the numbers, I do recall that the analytic form for the dielectric constant has a singularity at [imath] \omega = 0 [/imath]. PS : I failed to mention before, that what is commonly refered to as the refractive index (n) is the real part of the square root of the dielectric constant. So, while [imath]\sqrt {\epsilon } [/imath] may be complex, n is generally real, but is still frequency dependent.
-
There are many more mistakes in his calculation. For one thing (if I'm reading the notation correctly), I don't see any square roots. The heights (calculated from Pythagoras) must involve square roots.
-
Yes, of course : v = c/n, not c*n Thanks for pointing that out. As for a typical value of n for a metal, I don't know anything off the top of my head, but we are now treading more murky waters. (i) For one thing, the refractive index ([imath]n(\omega)=\sqrt {\epsilon _r(\omega)}[/imath] for a non-magnetic metal) is a function of the frequency, [imath]\omega[/imath]. So, if you want to specify n, so must say what frequency you are specifying it at. (ii) The dielectric constant, and hence, the refractive index is in general, a complex number. At the very high and very low frequency limits, the dielectric constant [imath] \epsilon_r(\omega) [/imath] is essentially real (the imaginary part is negligible), but the refractive index can be real or imaginary.
-
Bobby, you have an error in your first equation (and several errors subsequenntly). It should read [imath]V = (1/3) \pi r^2 h [/imath], not [imath]V = (1/3) (2 \pi r) h [/imath] Please recheck your equations.
-
To practice, find the fourier transforms of some of the commonly found functions : the constant, the dirac delta, the exponential (e^{-kx}), the gaussian (e^{-ax^2}), the sine ( sin(kx) ), the single-particle coulom potential (1/x), etc.
-
Hoyle was sadly quite wrong as far as his SST went. Why is he trying this bio-stuff ? Poem by Barbara Gamow (wife of cosmologist, George Gamow) "Your years of toil," Said Ryle to Hoyle, "Are wasted years, believe me. The steady state Is out of date Unless my eyes deceive me, My telescope Has dashed your hope; Your tenants are refuted Let me be terse Our Universe Grows daily more diluted!" Said Hoyle, "You quote Lemaître, I note, And Gamow. Well forget them! That errant gang And their Big Bang- Why aid them and abet them? You see, my friend, It has no end And there was no beginning, As Bondi, Gold And I will hold Until our hair is thinning!"
-
While this model might apply to billiard balls, it certainly does not apply to electrons. In a case of a current carrying conductor, it is not electron-electron interactions that dominate the transport behavior. The electrons respond to the field that is set up in the conductor (by a rearragement of charges in the battery/voltage source), and this field propagates at nearly c (c over the refractive index of the conductor, n). Resistance to transport comes from (i)electron-electron interactions (ii)electron-phonon interactions, and (iii)electron-impurity interactions. At normal (300K) or high temperatures (and normal values of current density), the contribution from (ii) dominates the resistivity, while at low temperatures, (iii) dominates. The strength of (i) is orders of magnitude weaker than (ii) (as evidenced by the low resistivity of an electron beam in an accelerator, for instance) and this is the reason why you can have pretty accurate descriptions of electronic properties (of many normal materials) by simply neglecting many-body effects. It's not too hard to come up with a plausibility argument for the negligible contribution of electron-electron interactions to the resistivity. Consider a pair of electrons whose line of approach is along the direction of current flow. If the first electron "collides" with the second, making the second electron speed up (gain momentum), the first electron itself must lose the same amount of momentum. So, one electron speeds up, while another slows down. The average effect is that the current remains unchanged. Hence, the negligible contribution of electron-electron collisions. A better model is to describe a current using a vertical pipe filled with billiard balls (or a liquid). The billiard balls fall through the pipe because they are responding to the gravitational field.
-
I'm guessing it comes up very often because a system of equations has non-trivial solutions only if the determinant vanishes. This has great importance in eigenvalue problems.
-
I can't follow any part of this. What is it that you want to have "converge" on the circle ? And why ?
-
Philosophical ? I would have used another word ! It looks like most posters here don't read previous posts carefully; else there would not be statements like "infinity is not a number; it is a concept". To repeat what matt said (only in slightly different words, and far too loosely, I imagine) : "Infinity" is a number; only it is not defined in the Reals (the set of real numbers), just as 0.75 is a number that is not in [imath] \mathbb{Z} [/imath] (the integers). One way to define it (I think) is simply as the OP put it - it is a number [imath]\aleph [/imath], that satisfies [imath]\aleph + k = \aleph [/imath] for any real k. The mathematical definition of "infinity" has absolutely no basis in time, space, or Buzz Lightyear

