tar

SwansonT, The radial/tangential direction is somewhat ambiguous, looking at some of the videos on the internet of motorbikes being used to spin small roundabouts. The people have their legs on the other side of the center of rotation, and their shoulder blades and arms near the circumference. Each part of their body is describing a different circle, so there are an infinite amount of tangent lines to consider, even at one instant. All these infinitely numbered tangent lines, however, are still normal to the radial line that would describe the center of the person's body. What is interesting to me, is that the tangent lines can be drawn in both the direction of motion, and extend back in the other direction. The normal to these tangent lines is the radial line. When the young man slides over the bar in one of the videos I watched, his body is extended out radially from the roundabout. That is, it appears as if his feet clear the ring, at the same time. It happens very fast, and he stays in relatively the same orientation to the rider that remains on the ride, as he flies off and winds up on the ground, "outward" from the center of rotation. So, what combination of forces, moments of inertia and cavity positioning, makes the fluid in the inner ear gravitate to the bottom of the cavity? Regards, TAR

SwansonT, A reactive centrifugal force is taken into consideration when a propeller designer calculates the stresses and strains within the material. I read that inorder to analyze this, the engineer breaks the propeller into concentric rings of material, with the one ring acting upon both the ring on the inside and the ring on the outside. The reactive centrifugal force acts on the ring toward the inside, and the centripetal force acts on the ring to the outside. This analysis is not unuseful when considering the boy on the round-about. The position of the fluid in his inner ears is what is informing him of which way gravity is, and which way he is being "pulled". Which way he will "fall" if he lets go. This is where the rigid body analysis of the situation is somewhat limited, because it does not consider the position of the fluid in the inner ear of the boy. The motorcycle rider we were talking about before leans in the turn to put the bike between her and the direction her inner ears is telling her is down, the direction she will fall if she does not keep the bike and her ears balanced and normal to this "pull". The fluid in the inner ear is also trying to fly off on a tangent. Like the water at the bottom of the bucket on the end of the rope, it will settle at the bottom of the bucket, and the bucket's bottom is not pointed along the tangent, it is pointed normal to the tangent. It is pointed radially outward. Regards, TAR Thread, I have not yet looked at pictures of children on a circulating roundabout, but my specuation is, going by my memories as a child, that a not unusual position would be "braced against an outward pull" with the top of the head facing toward the axis of rotation and closer to horizonal the faster the round about is going. My speculation is that the body wants to be "upright" in respect to gravity, and where the fluid in the inner ears is, is the direction this 'down' is thought to be. Regards, TAR

Pzkpfw, No, not evidence of a force that does not exist...but the clay ball at the end of toothpick is not unlike my 10 year old head on the playground roundabout. Earlier, it was suggested that the human instrument, was not sufficient to measure forces and the direction thereof. I am only submitting evidence that the toothpick tipped outward, and looking at the path of the tip, evidenced by the slot in the clay, where it stood and fell, the slot is a radial line, and I only applied a tangential force to the circumference of the ring. Somehow, the inward force, the centripedal force and the inertia of the blob, both the stationary inertia, and the tangential inertia, conspired to move the blob radially outward. No force was applied in that direction, but that is the direction the toothpick, tipped. Regards, TAR

had some upload issues 1. SwansonT, Right, the tangent is the straight line. And there is no force directed radially outward, according to F=Ma, except my toothpick tipped radially outward, for some reason. Just trying to figure the reason. Regards, TAR

Pzkpfw, OK, the centripedal force is too small, and the thing tries to go in a tangent, instead of straight line, but it sure "looks" like the thing is trying to go radially outward. I took a disk of clay and stuck three verical toothpicks in it with three balls, small medium and large on it, and attempted to spin the disc in a horizonal orientation on a pen. More of a start and stop, and I could "feel" the inertia of the large ball trying to not get moving...but the large ball wound up tipping the toothpick radially outward. I then made three same size balls and repeated the experiment. They toothpicks were too deep in the clay, provided enough centripedal force, and the toothpicks did not tip. I put the toothpicks in the clay only half as deep as before and repeated the experiment. They all three tipped outward. One radially outward, one a little behind radially, and one a little ahead of radially. There seems to be another aspect to this discussion to consider, and that is the force that starts the disc spinning and overcomes the inertia of the stationary disc. The force I applied to the clay was a repeated tangential force on the circumference of the disc. Each pulse coaxed a slowing disc from its slowing condition, to a pulse that coaxed it in its circular rotation. Once the toothpick started to tip, the ball was "outside" its original circle and its original tangent line and its moment of inertia, wanting to "stay" out there, seems to cause the toothpick to tip even more easily outward. Mike, Here is a picture illustrating what I was mentioning earlier about the centripedal/reactive centrifugal force NOT being exactly counter gravity, in New York. The one toothpick points toward/away from the center of the Earth. The other toothpick points toward/away from the axis of rotation somewhere between the center of the Earth, and the North Pole.

Thread, This link clarifies things for me a bit. http://en.wikipedia.org/wiki/Reactive_centrifugal_force I think, my experiences on the playground turnabout, and my muses about storing energy in concentric rings making up a flywheel, with pins that engaged the next outer ring as the speed of inner ring caused its pins to protrude into the catch groves of the next outer ring, are experiences and ideas that are dealing with reactive centrifugal force. SwansonT is only talking about inertial centrifugal force, which is an apparent or ficticious force that "looks" like a force is acting, from the point of view of an observer in the rotating frame, that does not exist when observed from an inertial frame. The ball looks like its curving under the influence of a force, but its really going straight, making the apparent force, a fictious force. On the other hand, a reactive centrifugal force really does enable a centrifugal clutch to operate, as each component of the restraint, that causes the acceleration of the body that wants to go in a straight line to follow a circular path applies an equal and opposite force to the "ring" or piece of the constraint closer to the center. Regards, TAR So one should not use the term centrifugal force without specifying if they are talking about reactive centrifugal force, that is countering the centripedal force at every integral of the constraint, or if they are talking about apparent, or inertial, or ficticious centrifugal force.

SwansonT, OK, no net radial outward force, if an object is moving in a circle. How about if an object is moving in a spiral? With an increasing distance from the center of the spiral? I am not sure if you can have a tangent to a spiral, but it seems if you do, such a tangent is not normal to a line drawn from the origin of the spiral, but it has an outward component. When dealing with the playground merry-go-round, it is harder to cause your body to follow an inwardly directed spiral (pulling yourself closer to the center) than to relax your arms and slide or lean outward. When holding fast to a circular path, your hair and loose clothing and blood seems to be drawn outward. There is this situational result of everything wanting to maintain its inertia that makes the outward spiral more likely to occur than the inward one. It takes effort or force to maintain the circular path, more to pull your body closer to the center. The net force might be directed toward the center, and there is no force directed radially outward, but if there is motion along the path of a larger and larger spiral, then some component of the net force on the object must be directed outward. Well, maybe not must, but the straight line inertial momentum causes the spiral to widen. Regards, TAR

SwansonT, "Except that it isn't. That's a misconception you have. You would travel tangent to the circle, not radially outward." On the playground carosel, if I lost my grip for a moment (clinging to a point near the center of the merry-go-round) I would slide outward on the deck, increasing the radius of the circle I was traveling and getting further from the center. I would have to fight inward again, pulling toward the center. What Robittybob1 and I are stuck on, is that during the release, when you go off in a tangent direction, you are still attached to the deck by a little bit of friction, and take on some of the tangential directional attributes of the deck as you slide out through the concentric, larger and larger circles. The motion outward is effectively an outward trek. As you attach yourself to a bar circulating at a larger radius, it gets harder to hold on and your adreneline shoots up and you beg the pushers to slow the thing as you do not wish to continue the outward trek, past the outer circumference of the ride. If, when determining whether your direction of motion is tangent or radial you were to be on a rotating disc 100 meters in radius, and you were to draw a line on the deck from your position near the center where you let go (you are wearing teflon clothing and the deck is oiled and there are no holding points past a meter out,) to the point where you are on the 50 meter circle, you would find that your direction of motion through the 50 meter radius circle line, would be roughly normal to the tangent line drawn at that point. So, when determining the direction a fella goes in when he falls off the carosel, one can figure a direction tangent to the outer circumference of the ride. But what direction is he going when he is still on the ride, but being pulled toward the outer circumference? Regards, TAR

pzkpfw, Well OK, if the force ON the object is what we are counting, and the momentum does not count as a force, because an object in constant linear motion requires no further force to maintain such, then the "pull" on my arms as I hold on to the carosel is my arms pulling me inward, and no force is pulling me outward...except outward is where I wind up should I let go. Robittybob1 seems to be stuck on the same idea I am, in terms of the tangent motion being "away" from the circle. In the video the cut string allows the ball to go up tangent to the circle, but if you imagine an elastic thread still attached to the ball and the center of the circle, one can imagine the thread on a line radially outward from the center which seems to maintain for close to a quarter turn of the wheel. For instance, let's say a lasar pointer is attached to the center of the wheel, which keeps turning even after the string is cut. If the laser was pointed at the ball, would it continue to shine on the ball, after the string is cut and the ball flies off on the tangent? At least for almost a quarter turn. Regards, TAR

Hum, I suppose the defintion of force on an object, as opposed to inertia within an object is at the root of the problem here. If a force causes an object to move, and an object is moving in a straight line, the force has not disappeared, it has been transferred to the momentum or inertia within the object. That force, is the "pull" you feel on the rope, with the rock at the end, that you are swinging around your head, in a circle. While the direction that the rock goes when it slips out of your knot is a straight line tangent to the circle you got it going in, you had to get it going in the circle by getting the rope to go taught. And you have to get the rope to go taught by lifting the rock off the ground against the force of gravity. Then you coax the rock in a small circle around your feet by inscribing a circle with your hand around your head, with the other end of the rope, in it. Letting the rock "fall" in only one direction tangent to the circle you are inscribing around your head as you move the fulcrum point of this one way pendulum in the circle around your head. You keep leading the rock, faster and faster, in this manner, pulling it in a tangent to the circle direction, by utilizing a combination of its weight (the force of gravity) and its momentum (desire to continue in a straight line). The rock's momentum, when you get it going fast enough to "lift" above your waist, "feels" like an outward pull. When it slips your knot or you release it like a rock from a slingshot, it goes in a straight line, tangent to the arc at the moment of release, but it travels away from you, effectively "radially outward" from the circumference of the circle you were describing. Regards, TAR

SwansonT, I have no problem standing straight up in New Jersey either, but the circle I travel around the axis of Earth every day is a smaller circle than the circle traveled by someone that lives on the equator. If I would visit the North pole, and be on the axis, I would not travel a circle, I would just face 360 different degrees, all of them facing South. We are here, in this problem, considering why there is an apparent "outward" force, that counters gravity in an opposite gravity direction, caused by the angular velocity, or moment of inertia of an object traveling in a circle, along with the surface of the Earth. This effect, if present, should be different on the equator where the circle is large, than at the North Pole, where the circle is so minimal as to not be considered a circle. I have seen various figures that indicate a mass weighs less when spinning with the equator, than when hardly spinning at all on the North Pole. Some say a 1 in 200 difference, some say 1 in a 1000, but all the figures indicate the spinning thing weighs less which suggests a force "lifting" in the opposite direction as gravity. Speculative interpolation would make me guess that the 45 degree measurement would come out heavier than the equatorial measurement, and lighter than the pole measurement. The "force" though, caused by the spin at 45 degrees is not opposite gravity, like it is on the equator. It is pointing South of normal. Speculation would have me guess that although you have no problem standing at 45 degrees latitude, the force "countering" gravity at the equator is not countering it at 180 degrees in New Jersey, but countering it at 135 degrees. At the North pole the force of gravity is being slightly countered at 90 degrees. Regards, TAR

SwansonT, Sorry about wheigh and centripical. I realize those kinds of mistakes are annoying and tend to highly devalue any thought I might be trying to express. I should be more correct. I was looking this morning at pictures of the magnetosphere, trying to get the directions of radially outward and tangentially positioned, straight in my mind. When thinking about the circles tranversed by a object sitting still on the surface of the Earth, it occurred to me that the tops of our 36,000km towers inscribed differerent size circles in the sky. The one on the equator with the largest radius and the one on the North Pole, with hardly any radius at all, and the one built at latitude 45 degrees North with a radius somewhere inbetween. The 'lines of force' that eminate from the Earth are going in what direction, would you say? Radially outward, or tangential? Or some combination. The circle inscribed by the 36,000km tower at 45 degrees has a center, but it does not correspond to the center of the Earth. The center is inside the Earth but halfway or so toward the North pole. Radially outward lines from this cirlce would fall all in the same plane as tangent lines from this circle, but the plane of this circle is parallel to the plane of circle inscribed by the top of the equatorial tower. The tangent lines and radially outward lines from the North pole circle get hard to envision, since we are back to the headache of envisioning lines tangent to a point and the circle is a point, which either exists or doesn't depending on the way you look at it. What does it mean for a circle to have a radius of 0? And can you go radially outward, if you have no radius? Regards, TAR

Thread, I think my problem stems from not understanding why the inertia of an object in motion is not considered a force, in and of itself. If an object was not moving, a force would be required to overcome the stationary inertia. Once moving, a force would be required to deaccelerate the object and bring it to a stop. In the case of a orbiting object, the thing keeps falling toward the Earth...and missing. If it would not miss, then I could understand the force toward the center, the centripical force, was the only real one being applied. But the fact that it does miss, indicates to me, that there is a force being applied on the object that is causing it to miss the center. An outward force. A tangentially outward force. Like the tangent to the lifesaver, taking you outward, away from the life saver, 90 degrees later. I have been musing alot with a 1/4lb. sphere of clay in front of me. With a toothpick, drawing lines and angles, great circles intersecting at various angles. Interesting to note that a sphere can be divided into 24 60/60/90 triangles. I mention this, because two lines drawn at a 60 degree angle to each other wind up crossing each other exactly once on the diametrically opposed side of the sphere. Same thing happens if you draw two great circles intersecting each other at 90 degrees. Point being, what is true on one side of the sphere if continued to the other side, is upside down and backward, but exactly the same relationship, halfway round the sphere, as long as you are dealing in great circles. So...when talking about a simple circle, and something tangent to it, or normal to the tangent, and you consider the direction a force is acting in, a quarter period later, what was tangent is now radial, and what was radial is now tangent. When you are swinging the bucket on the rope, the water does not come toward the rope, it goes toward the bottom of the bucket, which might be because it wants to go tangent to the circle, and the bottom of the bucket keeps getting moved into that path...or it wants to go radially outward, and the bottom of the bucket is alway positioned radially outward from the rope. Regards, TAR

SwansonT, Oh, I thought we were saying earlier that the mass would wheigh less at the equator, more at the axis. I remember some link or search I read wrong, then. I thought the ton of stuff wheighed at the equator would wheigh 2002lbs. at the North Pole, without the tangentially pointed inertia of the angular velocity caused by moving along with the surface of the Earth, "lifting" it away from the surface. Regards, TAR There was a brief exchange of thoughts as to "why" a thing wheighed less on the equator than on the pole, but it was never suggested that a mass does not wheigh one part in a thousand less on the equator, than on the pole. SwansonT, By my rough interpolation of what I thought were the facts, a ton wheighed in NY would wheigh 2001lbs. on the North Pole and 1999lbs. on the equator. Is this not true? Regards, TAR

SwansonT, I was counting the the real number 1 World Trade as an example at around 45 degrees, the one on the equator as an example at 90 degrees and the one on the North Pole as an example of a tower on the axis of rotation, that should not have much of an orbital velocity at all...unless the change in orientation counts as an acceleration. That is 6 different places to consider what forces are on the wheighed mass. The forces normal to the center of the Earth in each case, if different, are caused by centrifugal forces generated by the inertial momentum of the object due to angular velocity which is large at the equator, medium in NY and minimal at the North pole. Or so my speculation would go. Regards, TAR So, with our 36,000km tower...what if we built one of those on the equator, one in NY and one on the North Pole. What would happen to an object released from the highest point, in each case?

Mordred, OK, the two situations do not overlap...except...if you were to build a 35 thousand km high tower and release something from its highest point, would that something be in geosynchronous orbit? Regards, TAR Does an object at the top of number one World Trade have a different velocity than an object on the first floor? A different speed? A different acceleration? If we built a replica of the tower on the equator, and another on the North pole and wheighed a standard mass on the first floor and the top floor, would there be a difference in the whieghts taken in the six locations?

SwansonT, Definitionally, how close to the Earth's equator can you be an object in geosynchronis orbit, before you are an object standing on the rotating surface? Regards, TAR

Thread, If you make a great circle on a sphere in red, and then make a hole somewhere on this circle and through the hole make another great circle 60 degrees (120) offset, in yellow, you get the two lines crossing each other twice, making two Xs on the sphere. Halfway between the 120 degree sides of the Xs, make another cross of a blue and green great circle with a similar X having the 120 degree sides of the Xs oriented toward each other. You will have just inscribed a spherical cuboctohedron on the sphere, with 6 square areas and 8 triangular areas evident. Each of the four colored lines, represent the plane of each of the four intersecting hexagonal planes we have been taking about in the dual Cuboctahedron/Spherical Rhombic Dodecahedron. If you wander 30 degrees NEish from the hole, along the red line and make another great circle in red intesecting the first red line at a 90 degree angle and repeat this 60 degrees along the red line later, and then again in another 60 degrees the three new red great circles will divide the sphere into 6 "orange" slices, each divided in half by the first red great circle. Attempting this placement of new yellow great circles at 90 degrees to the 30 degrees from the hole mark. 90 degrees from the hole and 150 degrees from the hole mark along the first yellow great circle, one finds the first new great circle can be marked in yellow, the second new great circle is already present in red and the third new great circle can be marked in yellow. Attempting marking the blue great circle with three evenly spaced great circles in the same manner as before one finds the first great circle already present and marked in yellow, the second great circle can be marked in blue, and the third great circle is already present and marked in red. Attempting to mark the green great circle into its six segments with the three great circles dividing the sphere into six "orange" slices, one finds the new great circles already placed and marked in yellow, blue and red respectively. Figure shown here is the result of following this procedure, with black diamonds inscribed on the inside of certain of the great circles, indicating where the 12 diamonds of the Spherical Rhombic Dodecahedron fall. Regards, TAR

SwansonT, Then why, when I wheigh myself, is it not the scale pushing radially outward on my feet? Regards, TAR

Mike, The stability when moving on the bike has to do with the gyroscopic effect the spinning wheels have. Here another inertia is taking place and the spinning mass of the wheels wants to stay in the orientation they are in. I have had a small gyroscope since I was young that I still play with. Pull the string and get it spinning fast and you can "feel" it trying to keep its orientation as you try and tilt it . A body in motion... Regard, TAR With my little gyroscope the resistance the spinning thing has to my attempted tilt, "feels" like a force resisting my attempted tilt. That the inertia of a mass, does not count as a force, when it feels so much like one, is the thing that is at the crux of the question of this thread. As an aside, I had a thought 15 or 20 years ago that you could design a flywheel system made up of larger and larger rings where you could store large quantities of inertial energy if you got the whole complex spinning really fast...then I figured...wait a minute, the vehical wouldn't want to turn, because you have this giant gyroscope going. Then I thought you could have three flywheels at different orientations counter acting each other...then I figured...wait a minute, then the thing wouldn't want to move. The spinning space station creates a radially outward "force" that feels like gravity pulling in the direction of a spot on the outside circumference directly opposed to the axis of rotation, or radially outward.

SwansonT, My mistake. A change in direction at a constant speed IS a change in velocity. But I am still stuck on tangential and radially outward, in terms of the fact that both directions take you away from the center of the circle. Not that I don't realize that the two directions are orthogonal to each other, but if you put a lifesaver on the ground and travel at 30 miles an hour tangentially to it, after a minute, you will be half a mile radially outward from the center of the lifesaver. Our being fooled by the motion in a circle, might be related to the fact that tangential motion results in a separation from the center as surely as radially outward motion does. Just at a different rate of separation. Significantly different rate at first, but as you travel a distance greater than the diameter of the circle, the two directions both take you away from the center of the circle at an increasingly similar rate. In the round-about example you wind up rolling/running/sliding away from the thing when you fall off, and in the bike example, you wind up off the road to the right. In either case you can draw a radial line, from the center of the circle, to where you lay on the ground. You can also draw a tangential line from where you lay to where you left the circumference of the circle, but where you would have been, still upright on the round-about or bike, had you not fallen, is on the radially outward line, where you lay. Regards, TAR Perhaps this "where you would have been" is important in explaining why the tangential launch, feels like a radial motion. Watching the kid you were crouching next to when you fell off, stay between you and the center of the thing, as you increase you distance from the center as you run/fall off, makes it seem like a radially outward manuver.

SwansonT, You Except in our example the acceleration is not a change in velocity, its a change in direction. The force is counteracting the momentum of the body, which would take it in a straight line tangentially away from the circle. The net force is toward the center but the net movement is in a path along the circle, which is the resultant path of the tangential (outward) momentum and inward force of the tires against the road. I am not trying to overturn any math. Just trying to explain why a person feels like they are being pulled away from the center of the circle. Regards, TAR

SwansonT, Circles are confusing. I was not so much trying to redefine the circle, as trying to figure if it made any sense to consider a relationship between moving radially outward and moving tangentially to the circle, since the one direction becomes the other, 90 degrees later. Instantaneously speaking you might be able to say a direction is either tangent to the circle or normal to the tangent line, but in terms of "feeling" a force, the feeling comes over time. I understand that if an inertial body maintains its speed but changes direction an acceleration must be occurring. In the case of the bike rider this force is applied radially inward, turning her momentum left, in the example. But that impulse to keep going forward, that is being conteracted by the force, the reaction of the tire against road, is a real impulse. The inertia is real. And this inertia starts heading to 360 and winds up heading to 270. The inertia lines at each point in the turn are parallel to 90 degrees worth of radial lines. If you would make a complete circle a couple of times and draw lines in all the directions tangent to the circle, and all the directions radially inward from the rider and bike, and all the directions radially outward from the rider and the bike, you would get three identical sets of directions. A vector is a direction and a magnitude, you can not get far unless you take some time to do it. An instantaneous figuring does not allow the human instrument the time it takes the human instrument to sense and remember and compare. It might "feel" like you are being pulled outward, because in total, you are being pulled outward. Regardless of the forces causing a change in your direction of movement when figured instantaneously. Regards, TAR The spring in Mikes spinning bob example is pulling inward. But something is stretching the spring. Which "looks like", over time, an outward force.

SwansonT, I noticed the vectors never intersect the center of the circle. That is why I concentrated on the point outside the arc of the bike, where the North (360/0) vector and the West (270) vector intersect. If you draw a square, centered at the center of the circle, with the upper right corner of the square being the point where the North and West vector intersect, all the vectors intersect all the other vectors somewhere to the upper right of the circle and to the lower left of this corner point. The "center" of the turn therefore may be considered the average position of these vector intersecting points, which by rough estimation is about 80% the way between the center of the circle and the square corner point. This as opposed to the roughly 70% of the way out that the bike is, halfway through the turn, when it is directly between the center of the circle and the square corner point. Each of the directional vectors found by drawing tangents to the circle at each degree position of the bike and rider has its parallel conterpart going radially outward in the NW quadrant of the circle. The rider leans into the turn. She leans left, toward the center to counteract something carrying her and the bike outward. Regards, TAR But, while I admit I am doing something wrong here, and the actual centripedal acceleration is being caused by the reaction of the tire and the road, and the rider is leaning merely to maximize these forces, allowing the change in direction to take place, I am still "speculating" as to why it "appears" that there is a radially outward "thing" going on during the turn. Interesting to note that if you follow a tangential line away from the circle it intersects all 90 of the degree radials to its left (or right if you are going the other way around the circle.) These intersections are rapid at first and get more and more spread out as you go. But as Mike pointed out, each of these intersections is further "out", radially speaking.

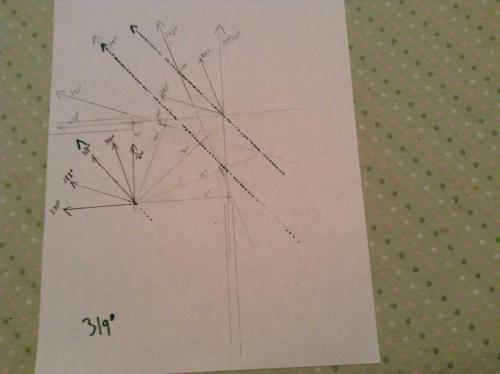
SwansonT, So what direction are you moving when you are going in a circle? If I draw a line depicting my motion tangent to the circle, for every degree of my turn, I get 90 different directions that look sort of like a fan. The lines all go radially outward from where you would hold the fan. Regards, TAR During the turn your momentum is heading toward 0, 359, 358, 357...273, 272, 271 and finally 270 degrees (West). The lines all trace back to 90 origins on a small 90 degree arc of the circle that the turn is part of. If you draw a circle with a center where the 0 degree tangent line, and the 270 degree tangent line meet, all the directions inbetween can be seen as radial lines drawn out from this point. While there is no arrow taking the rider East, there is an arrow eminating in each direction between North and West. And each direction can be seen as being in the same direction as a radial line drawn from the center of the curve. And in each case, following the line, in the case of gravel or ice causing the tire to loss traction with the road, will take the rider and bike off the road, to the right, to the outside of the circle of the turn. The momentum will take the rider and bike, radially outward.