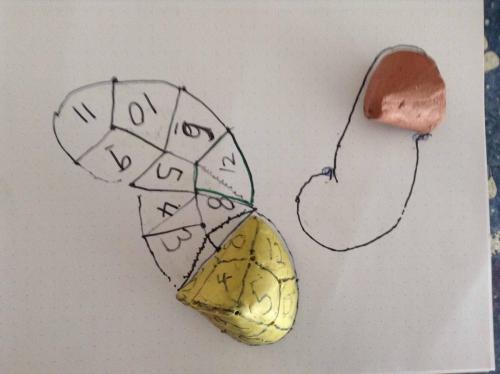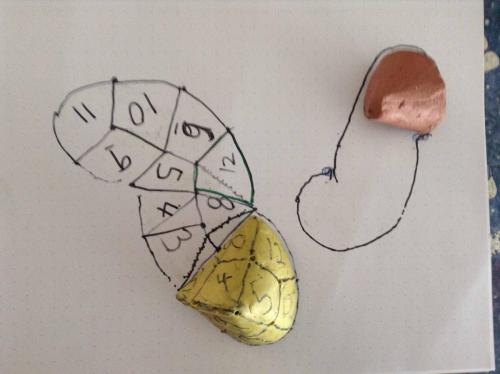tar

Thread, I took a purple, orange and lime green marker to follow the lines around my equilateral triangle, on the surface of the green sphere I made, marked out with the spherical rhombic dodecahedron diamonds. Was expecting the lines to meet in some funny zig zag way, like following the lines around the tetrahedron. Little did I know, that I did not have to make any twists or turns at the three points. Simply drew three straight lines through three of the four points on the sphere. Turns out, the point of the 1,6 and 10 diamonds(shields) is the same point and the three lines that define the equilateral triangle are a line from this point to the tip of the 8 a line to the tip of the 3, and a line to the tip of the 4. Enough words. Take a look. Its so simple and beautiful I don't know why I was not taught this in school.

SwansonT, Well I suppose it is absolutely evident that the universe is composed of mostly stuff we will never interact with, in several senses. No harm in finding that out mathematically and pointing it out. However the stuff that is currently "out there" in the cosmic present, is also right here, within our grasp, as we look up at it and see its arrangement and sense the frequencies of the photons and their energy and their vector, and build from that a model, an idea of, the place. In one sense, the cuniform is what we hold as the model. It represents the place, in an analog fashion. It is interestingly more important that we deal with the universe on the basis of the photons coming in from it, than consider it happening some other way. Regards, TAR Mike, Just so you know. If you take three spherical rhombic dodecahedron diamonds and put them together at their 120 degree points you have a 1/4 of a sphere. Exactly the same as one finger or thumb in the gum ball tetrahedron illustration. Or another way to look at it. If you take two quarters of a sphere and put them together you have a PacMan with its mouth open looking shape. You make another identical PacMan with the other two quarters, turn them 90 degrees (orthogonically) and have them try to grasp each other, and you get your sphere back. Regards, TAR

Mike, Nice. I will have to read up on Euler. I liked in particular in the diagram of the last scattering, the two instances of the four spheres forming the tetraheral pattern. Simplicity forming complexity and vice-a-versa. Like (non-sequitur here) in my last year long investigation of the spherical rhombic dodecahedron and its internal relationships, I finally realized the internal pattern was that four ball tetrahedron. Something every 10 year old is aware of when they take the gum out of their mouth and press it solidly between the thumb and forefinger of each hand. Dekan, "Finding out Its source of power, learning all Its secrets. Subjugating It. Bending It to our Human will. Forcing It to confess. And finally - smashing It! So we finally get our own back for all the misery It's caused us. Then, when It's been disposed of, we humans will take over the Universe. And run things properly." In light of Mike's sacks of grain vs cuniform distinction, its probably good to remember that you can hold the counters in your hand, but you can not actually grasp the universe. Your hand is not big enough. Regards, TAR

Strange, I will go with immensely complex. Its evident. Then perhaps the point is, that science is misguided when attempting to simplify, when it is the complexity that makes the place. Perhaps it is a double edged sword that science attempts to wield. Find the patterns, but find the many patterns. Simplification, as suggested in the thread title is not then the "goal". It is important to discover and push the boundries and limits of current technology to give others in the present, and those in the future, the tools and abilities to see farther and smaller, sense and record the tiny and the immense and hone the understanding of the rules by which it is apparent that the word operates in accordance to.. But there may be a misguided suggestion embedded in the OP. That there is an "insight", a simplification, that should and will bring everything into focus, that is currently blurry or out of sight. Some one equation that ties together GR and SR or that can predict the emergence of life. Some "final" goal. I suppose that is not in the cards. Everything we find out, every onion peel we remove, reveals on the one hand the underlying aspects of the previous peel, but reveals a new and different core to wonder about. It is unlikely, given the immensity of the place, that we will ever run out of universe to explore. It is also evident that we are already able to bring the universe into focus. By opening our eyes, and our imaginations, to its wonders. Regards, TAR

So, Strange, Is it possible that the epicycle type of complication proposed by the OP is occuring now, and the more and more complex math required to explain things, an indication that a simplifying insight is in order, to maintain science's tack toward clarification and explaination, and away from complication and obstification. I believe you are right, that it is sad that science can not explain itself so clearly to the layman as it once could, but while maintaining a healthy adoration for the work that has been done, and the beauty of peer review and reproducable experiments and all, it is my opinion that a certain amount of skeptism is healthy and allowed. Its OK to have a speculation section where old folks like Mike and I can raise some questions and make some general statements, and question accepted mainstream science a little, without harming the process in our woolyness, or lack of rigor. Neither of us is suggesting that things that are true are false. In fact, in PMs we have agreed that one important principle is that what is true, will remain true no matter what we say about it, or think about it. We just like things to add up, and make sense in more than one way, like every other scientist. And both Mike and I are on the last third of our lives, and would like to contribute something, if we can, to humanity. I do not think we are hurting the process of scientific progress with our insights and questions and opinions and observations. Maybe we are, but whatever progress science makes is only useful progress if most of the population of the Earth sees it as progress. Whether complex or simple its application to every man and woman's life is important. If it is too esoteric, and makes no sense, it is of questionable value. For instance, of what value is the fact that universe is 97 percent made up of stuff we will never interact with. Is it not more prudent, scientifically speaking to concentrate on the stuff we do and will interact with? In this, the equation itself seems to me to have taken on more importance than the stuff the equations are supposed to be helping us grasp and use and notice and enjoy. A little philosophy is good to mix in with the numbers, so that the meaning behind the numbers can be grasped and shared by everybody, and then science can remain the endeavor of the human race, and not the special pervue of an elite few, who "understand the math". Regards, TAR

OK thread, This is getting really neat. I redrew the 2D Sedge layout and cut it out, and it of course made a tetrahedron when you fold it on the three internal lines. (Upside down and backward from the layout on a sphere, but otherwise perfectly related.) But then I cut out the shield shapes and found I could rearrange them, taking one whose outside edge touched the outside edge of a distant shield in the same association as found on the numbered diamond sphere, and I continued to do it, and it made this nice equilateral triangle. Who knew that the surface of the sphere was in the shape of a triangle! Measured my pieced together triangle a few times and averaged out the base to 320 and the height to 279. This multiplied out to 44640. using 118 as the diameter and figuring the surface area of the sphere, I got 43743. These are .98 and 1.02 of each other. Pretty close. As if perhaps pi might be found within the proportions of an equilateral triangle. And within the proportions of a spherical rhombic dodecahedron's diamond.

But back to the Spherical Rhombic Dodecahedron and how to transfer it to a 2d surface. Create the 12 sections of the tetrahedron and each SRD section correlates exactly to one section of the tetrahedron. Using the Sedge (three tetrahedron edges rounded) the transfer of the tetrahedron faces to a 2d (four triangle) shape becomes evident. Of course everything is backward and upside down, and the choice of where to start (which diamond in what orientation in what position is to correspond with what position on the sphere) is arbitrary. But once you start, every other position transform from the sphere to the 2d surface is exactly determined. (provided the grid system is drawn on both the sphere and the 2d surface, on the diamonds (and shields) shown. Sphere Area= 4pi r squared = 4 pi 59 squared = 43,744 (using crude measuring with the 1/60th of an inch unit, and an approximately 1 inch diameter sphere) (actual square degrees in a sphere 41,250. Triangle Area = 1/2 base times height. The triangles shown measured all over the map, so better precision is definitely possible, but going by a base of 145 and a height of 140, with 4 of them, it comes to 40,600. Close enough to imagine a 1 to one correspondence between a division of a diamond on the sphere and a division of a shield on the 2d diagram. The boundry lines between the diamonds on the sphere are all 1r. The boundry lines on the tetrahedrons are different, with a different length touching three points than touching 4 points, but it looks regular and forgiving. Would be interesting to see what a globe would look like projected onto this. Or twelve photos taken in twelve directions and pasted on the tetrahedron or the 2d scheme...lots of thoughts.

Attempt one not shown. Attempt 2 and three shown twice, repositioning the figures between shots. These are divisions into 8 sections and not directly related to the thread (perhaps, but I have not seen the connection.) Its (the eight) is two square planes on top of each other, rotated 45 degrees from each other. Have not "seen" if that builds out to the same matrix behind the spherical rhombic dodecahedron. (talking about attempt 3 with the eight large diamonds, four touching at the North and four at the south) I think the eight start a different matrix. the square planes in the 12 have each ball touching 4 balls in the next plane, where here it looks like two here. Sorry, those are lousy and confusing pictures. Each of the two balls is showing something different. The one with the toothpicks is the eight diamonds with a pick at the North pole, the south, four equal distance from each other in the Northern Hemisphere, and four in the South. They form the vertices of the diamonds. Two four points at the poles and eight three points, four each equal distance from the respective poles and spun around the axis of the poles 45 degrees from each other. The other ball is eight tangerine slices, but four form a hemisphere as do the other four, but the one hemisphere is spun 90 degrees to illustrate how the great circles are imaginarily cut in quarters, so that one can say the unseen vertex is there, cutting the one semi great circle into two "sides" of the diamond (the 180 degree angles of the elongated diamonds with the 45 degree angles being at opposite podal points.) Confusing the picture even more is the fact that of the eight tangerine sections I drew a grid in two of them to indicate the opposite nature of the "sides" of the diamonds.

Actually my figure worked except the sides might not have been on great circles. When I forced them onto great circles I got a tangerine section set up so the "diamonds" had four points, two with internal angles of 45 degrees and 2 at 180 degrees (two sides on a great circle and the other two sides on another great circle. So you might disallow both those attempts, but then on a third I found you could simply make four diamonds touching at the North Pole and 4 touching at the South pole, the bottom tip of the North ones being way in the southern hemisphere and vice a versa.

Strange, OK, yeah I see what you mean. General statements, like the kind Mike and I often make, are more Philosophical than particular and rigorous as a scientific statement would be. In regards to this thread though, the progress toward simplicity would be toward the general statement and away from the ecsoteric details of the particular mathematical model. Here general statements, fittingly describing the nature of the world are perhaps the goal. Regards, TAR

Commander, "Strangely, there is no way of producing 8 equal Square faces on the Sphere, Using 2 tetrahedrons in a mirror tilt may produce 8 equidistant points on the surface of the Sphere but connecting them may again result in Triangular shapes and not squares." I took this as a challenge and was thinking this morning about it. I think I succeeded in making such an "Impossible" division of the sphere into 8 four sided figures, with all four sides being the same length, and on the surface of the sphere, and I believe each line is on a great circle. I will make it again and take pictures of it, tonight. TAR

Moment Theory, Good point. We already, as universe material did the singularity thing. Now we are doing something else. I tend to think, philosophically that the universe does everything it does, when it does it, for the first time. That is, that prophecy is not a very sensible suggestion. If we already did the thing, we could not just now be doing it for the first time. Certainly we can predict outcomes when certain things combine in a way that has before resulted in certain outcomes, but it would be difficult, for instance, for Newton to predict the Apple itune store. Too many new things developed inbetween when Newton Lived and 1972 when the microprocessor came into existence. And too many things happened for the first time, since 1972. And to your point, we are very well insulated by time and space from the Big Bang singularity. It is very far in our past, and will be a very long time until we return to such a state. It should not be held as either a source or a destination, in any meaningful way. We are too far from it, for it to be a significant factor. Regards. TAR

SwansonT and Strange, I apologize, my post was obviously a non-sequitur as you suggested, and I did not properly understand Strange's intent, to boot. I was mostly after backing Mike Smith Cosmos, as his contributions to this board and the inspiration I take from here are important and substantial to me, and I don't agree with you Strange, when you suggest that Mike is not a man of science, and that somehow you know what science is, and Mike does not. I suppose I take some personal offense when Mike is attacked for being unscientific, because I am a laymen compared to Mike, and I like to think I know enough to be on this board. So. to explain the non-sequitur a little, I am myself on a quest to understand what Pi is, or why Pi is (I already know its the ratio of the circumference of a circle to its Diameter,) So I made a side connection between Euler and my investigation of the spherical rhombic dodecahedron. And if there is something to be learned about the world, by understanding its geometry, then Mike and I, in our investigations of orthogonality and intersecting hexagonal planes, might actually be making some progress, along the lines of the progress that scientists tend to make, in understanding the world and its rules, and how it fits together. I am sorry for reacting the way I did and misrepresenting your intent, Strange, but this is my world too, and I am not an idiot, nor ignorant of Science, nor unthankful for the benefits to humanity that the scientific method has bestowed. It is not up to you to decide what is science and what is not. Regards, TAR

SwansonT, Sure you can get a BA or a BS and the two degrees are distinquishable from each other, but Strange was implying you cannot get anywhere with art, and that you can get somewhere with science. I was attempting to point out, that the two are different aspects of the same human endeavor, and if Science is a process of continual simplification as is the title of the thread, then "the goal" would be reached and the process would be complete as soon as E=MC squared is written. Since this does not seem to be the case, the unification of the forces and the tieing together of GR and SR into a "simple" pattern and formula, would NOT be the end of it. The universe would remain as huge, complex and longlived as it is, and the imagination of the Scientist would NOT trump the imagination of the Artist. Regards, TAR P.S. I only picked this thread up after the split. And was taking it for what it was as is, with no earlier thoughts related to creationist thinking involved. If my post was a non-sequitur to earlier thoughts I apologize, but I did not read the earlier thread.

Commander, Post 70 in this thread shows my version of your roofed cube. The divisions are the same in terms of internal angles (90 at the 4 points and 120 at the three points.) Except to retain the 12 divisions you ignore the edges of the cube, and count half a diamond as your 1/4 roof on one side, and combine that with its neighboring 1/4 roof on the touching side. I will have to accept your statement that you can not make 8 equal diamonds. Seems the 12 sections work out so nicely to divide the tetrahedron, the octahedron, the cube and the sphere, it would be unlikely to suspect that another number, other than 12 would work as well. I had not been able to see the relationship of the cube octahedron I started with, to the dodecahedron with the pentagonal sides. Perhaps now that using 10 out of the twelve tetraheral sections to make that five sided figure a few posts ago, there might be a relationship, after all. However, the spherical rhombic dodecahedron, is still the better of two dodecahedrons, as far as I am concerned. It has the cube, octahedron and tetrahedron built in. It has the 4 intersecting hexagonal planes. It has the 3 intersecting square planes. The diamonds can be divided in a grid pattern, seemingly proportionally around the hexagonal planes, into degrees, minutes, seconds and fractions of seconds, which you can not do with the pentagonal dodecahedron. If you imagine a ball at the center of the figure, 12 balls of the same diameter will fit exactly around the center one, if placed exactly in the middle of each of the 12 diamonds. This pattern of hexagonal and square planes, that is thusly indicated, can be extended outward indefinitely. Each of the sides of the diamonds appears to be exactly one radius of the sphere that the spherical rhombic dodecahedron is drawn onto. Any one of the said 12 sections of the sphere can replace any one of the 12 sections of the cube, the octahedron and the tetrahedron, in terms of the sections' internal angles. Because of this, mapping the surface of any of the shapes to the other could be done, in terms of the designations of position on the sphere according to the hexagonal plane 360 degree grid model shown earlier. Regards, TAR

Strange, "Art is not science and never can be". What aspect of Art has no science as a part of it? What I mean, is that the universe is not divided into an Art section and a Science section, that have nothing what so ever to do with each other. There is the Occum razor situation, in regards to this thread that indicates that simpler is better. E=MC squared is rather simple a statement, yet from it, emerges the complexities of the universe. Not that the equation made the universe, but the model, provided by the equation, is representative of the actual universe in the universe"s adherence to the simple relationship expressed in the equation. I have been working with clay balls, drawing dots and lines on them and cutting them up. More art than science. Simple, direct fitting of pattern to actual space and geometry. Not too much math involved. No sines or cosines, just pi and measurements and multiplication and angle measurements. More art than science, but the relationships I am discovering are real and fit reality nicely. The complexity of the equations that figure volumes and such adding up matrix elements and taking the square root of a bunch of terms and dividing that by quotients of other items is complex. Cutting a piece of clay up and experimenting with the angles and relationships, is simple. Simple, but real and fitting in terms of the universe. Art is thus real science, in the sense that the imagination is guided by the possible forms and shapes and interactions of reality. You can not paint blue in a picture, unless you have pigment that absorbs the other wavelengths of light, other than blue, or unless you have a computer pixels that put off the right wavelengths. If you think science is only the understanding of the complex equations required to figure a simple angle or shape, I think you might have the whole operation backward. The complexity of the model of the simple thing is not better than the simple thing. Then, on the other hand, science attempts to express the activity of the universe, including all the complex emerging entities within, in terms of simple equations, like the gas law. This attempt is more imaginary in nature, than actually fitting and proper in describing reality, so this type of scientific venture would in some ways be more Art, than science. Bottom line, the act of being a human, involves to a large extent the internalization of the outside world, the building of an analog model of the place within the synapses and arrangements in the brain, and working with the model, to construct a next action or non action that will be beneficial to survival and will result in the avoidance of pain and in the achieving of some pleasure. There therefore has to be some art in science and some science in art. They are not separate things. Regards, TAR

somehow the sections wind up with that 36 degree angle. Two make 72 degrees, 5 make 180 and 10 make 360.

Thread, Cut up a 1/4 pound clay tetrahedron into the 12 sections and replaced one Sedge section with one Tetrahedron section and vise-a-versa. Show the twelve sections. Then the surprise. I put the sections outside face to outside face to see how they would pack, and got six peices that unexpectedly fit together as shown. 10 of the pieces completed a circular pattern with a flat side. The other two pieces made the 6th piece which fit nicely upside down in any one of the five "places" for it. Seems the sections will pack nicely. Regards, TAR

Thread, Was cutting a Sedge into its 12 sections. Just got the first section cut out and realized they were not going to all be identical. Then I thought that was because some edges of a Sedge section were cut from the edge and some from the face. Then I realized I could not have that issue if I never rounded the three edges required to make the Sedge in the first place... Don't remember if I ever made the 12 sections of the tetrahedron. If not, I will soon and post them. Seems those twelve sections should be very interesting with interesting properties. Might even be a way to pack space with them. Just a waking thought. Will pursue it later. Regards, TAR

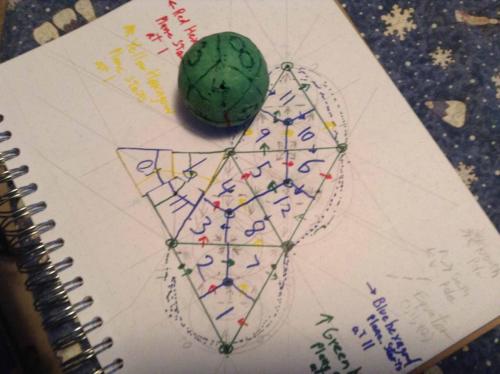
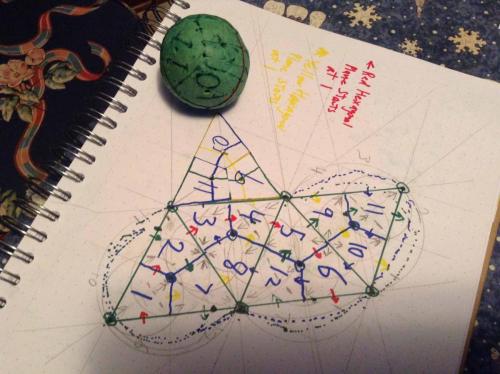
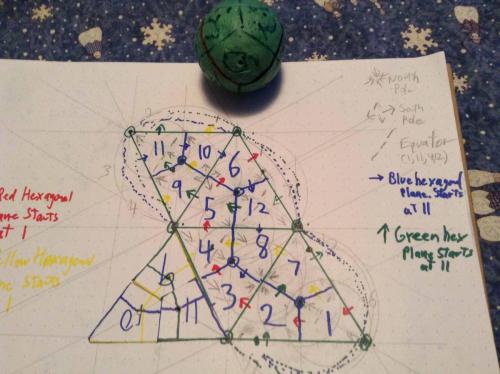
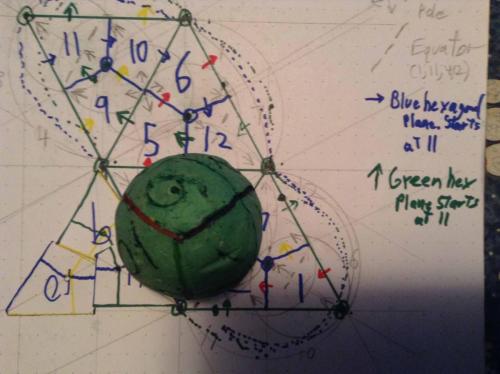
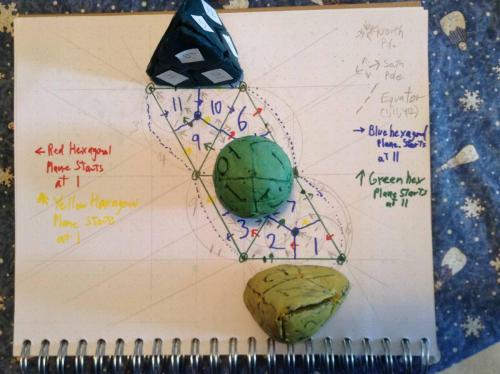
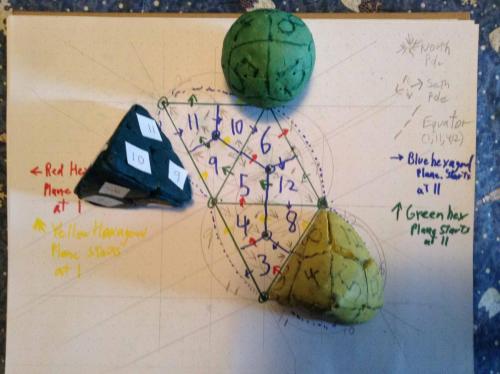
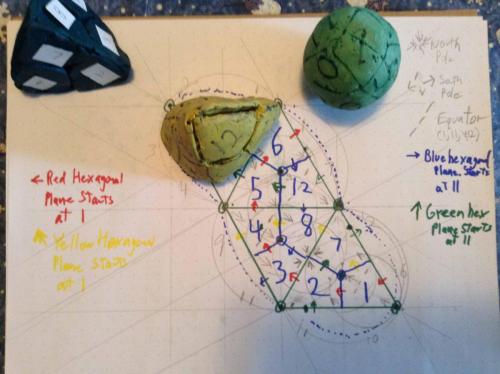
Thread, While cutting the diamonds off the surface of a sphere I accidently came up with a 1 faced, 1 edged, 2 verticed figure that I started a thread on, and continued to investigate. I can make it at will now (based on a tetrahedron,) and it has a definite relationship to the twelve sections of the sphere. There are left handed and right handed versions of the thing, and you can "start" the thing on any of the twelve sections, in each of the four orientations possible. The numbering scheme I suggested earlier can be readily applied to this figure, and the imprint of this figure on a 2D surface. The Red hexagonal plane describes a nice semicircular arc (open to the NW) (1,6,5,4,3,2) The Blue hexagonal plane describes a nice semicircular arc (open to the SE) (11,3,8,12,6,10) The Yellow hexagonal plane describes an S to the left and down (1,7,8,4,9,10) And the Green hexagonal plane describes a S tilted to the right and up (11,9,5,12,7,2) Regards, TAR (copyright TAResolutions LLC) (sorry my NW and SE, up and to the right is all 90 degrees off, I took the picture after rotating the book 90 degrees CW)

So, Bottom line, this figure is not so very odd, unique or surprising as I initially thought. But its still interesting, as each point on the face has its unique position on the surface of the sphere, thus allowing one to consider projections from two to three or three to two. And it probably therefore has something to do with a sphere, especially since it shares the property of having one face, and since it has the circle built in. Regards, TAR But, As my wife pointed out when I showed her the version I crudely made from the tetrahedron. "It's not as pretty as the original one". The first (the one pictured,) was neat to hold in your hand and turn and feel and look at. Very balanced, the lines where/are very satisfying. Sort of a 3D yin yang. I'll still call it the Sedge. Regards, TAR Well, Got it figured, It is definitely neat. And does go along with the twelve sections of the Sphere, Cube, Tetraherdron, Octahedron. Same internal angles, same 12 diamonds. I give you the 12 divisions of the Sedge. Regards, TAR Wow! Just found that a sphere made from 1/4lb of clay and marked out with the diamonds, rolls out (what appears like might be) exactly on the Sedge imprint, made with a Sedge, made from a quarter pound of clay. Might be even more interesting a figure than I originally sensed. Let me clean up the middle of that last diagram and try things out a bit. Wierd, but this might even be a basis for laying out small distortion 3D images on 2D surfaces. (360 degree images, at that.) Regards, TAR By the way, I claim copyright on the images of the Sedge, and the shape it rolls out on, included in this thread. (Not Commander's of course, that is his.)

Ok, Forget the left right left right stuff. It looks like its related to the three diamond sections, but although I have not nailed it down completely, I believe you start cutting pretty agressively under two diamonds, possibly starting at a four point, and work your way around a three point to your right until there is not a surface diamond left to your right, at which point you turn left and take the diamonds left on the surface. Or it might be the same idea but working your way around a four point. In any case, I think I have the basic idea down, and I just have to reproduce the thing, to tell you exactly how its done. All I know is its possible, because I have the figure right here, and it absolutely has only one face and one edge that terminates at each end. although I just made something like it, without marking any diamonds on the sphere at all seems its just what you get if you start cutting the peel off around a point and then switch directions around a point on your left to complete the peel The only help the diamonds might give is to provide the width of the peel that will make the thing just exactly symetrical. Actually the figure does not have that much to do with even the sphere, except for possibility of projecting a sphere unto that two dimensional shape it rolls out onto. I just made something with the same properties by starting with a tetrahedron, and marking three of the edges (in like an S) for edge duty and the other three for destruction (rounding off,) Then its just a matter of pushing the clay around until its in the same shape as pictured above.

Commander. Perhaps the semicicular remark was misleading. It might not be a semicircle, might be a third of a circle, for instance, But perhaps, since the shape works, it has to be a semicircle. The first of your three drawiings is the closest to the situation though. Your reference to the two semicircular faces, was incorrect. The two "semicircles" are on the opposite ends of the same face, in such as to cause the bottom of the cone to roll out while the apex is stationary for half the trip along the face, and cause then the apex to be stationary on the near side, while the edge rolls out on the other side. Not well described, but I have to get ready for work. Later. Regards, TAR remember that the "semicircles: are the edge and there is only one edge Commander, OK, couple more hints. When I started I cut shallow great circle lines at the North Pole four point and the South pole to allow the surface to move and open up as I made my normal to the center type cuts to remove the surface diamonds. My depth of cut was such as to just get under a complete pair of diamonds. This is an interesting statement, but in the other thread, somebody pointed out that the four points of the diamond are not all on the same plane and whatever my rule was, to pass as close beneath the diamonds as possible,without breaking the surface, somehow picked a path of cut that respected all four sides of a diamond at once. Another hint, as to the path I may have taken is that one can get around a sphere laid out in the spherical rhombic dodecahedron pattern in four diameter length moves along the surface. Start at a four point, travel one radii along the sides of touching diamonds, take a 120 degree left, travel 2 radii, take a 120 degree right, travel 2 radii, take a 120 degree left, travel 2 radii, take a right and travel 1 radii back to your starting point. I have not done this yet, cutting below the diamonds, but I traced it out on the sphere, and it does account for all 12 diamonds and may be the path I took to cut the surface off and be left with the sedge. Regards, TAR

I will have to get back with you, on this. I can not figure out how I did it. My markings were obscured, so I am not sure what lines I followed or why. It was sort of accidental. I will have to continue to try and reconstruct the situation. By the way, just put six spheres around a center ball and three on top and then three on the bottom diametricallly opposing the three on the top. Nice close packed situation with 4 intersecting hexagonal planes and three intersecting square planes, is seeded and can extend out indefinitely as Janus rendered in the other thread. Balls in such an arrangement are at the centers of the diamonds, spacing wise, as the diamonds are drawn by placing a line exactly between each ball and the closest other four.

Commander, I had the same thought. Matter of fact, I still have the clay piece I cut off, from around the figure, with the spherical rhombic dodecahedral markings on it. I will fix it ( piece got cut and fell off) and take a picture of it, tonight. Since it is one piece, and the figure has one face, there is probably a one to one correspondence between the demarkations on the outside of the sphere, and the points on the 2d surface of the singular face of the figure offered in this thread. A lot of possibilities for the projection of spherical surface characteristics onto the two dimensional space that I rolled the face along, above. Interesting, because once I see where I made my cuts and such I can draw out the twelve sections onto the above 3d figure's face, as well as onto that s shaped 2d figure with the circular ends. All sorts of applications might come from that. I will retain rights to having come up with the system though, if it turns out to be as useful as its appearing to me at the moment. Your discovery however was/is coincidental so I suppose you are a co-discoverer, should this be a new discovery. As I would like to call the 1/12 solid section of the sphere, the Janus, should it not yet have a name, I would like to call the figure depicted in this thread, the Sedge, after the S shaped edge, (and a co-worker I talk about this stuff with,) should it not already have a name. Regards, TAR It is, after all however a geometrical shape, which belongs to everybody, so only its applications to 3D graphics, photography and printing, 3 dimensional coordinate systems, and projections and such would be things carrying any ownership rights. I will retain any such rights due to me, while giving due credit and ownership to those on this thread and the 12 section thread that have assisted in the development the associated ideas, models and diagrams. By the way, it appears that you should be able to start your cut at any of twelve identical spots on the spherical rhombic dodecahedron, and come up with the same figure. Being that the figure is mirror image of itself, that might mean you could get 6 different cuts off the surface of the sphere, depending on where you started (where you end, meaning the same thing as if you started there.)