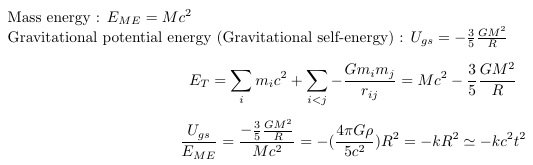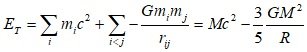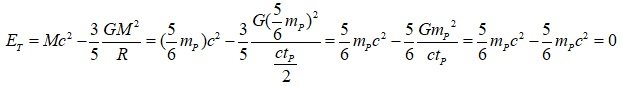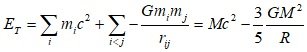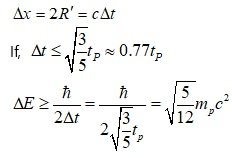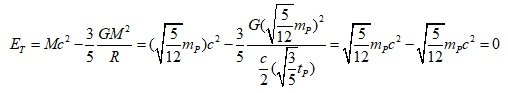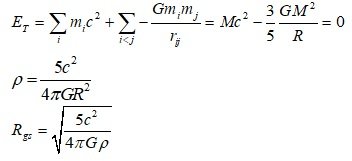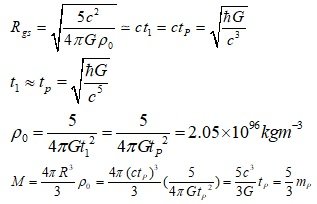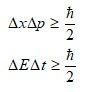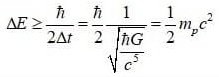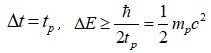-
Posts
116 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by icarus2
-
In the shell theorem, the force inside the sphere is 0. However, the gravitational potential energy inside the sphere is not 0. Therefore, the sum of the gravitational potential energies created by each sphere is not 0, and exists. That is the gravitational self-energy equation. The universe is a negative mass state, so it is a universe dominated by repulsion, not attraction. Therefore, it does not collapse due to self-gravity. In the early days of the universe, I showed that E_T can be 0. I also explained that E_T can be in a negative energy state less than 0. Since I proved Zero Energy, it is easy to infer that it creates a negative mass state. Let's assume that 10 Planck masses are created during the Planck time. It becomes a state of negative mass and negative energy. Since there is a repulsive gravitational effect between negative masses, the universe cannot contract but expands. Therefore, the universe exists without collapsing, and it can explain the accelerated expansion of the early universe. Even though a single quantum fluctuation is set to 0, as time passes, the surrounding quantum fluctuations participate in gravitational interactions, so the negative gravitational potential energy increases faster than the positive mass energy, so it can explain that the total energy of the system becomes a state of negative energy and expands. The above mechanism explains the mechanism of the early universe expanding without collapsing. Now, let's look at the current observable universe. If we calculate the gravitational potential energy of the current observable universe, we get a value of approximately -3.04 times the mass energy. The current gravitational potential energy of the universe is approximately 2.04 times greater than the mass energy. Therefore, the current universe is also in a negative mass state, and therefore, the universe does not collapse. This is also consistent with the hidden result of standard cosmology. Why doesn't the universe collapse? The universe is in a state of negative energy, so it didn't collapse because anti-gravity is stronger than gravity~ Are you not reading my writing? I have proven the value of dark energy density through my model, and In a rough estimate without correction factor, the cosmological constant value by the gravitational potential energy model is 2.45x10^-52m^-2, which is very close to the observed value. While the value of dark energy was proven through the gravitational potential energy model, this paper introduces quantum fluctuations, and one may wonder whether this also creates a vacuum catastrophe problem. Here are some points that are different from the mainstream vacuum catastrophe problem occurrence and my personal opinion. 1) I am negative about applying zero point energy derived from simple harmonic oscillation to the universe. In the SHO model of quantum mechanics, there is a potential V with a negative value, and the width of the well also exists as a function of the potential V, so in this case, zero point oscillation will exist, but I think there is no basis for the existence of a potential V with a negative value in the universe and for limiting the width of the well to the Planck length. Since the vacuum of the universe is likely to have similar energy values, I think there is a problem with assuming that there is a potential V with a negative value and that it will exist at every Planck length, as the mainstream estimates. 2) In the mainstream vacuum catastrophe problem, the mainstream does not consider gravitational potential energy, that is, gravitational self-energy at all, so the vacuum has an enormous energy density and this becomes a problem. However, in my model, even in the case of quantum fluctuations, there is a gravitational source ΔE and a time Δt for gravity to act, so I have said several times that gravitational self-energy should be considered. And, considering the gravitational self-energy, we proved that near t=t_P, the total energy, including the gravitational potential energy, and the total mass can take the value 0. That is, I showed that the energy density of the vacuum can be 0 or close to 0. Here is one possibility. If, Δt=t_p, ΔE=(5/6)m_P, (5/6)m_P is near m_P. 3) In the previous article 3.6(3.6. The Vacuum Catastrophe Problem or Cosmological Constant Problem), when the mainstream claims that the vacuum energy density exists, we calculated the size of the event horizon formed by the vacuum energy density. The event horizon created by the vacuum energy density within a radius R=l_P/2 is R_S=2.09 l_P, which is larger than the radius R of the mass or energy distribution, so the vacuum energy is trapped in the event horizon formed by its own mass, and therefore, it cannot exert a force on the outside and has the possibility of disappearing. 4) There may be an unknown reason that we have not found. In the case of the gravitational potential energy model, the mass M inside the shell is not a constant but a variable, and it is difficult to solve the problem because it includes M(t) --> M_(t) + ( -M_gp(t)). After thinking about it for a while, it seems that the total energy inside the shell is not conserved, and it seems difficult to derive the first Friedmann equation using the mechanical energy conservation equation. To derive this, we need a genius who can take a new path, not someone who follows the examples pioneered by others. If there is anyone among the readers who has the ability, please try to derive it. So, until a genius who can build such a new model appears, if we apply a temporary method, we can think of the following method. Both the existing Friedmann 1 and 2 equations include the same dark energy term (1/3)Λc^2. Therefore, we can put the dark energy term obtained from the second Friedmann equation into the first Friedmann equation as it is. I derived the dark energy term from the second Friedmann equation, and the dark energy value calculated using the derived dark energy term is very close to the observed value, and by adding a correction factor, we can make it match completely. Therefore, Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field
-
E_T = Mc^2 - (3/5)(GM^2/R) is not an equation used to describe the conservation of mechanical energy in an expanding universe. It is an equation close to rest mass energy. M can also be expressed as M_rel. The rest mass of an object is the total energy including the rest mass, kinetic energy, and potential energy (gravitational self-energy, electromagnetic self-energy, and potential energy related to the strong and weak forces) of the particles that make up the object, divided by c^2. In other words, the rest mass of an object includes not only the rest mass of the elements that make up the object, but also the potential energy between the elements that make up the object. Representative potential energies include gravitational potential energy and electrostatic potential energy. This can also be understood through the following figure. M is the combined state of dMs. Therefore, it has potential energy. If there is an object (mass or energy distribution) as above, let's divide this object in half virtually. Then, the left hemisphere A and the right hemisphere B will exist, and the centers of mass of the two hemispheres will exist. The centers of mass of the two hemispheres are separated by a distance r, and this r is not 0. Then, according to the definition of gravitational potential energy, in the equation U=-G(m_A)(m_B)/r, m_A(mass of hemisphere A), m_B(mass of hemisphere B) exist, and the distance r also exists between the two centers of mass. Therefore, gravitational potential energy U exists by itself. Since the differential concept of dividing all objects into the masses of the infinitesimals that compose them is established, gravitational potential energy exists between the infinitesimals that compose the objects. Therefore, in any entity or any energy distribution, we must consider gravitational self-energy(or - gravitational binding energy) and electrostatic self-energy when calculating the total energy. However, if we do not assume the existence of charge (if we simply define the energy distribution), we can exclude the electrostatic self-energy term. Also, since electrostatic self-energy is positive energy, it can be included in the equivalent mass M of positive energy. As a result, if we assume an entity with some energy that has a spherical uniform distribution, the total energy of the entity can be expressed as E_T=Mc^2 - (3/5)(GM^2/R). Strictly speaking, M is the total energy when the particles that make up the entity are in a free state. However, in most situations, the gravitational self-energy is small compared to the mass energy, so M_free ~ M_0 holds. 1) Mass energy and gravitational self-energy in the case of a proton Proton mass = 1.67x10^-27kg Proton radius = 0.84x10^-15m For example, in the case of a proton, the gravitational self-energy is very small compared to the mass energy, at the level of 10^-39. 2) Mass energy and gravitational self-energy in the case of the Earth In the case of the Earth, the gravitational self-energy of the Earth is also very small compared to the mass energy, at the level of 10^-10. Therefore, we have not considered this gravitational self-energy (the gravitational potential energy that the mass distribution of the object itself has) in most problems, and have forgotten its value. As can be seen from the calculation above, the negative gravitational self-energy is not always equal to the mass energy. However, there are situations where this gravitational self-energy becomes very important, and these situations are presumed to be the source of important problems in current physics and astronomy. 1) Black hole singularity problem 2) Dark matter and dark energy 3) Inflation mechanism 4) Birth of the universe from quantum fluctuations ... ========== Now, let's look at the birth process of a single quantum fluctuation covered in this paper. Let's assume that a single quantum fluctuation is born with the size of the Earth and the mass energy of the Earth. The energy ΔE=(M_E)c^2 remains, and therefore, it has a very short Δt. Therefore, it is difficult to explain the birth of the universe from nothing (zero energy) and its existence to the present. Let's assume that it was born with the size of a proton and the mass energy of a proton. The energy of ΔE=(m_p)c^2 remains, and therefore, it has a very short Δt. Therefore, it is difficult to explain the birth of the universe from nothing (zero energy) and its existence to the present. In both cases, ΔE=(M_E)c^2 and ΔE=(m_p)c^2 remain, and it is difficult to explain the birth from nothing. However, let's assume the following situation calculated in this study. 1)If, Δt=t_p, ΔE=(5/6)(m_p)c^2, 2)If, Δt=(3/5)^(1/2)t_P, ΔE=(5/12)^(1/2)(m_p)c^2, The total energy of the system is 0. In other words, a mechanism that generates enormous mass (or energy) while maintaining a Zero Energy State is possible. If ΔE_T --> 0, Δt --> ∞ Δt where quantum fluctuations exist can be very large. In other words, Δt can be larger than the current age of the universe, and these quantum fluctuations can exist longer than the age of the universe. In addition, by the 2nd mechanism, since the negative gravitational potential energy exceeds the positive mass energy, the corresponding energy distribution has the characteristics of negative mass, and through this, it can explain the accelerated expansion of the early universe(Inflation) and the accelerated expansion of the current universe(Dark energy).
-
The gravitational self-energy (or gravitational binding energy) equation is in most classical mechanics books, so there is no need to derive it separately. https://en.wikipedia.org/wiki/Gravitational_binding_energy The article you linked to is a mainstream model, and is different from my model. That model omits the gravitational self-energy that M itself has. In the following article, I will roughly explain the acceleration equation according to my model. People generally react that way when they encounter something different from their existing paradigm. One such object is “negative mass.” But don’t worry! There is a word prepared for such people. Equivalent, Effective Please think of it as negative equivalent mass, effective negative mass, not negative mass. In this model, particles, stars, and galaxies all have positive mass and positive energy. These positive masses create gravitational potential energy with a negative value. Therefore, the system, including the potential energy, can reach a negative energy state. However, the average density of negative gravitational potential energy is very low. Therefore, individual particles, stars, and galaxies are still in a state of positive mass. The universe (system) that includes them all is in a state of negative energy, and therefore, only the observable universe has a state of negative equivalent mass. Since individual particles and galaxies are still in a positive mass state, so if you're overreacting to the term "negative mass," please feel safe. ------------ Based on the gravitational potential energy model, the acceleration equation is derived as follows: The Friedmann equation can be obtained from the field equation. The basic form can also be obtained through Newtonian mechanics. If the object to be analyzed has spherical symmetry, from the second Newton’s law, R(t) = a(t)R By adding pressure, we can create an acceleration equation. Let’s look at the origin of mass density ρ here! What does ρ come from? It comes from the total mass M inside the shell. The universe is a combined state because it contains various matter, radiation, and energy. Therefore, the total mass m^* including the binding energy must be entered, not the mass “2m” in the free state.“m^∗ = 2m + (−m_gp)”, i.e. gravitational potential energy must be considered. We may need to correct the value for some reason, so let's calculate it by inserting the correction factor β(t). −ρ_gp is the equivalent mass density of gravitational potential energy, Instead of mass density ρ, we have (ρ) + (ρ_gp). So, Dark energy term and Cosmological constant term is *There is no cosmological constant in the gravitational potential energy model. However, since the existing standard model was built based on the cosmological constant model, it is expressed in the form of a cosmological constant term for comparison. If we obtain the cosmological constant and dark energy terms through this model, Please look at the case when there was no correction factor at all, that is, the pure predicted value. β=1 You can see that it is almost identical to the current cosmological constant and dark energy density. In other words, the gravitational potential energy model is 10^120 times more accurate than the vacuum energy model! (It is close to the dark energy density value.) In addition, since it shows that the dark energy density is a function of time, it is different from the ΛCDM model and can be verified. The current standard cosmology is the ΛCDM model. This model explains the dark energy problem by introducing a entity that has positive energy density and exerts negative pressure. However, cracks in this ΛCDM model have been increasing recently, and accordingly, the time is approaching when other possibilities and interpretations should be seriously examined. The ΛCDM model consists of Λ(Lambda) and CDM(Cold Dark Matter), but it has not succeeded in explaining the source of Λ, which is the core, and the vacuum energy, which was a strong candidate, has an unprecedented error of 10^120 between the theoretical value and the observed value. CDM has also not been discovered despite continued experiments. In addition, particle accelerator experiments, which are a completely different approach from WIMP detectors, have not found a candidate for CDM. Furthermore, the existence of the Hubble tension problem has recently become clear, and in January 2024, the DES (Dark Energy Survey) team raised the possibility that the cosmological constant model may be wrong, and in April 2024, the DESI (Dark Energy Spectroscopic Instrument) team announced results suggesting that the cosmological constant model may be wrong. Since it is only the first year of results, we will have to wait a little longer for the final results. 1)Dark Energy Survey team https://noirlab.edu/public/news/noirlab2401/?lang 2)Dark Energy Spectroscopic Instrument team https://arstechnica.com/science/2024/04/dark-energy-might-not-be-constant-after-all/#gsc.tab=0 The gravitational potential energy model creates a repulsive force on a cosmic scale, and it also explains the dark energy density value, so people better than me need to study this model more seriously. Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field
-
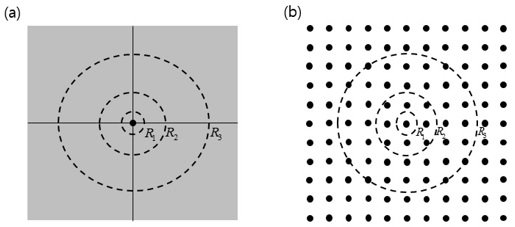
As I explained before, in our time, when using the expression of rest mass, the expression “m_0” was mostly used. This is the notation of Marion, a representative classical mechanics book, and also the notation of Beiser’s book, which is used as a modern physics textbook. It also appears in the expression you wrote. And, you can see it in my previous paper. https://www.researchgate.net/publication/263468413_Is_the_State_of_Low_Energy_Stable_Negative_Energy_Dark_Energy_and_Dark_Matter Mc^2 is the total energy of objects with positive energy, and M is the relativistic mass or equivalent mass. As I explained before, I do not think that the total energy of the universe is zero energy. I claim that the total energy of the observable universe is in a negative energy state. I claim that the universe is experiencing accelerated expansion because the negative energy of the observable universe is greater than the positive energy. I also think that this is the hidden truth behind standard cosmology, and that the mainstream is missing it because of their preconceptions about “negative mass”. 1.The first result of Friedmann equation for accelerated expansion was negative mass density Nobel lecture by Adam Riess : The official website of the Nobel Prize Refer to time 11m : 35s ~ https://www.nobelprize.org/mediaplayer/?id=1729 ===== Negative Mass? Actually the first indication of the discovery! *This is a phrase that appears on Adam Riess' presentation screen. ===== HSS(The High-z Supernova Search) team : if Λ=0, Ω_m = - 0.38(±0.22) : negative mass density SCP(Supernova Cosmology Project) team : if Λ=0, Ω_m = - 0.4(±0.1) : negative mass density *This value is included in a paper awarded the Nobel Prize for the discovery of the accelerated expansion of the universe. In the acceleration equation, (c=1) (1/R)(d^2R/dt^2) = -(4πG/3)(ρ+3P) In order for the universe to expand at an accelerated rate, the right side must be positive, and therefore (ρ+3P)must be negative. In other words, a negative mass density is needed for the universe to expand at an accelerated rate. They had negative thoughts about negative mass (negative energy). So, they discarded the negative mass (density). They corrected the equation and argued that the accelerated expansion of the universe was evidence of the existence of a cosmological constant. However, the vacuum energy model has not succeeded in explaining the value of dark energy density, and the source of dark energy has not yet been determined. They introduce negative pressure, which hides the negative mass density in the negative pressure, but this does not mean that the negative mass density has disappeared. ρ_Λ + 3P_Λ = ρ_Λ + 3(-ρ_Λ) = - 2ρ_Λ If we expand the dark energy term, the final result is a negative mass density of -2ρ_Λ. 2. Logical structure of the standard cosmology We need to look at the logic behind the success of standard cosmology. Let's look at the equation expressing (ρ+3P) as the critical density of the universe. In the second Friedmann equation (c=1), (1/R)(d^2R/dt^2) = -(4πG/3)(ρ+3P) Matter + Dark Matter (approximately 31.7%) = ρ_m ~ (1/3)ρ_c Dark energy density (approximately 68.3%) = ρ_Λ ~ (2/3)ρ_c (Matter + Dark Matter)'s pressure = 3P_m ~ 0 Dark energy’s pressure = 3P_Λ = 3(-(2/3)ρ_c ) = -2ρ_c ρ+3P≃ ρ_m +ρ_Λ +3(P_m +P_Λ)= (1/3)ρ_c +(2/3)ρ_c +3(−2/3)ρ_c= (+1)ρ_c + (-2)ρ_c = (−1)ρ_c ρ+3P ≃ (+1)ρ_c + (-2)ρ_c = (−1)ρ_c The logic behind the success of the ΛCDM model is a universe with a positive mass density of (+1)ρ_c and a negative mass density of (-2)ρ_c. So, finally, the universe has a negative mass density of “(-1)ρ_c”, so accelerated expansion is taking place. The current universe is similar to a state where the negative mass (energy) density is twice the positive mass(energy) density. And the total mass of the observable universe is the negative mass state. 3. So, what can correspond to this negative mass density? When mass or energy is present, the negative gravitational potential energy(gravitational self-energy or gravitational binding energy) produced by that mass or energy distribution can play a role. The gravitational potential energy model is a model in which +ρ(Positive energy density) and -ρ_gp(Gravitational potential energy density) exist, and shows that |-ρ_gp| can be larger than +ρ. [Result summary] Use a critical density ρ_c=8.50x10^-27[kgm^-3] At R=16.7Gly, (-M_gp)c^2 = (-0.39)Mc^2 |(-M_gp)c^2| < (Mc^2) : Decelerating expansion period At R=26.2Gly, (-M_gp)c^2 = (-1.00)Mc^2 |(-M_gp)c^2| = (Mc^2) : Inflection point (About 5-7 billion years ago, consistent with standard cosmology.) At R=46.5Gly, (-M_gp)c^2 = (-3.04)Mc^2 |(-M_gp)c^2| > (Mc^2) : Accelerating expansion period Even in the universe, gravitational potential energy (or gravitational action of the gravitational field) must be considered. And, in fact, if we calculate the value, since gravitational potential energy is larger than mass energy, so the universe has accelerated expansion. The gravitational potential energy model explains decelerating expansion, inflection points, and accelerating expansion. As the universe ages, the range of gravitational interactions increases, and thus accelerated expansion appears to have occurred because the negative gravitational potential energy increased faster than the positive mass energy. As the universe grows older, the range R of gravitational interaction increases. As a result, mass energy increases in proportion to M, but gravitational potential energy increases in proportion to -M^2/R. Therefore, gravitational potential energy increases faster. Therefore, as the universe ages and the range of gravitational interaction expands, the phenomenon of changing from decelerated expansion to accelerated expansion occurs. https://www.researchgate.net/publication/360096238_Dark_Energy_is_Gravitational_Potential_Energy_or_Energy_of_the_Gravitational_Field ----------- The accelerating expansion mechanism or inflation mechanism 1. Let’s assume that individual quantum fluctuations are born from zero energy. In this figure, the total energy of the individual quantum fluctuations that are born is 0. In figure (b), you can think of each point as an individual quantum fluctuation. For the first Δt time, it only interacts with itself gravitationally. However, as time passes, the radius of the gravitational interaction will grow to R1, R2, and R3. That is, more quantum fluctuations will enter the range of gravitational interaction, and accordingly, the total energy will change. If the mass-energy within the radius R_1 interacted gravitationally at t_1 (an arbitrary early time), the mass-energy within the radius R_2 will interact gravitationally at a later time t_2. As the universe ages, the mass-energy involved in gravitational interactions changes, resulting in changes in the energy composition of the universe. The total energy E_T of the system is In the case of a uniform distribution, comparing the magnitudes of mass energy and gravitational potential energy, it is in the form of -kR^2. That is, as the gravitational interaction radius increases, the negative gravitational potential energy value (Absolute value) becomes larger than the positive mass energy. Thus, the universe enters a period of accelerating expansion and inflation. 2.Even for a single quantum fluctuation, accelerating expansion can occur immediately, depending on the size of ΔE that changes during Δt
-
1. If the quantum fluctuations that occur do not ultimately return to nothing but continue to exist, a situation will arise where some particles are born in the vacuum and continue to exist, which will break the law of conservation of energy. If this phenomenon has already been discovered in many laboratories, it would be an important issue and would have been reported. Also, isn't Δt generally treated as the lifetime of quantum fluctuations? 2. R=ct/2 This model uses the uncertainty principle and the concept of gravitational potential energy (or gravitational self-energy). From the uncertainty principle, the physical quantity that can be treated as the range of mass distribution seems to be Δx = 2R. Since the transmission speed of gravity is known to be the speed of light, it is thought that the model can be established as 2R = cΔt or R = cΔt from gravity. However, in the case of R = cΔt, -cΔt, 0, and +cΔt exist based on the center, but it seems difficult to see that -cΔt on the left enters into a gravitational interaction with +cΔt on the right. For this reason, I thought 2R=cΔt was a better rough approximation. However, it doesn't have to be completely accurate. It's the same reason why we don't use exactly ΔxΔP≥hbar/2 in problems where we apply the uncertainty principle, but rather use an estimate like ΔxΔP ~ hbar. In this problem, I think we can set up the following three models in relation to the distribution range of mass or energy. R=cΔt/2 : transmission range of gravity, R=Δx/2 : the uncertainty principle, R=λ/2=h/2p=h/2Δp : Interaction range from matter wave concept + uncertainty principle 1)R=cΔt/2 2)R=Δx/2 3)R=λ/2=h/2p=h/2Δp In all three cases, when Δt is near t_P, the total energy of quantum fluctuations can approach 0, and thus Δt can become very large (as large as the age of the universe). On the other hand, when Δt>>t_P, the total energy ΔE_T of quantum fluctuations cannot approach 0, and therefore has a relatively short finite time Δt. Since R is included in the denominator of the gravitational potential energy, when R increases while M is constant, the absolute value of the negative gravitational potential energy term decreases. It becomes difficult to achieve zero energy, and it also becomes difficult for the accelerated expansion of the mass distribution to occur.
-
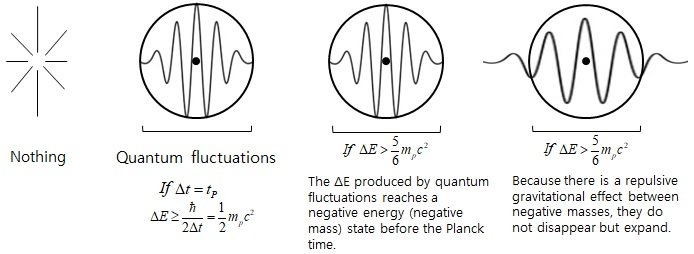
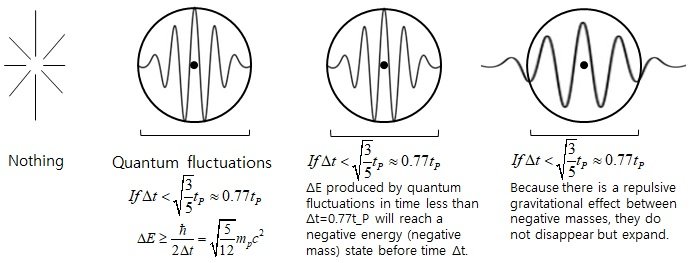
*I think there was a calculation error, so I just corrected the calculation. The core argument is the same. 3.2.3.1. Why quantum fluctuations do not return to "nothing" and form the universe The existing model of the birth of the universe from nothing claims that the universe can be born from quantum fluctuations. However, the quantum fluctuations we know should return to "nothing" after a time of Δt. The existing model of the birth of the universe from nothing do not provide a reason or mechanism for the universe to be formed without quantum fluctuations returning to "nothing". Therefore, in the case where the universe is born from quantum fluctuations, a mechanism is needed that allows the quantum fluctuations to exist and not return to "nothing". Mechanism-1. If the total energy of the system, including the gravitational potential energy, is 0 or very close to 0. If ΔE_T --> 0, Δt --> ∞ Δt where quantum fluctuations exist can be very large. In other words, Δt can be larger than the current age of the universe, and these quantum fluctuations can exist longer than the age of the universe. Since the second mechanism changes the state of quantum fluctuations, it is thought that Δt does not necessarily have to be greater than the age of the universe. If we express the gravitational potential energy in the form including ΔE, If R = cΔt/2 Therefore, in this case, we must consider gravitational potential energy or gravitational self-energy. Therefore, If ΔE_T --> 0, Δt --> ∞ . Now, let's look at the approximate Δt that can be measured with current technology in the laboratory. We can see that gravitational potential energy term is very small compared to ΔE and can be ignored. In the case of a spherical uniform distribution, the total energy of the system, including the gravitational potential energy, is Therefore, we can see that the negative gravitational potential energy is very small in the Δt (much longer than the Planck time) that we observe in the laboratory, so the total energy of the system is sufficient only by ΔE excluding the gravitational potential energy, and the lifetime of the virtual particle is only a short time given by the uncertainty principle. If Δt>>t_P, Δt≥hbar/2ΔE_T ~ hbar/2ΔE Since E_T has some finite value other than 0, Δt cannot be an infinite value, but a finite value limited by ΔE_T. However, in the early universe, a relatively large Δt is possible because ΔE_T goes to zero, and as time passes and the range of gravitational interaction expands, if the surrounding quantum fluctuations participate in the gravitational interaction, an accelerated expansion occurs. Mechanism-2. Accelerated expansion due to negative energy or negative mass state In short, According to the uncertainty principle, it is possible to change (or create) more than (1/2)m_pc^2 energy during the Planck time, If an energy change above (5/6)m_pc^2 that is slightly larger than the minimum value occurs, the total energy of the mass-energy distribution reaches negative energy, i.e., the negative mass state, within the time Δt where quantum fluctuations can exist. However, since there is a repulsive gravitational effect between negative masses, the corresponding mass distribution expands instead of contracting. Thus, the quantum fluctuations generated by the uncertainty principle cannot return to nothing, but can expand and create the present universe. * Motion of positive mass due to negative gravitational potential energy, The force exerted by a negative (equivalent) mass on a positive mass is a repulsive (anti-gravity) force, so the positive mass accelerates and expands. The gravitational force acting between negative masses is attractive(m>0, F= - G(-m)(-m)/r^2 = - Gmm)/r^2), but since the inertial mass is negative in the case of negative mass, the gravitational effect is repulsive(m>0, F= (-m)a, a = - F/m ). So the distribution of negative energy or the distribution of negative equivalent mass is inflated. In a state of uniform energy distribution, when time passes, the radius of gravitational interaction increases. In this case, the mass energy increases in proportion to M, but the size of the gravitational potential energy increases in proportion to M^2/R. Therefore, since the negative gravitational potential energy increases faster than the positive mass energy, the phenomenon of accelerated expansion can occur. By combining mechanisms 1 and 2, we can simultaneously explain the existence of a universe born from quantum fluctuations without returning to "nothing", and the problem of inflation in the early universe. =============== I will write the answer to this question after I do what I have to do first. Within 1 day~
-
3.2.3.1. Why quantum fluctuations do not return to "nothing" and form the universe The existing model of the birth of the universe from nothing claims that the universe can be born from quantum fluctuations. However, the quantum fluctuations we know should return to "nothing" after a time of Δt. The existing model of the birth of the universe from nothing do not provide a reason or mechanism for the universe to be formed without quantum fluctuations returning to "nothing". Therefore, in the case where the universe is born from quantum fluctuations, a mechanism is needed that allows the quantum fluctuations to exist and not return to "nothing". Mechanism-1. If the total energy of the system, including the gravitational potential energy, is 0 or very close to 0. If ΔE_T --> 0, Δt --> ∞ Δt where quantum fluctuations exist can be very large. In other words, Δt can be larger than the current age of the universe, and these quantum fluctuations can exist longer than the age of the universe. Since the second mechanism changes the state of quantum fluctuations, it is thought that Δt does not necessarily have to be greater than the age of the universe. If we express the gravitational potential energy in the form including ΔE, If R = cΔt/2 ΔE_min means the minimum energy fluctuation that satisfies the equation ΔE≥hbar/2Δt. If Δt=t_P, U_gp ≥ -(3/5)ΔE_min Therefore, in this case, we must consider gravitational potential energy or gravitational self-energy. Therefore, If ΔE_T --> 0, Δt --> ∞ . Now, let's look at the approximate Δt that can be measured with current technology in the laboratory. We can see that gravitational potential energy term is very small compared to ΔE and can be ignored. In the case of a spherical uniform distribution, the total energy of the system, including the gravitational potential energy, is Therefore, we can see that the negative gravitational potential energy is very small in the Δt (much longer than the Planck time) that we observe in the laboratory, so the total energy of the system is sufficient only by ΔE excluding the gravitational potential energy, and the lifetime of the virtual particle is only a short time given by the uncertainty principle. If Δt>>t_P, Δt≥hbar/2ΔE_T ~ hbar/2ΔE Since E_T has some finite value other than 0, Δt cannot be an infinite value, but a finite value limited by ΔE_T. However, in the early universe, a relatively large Δt is possible because ΔE_T goes to zero, and as time passes and the range of gravitational interaction expands, if the surrounding quantum fluctuations participate in the gravitational interaction, an accelerated expansion occurs. Mechanism-2. Accelerated expansion due to negative energy or negative mass state In short, According to the uncertainty principle, it is possible to change (or create) more than (1/2)m_pc^2 energy during the Planck time, If an energy change above (5/6)m_pc^2 that is slightly larger than the minimum value occurs, the total energy of the mass-energy distribution reaches negative energy, i.e., the negative mass state, within the time Δt where quantum fluctuations can exist. However, since there is a repulsive gravitational effect between negative masses, the corresponding mass distribution expands instead of contracting. Thus, the quantum fluctuations generated by the uncertainty principle cannot return to nothing, but can expand and create the present universe. * Motion of positive mass due to negative gravitational potential energy, The force exerted by a negative (equivalent) mass on a positive mass is a repulsive (anti-gravity) force, so the positive mass accelerates and expands. The gravitational force acting between negative masses is attractive(m>0, F= - G(-m)(-m)/r^2 = - Gmm)/r^2), but since the inertial mass is negative in the case of negative mass, the gravitational effect is repulsive(m>0, F= (-m)a, a = - F/m ). So the distribution of negative energy or the distribution of negative equivalent mass is inflated. In a state of uniform energy distribution, when time passes, the radius of gravitational interaction increases. In this case, the mass energy increases in proportion to M, but the size of the gravitational potential energy increases in proportion to M^2/R. Therefore, since the negative gravitational potential energy increases faster than the positive mass energy, the phenomenon of accelerated expansion can occur. By combining mechanisms 1 and 2, we can simultaneously explain the existence of a universe born from quantum fluctuations without returning to "nothing", and the problem of inflation in the early universe.
-
If the universe was nothing at the beginning, how did this state of nothing then create what is the universe? We don't yet know what the answer is. However, because it is an important issue, I am writing my personal opinion. Let's start with the following equation: A = A Before the universe was birthed, the concept of A did not even exist. This A is an concept created by intellectual creature called humanity, 13.8 billion years after the creation of the universe. Also, mathematical terms, including =, are concepts created by humans born after the birth of the universe. If we move "A" from the left side to the right side, 0 = A - A = 0 To make the idea clearer, let's express this a little differently. 0 = (+A) + (-A) = 0 This equation can be conceptually decomposed as "0", "0=(+A)+(-A)", "(+A)+(-A)=0", "0=0". 1)"0" : Something did not exist. Nothing state. 2)"0 = (+A) + (-A)" : (+A) and (-A) were born from "nothing". Or "nothing" has changed to +A and -A. Something state. 3)"(+A) + (-A) = 0" : The sum of (+A) and (-A) is still zero. From one perspective it's "something state", from another perspective it's still “nothing state”. 4)"0 = 0" At the beginning and end of the process, the state of “nothing” is maintained. 5) "B = 0 = (+A) + (-A) = 0" : The intelligent life form called humanity defines the "first nothing" as B. B may be total A, which is the sum of all A, or it may be a new notion. In other words, “nothing” can create something +A and something -A and still remain “nothing” state. And, the newly created +A and -A create new physical quantities and new changes. For example, in order for the newly created +A and -A to be preserved in space, a new relational equation such as a continuity equation must be created. ∂ρ/∂t + ∇·j=0 Let's look at how pair production occurs from photon (light). B = 0 = (+Q) + (-Q) = 0 The charge of a photon is zero. When photon do pair production, photon do not conserve charge by creating beings with zero charge, but by creating +Q and -Q to preserve zero. That is, in all cases, in all circumstances, in order to satisfy or maintain “nothing”, this equation of the form (+Q) + (-Q) = 0 must hold. This may be because "0" is not representative of all situations and is only a subset of (+Q) + (-Q) = 0. At the beginning and end of the process, the total charge is conserved, but in the middle process +Q and -Q are created. Due to the electric charge generated at this time, new concepts including electromagnetic fields and electromagnetic forces are needed. According to Emmy Noether's theorem, if a system has a certain symmetry, there is a corresponding conserved physical quantity. Therefore, symmetry and conservation laws are closely related. Conservation of spin, conservation of particle number, conservation of energy, conservation of momentum, conservation of angular momentum, conservation of flux... etc.. New concepts may be born from conservation laws like these. Let’s look at the birth process of energy. https://icarus2.quora.com/The-Birth-Mechanism-of-the-Universe-from-Nothing-and-New-Inflation-Mechanism E_T = 0 = (+E) + (-E) = Σmc^2 + Σ(-Gmm/r) = 0 “E_T = 0” represents “Nothing” state. Mass appears in “Σ(+mc^2)” stage, which suggests the state of “Something”. In other words, “Nothing” produces a negative energy of the same size as that of a positive mass energy and can produce “Something” while keeping the state of “Nothing” in the entire process (“E_T = 0” is kept both in the beginning of and in the end of the process). Another example is the case of gauge transformation for scalar potential Φ and vector potential A in electromagnetic fields. Φ --> Φ - ∂Λ/∂t A --> A + ∇Λ Maxwell equations of electromagnetism hold them in the same form for gauge transformation. After all, the existence of some symmetry or the invariance that the shape of a certain physical law must not change requires a gauge transformation, and this leads to the existence of new physical quantities (Λ, ∂Λ/∂t, ∇Λ) that did not exist in the beginning (Φ, A). This can be interpreted as requiring the birth of a new thing in order for the conserved physical quantity to be conserved and not change. The condition or state that should not change is what makes change. Why was the universe born? Why is there something rather than nothing? Why did the change happen? B = 0 = (+Q) + (-Q) = 0 E_T = 0 =(+E) + (-E) = Σmc^2 + Σ-Gmm/r = 0 ∂ρ/∂t + ∇·j=0 Φ --> Φ - ∂Λ/∂t A --> A + ∇Λ It changes, but does not change! It changes in order not to change! What does not change (B = 0) also creates changes in order not to change in various situations (Local, Global, phase transformation, translation, time translation, rotation transformation ...). This is because only the self (B) that does not want to change needs to be preserved. The change of the universe seems to have created a change by the nature of not changing. The universe created Something (space-time, quantum fluctuation, energy, mass, charge, spin, force, field, potential, conservation laws, continuity equation...) to preserve Nothing. By the way, as this something was born, another something was born, and the birth of something chained like this may still preserve the first "nothing", and in some cases, the first "nothing" itself may also have changed.
-
Mathematics began as human intellectual activity to describe phenomena that exist in nature and the universe. Therefore, mathematics and the universe have a very deep connection, and events that occur in the universe can generally be described through mathematics. However, in mathematics, if a proposition is true within a defined axiomatic system, then this proposition is true and has value. In other words, because mathematics reflects human intellectual activity, even things that are imaginary can become true. On the other hand, the universe is true to exist and has value. Therefore, mathematics and the universe are not completely the same thing.
-
Pressure, energy, and mass are all sources of gravity. Therefore, these terms enter the Friedmann equation and play the role of -(4πG/3)p, which is the gravitational effect. According to Birkhoff’s theorem, The first Friedmann equation without a cosmological constant is derived from general relativity, but there is also a form derived from the conservation of mechanical energy of Newtonian mechanics (dust model), and this is taught in major books. At this time, the terms entered are kinetic energy and gravitational potential energy. [math]\frac{1}{2}m{v^2}(t) - G\frac{{{M_r}m}}{{r(t)}} = E[/math] Therefore, the right-hand side term (8πG/3)ρ comes from the total mass M_r inside the shell. Friedmann's second equation without a cosmological constant is also derived from general relativity, but can also be derived from F=ma=-GMm/R^2. This also uses gravitational force. Because this is intuitive, if we look at this derivation process [math]ma = - \frac{{GMm}}{{{R^2}}}[/math] [math]m\frac{{{d^2}R(t)}}{{d{t^2}}} = - \frac{{GM(t)m}}{{R{{(t)}^2}}}[/math] [math]M(t) = \frac{{4\pi {R^3}(t)}}{3}\rho (t) = \frac{{4\pi {a^3}(t){R^3}}}{3}\rho (t)[/math] [math]m\frac{{{d^2}a(t)R}}{{d{t^2}}} = - Gm\frac{{\frac{{4\pi }}{3}{a^3}(t){R^3}\rho (t)}}{{{a^2}(t){R^2}}} = - Gm\frac{{4\pi }}{3}a(t)R\rho (t)[/math] [math]\frac{{\ddot a(t)}}{{a(t)}} = - \frac{{4\pi G}}{3}\rho (t)[/math] Adding pressure, we can create an acceleration equation. [math]\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}(\rho + \frac{{3P}}{{{c^2}}})[/math] In other words, we can see that ρ(t) is the mass density inside the expanding shell, and the -(4πG/3)ρ term describes gravity or gravitational effects. It can be seen that the total mass M inside the shell is included in both Friedmann equations 1 and 2. This means that the equivalent mass of total energy is included. If matter and radiation have the same energy density ρ0, it is thought that they should be the same when entering the acceleration equation. In my opinion, We can put in the equivalent mass of the energy density of the radiation divided by c^2, and let the pressure of the radiation be 0, or since the rest mass of the radiation is 0, let the mass density be 0, and in the pressure term (1/3)ρ must be inserted. Photons are also included as relativistic particles. However, in this explanation, I tried to distinguish between relativistic particles that have rest mass and photons that do not have rest mass. For photons, which do you think is correct: 1ρ0 or 2ρ0 ?
-
Consider a situation where matter and radiation have the same energy density ρ_0. If we set c=1, mass density = energy density For matter, [math]{\rho _m} + 3P{}_m = {\rho _m} + 3(0) = {\rho _m} = {\rho _0}[/math] For radiation (photon), [math]{\rho _r} + 3P{}_r = {\rho _r} + 3(\frac{1}{3}{\rho _r}) = 2{\rho _r} = 2{\rho _0}[/math] Now if we think about the physical meaning of the two cases, This means that if matter and radiation have the same energy density ρ_0, the gravitational effect of the radiation is twice that of the matter. If photon and matter have the same energy density, does the photon exert twice the gravitational force (or effect) than the material exerts? Is this true? In my opinion, In the case of photon, it seems wrong to include both density in the (mass) density term and pressure term.
-
I think I didn't phrase the question appropriately. [math]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}({\rho _m} + {\rho _r} + {\rho _\Lambda } + \frac{{3({P_m} + {P_r} + {P_\Lambda })}}{{{c^2}}})[/math] [math]\rho + \frac{{3P}}{{{c^2}}} = ({\rho _m} + \frac{{3P{}_m}}{{{c^2}}}) + ({\rho _r} + \frac{{3P{}_r}}{{{c^2}}}) + ({\rho _\Lambda } + \frac{{3P{}_\Lambda }}{{{c^2}}})[/math] In this question the first and third terms are not of interest. What happens if you summarize(Energy density of photon ρ) the second term? When the energy density of a photon is ρ, I am curious as to whether its gravitational effect in the acceleration equation is 1ρ or 2ρ. *When considering the dimension, it must be divided by c^2, but this is not an important issue. [math]{\rho _r} + \frac{{3P{}_r}}{{{c^2}}} = [/math]
-
Gravitational effect and pressure of photons in Friedmann equation? [math] \frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}({\rho _m} + {\rho _r} + {\rho _\Lambda } + \frac{{3({P_m} + {P_r} + {P_\Lambda })}}{{{c^2}}}) [/math] ρ is the unit of mass density. Pressure of matter : P=0 Pressure of radiation : P=(1/3)ρc^2 Regarding the source of pressure, there are the following expressions in major books: In special relativity, [math]{E^2} = {({m_0}{c^2})^2} + {(pc)^2}[/math] For matter, [math]{E^2} = {({m_0}{c^2})^2}[/math] For, relativistic particle, [math]{E^2} = {({m_0}{c^2})^2} + {(pc)^2}[/math] For, radiation or photon, [math]{E^2} = {(pc)^2}[/math] So, here's the question. For a relativistic particle with rest mass it would be: [math]{E^2} = {({m_0}{c^2})^2} + {(pc)^2}[/math] In the case of relativistic particles, there is a pressure component due to kinetic energy or momentum, and this value cannot be ignored compared to mass energy. [math]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}({\rho _{{\rm{relativistic particle}}}} + \frac{{3{P_{{\rm{relativistic particle}}}}}}{{{c^2}}}) = - \frac{{4\pi G}}{3}({\rho _{{\rm{rel - par}}}} + \frac{{3(\frac{1}{3}{\rho _{{\rm{rel - par}}}}{c^2})}}{{{c^2}}}) = - \frac{{4\pi G}}{3}(2{\rho _{{\rm{rel - par}}}})[/math] [math]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}(2{\rho _{{\rm{rel - par}}}}) = - \frac{{4\pi G}}{3}(\frac{{2{\rho _{{\rm{rel - par}}}}{c^2}}}{{{c^2}}})[/math] When the energy density of matter is ρ, in the Friedmann equation, matter generates the gravitational effect of ρ. When the energy density of a relativistic particle is ρ, in the Friedmann equation, the relativistic particle generates a gravitational effect of 2ρ. But what about photons, which are not relativistic particles? Which expression is correct for photons that have no rest mass? 1) [math]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}({\rho _{rad}} + \frac{{3(\frac{1}{3}{\rho _{rad}}{c^2})}}{{{c^2}}}) = - \frac{{4\pi G}}{3}(2{\rho _{{\rm{rad}}}}) = - \frac{{4\pi G}}{3}(\frac{{2{\rho _{{\rm{rad}}}}{c^2}}}{{{c^2}}})[/math] Considering radiation(When limited to photons) with energy density ρ, it generates a gravitational effect equal to twice the energy density : 2ρ ? 2) [math]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - \frac{{4\pi G}}{3}({\rho _{{\rm{radiation}}}} + \frac{{3{P_{{\rm{radition}}}}}}{{{c^2}}}) = - \frac{{4\pi G}}{3}(0 + \frac{{3(\frac{1}{3}{\rho _{rad}}{c^2})}}{{{c^2}}}) = - \frac{{4\pi G}}{3}({\rho _{{\rm{rad}}}}) = - \frac{{4\pi G}}{3}(\frac{{{\rho _{{\rm{rad}}}}{c^2}}}{{{c^2}}})[/math] Considering radiation(When limited to photons) with energy density ρ, it generates a gravitational effect equal to 1 times the energy density : 1ρ ? 1) Is the expression correct? 2) Is the expression correct?
-
In the post just above, Even if there was no energy before the Big Bang, enormous amounts of energy can be created due to the uncertainty principle. In a region smaller than the size of an atomic nucleus, the total mass-energy that exists in the observable universe can be created. In the early universe, when only positive mass energy is considered, the mass energy value appears to be a very large positive energy, but when negative gravitational potential energy is also considered, the total energy can be zero and even negative energy. Considering not only mass energy but also gravitational potential energy, the total energy of the system is According to the uncertainty principle, during Planck time, energy fluctuations of more than (1/2)m_pc^2 are possible. However, let us consider that an energy of ΔE=(5/6)m_pc^2, slightly larger than the minimum value, was born. 1) If, Δt=t_p, ΔE=(5/6)m_pc^2, The total energy of the system is 0. In other words, a mechanism that generates enormous mass (or energy) while maintaining a Zero Energy State is possible. 2) If, Δt=(3/5)^(1/2)t_p, ΔE≥(5/12)^(1/2)m_pc^2, The total energy of the system is 0. In other words, a mechanism that generates enormous mass (or energy) while maintaining a Zero Energy State is possible. This is not to say that the total energy of the observable universe is zero. This suggests that enormous mass energy can be created from a zero energy state in the early stages of the universe. In this way (If we are limited to what is explained in this post~), the total energy of one quantum fluctuation is zero energy. Since individual quantum fluctuations are born in a zero energy state, and as time passes, the range of gravitational interaction expands, when surrounding quantum fluctuations come within the range of gravitational interaction, accelerated expansion occurs by this method. This method uses the minimum value of energy fluctuations. On the other hand, at energies greater than the minimum, expansion can occur even from a single quantum fluctuation. Through this model, we can simultaneously solve the problem of the origin of enormous energy and the problem of accelerated expansion in the early stages of the universe.
-
A combined model of the uncertainty principle and gravitational potential energy provides an explanation for how the universe was born and expanded in a dense state. [math] \Delta E\Delta t \ge \frac{\hbar }{2}[/math] From the energy-time uncertainty principle, If, [math]\Delta t \approx {t_P} = 5.391 \times {10^{ - 44}}s[/math] [math]\Delta E \ge \frac{\hbar }{{2\Delta t}} = \frac{\hbar }{{2{t_P}}} = \frac{1}{2}m{}_P{c^2}[/math] Δx=ct_p=2R’ : Since Δx corresponds to the diameter of the mass distribution Assuming a spherical mass distribution and calculating the average mass density (minimum value), [math]\frac{1}{2}{m_P} = \frac{{4\pi {{R'}^3}}}{3}{\rho _0} = \frac{{4\pi {{(\frac{{c{t_P}}}{2})}^3}}}{3}{\rho _0}[/math] [math]{\rho _0} = \frac{3}{\pi }\frac{{{m_P}}}{{{l_P}^3}} = \frac{3}{\pi }{\rho _P} \simeq 4.924 \times {10^{96}}kg{m^{ - 3}}[/math] It can be seen that it is extremely dense. In other words, the quantum fluctuation that occurred during the Planck time create energy with an extremely high density. The total mass of the observable universe is approximately 3.03x10^54 kg (used to ρ_c=8.5x10^-27 kg/m^3), and the size of the region in which this mass is distributed with the initial density ρ_0 is R_obs-universe (ρ=ρ_0) = 5.28x10^-15 [m] This value is approximately the size of an atomic nucleus. Not all models can account for the high dense state of the early universe. Also, not all models can provide repulsion or expansion to overcome the very strong gravity in this high-density state. So it's a decent result. [ Verifiability ] As a key logic to the argument of this paper, gravitational potential energy appears, and the point where the magnitude of the negative gravitational potential energy equals the positive mass energy becomes an inflection point, suggesting that the accelerated expansion period is entered. [math]{R_{gs}} = \sqrt {\frac{{5{c^2}}}{{4\pi G{\rho _0}}}} [/math] Since we can let R_gs be approximately ct(for a space with uniform energy (mass) density) or cΔt/2(with the uncertainty principle applied, if the energy (mass) distribution enters an accelerated expansion within Δt), there is a strong constraint equation between the density and the time the universe entered accelerated expansion. Therefore, it is possible to verify the model through this. It is necessary to create an early universe accelerating expansion model to which the ideas in this paper are applied. When such precise models come out, there will be more factors that can verify the model's accuracy.
-
*Revision Mass energy is of the form \(E=Mc^{2}\) and remains constant. On the other hand, the gravitational potential energy is of the form \({U_{gs}} = - \frac{3}{5}\frac{{G{M^2}}}{R}\), and the absolute value decreases as R increases. Therefore, when the mass distribution expands, only the absolute value of the negative gravitational potential energy term decreases, so the system switches to the positive mass state after \(R=R_{gs}\). The reduced gravitational potential energy will be converted into kinetic energy. For example, if the mass in the system is constant and R (R is the radius of the mass distribution) doubles from \(R_0\) to \(2R_0\), it can be seen that the absolute value of the gravitational self-energy is reduced by a factor of \(\frac{1}{2}\).
-
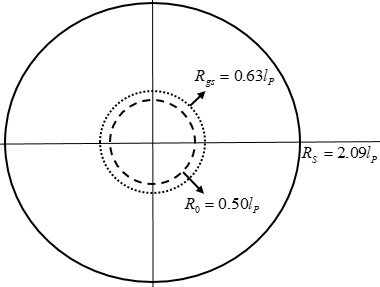
3.6. The Vacuum Catastrophe Problem or Cosmological Constant Problem The vacuum catastrophe problem or the cosmological constant problem is a problem in which there is a large difference between the theoretical prediction of vacuum energy proposed by quantum field theory and the observed value. It is known that there is a difference of about 10^120 between theoretical predictions and observed values. Strictly speaking, the vacuum energy model is only one of the dark energy models, so the observed (or estimated from observed results) dark energy density may not be the density of vacuum energy. Therefore, the actual vacuum energy density can be the dark energy density, or zero, or negative. However, if the density of vacuum energy is greater than the dark energy density, it will have a larger effect than the dark energy term, so it can be excluded by observational results. Therefore, the upper limit of the observed vacuum energy density is approximately the dark energy density, and there is still a difference of more than 10^120 times between the theoretical prediction value and the actual vacuum energy density value. First, looking at the claims of the vacuum energy model, Since there is energy ΔE or u_{vac}, which is one of the sources of gravity, and there is time Δt for gravity to propagate, the gravitational self-energy must also be considered in this problem. So, to look at the mainstream estimates in terms of my model, let's do some calculations. We have an equation for calculating the total gravitational potential energy in the case of a spherical, uniform distribution. This value is called the gravitational self-energy. In the vacuum energy model, calculations were performed as a regular hexahedron with one side L. If we consider a spherical space inside a regular hexahedron, the value of the vacuum energy density will be the same in this case. Since there is an expression for gravitational self-energy already calculated for spherical space, to utilize it, let's consider a spherical energy (mass) distribution with \(R = \frac{L}{2}\). According to the mass-energy equivalence principle, it is possible to define the equivalent mass (m = E/c^2) for all energies. Therefore, in this paper, the terms equivalent mass energy or mass energy or mass are sometimes used for objects with positive energy. 3.6.1. Vacuum energy in space R = L/2 [math]{E_{vac}} = \frac{{4\pi {R^3}}}{3}{u_{vac}} = \frac{{4\pi {{(\frac{L}{2})}^3}}}{3}(\frac{{2{c^7}}}{{\hbar {G^2}}}) = \frac{{4\pi {{(\frac{\hbar }{{2{m_P}c}})}^3}}}{3}(\frac{{2{c^7}}}{{\hbar {G^2}}}) = \frac{\pi }{3}{m_P}{c^2}[/math] [math]{E_{vac}} = \frac{\pi }{3}{m_P}{c^2} \simeq + 1.047{m_P}{c^2}[/math] 3.6.2. The gravitational potential energy of the vacuum energy of space R = L/2 [math]{U_{gs}} = - \frac{3}{5}\frac{{G{M^2}}}{R} = - \frac{3}{5}\frac{{G{{(\frac{\pi }{3}{m_P})}^2}}}{{\frac{L}{2}}} = - \frac{3}{5}\frac{{G{{(\frac{\pi }{3}{m_P})}^2}}}{{(\frac{\hbar }{{{2m_P}c}})}} = - \frac{{2{\pi ^2}}}{{15}}{m_P}{c^2}[/math] [math]{U_{gs}} = - \frac{{2{\pi ^2}}}{{15}}{m_P}{c^2} \simeq - 1.316{m_P}{c^2}[/math] 3.6.3. The event horizon created by vacuum energy \({E_{vac}} = \frac{\pi }{3}{m_P}{c^2}\) [math]{R_S} = \frac{{2GM}}{{{c^2}}} = \frac{{2G(\frac{\pi }{3}{m_P})}}{{{c^2}}} = \frac{{2\pi }}{3}{l_P} \simeq 2.094{l_P}[/math] 3.6.4. The radius R_gs at which the magnitudes of positive mass energy and negative gravitational potential energy are equal [math]|\frac{{{U_{gs}}}}{{{E_{vac}}}}| = |\frac{{ - \frac{3}{5}\frac{{G{{(\frac{\pi }{3}{m_P})}^2}}}{R}}}{{\frac{\pi }{3}{m_P}{c^2}}}| = | \frac{{\frac{\pi }{5}\frac{{G{m_P}}}{{{c^2}}}}}{R}| = 1 [/math] [math] {R_{gs}} = \frac{\pi }{5}{l_P} = 0.628{l_P} [/math] 3.6.5. Physical meaning of calculated R values [math] {E_T}(t = \Delta t) = {E_{vac}} + {U_{gs}} = \frac{\pi }{3}{m_P}{c^2} - \frac{{2{\pi ^2}}}{{15}}{m_P}{c^2} \simeq - 0.269{m_P}{c^2} < 0 [/math] Initially, since the negative gravitational potential energy is greater than the positive mass energy, the mass distribution at \({R_0} = \frac{L}{2}\) will expand. If there is no additional mass influx (or if mass is held constant), when the expanding mass distribution passes \(R_{gs}\), the negative gravitational potential energy equals the positive mass energy. When the mass distribution becomes larger than R_gs, since the positive mass energy is greater than the negative gravitational potential energy, the system switches to the positive mass state, and thus the situation in which the attractive force acts. Thus, the mass distribution will contract back to R_gs. Mass energy is of the form E=Mc^2 and remains constant. On the other hand, the gravitational potential energy is of the form \({U_{gs}} = - \frac{3}{5}\frac{{G{M^2}}}{R}\), which decreases as R increases. Therefore, when the mass distribution expands, only the negative gravitational potential energy term decreases, so the system switches to the positive mass state after R=R_gs. The reduced gravitational potential energy will be converted into kinetic energy. For example, if the mass in the system is constant and R (R is the radius of the mass distribution) doubles from R_0 to 2R_0, it can be seen that the gravitational self-energy is reduced by a factor of 1/2. [math] {U_{gs}}(R = {R_0}) = - \frac{3}{5}\frac{{G{M^2}}}{{{R_0}}} [/math] [math] {U_{gs}}(R = 2{R_0}) = - \frac{3}{5}\frac{{G{M^2}}}{{2{R_0}}} = \frac{1}{2}{U_{gs}}(R = {R_0}) [/math] R < R_gs : system is in negative energy (mass) state. Since the repulsive force component is greater than the attractive force component, the mass distribution expands. R > R_gs : The system is in a positive energy (mass) state. Since the attractive force component is greater than the repulsive force component, the mass distribution undergoes deceleration expansion and contraction. Therefore, the mass distribution becomes stable at R=R_gs while oscillating around R=R_gs. The point where R=R_gs is the point where the total energy of the system is zero. One of the important characteristics is that it vibrates (repeating acceleration and deceleration expansion) based on R=R_gs, and finally stabilizes at R=R_gs. This is because the R=R_gs point is the point where the positive and negative energy components are equal, and the total energy of the system is zero. Although we are analyzing the process in detail, the time interval between these events is approximately t_P ~ 10^{-44}s. As a rough estimate, if there is no additional mass density generation within the 1l_P(Planck length, approximately 2(0.50(l_P))) range, the mass distribution will converge to R_gs where the positive mass energy equals the negative gravitational potential energy. As a result, the mass distribution returns to the zero-energy state because the magnitudes of the positive mass energy and the negative gravitational self-energy in R_gs are equal. Also, since the event horizon R_S=2.09(l_P) formed by the mass distribution of R_0 is greater than R_gs=0.63(l_P), the mass distribution exists inside the event horizon. Therefore, the mass distribution does not escape the event horizon, converges to R_gs, and finally returns to nothing. And, as a problem of consideration, when a stellar black hole forms, the space-time outside the black hole is affected and curved during the process of forming the black hole. By the way, after forming the black hole, if the location of the mass distribution changes inside the black hole, does this also affect the space-time outside the black hole? It is estimated that gravity due to changes in the distribution of mass inside the black hole will not be able to escape the black hole. Even when gravity due to changes in the mass distribution inside the black hole affects the geometry of space-time outside the black hole, the effect is zero or very close to zero because of the gravitational properties of negative gravitational potential energy and positive mass energy described above. As in previous theoretical calculations, if the vacuum had an enormous energy of \({u_{vac}} \approx {10^{111}} \sim {10^{114}}J{m^{ - 3}}\), it should be observable around us. However, we are not detecting the presence of these enormous energies from the vacuum. Even if quantum fluctuations occur in vacuum according to existing theoretical assumptions, since ΔE and Δt exist, their own gravitational interactions must also be taken into account. Therefore, considering the gravitational self-energy, the vacuum energy density is likely to be zero, unless the frequency of quantum fluctuations in the vacuum is extremely high. If the frequency of occurrence of quantum fluctuations is less than approximately 1 within the range of radius l_P during the 5t_P(rough estimate), it can be estimated that the total energy of the quantum fluctuations produced will be in the zero energy. For example, as a rough estimate, let's assume that 1 quantum fluctuation occurs within a radius of 1(l_P, Planck length ) in 100(t_P) time. Even in this case, it suggests a return to the zero energy state by the above mechanism.This is the case assuming an enormous number of quantum fluctuations. This situation corresponds to the assumption of approximately 10^147 ( 100{t_P} ~10^{-42}s, 2(1{l_P}) ~ 10^{-35}m, Volume ~ 10^{-105}m^3) quantum fluctuations per second, in a space of 1m^3. Thus, vacuum energy is not a source of dark energy. If the problem is a simple situation that cannot explain the difference in density of 10^120, the possibility remains that the difference in density can be explained by some mechanism at some point in the future. The real problem with vacuum energy model is, First, that positive energy density (positive inertial mass density) and negative pressure are logically contradictory because the source of pressure is momentum or kinetic energy. Second, even in the case of light with the greatest momentum or kinetic energy component relative to the total energy, the pressure is \(P = \frac{1}{3}\rho \). The claims of the vacuum energy model require a being with a momentum or kinetic energy three times (\({P_\Lambda } = - {\rho _\Lambda } = - 3(\frac{1}{3}{\rho _\Lambda })\)) greater than that of light. Third, it is a problem related to the logic of \({\rho _\Lambda } + 3{P_\Lambda } = {\rho _\Lambda } + 3( - {\rho _\Lambda }) = - 2{\rho _\Lambda }\). Mass density ρ and pressure P are properties that an object has. Also, mass density ρ and pressure P are the sources of gravity. However, even if the volume does not expand or contract and maintains a constant size, it means that the gravitational force of \({\rho _\Lambda } + 3{P_\Lambda } = - 2{\rho _\Lambda }\) is applied. That is, it suggests that the object (or energy density) has a gravitational force with a negative mass density of -2ρ_Λ. This is different from a vacuum, which we think has a positive energy density +ρ_Λ. Fourth, it also seems that there is a problem in applying dU = - PdV to vacuum energy. And, there are models that are 10^120 more accurate than the vacuum energy model. The Birth Mechanism of the Universe from Nothing and New Inflation Mechanism https://www.researchgate.net/publication/371951438
-
Inline math is displayed in the flow of a sentence \(m{c^2}\). hm [math] y = \int f(x) dx [/math] Inline brackets: \( y = x^2 \) Inline brackets: \[ y = x^2 \]
-
First of all, thank you for your sincere advice. Actually I lack knowledge and skills. My research is a personal hobby. It is true that I need to study more to make my hobby more meaningful. However, on the other hand, should I have to study hard to enjoy my hobby? Even if I study, there is still a high entry barrier, and I am not sure if I will overcome the entry barrier. As for my current interests, I have some interest in publishing my research on arXiv or mainstream journals. arXiv requires endorsements from other scientists. Even with the endorsement of another scientist, the administrator will delete it arbitrarily. I've had that process a few times, so, now I don't even try. I think this paper contains very cool ideas and is worthwhile. By any chance, do you have any intention of summarizing the content of my thesis in half and submitting it to a journal as a corresponding author? I can also solve the vacuum catastrophe problem! However, the result may not be what you expect. However, it is a solution that did not exist before, and it will be a pioneer of a new path. Vacuum catastrophe problem has not yet been added to this thesis. I will update this post with that in a week or less. Once again, thank you for your goodwill.
-
That part introduces beings with energy just to explain the characteristics of gravitational potential energy. The situation in which universe exists after birth from zero energy is the content of chapter 4.1 ~ 4.2. Of course, it is not completely nothing because it assumes the existence of principles of physics such as the uncertainty principle, but the term "nothing" is sometimes used in that it starts from zero energy.
-
The phrase I wrote is this. In Figure 1, if the mass-energy within the radius R_1 interacted gravitationally at t_1 (an arbitrary early time), the mass-energy within the radius R_2 will interact gravitationally at a later time t_2. As the universe ages, the mass-energy involved in gravitational interactions changes, resulting in changes in the energy composition of the universe. The total energy $E_{T}$ of the system is [math]{E_T} = \sum\limits_i {{m_i}{c^2}} + \sum\limits_{i < j} { - \frac{{G{m_i}{m_j}}}{{{r_{ij}}}}} = M{c^2} - \frac{3}{5}\frac{{G{M^2}}}{R}[/math] And, it is a matter of interpreting mass-energy as a being with mass or energy. It's just a summary of a 24-pages thesis. And, in the introduction of the thesis, there are the following passages: In addition, although there are electric charges, spins, and various physical quantities, it is necessary to analyze the problem of expanding the universe due to gravitational interactions because the object will be a being with at least energy (mass) even in various situations. I'm sorry for you too. I didn't understand what you meant. I misunderstood this sentence(As mentioned energy is the property describing the ability to perform work. It isn't something that exists on its own.) you wrote. I am so sorry. The total energy E_{T} of the system And, mass-energy means a being with mass or energy.
-
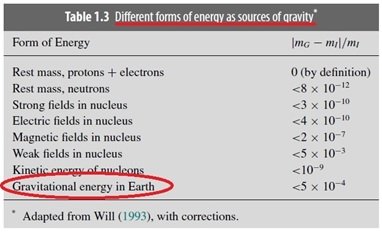
I think this claim( It isn't something that exists on its own.) about potential energy is false. Potential energy should be treated as real energy, not virtual energy. Potential energy must have a specific value under specific circumstances. 1. In the calculation of potential energy, not only the calculation through the amount of change is successful. Calculations with own values(I don't know what to choose as the right word. own value?) also succeed. In other words, even if the calculation through the change is successful, it does not guarantee that it is correct. U=mgh or U=-GMm/r 2. Looking at the electromagnetic potential energy similar to the gravitational potential energy, + + or - - : When the same kind of charge exists, [math]{U_{ + + }} = + \frac{{k{q_1}{q_2}}}{r} + {c_1}[/math] + - : When charges of different species exist, [math]{U_{ + - }} = - \frac{{k{q_1}{q_2}}}{r} + {c_2}[/math] 1)The situation where +Q+Q and +Q-Q exist seems to be a symmetrical situation, should c1, c2 exist? 2)Let's assume that the constants are the same as c1=c2, + + : When same kind charges exist, U=+kq1q2/r +c1 + - : When charges of different kinds exist, U=-kq1q2/r + c1 Does this asymmetry look right? 3. In elementary particle physics, invariant mass includes either binding energy or potential energy, depending on how the system is defined. It is well known that when proton-neutrons make up a nucleus, they have less mass than they do in their free state. Since these protons and neutrons do not change their mass in the coordinate system of their center of mass, they are rest mass and invariant mass in this situation. However, when they form one nucleon, the mass decreases by the difference in binding energy. In other words, the constant mass of one nucleon has a negative binding energy. Now there's the matter of combining nucleons with other nucleons, then the individual nucleons have an invariant mass. This is because, in the coupling problem of two nucleons, individual nucleons are assumed to be invariant in the coordinate system of the center of mass of the individual nucleons. I think we need to think about the meaning of the fact that the binding energy is included in the rest mass of the composite particle. In composite particles, binding energy is also a component of invariant mass. Should we treat these objects as objects that do not have any own value (fixed value), as objects that have values only when changes occur without substance? Since almost all problems related to potential energy are problems of calculating the amount of change, the idea that the amount of change is important in potential energy and that only the amount of change has meaning has been established. Even if the calculation through amount of change is successful, it does not guarantee that it does not have any energy value. The reason is that even if the energy has an own value, it still succeeds in explaining the problem by calculating the change. U=mgh, U=-GMm/r : Both give the correct values in the change calculation problem. 4. Regarding gravitational potential energy, some physicists think differently than you. I've talked a lot about potential energy, but the notion acquired by education is strong, and I'm not capable enough to break it. So, a little bit of other people's opinions. 1) Alan Guth said The energy of a gravitational field is negative! The positive energy of the false vacuum was compensated by the negative energy of gravity. 2) Stephen Hawking also said The matter in the universe is made out of positive energy. However, the matter is all attracting itself by gravity. Two pieces of matter that are close to each other have less energy than the same two pieces a long way apart, because you have to expend energy to separate them against the gravitational force that is pulling them together. Thus, in a sense, the gravitational field has negative energy. In the case of a universe that is approximately uniform in space, one can show that this negative gravitational energy exactly cancels the positive energy represented by the matter. So the total energy of the universe is zero. 3) Gravitation and Spacetime (Book) : 25~29P Different forms of energy as source of gravity : Gravitational energy in Earth If we want to discover whether gravity gravitates, we must examine the behavior of large masses, of planetary size, with significant and calculable amounts of gravitational self-energy. Treating the Earth as a continuous, classical mass distribution (with no gravitational self-energy in the elementary, subatomic particles), we find that its gravitational self-energy is about 4.6×10^−10 times its rest-mass energy. The gravitational self-energy of the Moon is smaller, only about 0.2 × 10^−10 times its rest-mass energy. 4) Explanation of GRAVITY PROBE B team https://einstein.stanford.edu/content/relativity/a11278.html Do gravitational fields produce their own gravity? Yes. A gravitational field contains energy just like electromagnetic fields do. This energy also produces its own gravity, and this means that unlike all other fields, gravity can interact with itself and is not 'neutral'. The energy locked up in the gravitational field of the earth is about equal to the mass of Mount Everest, so that for most applications, you do not have to worry about this 'self-interaction' of gravity when you calculate how other bodies move in the earth's gravitational field. i,j, are subscripts used a lot in physics, and are not subscripts used only in the case of Euler coordinates. And, in the symbol of summation, there is also an explanation of gravitational potential energy. So, I don't think anyone interprets it as Euler coordinates. [math] \sum { - \frac{{G{m_i}{m_j}}}{{{r_{ij}}}}} [/math] When obtaining the potential energy of the mass system, the potential terms of all pairs are summed using the summation symbol. Then, since overlapping terms occur, i<j or a<b is used. It is used to avoid overlapping ordered pairs in ordered pairs. In the major books I used, the notation "m_0" was always used to indicate rest mass. The same notation can be seen in the display of the wiki you linked to. When I use a rest mass, I use the notation m_0. The "m" I used is total mass, or equivalent mass. [math]{E^2} = {({m_0}{c^2})^2} + {(pc)^2}[/math]
-
One of humanity's ultimate questions is "How did the universe come into existence?" Since energy is one of the most fundamental physical quantities in physics, and particles and the like can be created from this energy, this question is "How did energy come into existence?" It is related to the question you are asking. Cosmology can be largely divided into a model in which energy has continued to exist and a model in which energy is also created. Each model has its strengths and weaknesses, but in the model that assumes the existence of some energy before the birth of our universe, "How did that energy come into existence?" Since the question still exists, the problem has not been resolved and, therefore, I do not personally prefer it. In order to explain the source of energy in our universe, there have been models that claim the birth of the universe from nothing, or a Zero Energy Universe. However, the key point, the specific mechanism of how being was born from nothing, is lacking, presupposes an antecedent existence such as the Inflaton Field, or is described in a very poor state. *The nothing mentioned here is not a complete nothing, but a state of zero energy. I would like to suggest a solution to this ultimate problem. 1. Changes in the range of gravitational interactions over time In Figure 1, if the mass-energy within the radius R_1 interacted gravitationally at t_1 (an arbitrary early time), the mass-energy within the radius R_2 will interact gravitationally at a later time t_2. As the universe ages, the mass-energy involved in gravitational interactions changes, resulting in changes in the energy composition of the universe. The total energy $E_{T}$ of the system is a [math] {E_T} = \sum\limits_i {{m_i}{c^2}} + \sum\limits_{i < j} { - \frac{{G{m_i}{m_j}}}{{{r_{ij}}}}} = M{c^2} - \frac{3}{5}\frac{{G{M^2}}}{R} [/math] b <math> {E_T} = \sum\limits_i {{m_i}{c^2}} + \sum\limits_{i < j} { - \frac{{G{m_i}{m_j}}}{{{r_{ij}}}}} = M{c^2} - \frac{3}{5}\frac{{G{M^2}}}{R} </math> c [tex] {E_T} = \sum\limits_i {{m_i}{c^2}} + \sum\limits_{i < j} { - \frac{{G{m_i}{m_j}}}{{{r_{ij}}}}} = M{c^2} - \frac{3}{5}\frac{{G{M^2}}}{R} [/tex] Since there is an attractive component (Mass-energy) and a repulsive component (Gravitational potential energy or Gravitational self-energy), it contains elements that can explain the accelerated expansion and decelerated expansion of the universe. In the case of a uniform distribution, comparing the magnitudes of mass energy and gravitational potential energy, it is in the form of -kR^2. That is, as the gravitational interaction radius increases, the negative gravitational potential energy value becomes larger than the positive mass energy. 2. The inflection point at which the magnitudes of mass energy and gravitational potential energy are equal The inflection point is the transition from decelerated expansion to accelerated expansion. If R < R_gs , then the positive mass-energy is greater than the negative gravitational potential energy, so the universe is dominated by attractive force and is decelerating. If R > R_gs, then the negative gravitational potential energy is greater than the positive mass-energy, so the universe is dominated by the repulsive (anti-gravity) force and accelerated expansion. Therefore, by matching R_gs with the time of accelerated expansion in the early universe, we can create a new inflation model. 3. When entering accelerated expansion within the Planck time This means that, in Planck time, a universe born with an energy density of ρ_0 passes through an inflection point where positive energy and negative gravitational potential energy (gravitational self-energy) become equal. And, it means entering a period of accelerated expansion afterwards. 4. Birth and Expansion of the Universe from the Uncertainty Principle 4.1 The Uncertainty Principle - Inflating in Planck time During Planck time, fluctuations in energy During Planck time, energy fluctuation of ΔE=(1/2)m_pc^2 is possible. However, when the mass distribution of an object is approximated in the form of a spherical mass distribution, Δx from the uncertainty principle corresponds to the diameter, not the radius. So Δx=2R'=cΔt, this should apply. In this case, from the values obtained above in "When entering accelerated expansion within the Planck time", the density is quadrupled, the radius is 1/2 times, and thus the mass is (1/2) times. Therefore, the mass value is M'=(5/6)m_p It means, If Δt occurs during the Planck time t_p, the energy fluctuation ΔE can occur more than (1/2)m_pc^2. And, the energy of the inflection point where the mass distribution enters accelerated expansion is (5/6)m_pc^2. In short, According to the uncertainty principle, it is possible to change (or create) more than (1/2)m_pc^2 energy during the Planck time, If an energy change above (5/6)m_pc^2 that is slightly larger than the minimum value occurs, the total energy of the mass-energy distribution reaches negative energy, i.e., the negative mass state, within the time Δt where quantum fluctuations can exist. However, since there is a repulsive gravitational effect between negative masses, the corresponding mass distribution expands instead of contracting. Thus, the quantum fluctuations generated by the uncertainty principle cannot return to nothing, but can expand and create the present universe. 4.2. The magnitude at which the minimum energy generated by the uncertainty principle equals the minimum energy required for accelerated expansion In the above analysis, the minimum energy of quantum fluctuation possible during Planck time is ΔE≥(1/2)m_pc^2, and the minimum energy fluctuation for which expansion after birth can occur is ΔE≥(5/6)m_pc^2. Since (5/6)m_pc^2 is greater than (1/2)m_pc^2, the birth and coming into existence of the universe in Planck time is a probabilistic event. For those unsatisfied with probabilistic event, consider the case where the birth of the universe was an inevitable event. Letting Δt=kt_p, and doing some calculations, we get the k=(3/5)^(1/2) To summarize, If Δt ≤ ((3/5)^(1/2))t_p, then ΔE ≥ ((5/12)^(1/2))m_pc^2 is possible. And, the minimum magnitude at which the energy distribution reaches a negative energy state by gravitational interaction within Δt is ΔE=((5/12)^(1/2))m_pc^2. Thus, when Δt < ((3/5)^(1/2))t_p, a state is reached in which the total energy is negative within Δt. In other words, when quantum fluctuation occur where Δt is smaller than (3/5)^(1/2)t_P = 0.77t_p, the corresponding mass distribution reaches a state in which negative gravitational potential energy exceeds positive mass energy within Δt. Therefore, it can expand without disappearing. In this case, the situation in which the universe expands after birth becomes an inevitable event. [Abstract] There was a model claiming the birth of the universe from nothing, but the specific mechanism for the birth and expansion of the universe was very poor. According to the energy-time uncertainty principle, during Δt, an energy fluctuation of ΔE is possible, but this energy fluctuation should have reverted back to nothing. By the way, there is also a gravitational interaction during the time of Δt, and if the negative gravitational self-energy exceeds the positive mass-energy during this Δt, the total energy of the corresponding mass distribution becomes negative energy, that is, the negative mass state. Because there is a repulsive gravitational effect between negative masses, this mass distribution expands. Thus, it is possible to create an expansion that does not go back to nothing. Calculations show that if the quantum fluctuation occur for a time less than Δt = ((3/10)^(1/2))t_p ~ 0.77t_p, then an energy fluctuation of ΔE > ((5/6}^(1/2))m_pc^2 ~ 0.65m_pc^2 must occur. But in this case, because of the negative gravitational self-energy, ΔE will enter the negative energy (mass) state before the time of Δt. Because there is a repulsive gravitational effect between negative masses, ΔE cannot contract, but expands. Thus, the universe does not return to nothing, but can exist. Gravitational Potential Energy Model provides a means of distinguishing whether the existence of the present universe is an inevitable event or an event with a very low probability. And, it presents a new model for the process of inflation, the accelerating expansion of the early universe. This mechanism also provides an explanation for why the early universe started out in a high dense state. Additionally, when the negative gravitational potential energy exceeds the positive mass energy, it can produce an accelerated expansion of the universe. Through this mechanism, inflation, which is the accelerated expansion of the early universe, and dark energy, which is the cause of the accelerated expansion of the recent universe, can be explained at the same time. * The above is a summary of some of the key arguments of the paper, and for more details, please refer to the paper linked below. # The Birth Mechanism of the Universe from Nothing and New Inflation Mechanism https://www.researchgate.net/publication/371951438 # Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field https://www.researchgate.net/publication/360096238