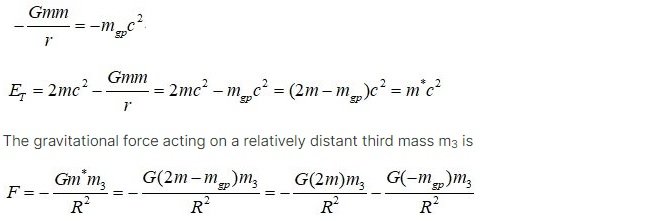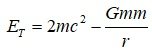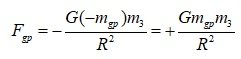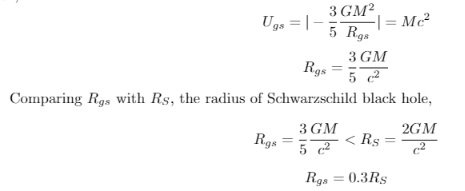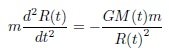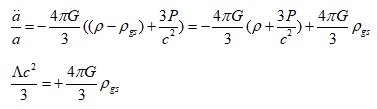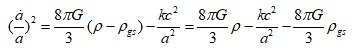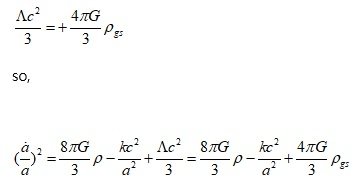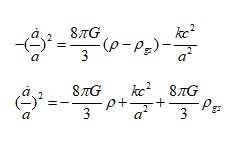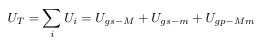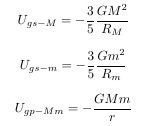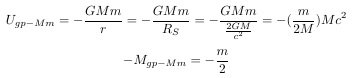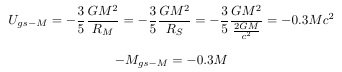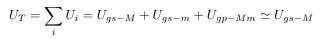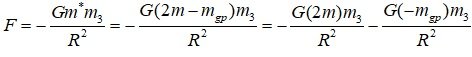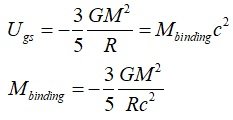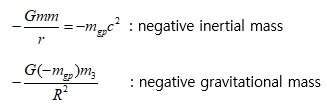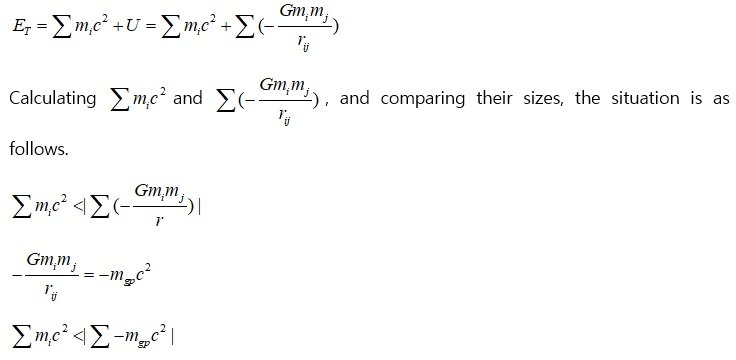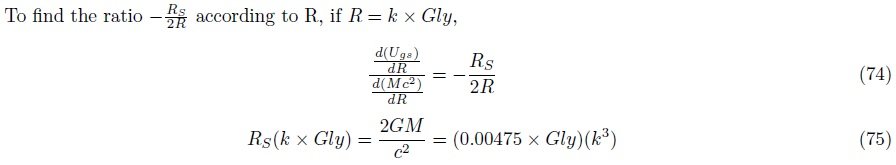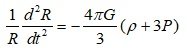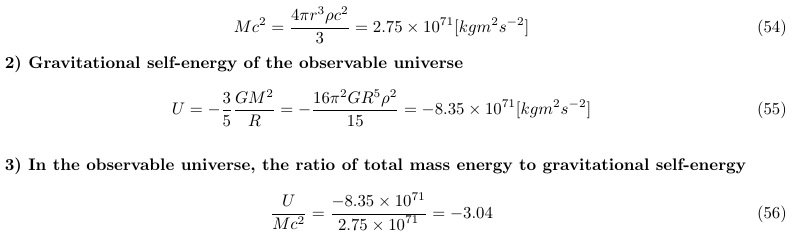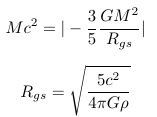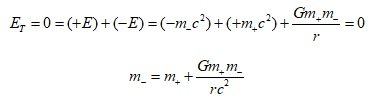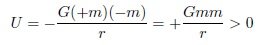icarus2

It's same the expression on the wiki. Since I only talked about the dark energy term in some equations, I omitted the notation a little, so there seems to be a misunderstanding. Since vacuum energy or cosmological constant can also be expressed in terms of mass density [math]{\rho _\Lambda }[/math] and pressure [math]{P_\Lambda }[/math], standard cosmology introduces, So~ [math] \frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right) [/math] stands for [math]\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {{\rho _m} + {\rho _{rel}} + {\rho _\Lambda } + \frac{{3({P_m} + {P_{rel}} + {P_\Lambda })}}{{{c^2}}}} \right)[/math] From the equation including the cosmological constant on the wiki, [math]\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right) + \frac{{\Lambda {c^2}}}{3} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}} - \frac{{\Lambda {c^2}}}{{4\pi G}}} \right)[/math] If we express each component including, [math]\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}} - \frac{{\Lambda {c^2}}}{{4\pi G}}} \right) = - \frac{{4\pi G}}{3}\left( {{\rho _m} + {\rho _{rel}} + {\rho _\Lambda } + \frac{{3({P_m} + {P_{rel}} + {P_\Lambda })}}{{{c^2}}}} \right) [/math] Therefore, in the standard cosmology?, the dark energy term holds the following relation. [math] - \frac{{\Lambda {c^2}}}{{4\pi G}} = {\rho _\Lambda } + \frac{{3{P_\Lambda }}}{{{c^2}}} [/math] Standard cosmology or mainstream cosmology defines [math] \rho _\Lambda [/math] as [math] {\rho _\Lambda } \equiv \frac{{\Lambda {c^2}}}{{8\pi G}} [/math] [math] {P_\Lambda } = - {\rho _\Lambda }{c^2} = - \frac{{\Lambda {c^4}}}{{8\pi G}} [/math] [math] - \frac{{\Lambda {c^2}}}{{4\pi G}} = \frac{{\Lambda {c^2}}}{{8\pi G}} + \frac{{3( - \frac{{\Lambda {c^2}}}{{8\pi G}}{c^2})}}{{{c^2}}} = \frac{{\Lambda {c^2}}}{{8\pi G}} - \frac{{3\Lambda {c^2}}}{{8\pi G}} = - 2(\frac{{\Lambda {c^2}}}{{8\pi G}}) = - 2{\rho _\Lambda }[/math] If C=1 is set, [math] - \frac{{\Lambda {c^2}}}{{4\pi G}} = {\rho _\Lambda } + \frac{{3{P_\Lambda }}}{{{c^2}}} [/math] [math] - 2{\rho _\Lambda } = {\rho _\Lambda } + 3{P_\Lambda } = {\rho _\Lambda } + 3( - {\rho _\Lambda }) = - 2{\rho _\Lambda }[/math] In this article, I am only talking about the dark energy term, and point out the problem with the core logic of dark energy. So, I used this expression to simply express only the core. [math] \rho + 3P = \rho + 3( - \rho ) = - 2\rho [/math] The mainstream argument for dark energy is that it has a positive energy density [math]+\rho _\Lambda [/math] , a negative pressure, that is, a negative kinetic energy component [math]-3\rho _\Lambda [/math], and finally a mass density of [math]-2\rho _\Lambda [/math]. Another result of standard cosmology [math] \frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {{\rho _m} + {\rho _{rel}} + {\rho _\Lambda } + \frac{{3({P_m} + {P_{rel}} + {P_\Lambda })}}{{{c^2}}}} \right) [/math] For simple analysis, applying c=1, [math] {\rho _{rel}} + \frac{{3{P_{rel}}}}{{{c^2}}} < < {\rho _m} [/math], [math]\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {{\rho _m} + {\rho _\Lambda } + 3{P_\Lambda }} \right)[/math] Current standard cosmology is, approximately [math] {\rho _m} \sim 31.7\% ,{\rho _\Lambda } \sim 68.3\% [/math] ([math]\rho _m[/math] is matter + dark matter) [math]{\rho _m} \sim \frac{1}{3}{\rho _c}[/math] [math]{\rho _\Lambda } \sim \frac{2}{3}{\rho _c}[/math] [math]{\rho _m} + {\rho _\Lambda } + 3{P_\Lambda } = \frac{1}{3}{\rho _c} + \frac{2}{3}{\rho _c} + 3( - \frac{2}{3}{\rho _c}) = - {\rho _c}[/math] Consequently, the result of standard cosmology is that the universe has a negative mass density [math] - {\rho _c}[/math] . The current state of the universe is a form in which negative mass (density) twice that of positive mass exists. Since the negative mass density conflicts with their notion, they do not talk about the final result, but only talk about the slightly vague negative pressure and stop. People say: Dark energy has a positive energy density and acts as a negative pressure. So, the accelerated expansion of the universe is explained. Wow!, problem solved. They call it "standard cosmology" as they like~ The introduction of negative pressure did not solve or explain the problem. It just feels like it's been solved. The introduced negative pressure conflicts with existing physics. (Existences with positive energy density and negative kinetic energy, super-luminous speed, imaginary speed~, whether dU=-PdV is applicable to a situation in which energy is not conserved, Minor error of 10^120...) No. I'm saying that even if vacuum energy (with [math] \rho _\Lambda [/math]) exists, it has no negative pressure. Therefore, the current mainstream model is wrong. And, gravitational potential energy or gravitational field's energy seems to be the source of dark energy.

Pressure P = equivalent energy density of kinetic energy P/c^2 = equivalent mass density of kinetic energy So, in the Book(An Introduction to Modern Astrophysics 1161P) say that equivalent mass (density) of the particle's kinetic energy... When a new phenomenon is discovered, we try to explain the new phenomenon within the existing theoretical framework. The current negative pressure is also a problem caused by trying to explain within the existing theoretical framework. The current cosmology is based on general relativity, among them, the 1915 field equation without cosmological constant and the field equation with cosmological constant in particular. For the universe to accelerating expansion, the right side of Friedmann's equation must be positive, and therefore (p+3P)<0. So, the researchers came up with the following logic: p+3P=p+3(-p)=-2p However, as raised in the main text, p+3P=p+3(-p)=-2p has serious problems and contradicts existing physics. In my opinion, Positive energy density and negative kinetic energy are logically contradictory. Moreover, p+3P=p+3(-p)=-2p It seems impossible for a physical existence that satisfies this relational expression. Nothing seems to have a kinetic energy component that is three times greater than that of light. Even if vacuum energy with positive energy density p exists, the pressure P created by that vacuum energy is estimated to have a positive pressure of 0~(1/3)p. So, even if vacuum energy with positive energy density exists, it cannot create negative pressure. There is no negative pressure, instead there is a negative gravitational potential energy by a positive energy density. So how do you create a negative pressure component, that is, a repulsive force component? After all, the root of the problem is Einstein's 1915 field equation. Einstein's field equation was a huge success in weak gravitational field. However, there is a problem in strong gravitational field where the energy of the gravitational field must be taken into account. The singularity problem is strong evidence that Einstein's field equation is incomplete. 1. The fundamental principle of general relativity states that “all energy is a source of gravity”. However, the field equation created by Einstein did not fully realize this principle The energy of the gravitational field must also function as a gravity source. Einstein was also aware of this, and for over two years, beginning in 1913, he worked to formulate a field equation that included the energy-momentum of the gravitational field. However, because it was difficult to define the energy-momentum tensor of the gravitational field in general relativity, Einstein could not complete the field equation including the gravitational action of the gravitational field. So, we have a field equation involving only the energy-momentum tensor of matter. Because of the omission of the energy-momentum of the gravitational field, the singularity problem and the dark energy problem came into existence. 1)Gravitation and Spacetime (Book) 2)Explanation of GRAVITY PROBE B team 2. As the mass increases, the ratio of negative gravitational potential energy to mass energy increases Wikipedia, Gravitational binding energy When two masses m are separated by a distance r, ● —- r —- ● The total energy of the two particle systems is In the dimension analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of (mass) x (speed)^2. So, E=mc^2 (Here, m is not used as a word for rest mass) holds true for all kinds of energy. If we introduce the equivalent mass -m_gp for the gravitational potential energy, That is, when considering the gravitational action of a bound system, not only the mass in its free state but also the binding energy term (negative gravitational potential energy) should be considered. Look at the second term, the repulsive gravitational force term. In general, gravitational self-energy is small compared to the mass energy, but as the mass increases, the ratio of negative gravitational potential energy to mass energy increases. -M_gs = Equivalent mass of total gravitational potential energy (gravitational self-energy) of an object. Mass energy is proportional to M, whereas the gravitational self-energy is proportional to -M^2/R. Moon’s -M_gs = (-2.0 x 10^-11)M_Moon Earth's -M_gs = (- 4.17 x 10^-10)M_Earth Sun's -M_gs = (- 1.27 x 10^-4)M_Sun Black hole's -M_gs = (- 3 x 10^-1)M_Black-hole *In the case of the Earth, the Sun and the Black hole, please do your own calculations. Then you will notice that this value increases considerably. It can be seen that as the mass increases, the ratio of negative gravitational self-energy to mass energy increases. Therefore, as the mass increases, the gravitational action of the gravitational field must be taken into account. Since mass energy is proportional to M, whereas gravitational self-energy is proportional to -M^2/R, the greater the mass, the greater the proportion of negative gravitational self-energy. So, now the question we have to ask is, "What value would the negative gravitational potential energy in the case of a universe with a greater mass?" 3. In the universe, if we calculate the gravitational self-energy or total gravitational potential energy The universe is almost flat, and its mass density is also very low. Thus, Newtonian mechanics approximation can be applied. Since the particle horizon is the range of interaction, if we find the Mass energy (Mc^2) and Gravitational self-energy ((-M_gs)c^2) values at each particle horizon, Mass energy is an attractive component, and the equivalent mass of gravitational self-energy is a repulsive component. Critical density value p_c = 8.50 x 10^-27[kgm^-3] was used. At particle horizon R=16.7Gly, (-M_gs)c^2 = (-0.39M)c^2 : |(-M_gs)c^2| < (Mc^2) : Decelerated expansion period At particle horizon R=26.2Gly, (-M_gs)c^2 = (-1.00M)c^2 : |(-M_gs)c^2| = (Mc^2) : Inflection point (About 5-7 billion years ago, consistent with standard cosmology.) At particle horizon R=46.5Gly, (-M_gs)c^2 = (-3.04M)c^2 : |(-M_gs)c^2| > (Mc^2) : Accelerated expansion period Even in the universe, gravitational potential energy (or gravitational field’s energy) must be considered. And, in fact, if we calculate the value, since gravitational potential energy is larger than mass energy, so the universe has accelerated expansion. Gravitational potential energy accounts for decelerated expansion, inflection point, and accelerated expansion. If we could create a new field equation that perfectly reflects the principle(All energy is a source of gravity, so, the energy of the gravitational field is also a source of gravity) of general relativity and find a solution to it, the dark energy problem will be solved. The model of Gravitational Potential Energy 1) has a clear origin, 2) is a physical quantity required by the principle of general relativity, 3) has decelerated expansion, inflection point, and accelerated expansion period, 4) does not require fine-tuning, 5) does not have the problem of coincidence, 6) Since dark energy term is presented as a function of time, it is verifiable. Λ(t) = (6πGR(t)ρ(t)/5c^2)^2 https://www.researchgate.net/publication/360096238_Dark_Energy_is_Gravitational_Potential_Energy_or_Energy_of_the_Gravitational_Field

From the second Friedmann equation or acceleration equation, [math] \frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - (\frac{{4\pi G}}{3})(\rho + 3P)[/math] Since ρ is the mass density in the acceleration equation, the pressure term P has a dimension of energy density (c=1). Current acceleration equation inevitably require negative mass density. Without negative (gravitational) mass density, it is impossible to create acceleration expansion. The mainstream produces acceleration expansion by setting the pressure of the cosmological constant or vacuum energy to P=−ρ . Currently, dark energy is described as a being that exerts a negative pressure while having a positive energy density. However, there is a serious problem when considering a physical existence with these characteristics. ρ+3P=ρ+3(−ρ)=−2ρ 1) Sign of the negative pressure Since the universe is treated as a fluid with uniform density, the pressure between regions is zero. In general relativity, pressure is equivalent energy density of the kinetic energy. In the acceleration equation, 3P has the idea of an equivalent energy density corresponding to the kinetic energy of the particle. So, assuming that the pressure P term has a negative energy density is same assuming that it has negative kinetic energy. In order to have negative kinetic energy, it must have negative inertial mass or imaginary velocity. But, because they assumed a positive inertial mass, it is a logical contradiction. [math]K = \frac{1}{2}m{v^2} < 0[/math] m<0 or v=Vi : negative mass or imaginary speed. Negative mass contradicts the assumption of positive energy density, and energy density with imaginary speed is far from physical reality. 2) Size of the negative pressure In the ideal gas state equation, we obtain, [math]P = \frac{1}{3}(\frac{{{v^2}}}{{{c^2}}})\rho = \omega \rho[/math] In the case of matter, v << c, So [math]P = \frac{1}{3}{(\frac{v}{c})^2}\rho \simeq 0[/math] In the case of radiation, v=c, So [math]P = \frac{1}{3}{(\frac{v}{c})^2}\rho = \frac{1}{3}\rho [/math] However, in the case of dark energy [math]P = \frac{1}{3}{(\frac{v}{c})^2}\rho = - \rho [/math] a) Only considering the size (absolute value) [math]P = \frac{1}{3}{(\frac{v}{c})^2}\rho = | - \rho |[/math] [math]v = \sqrt 3 c[/math] We need energy density with super-luminous speed.(FTL) b) Considering even the negative sign [math]P = \frac{1}{3}{(\frac{v}{c})^2}\rho = - \rho[/math] [math]v = (\sqrt 3 c)i[/math] We need energy density with imaginary super-luminous speed. We can avoid this problem by assuming that cosmological constant or vacuum energy does not apply to the results (ideal gas state eq.) obtained through physics. However, ideal gas state equation applies to "massless ~ infinite mass'' particles, and the velocity ranges from "0 ~ c'' are all included. If we seriously consider the physical presence of P=-p=-3(p/3), we will find that there is a serious problem. 3) Incorrect application of dU = - PdV In the equation dU = - PdV, researchers claim that negative pressure exists if the energy density remains constant as the volume increases. Is this claim correct? Going to the root of the problem, the analysis of this formula seemed simple (dU=pdV), so I had the illusion that the logic of negative pressure was certain. But~ a) This explanation is an inverted explanation Since pressure is a property of an object, pressure exists first, and because of this pressure, changes in internal energy according to volume change appear. That is, since pressure is positive, if dV>0, then dU<0. Since the pressure is positive, if dV<0, then dU>0. By the way, we use the logic "if dV>0, dU>0, then P<0''. How are you sure that this logic is correct? b) ρ+3P=ρ+3(−ρ)=−2ρ Mass density ρ and pressure P are properties of the object to be analyzed. Both mass density ρ and pressure P are sources of gravity. It means that even if the region maintains a constant size without expanding or contracting, gravitational force is applied as much as ρ+3P . In other words, it suggests that the object (or energy density) has a gravity with a negative mass density of −2ρ . This is different from a vacuum with a positive energy density ρ , which we think of. c) dU = - PdV is the expression obtained when the law of conservation of energy is established dU=dQ-dW, if dQ=0, dU=-dW=-PdV However, in the case of vacuum energy and the cosmological constant, energy conservation does not hold. As the universe expands, the total energy in the system increases. Therefore, we cannot guarantee that dU = - PdV holds. dU = - PdV is an equation that holds when the energy of the system is conserved. However, researchers are applying this equation to vacuum energy or cosmological constant where the energy of the system is not conserved. "In the equation dU = - PdV, even if the universe expands, if it has a uniform density, it should have a negative pressure...'' What's wrong here? I am not sure if this equation holds even for negative pressure. However, although this equation holds even in the case of negative pressure, its interpretation is as follows. This equation holds true when substances in radius r_1 expand from r_1 to r_2 (r_2 > r_1), and have the same uniform density in r_1 and r_2. In other words, it is argued that a negative pressure is required to create a uniform density effect only with the material present in radius r_1. But, vacuum energy is a form in which energy is newly generated by an increased volume. It is also energy that can be assumed to have an initial speed of 0 ~ c. Considering the positive energy density, pressure term seems reasonable to assume 0 ~ (1/3)p. If the cosmological constant term is shifted to the right side of the field equation, it becomes a negative equivalent mass. It is not an object that has a positive energy density (positive inertial mass) and acts on a negative gravitational mass, but just a negative mass. It is not necessary for an entity to exist that exerts a negative pressure while having a positive energy density. Only a negative mass component may exist, or a positive energy component may exist and a negative energy component may exist. And, the negative energy component may be the energy of the gravitational field or the gravitational potential energy. Q1. Is it possible to have negative kinetic energy while having positive mass density? Is it possible for a physical entity to have an imaginary velocity while having a positive energy density? Q2. [math]P = - \rho = - 3(\frac{1}{3}\rho ) [/math] Can such an entity (an entity with a pressure(kinetic energy component) three times greater than light) physically exist? Q3. Is dark energy energy with FTL (Faster Than Light) or an imaginary FTL? Q4. Does the dU=-PdV equation hold for a system in which energy is not conserved? Q5. Even if the universe expands, If an entity with uniform mass (energy) density exists, it is said that it will have a negative pressure. Is this claim correct? We can considered the vacuum energy density with P=0. However, in order to have a uniform energy density even when space expands, does it have to suddenly have negative pressure? Shouldn't it be newly created, with P=0, and filling the larger universe? Can we not think of a vacuum energy density with P=0? Can't there be a vacuum energy density with P=0 ~ (1/3)p? Even if vacuum energy is present, it is not certain whether it creates a negative pressure. ρ+3P=ρ+3(−ρ)=−2ρ There seems to be a serious problem with this argument.

\( y=x^2 \) [math] y = x^2 [/math] $K = \frac{1}{2}m{v^2} $ [math]K = \frac{1}{2}m{v^2} [/math]

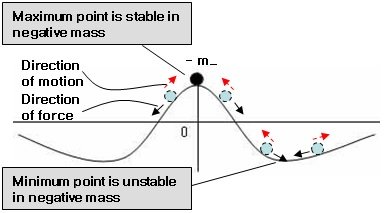
I am a person working on negative mass. I'm not a pro, but I think my research will contain some useful information for you. The negative mass I studied is a particle with both inertial and gravitational masses having negative values. In 2009 and 2012, I wrote papers explaining dark matter and dark energy through negative mass. Hypothesis of dark matter and dark energy with negative mass https://www.researchgate.net/publication/228610043 Is the State of Low Energy Stable Negative Energy Dark Energy and Dark Matter https://www.researchgate.net/publication/263468413 After that, I did some more research, Introduce at least 2 papers and 1 video that you should read, 1)On Problems and Solutions of General Relativity https://www.researchgate.net/publication/286935998 2) Dark Matter is Negative Mass https://www.researchgate.net/publication/324525352 3)Is the State of Low Energy Stable? Negative Mass and Negative Energy https://www.youtube.com/watch?v=MZtS7cBMIc4 The above papers contain contents related to the errors of mainstream academics related to negative mass. False claims or misconceptions about negative mass 1) The vacuum instability problem is wrong. 2) The runaway motion problem is wrong. 3) Perpetual motion problem(Wheel problem with negative and positive mass) is wrong. So, if you are interested in negative mass, I think the above 2 papers and 1 video will be helpful.

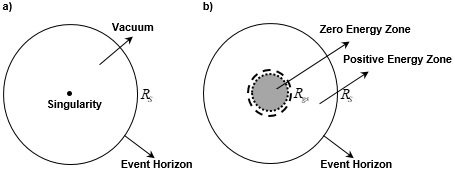
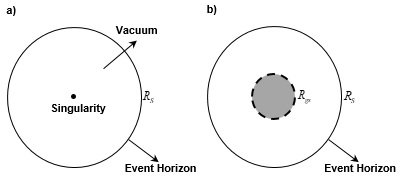
5. Internal structure of black hole considering gravitational self-energy (p10~) Fig-x. Internal structure of the black hole. a)Existing model b)New model. If, over time, the black hole stabilizes, the black hole does not have a singularity in the center, but it has a Zero (total) Energy Zone. When the mass distribution inside the black hole is reduced from R_S to R_{gs} (or R_{gs - vir}), the energy must be released from the inside of the system to the outside of the system in order to reach this binding state. Here, the system refers to the mass distribution within the radius 0 ≤ r ≤ R_gs (or R_{gs - vir}). Although potential energy changes to kinetic energy, in order to achieve a stable bonded state, a part of the kinetic energy must be released to the outside of the system. We need to consider the virial theorem. At this time, the emitted energy does not go out of the black hole. This energy is distributed in the R_{gs} (or R_{gs - vir}) < r ≤ R_S region. If you have only the concept of positive energy, please refer to the following explanation. From the point of view of mass defect, r=R_{gs} (or R_{gs - vir}) is the point where the total energy of the system is zero. For the system to compress more than this point, there must be an positive energy release from the system. However, since the total energy of the system is zero, there is no positive energy that the system can release. Therefore, the system cannot be more compressed than r=R_{gs} (or R_{gs - vir}). So black hole doesn't have singularity. By locking horns between gravitational self-energy and mass energy, particles inside black hole or distribution of energy can be stabilized. When considering a region within a shell with an arbitrary radius inside a black hole, Since there is a repulsive gravitational effect between negative masses, the region within R_shell expands again when it enters the negative mass state. This will cause the area within the R_shell to expand until it has a positive mass state. Therefore, over time, a Zero Energy Zone with zero total energy will be established at the center of the black hole. As a final state, the black hole does not have a singularity in the center, but it has a Zero (total) Energy Zone (ZEZ). R_gs is the maximum of ZEZ. And, this gravitational self-energy can solve the fatal flaws of Black Hole Cosmology and save the Black Hole Cosmology or Black Hole Universe. 6. Inside a large enough black hole, there is enough space for intelligent life to exist (P11~) A black hole has no singularity, has a Zero Energy Zone with a total energy of zero, and this region is very large, reaching 15% ~ 30% of the radius of the black hole. It suggests an internal structure of a black hole that is completely different from the existing model. Inside the huge black hole, there is an area where intelligent life can live. This size is approximately 30% of the radius of the black hole. Even the smallest stellar black hole is 3 km in size. In the case of a black hole 100 million times the size of the Sun, its size is 3x10^8 km. Under the observed average density, the size of Universe Black Hole and Zero Energy Zone. If the size of the mass distribution increases R times, the Universe Black Hole and ZEZ created by the new mass distribution become R^3 times larger. Therefore, by considering gravitational self-energy, it is possible to solve the problem of singularity of black hole, which is the most important problem in general relativity. And, this discovery provides a logic for why we are surviving in universe black hole (formed when only mass energy is considered) without collapsing into singularity. *It varies slightly depending on the average density (or critical density) value used. For example, if the masses are distributed approximately 46.5Gly with the average density of the current universe, the size of the black hole created by this mass distribution will be 491.6Gly, and the size of the Zero Energy Zone will be approximately 73.7Gly ~ 147.5Gly. In other words, there is no strong tidal force and a region with almost flat space-time that can form a stable galaxy structure is much larger than the observable range of 46.5Gly. The entire universe is estimated to be much larger than the observable universe, so it may not be at all unusual for us to observe only the Zero Energy Zone (nearly flat space-time). Even if humans live inside a black hole called the universe, a sufficiently stable survival area for intelligent life is guaranteed. The gravitational self-energy (or gravitational potential energy) prevents the universe from collapsing into a singularity, provides enough space (approximately 0.3R_s) for intelligent life, and ensures a near-flat space-time (Zero Energy Zone). # On the solution of the strong gravitational field the solution of the Singularity problem the origin of Dark energy and Dark matter (10~11P) # Problems and Solutions of Black Hole Cosmology

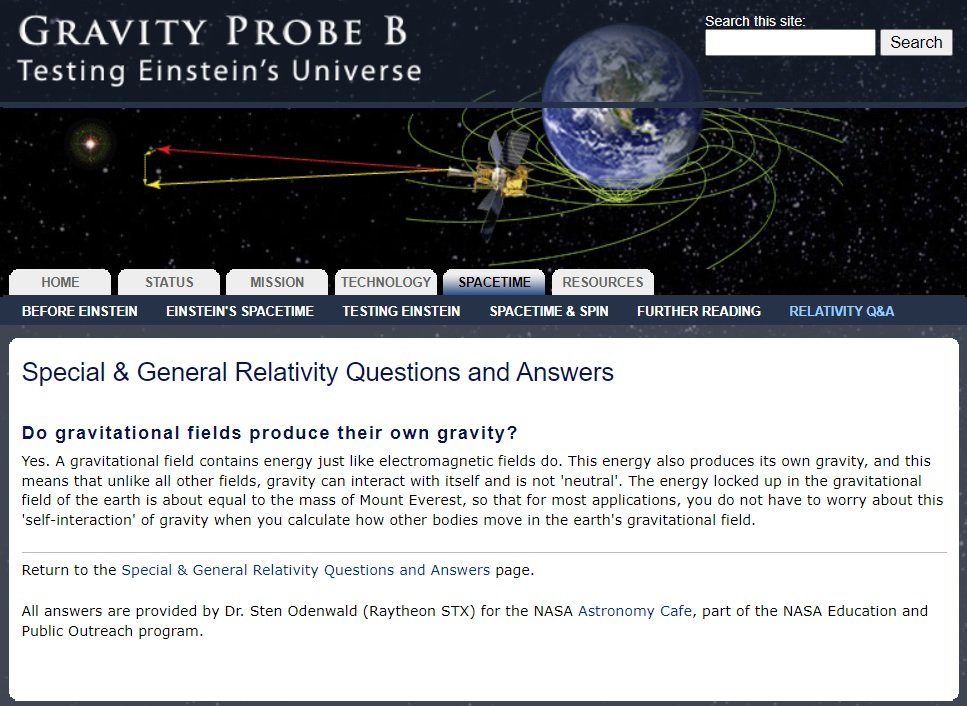
Many people think that the singularity problem can be solved in the quantum mechanics range, but this may be a wrong estimate. If you (This means the person reading this article) calculate the mass defect due to binding energy, gravitational potential energy, and gravitational self-energy, you have a different idea. Mass defects are a proven fact. Now we need to ask a question about the following situation. d), e) What happens when the distance gets closer and closer to a distance that can cancel out the mass energy? If we calculate the gravitational self-energy of the object, The greater the mass, the greater the gravitational self-energy ratio. Earth's -Mgs = (- 4.17x10-10)M_Earth Sun's -Mgs = (- 1.27x10-4)M_Sun Black hole's -Mgs = (- 0.3)M_black-hole at R=R_s=2GM/c^2, U_gs=-(3/5)GM^2/R = -(3/5)GM^2/(2GM/c^2) = -0.3Mc^2 And now, If we calculate the magnitude at which gravitational self-energy equals mass energy, That is, the singularity problem disappears at 0.3R_s. This size is approximately 30% of the radius of the black hole. Even the smallest stellar black hole is about 3km in size. In the case of a black hole 100 million times the size of the Sun, its size is 1x10^8 km. Gravity can solve the gravitational singularity problem without entering the realm of quantum mechanics. It is also known that Einstein, since 1913, tried to formulate an equation that takes into account the gravitational action of the gravitational field. He studied for two years, but could not come up with an equation considering the gravitational action of the gravitational field, and ultimately became the current field equation. It seems necessary to examine whether the 1915 field equation came out because he could not establish an appropriate equation considering the energy-momentum of the gravitational field, or whether it came out because he thought the 1915 field equation was in the correct form. All energy is a source of gravity. Gravitational potential energy is also a source of gravity. 1) Gravitational and Spacetime -Book 2) Explanation of GRAVITY PROBE B https://einstein.stanford.edu/conten...ty/a11278.html Do gravitational fields produce their own gravity? Yes. A gravitational field contains energy just like electromagnetic fields do. This energy also produces its own gravity, and this means that unlike all other fields, gravity can interact with itself and is not 'neutral'. The energy locked up in the gravitational field of the earth is about equal to the mass of Mount Everest, so that for most applications, you do not have to worry about this 'self-interaction' of gravity when you calculate how other bodies move in the earth's gravitational field. 3) https://en.wikipedia.org/wiki/Gravitational_binding_energy Negative mass component[edit] Two bodies, placed at the distance R from each other and reciprocally not moving, exert a gravitational force on a third body slightly smaller when R is small. This can be seen as a negative mass component of the system, equal, for uniformly spherical solutions, to: For example, the fact that Earth is a gravitationally-bound sphere of its current size costs 2.49421×1015 kg of mass (roughly one fourth the mass of Phobos – see above for the same value in Joules), and if its atoms were sparse over an arbitrarily large volume the Earth would weigh its current mass plus 2.49421×1015 kg kilograms (and its gravitational pull over a third body would be accordingly stronger). Gravitational self-energy can solve the singularity problem without entering the realm of quantum mechanics. Dark energy problem and singularity problem can be resolved by the gravitational action of the gravitational field. And, perhaps the dark matter problem is also related to the gravitational action of the gravitational field. In astronomy, the present big problems seem to be due to the inability to complete the field equation including the gravitational action of the gravitational field (a form of equation that everyone agrees on), and even if they did, they could not find a solution to it. So, if you (this means the person reading this article) have the ability, you can solve both the dark energy problem and the singularity problem at the same time if you create a field equation including the gravitational action of the gravitational field and find a solution.

Thanks for your comments and advice. The following post is the personal thoughts of a less knowledgeable person. You are talking about accuracy or perfection. Self-coupling, non-linearity~ However, in my personal opinion, 100% accuracy or perfection is an ideal, not a reality. The basis of current cosmology is Einstein's field equation. So, we have to ask the following question. Is Einstein's field equation perfect? 1. Some scholars, including Hans Ohanian, have made this claim. In writing the field equation (48) we have assumed that the quantity T^{\mu \nu is the energy-momentum tensor of matter. In order to obtain a linear field equation we have left out the effect of the gravitational field upon itself. Because of this omission, our linear field equation has several (related) defects: (1) According to (48) matter acts on the gravitational field (changes the fields), but there is no mutual action of gravitational fields on matter; that is, the gravitational field can acquire energy-momentum from matter, but nevertheless the energy-momentum of matter is conserved (\partial _\nu }{T^{\mu \nu } = 0). This is an inconsistency. (2)Gravitational energy does not act as source of gravitation, in contradiction to the principle of equivalence. Thus, although Eq. (48) may be a fair approximation in the equivalence. Thus, although Eq. (48) may be a fair approximation in the case of weak gravitational fields, it cannot be an exact equation. The obvious way to correct for our sin of omission is to include the energy-momentum tensor of the gravitational field in T^{\mu \nu }. This means that we take for the quantity T^{\mu \nu } the total energy-momentum tensor of matter plus gravitation: T^{\mu \nu }} = T_{(m)}^{\mu \nu } + {t^{\mu \nu } Here T_{(m)}^{\mu \nu } and t^{\mu \nu } are, respectively, the energy-momentum tensor of matter and gravitation. We assume that the interaction energy of matter and gravitation is always included in T_{(m)}^{\mu \nu }; this is a reasonable convention since the interaction energy-density will only differ from zero at those places where there is matter. 2. The singularity problem Is Einstein's field equation perfect? If perfect, there shouldn't have been any singularity issues. Because the field equation predicts an object to which one's own theoretical system cannot be applied~ 3. The magnitude of the error of the field equation suggested by the gravitational self-energy Sun : -M_gs-sun = (- 1.27x10^-4)M_sun Black hole : -M_gs-Black-hole = (-0.3)M_Black hole observable universe : M_gs = (-3.04) M This suggests the possibility of a significant error. Current field equation are known to work well in weak gravitational fields, but have problem in strong gravitational field. And, even if it is not a strong gravitational field, it seems that a problem arises when a lot of material (on a cosmic scale) is collected. Already we are describing problems using approximation rather than perfection. Should we pause until we have a complete field equation that includes the gravitational action of the gravitational field? It's good if it's perfect, and even if it's not perfect, just go one step further. Until the perfect expression comes out~ What makes physics beautiful is approximation. Achieving 100% accuracy requires taking into account a number of complex factors that arise, which often make the problem unsolvable. In this case, the approximation, although not 100%, solves the problem and in some cases also guarantees the necessary degree of accuracy. Approximation can serve to break the Gordian knot. In other words, Whereas a model that attempts to include the gravitational action of a gravitational field fails to yield results because it is attempting to untie the knot, Because I ignorantly swung my sword and made an approximation, I can make predictions about the cosmological constant or dark energy. 4. Gravitational self-energy may be the first, largest and most important term in self-interaction, nonlinearity. In self-coupling, nonlinearity problems The gravitational self-energy may be the first, largest and most important term in self-interaction, nonlinearity. Because it is the first gravitational potential energy term created by mass in infinite self-interaction. So, I applied it directly to the Friedmann model and looked up the expression for the cosmological constant. ============== Since standard cosmology has been established, I have looked up Friedmann's equations to compare them with standard cosmology. I used the existing gravitational self-energy equation, but there are some problems with applying this equation to cosmology. 1) The existing gravitational self-energy equation is an equation obtained by Newtonian mechanics. It does not reflect the general relativistic idea that all energy is a source of gravity. For example, when calculating the gravitational self-energy equation, use M' as the internal mass. At this time, the internal mass M' also has its own gravitational energy value, which contributes as a negative mass. These contents are not reflected. 2) In the universe, there are objects that are strongly bound by gravity, such as stars, black holes, and galaxies. The gravitational self-energy of these objects is already reflected in the total mass of the object (observed from the outside). By the way, the gravitational self-energy equation assumes a uniform distribution and is a structure in which all the gravitational potential energy terms of all infinitesimal mass are added. Therefore, there is a possibility that expression U_gs=-(3/5)GM^2/R overestimates gravitational self-energy. 3) Because of the propagation velocity of the field, it is possible that some matter within the particle horizon is not participating in gravitational interactions That is, it is possible that the gravitational field has not yet been transmitted from one end to the other. There is a possibility of overcalculation of gravitational self-energy. In addition to 1) - 3) mentioned here, there may be factors that need to be corrected. Therefore, β(t) is introduced as a correction term by these factors. The universe structure correction variable β(t) is a variable, but it is thought to change very slowly since the change will be relatively small after the formation of the galactic structure. So, it is assumed that after the formation of the galactic structure, it can be thought of almost like a constant. To see if the derived equation is probable, I calculated the value of the cosmological constant. Existing cosmological constant models are known to have a difference of 10^120 times between the theoretical predicted value and the observed value. In the gravitational self-energy model, excluding the universe structure correction variable β(t), the difference is not even by a factor of 10^1 order. a(t)R is the particle horizon at the point in time to be analyzed. In the gravitational self-energy model, if ρ(t) ~ 1/a(t)R, it is possible that the density of dark energy seems to be constant. However, I think that the density of dark energy will change. In standard cosmology, the energy density of dark energy is a constant. However, in the gravitational self-energy model, dark energy density is a variable. The dark energy (or cosmological constant term) is a function of time. If the above equation holds in the observation, then the gravitational self-energy model is correct or an appropriate approximation. If the above equation does not hold in the observation, the gravitational self-energy model is wrong. The source of dark energy is gravitational self-energy or gravitational potential energy. https://www.researchgate.net/publication/359329109

Friedmann's equations are derived from field equation, but can also be derived from Newtonian mechanics. And, this way seems to suggest that gravitational self-energy has potential. Of course, Newtonian derivation is not accurate. However, can we consider gravitational self-energy? It seems enough to answer this question. Here, internal masses are included in the mass term M, and a spherical mass distribution is assumed. This is a case where gravitational self-energy can be applied. Even when using the FLRW metric, there is a relative distance a(t)R or radius defined by the scale factor a(t), and there is an mass density. If we add a coefficients to the mass(energy) density, it will be restored to the mass in a(t)R. As long as internal masses are applied, the gravitational self-energy between their internal mass terms always seems applicable. Anyway, by the way… So, I tried to derive the Friedmann equation by applying the gravitational self-energy model. 2nd Friedmann equation, The 2nd Friedman eq. is fine, but the 1st Friedman eq. seems to have a problem. Which one is right? Please advise. 1. A form in which negative mass is placed in the mass density term There are some problems with this equation. If the negative mass term is greater than the positive mass term, the right-hand side can be negative. 2. The cosmological constant is the first Friedman eq. and the second Friedman are the same in eq., so put the same terms in. 3. If the negative mass is greater than the positive mass, there is a curvature reversal, Accordingly, is there a sign inversion? Any advice would be appreciated.

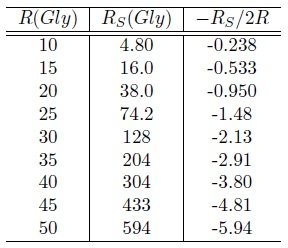
[ key summary ] 1. Gravitational potential energy is negative energy In Wikipedia, refer to the gravitational binding energy entry, Two bodies, placed at the distance R from each other and reciprocally not moving, exert a gravitational force on a third body slightly smaller when R is small. This can be seen as a negative mass component of the system, equal, for uniformly spherical solutions, to: -M_binding = -(3/5)GM2/Rc2 In the dimensional analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of (mass) x (speed)2. So, E=Mc2 holds true for all kinds of energy. "-Mgs" is the equivalent mass of gravitational self-energy. It is a negative equivalent mass term. The greater the mass, the greater the gravitational self-energy ratio. Earth's -Mgs = (- 4.17x10-10)M_Earth Sun's -Mgs = (- 1.27x10-4)M_Sun Black hole's -Mgs = (- 0.3)M_black-hole 2. In the universe, if we calculate the gravitational self-energy Since the particle horizon is the range of interaction, if we find the mass energy (Mc2) and gravitational self-energy ((-Mgs)c2) values at each particle horizon, Mass energy is an attractive component, and the equivalent mass of gravitational self-energy is a repulsive component. Critical density value p_c = 8.50 x 10^-27[kgm^-3] was used. At particle horizon R=16.7Gly, (-Mgs)c2 = (-0.39M)c2 : decelerated expansion period At particle horizon R=26.2Gly, (-Mgs)c2 = (-1.00M)c2 : inflection point (About 5-7 billion years ago, consistent with standard cosmology.) At particle horizon R=46.5Gly, (-Mgs)c2 = (-3.04M)c2 : accelerated expansion period Even in the universe, gravitational potential energy must be considered. And, in fact, if we calculate the value, since gravitational self-energy is larger than mass energy, so the universe has accelerated expansion. Gravitational self-energy accounts for decelerated expansion, inflection point, and accelerated expansion.

A-2. Your thoughts and arguments remind me of the following question. In a black hole, is it impossible to compress within r<R_gs? In the universe, cannot the state r<R_gs exist? a) Existing Model. b) New Model. The area of within R_{gs} has gravitational self-energy(potential energy) of negative value, which is larger than mass energy of positive value. If r is less than R_gs, this area becomes negative energy (mass) state. There is a repulsive gravitational effect between the negative masses, which causes it to expand again. This area (within R_gs ) exercises anti-gravity on all particles entering this area, and accordingly prevents all masses from gathering to r=0. Therefore the distribution of mass (energy) can't be reduced to at least radius R_gs (or R_{gs - vir}). By locking horns between gravitational self-energy and mass energy, particles inside black hole or distribution of energy can be stabilized. As a final state, the black hole does not have a singularity in the center, but it has a Zero (total) Energy Zone (ZEZ). R_gs is the maximum of ZEZ. By the way, I can imagine the state where r<R_gs and I think it is possible. I'm thinking of a negative mass state, and I'm not at all against it. In the universe, the event horizon for a black hole formed by a mass distribution of R=46.5 Gly is approximately 491.6 Gly. In the universe, the R_gs formed by a mass distribution of R=46.5 Gly is approximately 147.5 Gly. So, the observable universe 46.5Gly already exists within R_gs. It is said that the negative gravitational self-energy is greater than the positive mass energy. Consider the Schwarzschild solution. The singularity problem does not apply to general relativity, nor does physics itself apply. Is this expression complete? If this solution was complete ==> there should be no singularity problem. In other words, there is something we're missing out on. Repulsion is required to solve the singularity problem. It doesn't necessarily have to come from quantum mechanics. It's just that we thought the solution to that would be in quantum mechanics. Since it is being compressed by gravity, wouldn't it be okay to come out of the same type of force, anti-gravity? We also have the dark matter dark energy problem. And, to solve this problem, We also accepted the bizarre assumption that the energy density is constant as it expands, and also notion the that has a positive energy density and exerts a negative pressure. The magnitude of the pressure is also strange. Even for the fastest light, it is (1/3)p, which is three times larger than this. Since pressure is related to kinetic energy, to have a value three times greater than that of light~. it's still weird. Despite introducing such a bizarre existence, it has an error of 10^120, and also has a Fine tuning problem and a CCC problem. A lot of people hang around at the beginning of my argument. Does negative energy exist? Is gravitational potential energy negative energy? Don't think about whether negative energy exists or not. Don't even think about "Is gravitational potential energy negative?" If you, reading this article, find it difficult to accept it, think that it is just an assumption and move on to the next process. Can the phenomenon be explained by introducing assumptions? Can the deceleration expansion period, the inflection point, and the accelerated expansion period be explained? Are these periods consistent with current observations, or are they likely to be explained? Just do the math first. If you succeed in explaining the phenomenon, there is another way to come back and look at the notion of negative energy. We are already imagining and trying something more bizarre than gravitational potential energy. I hope you try the calculation with gravitational potential energy as well. This is a concept that already exists and has been proven. And gravitational self-energy has the potential to explain the singularity problem and dark energy.

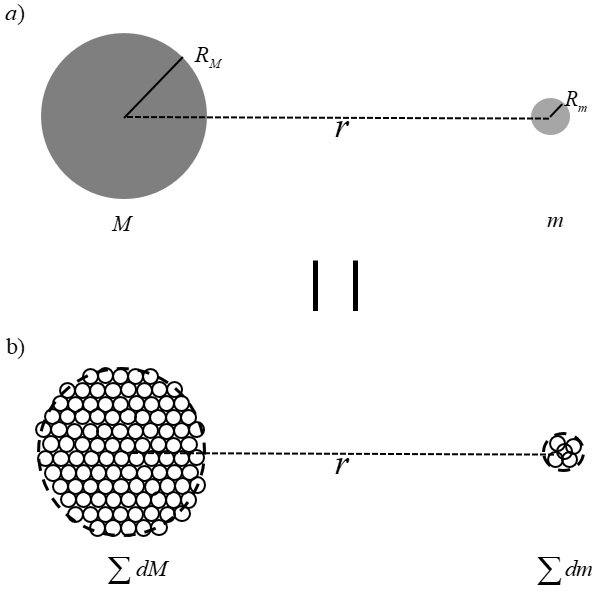
First of all, I apologize for my lack of knowledge and lack of English. I know only the name of the Landau-Lifschitz pseudotensor, not the specifics. Nevertheless, speaking out, I ask for your understanding. I also know that the problem is difficult to solve because the energy of the gravitational field cannot be localized. So, I came up with a slightly different approach. I can do it at my level. This is from Chapter 1-2 of my thesis.(1-11P) A-1. The necessity and possibility of gravitational self-energy In the Schwarzschild solution. The only important variables are the mass M and the distance r. So, only the mass M is important. Then, to find the solution of the strong gravitational field, we only need to find the equivalent mass of the gravitational field. 2-2. Equivalent mass of gravitational potential energy Now, all we need to do is list all the gravitational potential energies and find their equivalent mass. U_T = ΣU_i = Σ-M_{gp,i} - M_{gp,i} is the equivalent mass of gravitational potential energy. Most of the situations we need to analyze are two-body problems. The principle of the multi-body problem is similar. There is a mass M and mass m. Mass M and m are made up of several particles. If we find the gravitational potential energy of all particles, it looks like there are many terms, but if we organize it, we can organize it into three terms. The gravitational self-energy of the mass M + the gravitational self-energy of the mass m + the gravitational potential energy of the mass M and mass m. The gravitational problem we face is to establish and solve the equation of motion when mass M and mass m are separated by a distance r. U_{gs - M}: Total gravitational potential energy of large mass M = gravitational self-energy of large mass M U_{gs - m}: Total gravitational potential energy of small mass m = gravitational self-energy of small mass m U_{gp - Mm}: The gravitational potential energy between the large mass M and the small mass m Although the system contains countless particles, it can be summarized in three terms. The U_{gp - Mm} term is difficult to localize, but U_{gs - M} and U_{gs - m} are easy to localize. Also, the equivalent mass of U_gs-M has the same center of mass as the mass M. The equivalent mass of U_gs-m has the same center of mass as mass m. What is necessary is just to find the equivalent mass corresponding to this gravitational potential energy. This value only differs depending on the specific situation. In individual situations, if the internal structure of the mass M and the mass m is presented, it is possible to obtain an accurate value. For example, suppose that the mass is uniformly distributed in a spherical shape as shown in the figure above. Now, let's compare how much each size has compared to the mass energy Mc^2(main source of gravity). Knowing the size of each, we can decide whether we should consider or ignore the corresponding physical quantity. 2-2-1. The gravitational self-energy of the gravitational source M The magnitude of gravitational self-energy at the Schwarzschild radius It can be seen that the gravitational self-energy effect is quite large. At the Schwarzschild radius of an object, it can be seen that the magnitude of negative gravitational self-energy is 30% of the free state. Since the gravitational self-energy is negative, the mass M does not fully work in a black hole, but acts as much as the gravitational potential energy is subtracted, and as a result, it becomes the same as the state with a mass of 0.7M. As experienced in elementary particle physics, we can think of mass defect due to binding energy. The bound state is a state in which the total mass is reduced by the difference in binding energy compared to the free state. The good thing about gravitational self-energy is that the principle that assumes that all mass is gathered at the center of mass can be used for the equivalent mass formed by gravitational self-energy. The small mass m may be treated as a test mass, and the small mass m itself may be considered as the total mass reflecting its gravitational energy. So, the small mass m is not important. so pass. 2-2-3. Gravitational potential energy between mass M and mass m In the case of M>>m or r>>R_S, the U_{gs - Mm} term is negligible. When considering the motion of particles near a black hole, it can be seen that this value is very small compared to the mass energy Mc^2 of the gravitational source and can be ignored. However, in cases such as collisions of black holes of similar mass, this term should be taken into account. This term has a maximum value when R=R_{S}, and since r is in the denominator, if it is considerably farther than the distance of R_{S}, it is also small compared to the gravitational self-energy of the gravitational source M. In summary, in the situation where M>>m or r>>R_S, only the first term, the gravitational self-energy of the gravitational source M, needs to be considered. 2-2-5. When the test particle is near a source of gravity with a strong gravitational field Since the second and third terms can be ignored, the equivalent mass of the gravitational potential energy is simplified. The above suggests that the gravitational self-energy term of the gravitational source should be considered. In particular, the fact that the center of the equivalent mass of the gravitational potential energy coincides with the center of mass of the gravitational source makes the situation convenient. 2-3. Under the general theory of relativity, a solution in a strong gravitational field In all existing solutions, the mass term M must be replaced by (M) + (- M_gs) And, this has very significant consequences. It solves the singularity problem that the existing solution had. This equation means that if mass M is uniformly distributed within the radius R_gs=0.3R_S, gravitational self-energy for such an object equals mass energy in size. So, in case of such an object, mass energy and gravitational self-energy can be completely offset while total energy is zero. Since total energy of such an object is 0, gravity exercised on another object outside is also 0. This means that there exists the point where negative gravitational self-energy becomes equal to mass energy within the radius of black hole, and that, supposing a uniform distribution, the value exists at the point 0.3R_S, a 30% level of the black hole radius. Even with kinetic energy and virial theorem applied only the radius diminishes as negative energy counterbalances positive energy, but no effects at all on this point: "There is a zone which cannot be compressed anymore due to the negative gravitational potential energy." Although potential energy changes to kinetic energy, in order to achieve a stable bonded state, a part of the kinetic energy must be released to the outside of the system. Considering the virial theorem (K=-U/2)), R_{gs-vir} = (1/2)R_gs = 0.15R_S Since this value is on a level not negligible against the size of black hole, we should never fail to consider "gravitational self-energy" for case of black hole. In case of the smallest black hole with three times the solar mass, R_S = 9km. R_gs of this black hole is as far as 3km. In other words, even in a black hole with smallest size that is made by the contraction of a star, the mass distribution can't be reduced to at least radius 3km(R_{gs - vir} = 1.5km). From the equation above, even if some particle comes into the radius of black hole, it is not a fact that it contracts itself infinitely to the point R = 0. From the point R_{gs} (or R_{gs - vir}), gravity is 0, and when it enters into the area of R_{gs} (or R_{gs - vir}), total energy within R_{gs} (or R_{gs - vir}) region corresponds to negative values enabling anti-gravity to exist. This R_{gs} (or R_{gs - vir}) region comes to exert repulsive gravity effects on the particles outside of it, therefore it interrupting the formation of singularity at the near the area R=0. If you(It means the unspecified majority of people reading this article.) have only the concept of positive energy, please refer to the following explanation. From the point of view of mass defect, r=R_{gs} (or R_{gs - vir}) is the point where the total energy of the system is zero. For the system to compress more than this point, there must be an positive energy release from the system. However, since the total energy of the system is zero, there is no positive energy that the system can release. Therefore, the system cannot be more compressed than r=R_{gs} (or R_{gs - vir}). So black hole doesn't have singularity. The gravitational self-energy can solve the singularity problem, and it has the potential to solve the dark energy problem as well. 1)https://www.researchgate.net/publication/359329109 2)https://www.researchgate.net/publication/313314666_Solution_of_the_Singularity_Problem_of_Black_Hole

First of all, I apologize for my lack of knowledge and lack of English. Hans ohanian's claim. The content of the book. 1) He argues many times that gravitational self-energy is the source of gravity, and that gravity should be exerted. 2) The meaning of the sentence he wrote means that the equivalence of inertial mass and gravitational mass must be established even for gravitational self-energy. The sentence before the sentence above 3) Now the remaining question is, is gravitational self-energy or gravitational potential energy positive energy? Is it negative energy? So, does it have positive (inertial) gravitational mass? Does it have negative (inertial) gravitational mass? In Wikipedia, Gravitational binding energy https://en.wikipedia.org/wiki/Gravitational_binding_energy If the gravitational potential energy is positive energy, the mass increase phenomenon only occurs. So, a reasonable way to explain the situation is to Gravitational potential energy and gravitational self-energy are negative energy, and have negative inertial mass and negative gravitational mass. If you feel repulsed by the word "have", Gravitational potential energy and gravitational self-energy are negative energies, corresponds to negative inertial mass and negative gravitational mass. Then, we can give a reasonable explanation for the gravitational action on the distant m_3, as in the above equation.

Some literature on gravitational self-energy 1. Gravitation and Spacetime (Book) : 25~29P https://www.amazon.com/Gravitation-Spacetime-Second-Hans-Ohanian/dp/0393965015 Table 1.3 also includes a result for gravitational energy, which was obtained by different means. The E¨otv¨os experiments do not permit a direct test of the hypothesis that gravitational energy contributes to the gravitational mass, because the ostensible macroscopic amounts of gravitational self-energy in masses of laboratory size are much too small to affect these experiments. Theoretical considerations suggest that the rest masses of electrons, protons, and neutrons include large amounts of gravitational self-energy, but we do not know how to calculate these self-energies (for the implications of this, see the later discussion). If we want to discover whether gravity gravitates, we must examine the behavior of large masses, of planetary size, with significant and calculable amounts of gravitational self-energy. Treating the Earth as a continuous, classical mass distribution (with no gravitational self-energy in the elementary, subatomic particles), we find that its gravitational self-energy is about 4.6 × 10?10 times its rest-mass energy. The gravitational self-energy of the Moon is smaller, only about 0.2 × 10?10 times its rest-mass energy. If gravitational self-energy does not contribute in the normal way to the gravitational mass, then the Earth and the Moon would fall at different rates in the gravitational field of the Sun. The difference in the rates of fall is effectively equivalent to a uniform extra force field pulling the Moon toward the Sun (if gravitational energy gravitates less than normal) or away from the Sun (if gravitational energy gravitates more than normal). Such an extra force leads to a distortion of the orbit of the Moon relative to the Earth, a distortion called the Nordvedt effect. As Fig. 1.12 shows, the orbit is elongated, or polarized, in the direction of the Sun. Although the distortion effect is small, very precise measurements of the Earth-Moon distance have been performed by the laserranging technique already mentioned in Section 1.2, with a pulse of laser light sent from the Earth to the Moon and reflected back to the Earth by the corner reflectors installed on the Moon during the Apollo mission. Measurements of the travel time of the pulse determine the distance to within an uncertainty of a centimeter, and recent improvements are reducing this to a millimeter. If the uncertainty is taken as 1 cm, the analysis of the orbital data places a direct limit of 5 × 10?4 on the fractional difference between the contributions of gravitational energy to the inertial and the gravitational mass. Thus, these experiments indicate that gravitational energy gravitates in the normal way. The observed equality of gravitation and inertia for all forms of energy means that any system, containing any combination of the different kinds of energy, will have equal gravitational and inertial masses. Thus, we will now adopt Newton’s principle of equivalence, m_G = m_I , as an exact relation that our gravitational theory must satisfy. 2. Explanation of GRAVITY PROBE B https://einstein.stanford.edu/conten...ty/a11278.html Do gravitational fields produce their own gravity? Yes. A gravitational field contains energy just like electromagnetic fields do. This energy also produces its own gravity, and this means that unlike all other fields, gravity can interact with itself and is not 'neutral'. The energy locked up in the gravitational field of the earth is about equal to the mass of Mount Everest, so that for most applications, you do not have to worry about this 'self-interaction' of gravity when you calculate how other bodies move in the earth's gravitational field. 3. Wikipedia, Gravitational binding energy https://en.wikipedia.org/wiki/Gravitational_binding_energy *A few years ago, when I claimed that content, there was no "negative mass component" item in the Wiki's gravitational binding energy item, but someone added an explanation. Two bodies, placed at the distance R from each other and reciprocally not moving, exert a gravitational force on a third body slightly smaller when R is small. This can be seen as a negative mass component of the system, equal, for uniformly spherical solutions, to : Since the universe also has gravitational potential energy between all materials and is in a binding state, For the universe, the mass defect effect due to gravitational self-energy or the negative equivalent mass effect must be considered. And, in fact, if we calculate the value, since gravitational self-energy is larger than mass energy, the universe has accelerated expansion. Moreover, the gravitational self-energy is smaller than the mass energy when the particle horizon is small, and it can be found that the effect becomes larger as the particle horizon becomes larger. Since the gravitational self-energy model suggests decelerating expansion, inflection point, and accelerated expansion, serious research from someone better than me is needed. Since gravitational potential energy or gravitational self-energy is a concept that already exists, it is generating the effect of dark energy~ There will already be calculation results for the density function in someone's paper. Find it and try to calculate Mc2 and Ugs.

You borrow money, but is the situation in which you owe money the same as the situation in which you do not owe money? Mass defect due to binding energy Consider situations a) and c) In a), the total mass of the two particle systems is 2m, and the total energy is ET=2mc2 In c), is the total energy of the two-particle system ET=2mc2 ? In c), when the two particle systems act gravitationally on an external particle, will they act gravitationally with a gravitational mass of " 2m "? Are a) and c) the same mass or same state? If you do not apply negative binding energy, the conclusions you get will not match the actual results. In c), the total energy of the two particle systems is In the dimension analysis of energy, E has kg(m/s)2, so all energy can be expressed in the form of mass x (speed)^2. So, E=mc2 (Here, m is not used as a word for rest mass, but for mass.) holds true for all kinds of energy. If we introduce the equivalent mass -mgp for the gravitational potential energy, The gravitational force acting on a relatively distant third mass m3 is That is, when considering the gravitational action of a bound system, not only the mass in its free state but also the binding energy term should be considered. Alternatively, the gravitational force acting on the bound system can be decomposed into a free-state mass term and an equivalent mass term of binding energy. While we usually use the mass m* of the bound system, we forget that m* is (m - mbinding_energy). Gravitational potential energy is also a kind of binding energy. A proton or a hydrogen atom itself is already a binding system, and we are using m*. In the universe, the current situation is So, the universe is accelerating expansion.

2-4-3. The ratio of increase in gravitational self-energy to increase in mass energy If the particle horizon increases and a positive mass is produced by " M ", the equivalent mass of negative gravitational potential energy is produced by " - 5.14 M ". This value is not a fixed value, it depends on the density and the size of the particle horizon. The density used the current critical density, but the density is a variable. Please see the approximate trend. As R increases, The rate of increase of gravitational self-energy tends to be greater than the rate of increase of mass energy.

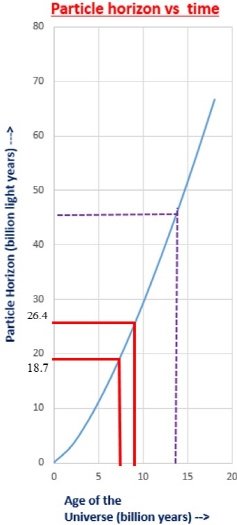
The source of dark energy is gravitational self-energy. 1. The need for negative energy density 1) Negative energy (mass) density in standard cosmology From the second Friedmann equation or acceleration equation, In standard cosmology, it is explained by introducing an entity that has a positive mass density but exerts a negative pressure. ρΛ + 3PΛ = ρΛ+3(-ρΛ) =- 2ρΛ However, If we rearrange the dark energy term, the final result is a negative mass density of - 2ρΛ . There are too many people who have an aversion to negative energy (mass). However, in the standard cosmology, accelerated expansion is impossible without negative mass density. It is just that the negative mass density term is called negative pressure, so it is not recognized. 2) The energy of a gravitational field is negative In his lecture, Alan Guth said: Stephen Hawking also argued that zero energy state could be maintained when mass energy and gravitational potential energy were offset each other at the inflation period only. 3) Earth's and Moon's Gravitational self-energy 4) Our common sense was wrong long ago Our conventional wisdom is already wrong about the accelerated expansion of the universe and the rotation curve of galaxies. So, instead of thinking about whether negative energy exists, we should focus on whether the universe is explained by the introduced physical quantity. For those of you who are still reluctant to negative energy, first assume that gravitational potential energy is negative energy, and then look at the following logic. 2. Comparison of magnitudes of mass energy and gravitational self-energy in the observable universe 1)Total mass energy (include radiation energy) of the observable universe (particle horizon) Simply put, the particle horizon is important because it means the range of the interaction. The critical density value p_c = 8.50 x 10-27[kgm-3 ] was used. Observable universe (particle horizon) radius : 46.5Gly. Since the universe is almost flat spacetime, the total mass energy in the particle horizon is The repulsive force component is approximately 3.04 times the attractive force component. The universe is accelerating expansion. For reference, assuming the current average density, in the cosmic horizon 16.7Gly, U/Mc2 = -0.39 is obtained. At the cosmic horizon 16.7Gly,the repulsive force component is smaller than the attractive force component, suggesting that it is a period of decelerated expansion. 3. Find the inflection point where the attractive and repulsive components are equal I searched for the point at which the universe transitions from decelerated expansion to accelerated expansion. I do not know the magnitude Rgs at which the positive mass energy and the negative gravitational potential energy are equal, since I do not have the data of the density. We only need to understand the general flow and possibility, so let's get ? by putting in the current critical density value. Rgs = 26.2Gly Assuming that the average density is approximately 1.25 times the current average density, we get Rgs = 23.7Gly. Assuming that the average density is approximately 2 times the current average density, we get Rgs = 18.7Gly. Comparing the data from the existing particle horizon graph, it is estimated that it is approximately 5 to 7 billion years ago from the present. It is necessary to review this model because it includes the transition of the universe to the period of decelerated expansion, the inflection point, and the period of accelerated expansion. Particle horizon vs time. We need to know the average density to get an accurate value. However, as a rough estimate, according to this model, it is estimated that the transition to accelerated expansion was approximately 5-7 billion years ago. 4. The ratio of increase in gravitational self-energy to increase in mass energy If the particle horizon increases and a positive mass is produced by M, the equivalent mass of negative gravitational potential energy is produced by -5.14 M. This value is not a fixed value, it depends on the density and the size of the particle horizon. 5. Increase in dark energy (gravitational self-energy) due to increase in particle horizon 1)Particles and galaxies spread almost uniformly throughout the universe through the inflation process. 2)Galaxies move according to the Hubble-Lemaitre law. 3)On the other hand, the propagation speed of the field, the range of interaction (particle horizon), has the fastest speed, the speed of light in expanding space. 4)Thus, over time, many new substances (matters and galaxies) enter the particle horizon. In other words, the newly entering materials undergo gravitational interaction, resulting in an increase in mass energy and an increase in gravitational potential energy in the region within the particle horizon. 5)By the way, while mass energy is proportional to M, total gravitational potential energy (gravitational self-energy) is proportional to - M2/R. As M increases, the gravitational potential energy increases faster. Accordingly, the repulsive force component increases faster than the attractive force component. 6)The increase in gravitational potential energy due to the newly incorporated matter into the particle horizon is causing the dark energy. The same principle is applicable to the birth of energy within a particle horizon. That is, when the mass energy increases by M, the gravitational self-energy increases by - M2/R. 7)In the present universe, it is predicted that the dark energy effect (repulsive effect) surpassed the gravitational effect of matter and dark matter about 5 billion years ago. According to this model, it is the point at which the positive mass energy and the negative gravitational self-energy are equal. Knowing the average density function, we can get the exact value. 8)Gravitational potential energy is a concept that already exists and is negative energy that can create repulsive force. This model produces similar results to the phenomenon of applying negative pressure while having positive (inertial) mass density. As the particle horizon expands, the positive mass increases(New influx or birth of matter), but the negative gravitational potential energy created by these positive masses is greater. While having a positive inertial mass, it is creating a negative gravitational mass that is larger than the positive inertial mass. Because of this factor, this model should be reviewed. 6. How to validate the dark energy model that gravitational self-energy is the source of dark energy 1)Find the expressions of p(t) and Rph(t) p(t) is the average density inside the particle horizon. Rph(t) is the particle horizon. 2)At each time, within the particle horizon Find E = M(t)c2 and Ugs = - (3/5)(GM(t)2/R E = M(t)c2 is the attractive energy component and Ugs is the repulsive energy component. 3)Compare Ugs/E with the observations Anyone familiar with particle horizons and density functions can verify this model. *The potential of this model 1. Description of the current accelerated expansion R = 46.5Gly, the ratio of the attractive component to the repulsive force component, U/Mc2= - 3.04, and the negative energy component and the repulsive force component are larger, explaining the accelerated expansion. 2. Numerically, it represents the change from decelerated expansion to accelerated expansion, and by calculating the inflection point, it can be compared with the observed value. The roughly calculated inflection point is 5 to 7 billion years ago, So this model has potential. 3. In standard cosmology, dark energy is an object that has a positive energy density and exerts a negative pressure. The gravitational self-energy provides an explanation for this bizarre property. 1) Characteristics: It has a positive mass (energy) density and acts as a negative gravitational mass. 2) Size: Produces a negative gravitational mass density that is greater than the positive inertial mass density. The repulsive component is greater than the attractive component. The gravitational self-energy accounts for both of these properties. Mass energy is positive energy and is attractive, whereas gravitational self-energy is negative energy and has repulsive properties. Mass energy is proportional to M. On the other hand, gravitational self-energy is proportional to -M2/R. At a size smaller than Rgs (The magnitude at which the positive mass energy and the negative gravitational self-energy are equal.), the mass energy is greater than the gravitational self-energy created by positive masses, and at a size larger than Rgs , the gravitational self-energy created by positive masses is greater than the mass energy. 4. Since gravitational self-energy is pointed out as the source of dark energy, verification is possible. #On the solution of the strong gravitational field the solution of the Singularity problem the origin of Dark energy and Dark matter https://www.researchgate.net/publication/359329109

Please delete this post $\frac{1}{3}$ [tex]\frac{1}{3} [/tex] [tex]\frac{1}{R}(\frac{{{d^2}R}}{{d{t^2}}}) = - (\frac{{4\pi G}}{3})(\rho + 3P)[/tex]

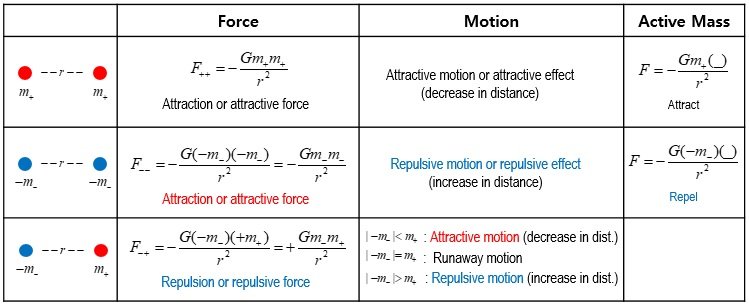
Observations do not prove that the negative mass does not exist in the universe. You must have heard this problem in science philosophy many times~ And isn't my explanation in the text? This is not clear evidence, but there are likely observations, so further research is needed. And, in 2018, a researcher named Farnes published the following paper at Astronomy and Astrophysics (A&A). He seems to claim that observations of several galaxies are evidence. https://phys.org/news/2018-12-bizarre-dark-fluid-negative-mass.html *A Unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework (2018, J.S. Farnes) https://arxiv.org/abs/1712.07962 (*In fact, In 2009 I wrote a paper describing both dark matter and dark energy using negative mass. The first post on the forum here also raised this claim.)

I have said many times that I have never made such a claim. Please stop the matter. ===== No. Both electron and positron have positive mass. ===== 1) Pair creation of two positive mass particles : In the process of the pair creation of electron and positron, ~~~ 2) Pair creation when one has positive mass and the other has negative mass ===== I have never claimed that antimatter is a negative mass. =====

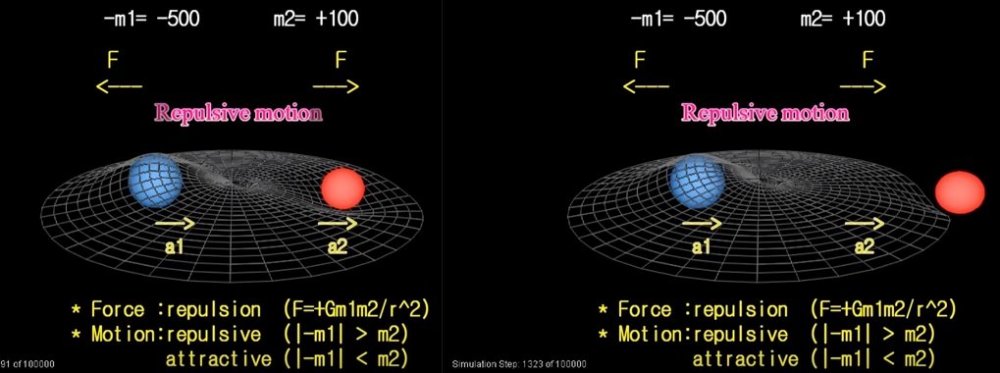
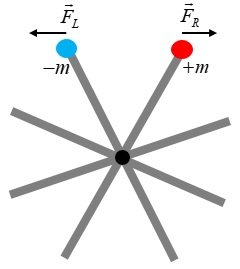
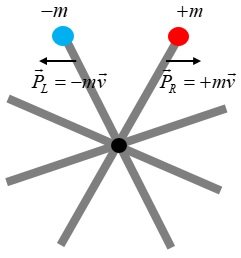
Acceleration is determined by the size of the opponent's mass. If the absolute value of the negative mass is greater than the absolute value of the positive mass, there is a repulsive gravitational effect between the two. In this case, the acceleration of positive mass is greater. As time passes, the two masses become more and more distant. Thus, they can exist without pair annihilation. In case |-m_ -| > m_ + We need a mechanism to return something to its original vacuum state after something is born in the vacuum, and we need a mechanism to exist after something is born from the vacuum. The mechanism of different mass sizes during pair creation seems to play a very important role. [Big bang mechanism or creation mechanism(tentative name) ] This logic may be used as a theoretical basis(energy conservation law, mass difference(repulsive gravitational effect)) for the presence of two masses after pair creation without pair annihilation.

Yes! I know too. I have never claimed that antimatter is a negative mass. I don't know why you keep saying that. What I'm explaining for example is this phrase above. One of the backgrounds that the public makes this assumption(conjecture) is the experience gained during pair creation of electron and positron. It(pair creation of electron and positron) is only intended to explain that experience differs from the situation at pair creation of negative and positive masses.

In simple terms, 1) Pair creation of two positive mass particles : In the process of the pair creation of electron and positron, electron's mass(energy) = positron's mass(energy) = +10, potential energy = +1 or -1 +10 : +10 ////// +10 : +10 -1 : -1 ////// +1 : +1 -------------- ////// -------------------- +9 = +9 ////// +11 = +11 2) Pair creation when one has positive mass and the other has negative mass But, in the process of the pair creation of negative and positive mass, negative mass(energy) = -10, positive mass(energy) = +10, -10 : +10 ////////// -10 : +10 -1 : -1 ////////// +1 : +1 ---------------- ////// -------------------- |-11| ≠ | +9| ////// | -9| ≠ |+11| With the sign of negative mass and positive mass different, the difference occurs because the potential energy has a sign of either + or - .

No. Both electron and positron have positive mass.

[ False claims about negative mass : Runaway motion problem, Vacuum instability problem, Wheel problem ] 1. The runaway motion problem is wrong. Runaway motion is an argument that the two masses continue to accelerate, in an ideal situation where the negative mass and the positive mass are exactly the same. Runaway motion is used as a rejection logic of negative mass. a) The difference in mass when creating the pair of negative mass and positive mass. As a general conjecture, when positive and negative mass are born, the mass will be exactly the same, but this conjecture is wrong. There is at least a gravitational potential energy (binding energy) between the two particles. Process of the pair creation of electron and positron, the effect of electromagnetic potential energy could be the same because the two particles had the same kind of energy(electron : +, positron : +). Therefore, the two particles could have the same mass. However, in the process of the pair creation of negative and positive mass, the effect of gravitational potential energy is different because the two particles have different types of energy(negative mass : - , positive mass : +). This gravitational potential energy has a positive value and exists in a system containing two objects or two objects. If you add or subtract potential energy in two cases(Pair creation of electron and positron, Pair creation of negative mass and positive mass), you can see that they are different. In case the negative mass and the positive mass are pair created in the vacuum, according to the Energy Conservation Law, there must be a mass difference between the negative mass and the positive mass. |-m_ -| > m_ + Acceleration is determined by the size of the opponent's mass. If the absolute value of the negative mass is greater than the absolute value of the positive mass, there is a repulsive gravitational effect between the two. In this case, the acceleration of positive mass is greater. As time passes, the two masses become more and more distant. In other words, the ideal situation of pairing is broken. Because the accelerations are not the same and the distance of the pairing increases, the interaction of the other particles becomes involved. Therefore, runaway motion is not maintained. b) There is a possibility that the gravitational potential energy will break the ideal situation. Although the absolute values of the masses of two objects are exactly the same, there is a gravitational potential energy between them. Thus, these experiments indicate that gravitational energy gravitates in the normal way. - Gravitation and Spacetime – by Hans C. Ohanian and Remo Ruffini That is, even if the masses of negative mass and positive mass are exactly the same, the gravitational potential energy between them breaks this ideal situation. c) Since "runaway motion'' assumes a very ideal situation, an unusual movement occurs, but in the real world, this ideal situation may be broken by external factors (forces or fields by other objects …) d) ~~~ 2. The vacuum instability problem is wrong. In case of a positive mass, it could have negative energy level within negative potential. Nevertheless, even in this case, the total energy containing potential energy was still in the state of positive energy. However, for positive mass to enter the domain of (total energy is negative) negative energy level, energy should have negative value, and this means that it should have the characteristics of negative mass. When negative mass exists within potential with maximal and minimal points, different directions of force and acceleration should be considered for negative mass. F=-ma (m>0) a=-F/m The acceleration of negative mass is opposite to the direction of force. Therefore, the negative mass has harmonic oscillation at the maximum point and it is also stable at the maximum point. In the case of positive mass, it was stable at the minimum point at which energy is the low. However, in case of negative mass, stable equilibrium is a point of maximum value, not a point of minimum value. It is stable at a low energy state in the case of positive mass. However, it is stable at a high energy state in the case of negative mass. Due to this, “the problem of transition to minus infinite energy level'' does not occur, therefore negative mass(energy) and positive mass(energy) can exist stably in our universe. ~~~ 3. The wheel problem is wrong. What happens if one attaches a negative and positive mass pair to the rim of a wheel? This is incompatible with general relativity, for the device gets more massive. -Thomas Gold, in Negative mass in general relativity. a) In terms of force There is a problem of "How do you combine a negative mass with a rod?" But let's assume that it is connected in any way. The forces acting on both rods are equal in magnitude and opposite directions. F_{L} = - F_{R} Therefore, the wheel does not rotate. b) In terms of momentum In order for the wheel to move, momentum must be transmitted to the rod. But, P_{L} = - P_{R} The momentum transmitted to both rods is completely canceled. Therefore, the wheel does not rotate. He should have thought that the momentum had to be transmitted in order for the wheel to rotate. Fig.x. Different forms of explanation based on criteria(Force, Motion, Active Mass). Due to the negative inertial mass, the direction of force and motion changes [ Resurrection Request for Negative Mass. ] All new discoveries were called new discoveries because they were not found until then. Throughout the history of science, among the things that have not yet been discovered, new discoveries have had many examples. In other words, it does not guarantee that undiscovered findings of any physical object will be undiscovered in the future. The history of physics, and even the history of science. And even if we find something, our existing knowledge either rejects this discovery or tries to interpret it through existing ideas. ======= Negative Mass? Actually the first indication of the discovery! Days later… What does this mean? There cannot be negative mass, but would Einstein’s Cosmological Constant explain this acceleration? ======= In 1998 observations, the first result of the Friedmann equation was negative (gravitational) mass density. But the researchers, who had difficulty accepting negative masses, modified the equation. And they argue that the accelerated expansion of the universe is evidence of the existence of a cosmological constant. From the second Friedmann equation or acceleration equation, Since ρ is energy density in the acceleration equation, the pressure term P also has a dimension of energy density(c=1). Current acceleration equation inevitably require negative (gravitational) mass density. The mainstream produces acceleration expansion by setting the pressure of the cosmological constant or vacuum energy to P = -ρ However, the notion(dark energy term) created by the mainstream has an inertial mass density of +1(p), equivalent mass density of kinetic energy(or pressure term) of -3(p), with gravitational mass density of -2(p). Not only different signs, but different values. It violates? the principle of equivalence of inertial mass and gravitational mass, which is the basis of general relativity theory. Looking at the dark energy term, - 2ρ = ρ + 3( -ρ ) = - 2ρ ~~~~ In the process of discarding the negative mass that is the result of the field equation, it is assumed that the false claims listed above played a key role. Since the rejection logics for the negative mass are wrong, the negative mass model needs to be reviewed again. *Regardless of the problem of dark matter and dark energy, the above three arguments are the core problem of negative mass. ======== # Paper 1) https://www.researchgate.net/publication/286935998 2) https://www.researchgate.net/publication/324525352