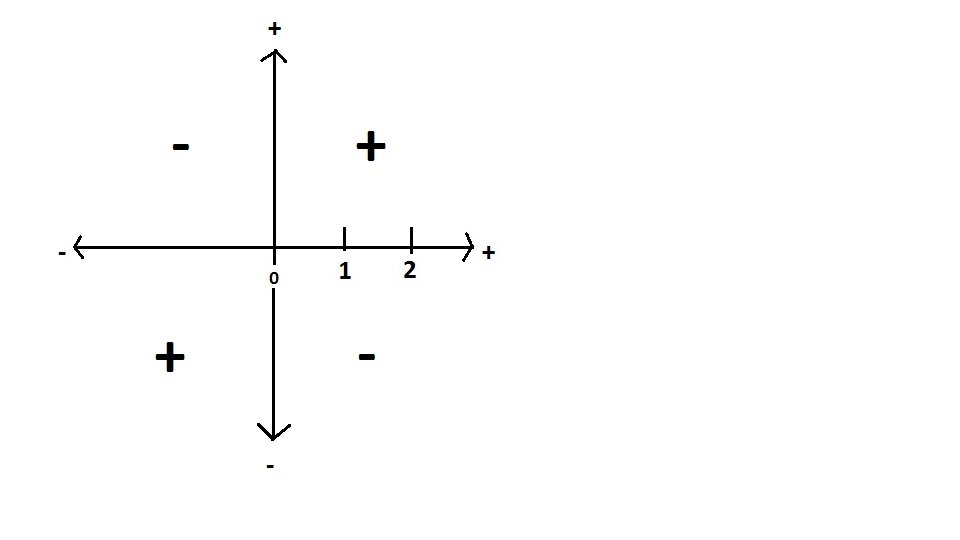michel123456

It is negative. And I guess all these points are upon an hyperbola. But I don't know if that can have a deeper signification. That was not my goal.

This one, both axes If they are labelled i on both axes we have Point A has coordinates 6i, 9i The area of the green rectangle is 6i.9i=54i^2=-54 It has area the number -54, that you can also put on the number line at position -54.

Could you please label your axis? I don't follow.

I guess it represents the number -54. As if the area were representing a distance upon the number line.

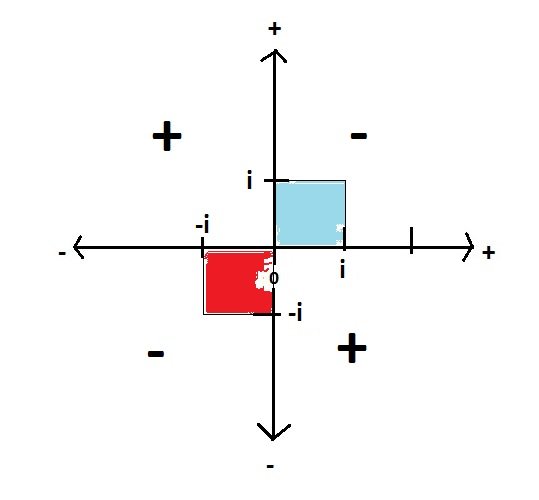
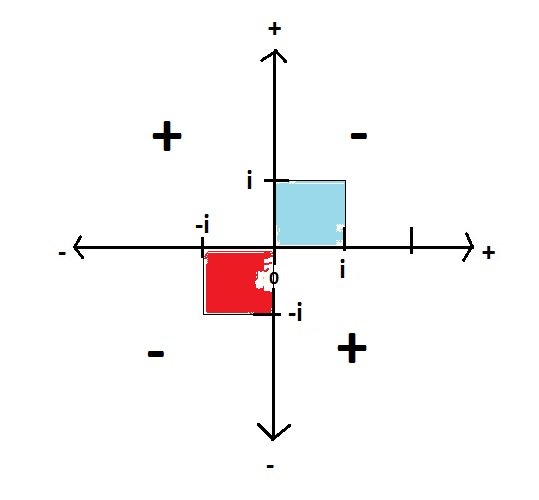
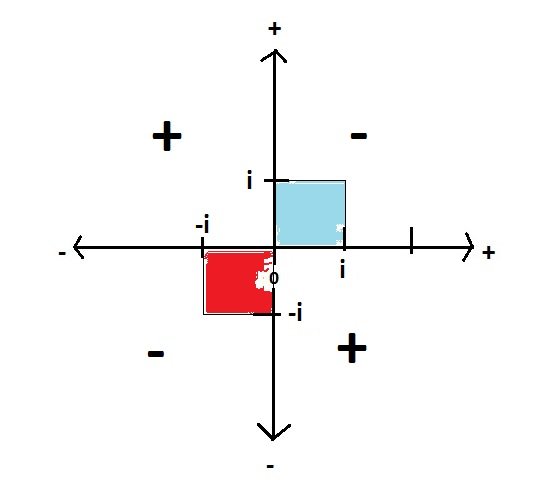
I understand that the surface of my "i diagram" is spread with real numbers. That the blue square is a "real square" of imaginary side. And so is the red square. And that those squares are not representing areas but maybe a weird unauthorized representation. All of which make the imaginary numbers totally different from the real numbers. Which again makes me wonder how can you consider correct to create a representation with an axis of imaginary numbers orthogonal to an axis of real numbers just as if they were of equivalent nature. https://en.wikipedia.org/wiki/Imaginary_number#/media/File:Complex_conjugate_picture.svg In this diagram, how do we infer that iy has a positive value? How do we treat the imaginary line on the same ground with the real number line? Where are the positive & negative? I mean, one would automatically infer that the positive numbers are on the upper right sector. Is it so? And why?

I'll try to explain. I have those 2 graphs: If I try to superpose the one with the other, even in 3D space, they do not fit together. There is nothing common in those 2 graphs that would offer the possibility to put one perpendicular to the other. The only common ground is the point zero. All the rest is pure contradiction. IOW I don't understand how one can put the i axis perpendicular to the Real number axis. The meaning of the product gets ambivalent: does 3i follow the rule of the Real numbers (3i is positive) or does it follow the rule of i (3i is negative)?

Yes, I see the difference now. Thank you for the clarification. That is part of my question. The multiplication rule for i looks to me completely incompatible with the multiplication rule of the Real numbers. As shown in my graph. 4. There is no common ground.

Well understood. I got confused by https://www.wolframalpha.com/input/?i=-i^2 And https://www.google.com/search?q=-i^2&oq=-i^2&aqs=chrome..69i57j69i64.5694j0j7&sourceid=chrome&ie=UTF-8 Why? You can invent it. What is wrong with this concept?

Thank you. That is not what I get from a search, even not in Wolfram Alpha.

I have combined 2 imaginary axis. The same way as I have combined 2 Real number axis previously. It is a different approach than combining Real & Imaginary as perpendicular.

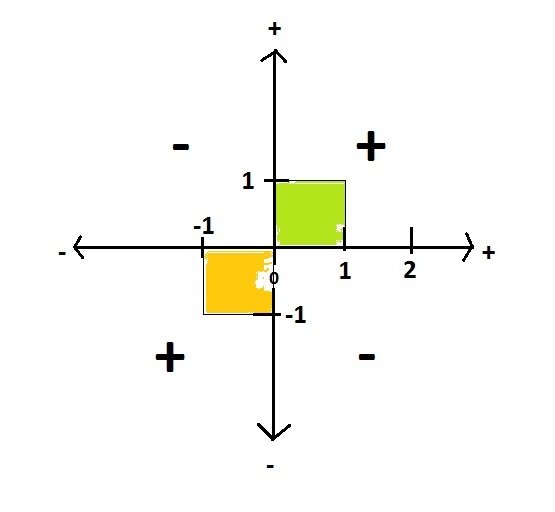
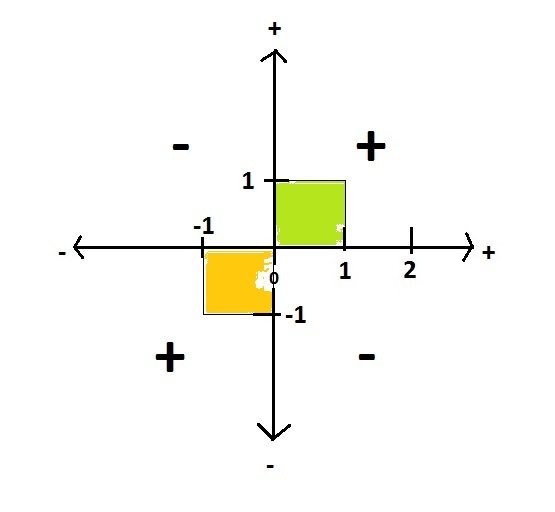
At the risk of being completely idiot here below something I wonder: Step1: the positive & negative on the number line. This above is a representation of the number line, the Real numbers going from zero to positives on the right & negative to the left. Step 2: When it comes to multiplication, we can show the sign rule in the following diagram. Where we have the product of 2 positives is positive. The product of a positive with a negative is a negative, the product of 2 negatives is a positive. Step 3: From the diagram above it comes out that the square of a Real number, positive or negative, is always positive. As shown below, the 2 squares are in a positive area. Step 4: Then we go to imaginary numbers (Complex numbers), in such a way that negative squares can be handled, as shown below. Where we see that i^2=-1 (the blue square). Question 1 is: where is the catch? Why is this diagram wrong? Why -i^2 (the red square) shows negative in the diagram? Although the correct answer is that -i^2=1 Question 2 is the following: what is the sign of 2i? Is it positive or negative? Do we follow the rule of the Real numbers, or the rule of Imaginary numbers? Question 3 is: how can you combine the Real number diagram with the Imaginary number diagram? Where is the common axis? The only common feature is a point: zero.

Today I learned about the Ashtiname of Muhammad

no comment

100 years ago somebody made the claim that Time & Space are intertwined. Spacetime is the thing to figure out what it is. Time by itself provokes a circular definition. Space by itself provokes also a circular definition. One can describe distance in terms of time: the distance one walks in one hour (the parasang). I am quite sure that one can also describe a duration in terms of distance*. Also, thanks to this "someone", one should focus over a quantity that mix Time & Space, called velocity. Because "someone" has made the remark that some elementary particle (the photon) not only has a constant velocity, but cannot even exist if it has not this velocity. Which is totally mind-blowing. * the Light-Year. As to the Time Flow, my idea is that it does not work that way. The objects "flow" in Time (& in Space). When you sit on your chair doing nothing, you still get older. In my view, it means that some kind of "motion" is taking place without you being able to see it. No external "time" is "flowing" over you.

That is the reason for "War on Terror". The U.S. are constantly in a state of war.

From what I read it remains an open question. There is an outstanding paper but in French http://culturemath.ens.fr/histoire des maths/htm/Verdan/Verdan.htm Lot of information and no answer since the author has exactly the same question: Encore une fois, il y a peu d'arguments qui permettraient d'établir l'existence d'une ou de plusieurs numérations antérieures à l'adoption de l'alphabet. Est-il toutefois irréaliste d'envisager cette éventualité? Une société analphabète peut très bien se servir d'un système numéral simple. ( Once again, there is little argument that establish the existence of one or more pre-alphabet counting system. However, is it unrealistic to consider this possibility? An illiterate society can very easily use a simple numerical system.)

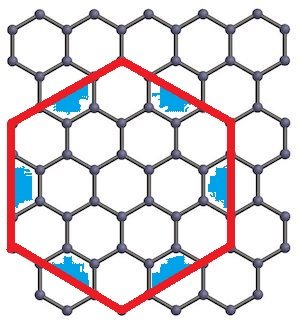
You cannot completely fill an hexagon with smaller hexagons. As stated above by Strange, the shape has uneven edges. When you reach infinity the blue areas get infinitely small but they are also infinitely many. Intuitively their area should reach zero.

[continued] Here a multiplication from Eutocius manuscript. Left in Greek, right in today's numerals. Don't ask me what's about...(it is 3013.75^2) https://el.wikipedia.org/wiki/Ελληνικό_σύστημα_αρίθμησης#/media/File:Multiplication_Eutocius.jpg And for once, the wikipedia pages for Greek numerals are different in English, Greek & French (interestingly it is not the usual copy-paste).

I learned something today. I knew about Escher but I didn't know about Penrose tiling.

Like laminar flow reversal. Mesmerizing.

You are overestimating my knowledge. However, from my knowledge, ancient greeks had no independent numbering system, they used letters. Alpha for 1, Beta for 2, a.s.o.( it gets weird after some letters, a system still used today in certain circumstances in today's Greece). most ancient cultures used letters for numbers. This situation has the result that any word can be translated in numbers. That is the origin of numerology. Any text can become a set of numbers. We got free of that after the invention of arabic numbers. From that point and after we all should have thrown numerology in the waste basket (together with astrology). But for whatever reason some of us didn't.

Yes, time for thought. Generally speaking I find that one cannot use any living system as an example of physical process. Life is totally weird. If you examine physical systems (out of Life), you may come to the conclusion that birth & death never happen. Once you introduce living elements yes birth & death do occur. As about time, one must admit that most (if not all) physical laws are time-symmetric. To me, Time is not an external thing. It is not a kind of wind that flows around us. Time is the impression we get while moving through. We are the ones moving. We are the ones who get old. The bizarre thing is that even when you don't move an inch, you still get older. You still "move" though time.