iwfc87

I know what inverse functions are, but how do I find an inverse of something like this: y=(e^x)/(1+e^x). What I thought of doing which I'm not sure about is: y(1+e^x) = e^x y+ye^x = e^x (y/e^x)+y = 1 1/e^x +1 = 1/y e^x = y-1 x = ln(y-1) I think what I've done is ridiculously wrong..but yeah...

Hello hello I've got 2 problems here which are based on the same welded slender bar. I've thought about it for ages, but I'm clueless on what to do. Any help will be much appreciated.. Cheers.

Well I do, but I'm not sure how to apply it here. I've attached what I've done. From then on, I'm clueless. I'm trying to get it in the standard form of (x+c/a)^2+(y+d/b)^2=1.

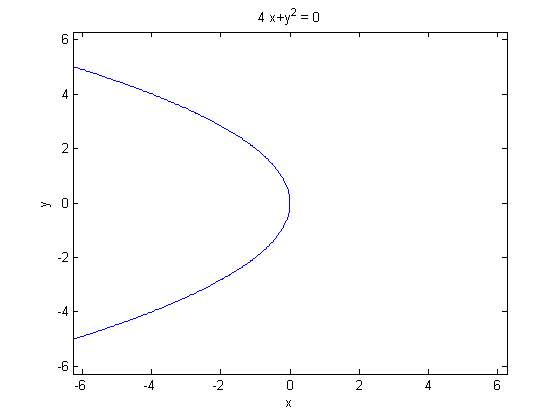
Apparently the equation [math]d_L /d_F= e [/math] should be an eclipse. I haven't quite got that. I get something nasty and gross looking like the equation below; which isn't quite an eclipse upon plotting. Have I done somehting wrong here :S? (plot is when e=1).

Yes it is. Thanks a lot. I was jsut utterly confused with the question. And the graph thing..whoops..my bad.

Hey all... Got this math problem. I've attached a the problem below and what I think the question looks like below. Other than that, I'm lost.

Heres a problem I've tried doing for ages but I can't quite get it right The answer is *apparently* approximately 10.8 degrees. Heres the question and a diagram to help visualise: Three smooth cylinders are stacked up in a trough as shown in the diagram below. Each cylinder weighs 400N and has a diameter of 125mm. Calculate the minimum angle theta which will support these cylinders in equilibrium.

Well, a continous function at a point is one at which the point is an element of the domain and the limit is equal to that of a function, but the question I *think* means the function as a whole, which I'm not sure of. As far as my knowledge go (baby knowledge) a function is continuous if you can draw it without raising your pen, but that's does not suffice I don't think. Apparently part (b) involves the "squeeze thereom" according to the lecturer, but I'm not too sure as I don't see what the function is being "squeezed" in between. Cheers.

Hence I am clueless. The subject is Calculus & Linear algebra and I think it's talking about functions (limits, continuity, blah blah blah). It might mean defined function?

Hey guys, well, my math problem is below and I need help on it: Determine the maximal subset of R(real numbers) on which the following functions are (i) defined (ii) continuous [math] [x] [/math] is a Gauss bracket of [math] x [/math]. Defined to be the greatest integer (Z) not greater than [math] x [/math]. Eg: x=1.7, [x]=1

Hello all, Well, I've been making soap in the lab using olive oil, NaOH and ethanol. I was just curious, what is the purpose of the ethanol in the experiment if the reaction is between mainly olive oil and NaOH is involved during the saponification process? Cheers.

Whoops..my error..but yeah. So how am I going to solve the problem of calculating the % content of nitrogen in the fertiliser if I have so many different volumes and numebr of moles and all??

Hey all, I think I need a little help cause I'm a little confused. Well, heres the case: I'm trying to find the % content of Nitrogen in fertiliser by mixing an ammonium sulphate(NH4)2 SO2 fertiliser solution with a known volume of NaOH and then titrating it with a known concentration of HCl. From the equation, if I'm not mistaken, the number of moles of NH4 OH produced would be the same as the NaOH (calculated from a known concentration) 2NaOH + (NH4)2SO2 => Na2SO2 + 2NH4 OH This solution was heated and cooled, and then titrated with HCl and the volume required to change the colour of the indicator was recorded. I'm assuming the important part of the equation above is 2NH4 OH. Hence the equation during the titration would be: HCl + NH4 OH => NH4Cl + H20 As the number of moles of HCl required to neutralise the solution is less then the number of moles of NH4 OH, I assume that there is an excess of NH4 OH. So I then used this smaller number of moles in my calculations. To me..I think this is the stuff up, as if there were an excess, the solution would still generally be basic. Would this be right or have I made a stuff up? Please do guide me..I think I'm really lost..

This might sounds crazy, but does anyone know the surface tension of concentrated dishwashing detergent?? I've tried Google-ing, but I can't really find anything. And also, how are droplet volumes/sizes affected by surface tension? Thanks.

I'm back and I'm stumped. Well..what's happened is I was thinking of Van de Waal forces, and as water has Hydrogen-hydrogen bonding, why does it have a larger diameter than that of olive oil or motor oil when dropped from a range of heights? I also learnt that the greater the surface tension, the rounder the droplets would be on departure (at least I think ), but does that mean a smaller volume of liquid leaves as well? Uh oh..I think I'm really lost now. I cannot seem to relate my data with each other. You see, I've known that motor oil has the lowest surface tension than all my other liquids (water, olive oil and dishwashing detergent), but the problem is, it drops the fastest (understandable as it had the least volume/drop and a moderate mass/drop..but also means more KE on impact), has a dispersion van de waal force (weakest..i think), but despite of these, it manages to maintain the smallest droplet diameter. In fact, nearly constant at all heights