Tom Booth

I did not see that request, as I said I have some backtracking to do. Anyway it's in the public domain. Copies can be downloaded from any of dozens of sites. Wikipedia has an online text which is useful for reference and searchable: https://en.m.wikisource.org/wiki/Reflections_on_the_Motive_Power_of_Heat What I referenced is in the appendix A. "extracts from unpublished writings of Carnot". (My apologies to everyone for any other comments I haven't gotten to yet.)

Context? I agree that generally speaking there are known and to one degree or another controllable loses, friction, vibration, conduction. General unwanted dispersal. Disappearance of some 80% or 90% to some specific place (the "cold reservoir) aside from all that (ignoring friction etc.) each cycle is completely ludicrous. Instead of the 1:1 ratio experimentally verified the Carnot ratio is 1:8 or 1:9 in our little heat engine experiments. A glaring discrepancy that I think needs some verification.

Well, I think the idea ( kinetic theory of heat) is that the atoms (let's say helium or perhaps hydrogen, commonly used in a Stirling engine as working fluid) each atom has a center of mass (translational kinetic energy) and are moving and colliding with each other, with the chamber walls and in an engine, with the piston. There is a 1:1 ratio between Joules (heat) and Newton meters (motion) So heat (transfer of energy) on an atomic level is a transfer of motion. There are other kinds of motion of the atoms, rotational etc. But these are relatively static or tend to cancel out on the whole. The only significant conversion (joules to newton meters) taking place at the gas/piston interface where the gas collides with something that can actually move and respond to the impact allowing a transfer of motion (kinetic energy) between the gas particles and the piston. One can imagine the billions and billions of impacts required per second in order for the infinitesimally small gas atoms to displace the gargantuan mass of the piston. I still have some additional comments I need to backtrack and answer in sequence.

Ah, finally worked my way down to the question I was really looking forward to addressing. Same question Carnot asked in his unpublished notes. If heat is just another form of kinetic energy that can be directly transfered, why should cold be necessary? Why does lowering the temperature of the cold side improve performance of the engine? Why do we need a temperature difference at all? My tentative theory stated somewhat figuratively or by analogy would be that making the working fluid colder gives it more room to expand. The container volume is fixed, so at any given temperature expansion is limited to the distance the piston can travel, restrained by being connected to a crankshaft. (Excluding "free piston" type engines from the discussion for the moment). Cooling the gas causes it to contract more, increasing it's potential to expand. Does that require an outside source of cooling? Certainly, initially. But once a new baseline is established and the engine can start producing more rotational force, more work output, then the cold side only provides a kind of stability or thermal buffer of a sort, but the engine no longer transfers heat to it, and it runs the same as before the ice was added, transforming all the heat supplied into work again. This is why load balancing is important. The gas expansion is limited to the distance the piston is designed to travel, once that limit is reached, if too much heat was supplied that cannot be converted to work output, the bottom dead center is reached too early so instead of having room to convert all the heat into work output, the engine WILL certainly begin to build up excess heat In other words the extra cold being present does indeed help the engine run better, but the ice placed on top doesn't constitute a lower temperature sink for the heat to "flow into faster" it doesn't "increase the gradient" or "downhill slope". The cold or a temperature difference generally just provides a starting point for expansion, and adding ice just provides more leeway for expansion and contraction generally, it doesn't mean that the ice is continually taking in more of the heat, or taking away the heat faster. I sometimes use the analogy of a trampoline. If you have a low ceiling you can't bounce very high. But also if the trampoline is not raised high enough off the floor, you can't bounce very much either. There will not be enough room under the trampoline to bounce without hitting the floor. The throw of the piston creates a ceiling on how far the piston can travel out and so also how much the gas can expand, and the cold is the floor which has to be low enough to provide room to bounce also. What keeps the engine going is "adiabatic bounce". An oscillation, that just needs enough heat to match the work output and loses to friction and other parasitic heat loses, but NOT losses to the "cold reservoir". If you notice, I always put these archaic terms in Air Quotes to basically shorthand saying so-called (in quotes) "reservoir" etc. Possibly some new terminology IS in order, so rather than in quotes so-called "cold reservoir" we could just call it floor or something. I've been calling it the ambient baseline but that is not accurate when ice is added and the floor or starting point for expansion is lowered below ambient. Thanks for asking a most pertinent question.

The word "flow" (aside from other thermodynamics terms we could talk about) among other possible meanings/applications can refer to the flow of water down a hillside in a stream or river, or a flow of traffic on the highway. I have no issue with the word itself just how it is associated with heat and the implications on a subliminal level of all this archaic terminology: flow, reservoir, etc. Directly relating the "flow" of heat through a heat engine to the flow of water over a mill wheel and so forth. A flow of water from a height is caused by gravity. The flow of cars on the highway, or people down a sidewalk or corridor is self motivated. Maybe "self motivated" is not the best way of putting it, but cars are not pulled along by an outside "gravitational" force, they have their own motive force or kinetic energy or motion, they are self propelled. Why is that an important distinction to make? Well, gravity holds water down to earth in a "reservoir". And gravity causes water to flow in one general direction: down. Gas particles sealed inside a Stirling engine aren't going anywhere. If they are zipping around or vibrating or expanding and contracting it is all due to the energy they are carrying around with them, not something somewhere else compelling them to "flow" anywhere. So there is a general dispersal of kinetic energy in a quantity of gas from the more energetic particles to the less energetic particles, setting aside infrared waves or other possible quantum phenomenon for the moment. In his unpublished papers Carnot wrote; paraphrasing, that if heat is actually motion, that would explain everything, the action of Joules calorimeter etc. But if that is rely the case, to quote (in translation): Difficult indeed. If we have a gas enclosed in a sealed container with one piston and cylinder, all at thermal equilibrium, then introduce some additional heat into the gas, there will be billions upon billions of collisions per second, some of which contact the piston causing it to move in the cylinder. The gas has no need for a "cold reservoir" outside this container anywhere to "flow" to like water down a hill to a lower "reservoir" I keep repeating the language so as to bring it into awareness and point out the influence it has and it's origin.

Skip

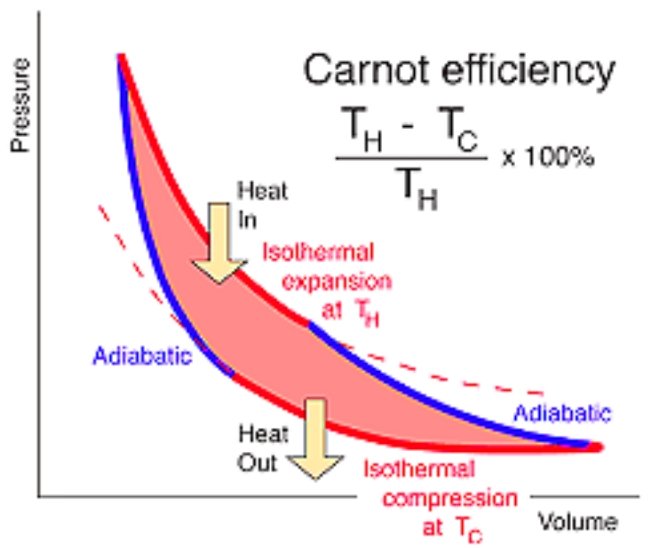
Again, I apologize for jumping to conclusions in that I assumed you were talking about the "Ideal Carnot Cycle" I've taken some time to revisit this post and review what you wrote compared with the Wikipedia article. Unfortunately, IMO, the description in the Wikipedia article is also wrong as far as having any relevance to how a real Stirling engine operates. Is it an accurate description of an "Ideal" Stirling engine? Maybe, I don't really know. Out of who's imagination was this "Ideal" concocted? I did some perusing through the original patents of Robert Stirling. Maybe I missed something but I didn't find anything I could put my finger on that related to this "Ideal" mode of operation. What is generally agreed upon by "experts" I've known on the Stirling engine forums for years, some passed on now, is that so called "Isothermal" processes in a REAL engine are not possible. The portion of the Wiki article cited also does not include any description of the action of the displacer, normally advanced 90° ahead of the piston (in a real engine with a crankshaft) etc. I have no particular interest in debating the issue at length to prove anybody right or wrong, I could really care less. I'm interested in Real engines I can build not imaginary theoretical "ideal" engines based on impossible cycles arising from some pipe dream. Anyway taking one leg of the cycle (your description): This is simply false. Well, is it an accurate description of an "Ideal" Stirling Engine, backed up with references? Probably, I'll grant you that, but it has no correspondence with how a REAL Stirling engine operates. In a real Stirling engine, during compression, which is really neither isothermal nor adiabatic but something else that I don't think any thermodynamic terminology could describe, but let's just go with adiabatic for the moment. The gas, during "compression" is really contracting. Well what actually causes Air to expand and contract? I mean actually? Heat is added to a gas and it expands, or if confined, tries to, creating pressure. We know what it does, it expands, but how? Do the electrons orbiting the nucleus move to a higher orbit? Does anyone actually know? Any quantum physicists in here? Let's just say that for whatever reason the gas needs more room. But pushing the piston out the energy previously added is used up 100% so the gas then drops back down to the original lower energy state. It no longer requires the extra room. The piston gets sucked back down the cylinder (or if anyone prefers, atmospheric pressure pushes the piston back.) This collapse back to a lower energy state looks like isothermal compression with "heat rejection" but it isn't. Remember the graph, at BDC, full expansion the gas experiences a sharp drop in temperature. So a cold gas is contracting while continuing to collapse back to a lower energy state. This may look isothermal "with heat rejection" but that is not possible. A cold contracting gas cannot "reject heat" to any adjoining hotter body. It's colder than both the hot and the cold heat exchangers so how can it transfer any heat to either? When "compression" (contraction) is about half way completed the displacer shifts the gas over into contact with the hot heat input heat exchanger. Compression continues as more heat is being introduced simultaneously. So does this really make sense: "For an ideal Stirling engine maximum compression occurs at the end of the cooling cycle with the working fluid at cold reservoir temperature TC." No, it is actually closer to the temperature of the hot "reservoir" due to the displacer shifting the working gas over into contact with the hot heat input plate. With the added heat of compression. Remember the ACTUAL READINGS? the temperature exceeds the temperature of the hot heat exchanger at full compression. This, in actuality resembles an Ideal Carnot cycle more closely than this so-called "ideal Stirling cycle" in the Wiki article dreamed up by whom, I have no real idea. You can take it or leave it, but this is very hard won information distilled from years of careful observation. All this "ideal" nonsense, in my mind, goes straight in the "circular file". As far as I'm concerned, any talk about "Ideal" anything in here is "off topic". We are looking at REAL engines, actual experiments, real measurements. Not that I'm going to report anybody or anything of that sort. The question is, does this Carnot fantasy "efficiency limit" or "upper bound", whatever you want to call it actually mean anything at all in the real world? Does an engine that utilized just 21% of the heat supplied to it, instead of the 20% predicted by the "Carnot coefficient" 😆 Or that "rejects" just 79% of the heat supplied REALLY overturning some physical "LAW" of the universe ? That's a pretty big number (80%) Seems like a lot of heat that is just "unavailable" for no good reason whatsoever. I think I'd like to check on that. Do some actual tests/experiments. That the 80% on the absolute scale below TC is unavailable I can live with but 80% of the heat I actually put into the engine? No Way. "Extraordinary claims require extraordinary proof" and 80% of the heat supplied being whisked away without explanation, for no good reason seems like an extraordinary claims to me, especially when such a supposed large proportion of "waste heat" is apparently undetectable. Are we supposed to just swallow all this 1800's archaic steam engine theorizing without actual proof? I mean is this really "accepted science"? I still haven't seen any historical account of who originally verified any of this experimentally. So, maybe it works for steam turbines? I don't know. People actually use it? I doubt it. But even if they do, how does that prove anything conclusively? Did he? I must have missed that. I took the liberty to correct a minor typo ("that" to than, if that's not ok let me know) That is a good point I think, but not for the reasons you follow up that with. How does that follow? Besides, a gas DOES hide it's "internal energy" I think, if that's the right term for it. I mean it has been heated up from ABSOLUTE ZERO or thereabouts. Right?

Skip, irrelevant semantic knit picking IMO. A silly argument. "Carnot efficiency limit" is a phrase in common usage in learned papers (Science direct etc.) Not "garbage". I did not invent the term, the phrase or the application. Unlike you I actually read many of the papers that come up with that search. You consider that a "personal" attack or something, well sorry but I told you you are better off if I just ignore such nonsense and move on, but then you have a meltdown and want to go crying to mommy and report me for ignoring you and threaten to have the thread shut down. You asked for it. You got my honest appraisal. Your protestations about my usage of a common phrase in thermodynamic literature speaks to your ignorance of the subject not my misuse of common terminology Time to get some work done. Sorry about additional unanswered posts (from anyone) I haven't read yet, I'll get to them later whenever I find some time. Before I go to work, I just want to say that this is a puzzling phenomenon if heat is not actually passing through to the ice, why does the ice cause the engine to run observably much better. It certainly appears that the increased ∆T results in increased efficiency. The conventional, or generally accepted explanation is that the ice increases the temperature "gradient" or slope, allowing the heat to "run downhill" to the ice faster increasing the "flow". Seems reasonable. But after years of observation, taking measurements, doing experiments etc. I've arrived at a different explanation. I don't have time now, but I am very anxious to get back to and address this particular point of interest. Unfortunately, I also have other matters to attend to at the moment.

Who says any word must be limited in use to some one specific application? Your assertions here is bewildering to me. Try using an internet search engine (ie Google et al) and perform a search for "Carnot efficiency limit" in quotes. There is no end to thermodynamics and general scientific references using that exact phrase, routinely the majority of which are applied in the same way I have been doing here and to the same formula. You are apparently not very well read on the subject of thermodynamics is about the only conclusion I'm able to draw from your above attestation. LOL Read, but skipped as not calling for a response. (So Studiot does not feel ignored and petition to have the thread closed).

Seems we are in the same page. A "coin" is a "thin piece of metal" commonly used for monetary exchange. On the WWW spanning the globe I understand there are different dialects, language barriers, some might be using translators. I'm American my wife is from "down under" and we often can't get through the day without some mix up. On an international forum, X10. It's to be expected, can't be helped really. I'm one person trying to respond to comments and questions from half a dozen other people from I know not where. An occasional misunderstanding is to be expected and is inevitable. Add cross posting, late edits, stupid spell check programs, typos, the existence of words with dozens of shades of meaning, different in different regions etc. It's something of a wonder we can potentially collaborate on some experiment at all. We are at an early stage of at least making some attempt at cooperation and mutual understanding here. That seems like a major breakthrough to me. Thinking on it a bit more, the cold heat exchanger of the engine(s) are simply thin sheets of metal. A plate could be removed from the bottom of one engine and the other plate shared. That is, the two engines would both be mounted on the same cold heat exchanger. In fact, on the Stirling engine forum we have contemplated eliminating the cold plate entirely. As someone on the forum said, this would allow the mounting bolts to pass from hot side to hot side without contacting, and potentially conducting heat to the cold center plate. Maybe have a cold disk suspended between the displacers. Theoretically (my own tentative theory) no cold object would be required if the two engines could be driven mechanically for some time with an auxiliary motor, if they are truly acting as heat pumps. The shared bottom (bottom/top) plate would be chilled by running the engines as heat pumps. Edit: and of course temperature probes. Probes everywhere. invalid for any real world heat engine. I certainly did read that. You also made the claim: I'm not convinced that you have actually established this claim at all. There are untold numbers of educators teaching students that the formula does very well apply to every engine ever built and every engine that could conceivably ever be built. There are textbooks, tutorials, videos, example problems etc.doing that very thing. Applying the formula to real every day situations and engines of all types. Yes the Carnot engine is imaginary but it stands as a very real theoretical LIMIT to each and every REAL engine that ever existed or ever could exist. I think this is basically very true IF interpreted strictly on the absolute scale. Raise the temperature to supply heat 10% on the absolute scale. In that case the temperature can only be brought back down the same 10% to the same ambient baseline temperature. The other 90% down to absolute zero is unavailable. Makes perfect sense. That only 10% of the 10% is available is unsupportable and has no basis in reality. It does not even apply to the imaginary Carnot engine itself. It is a misunderstanding and misapplication of the formula IMO, that has been happily transmitted down through the generations. There is no reason why raising the temperature 10% on the absolute scale should somehow magically render 90% of the added heat locked up somewhere or swept away to the mythical "cold reservoir". Feel free to propose a better way of calculating real efficiency but that does seem to be veering off topic a bit.

Ok, so if I drop an object in a vacuum, that's an actual possibility. It could be proven that even without air resistance there is a limit or potentially real measure of how things fall in the absense of air. A frictionless surface is actually achievable. Magnetic levitation of a superconductor. Not a surface exactly, but it certainly approximates a frictionless surface. Perfectly elastic collisions between gas particles seems real enough to me. Carnot efficiency is, IMO a completely arbitrary construct invented based on a fallacy regarding the nature of heat, has no actual physical basis whatsoever, has never been empirically tested, verified or demonstrated in any way shape or form, it's just a hold over from the caloric theory. There is no caloric. There are no pools or "reservoirs" of this supposed fluid, it is admittedly all complete fantasy. No falling down like a waterfall to a "lower" temperature. Heat is not "flowing" through a heat engine. It's all a misconception an illusion a mistake. That's what I honestly think anyway. I've been doing experiments looking for the "waste heat" supposed to be emanating from the cold side of my Stirling engines and there is scarcely anything there. There is no rational or material reason why a ratio based on a temperature difference determines anything. Anyway the power of a waterfall depends on the height AND the quantity of water, like volts and amps. What Carnot actually said was that the utilization of heat depends on only the temperature difference and the quantity. Carnot never said temperature ONLY period afaik, that was somebody's misreading of a bad translation or something probably. There is no historical account of this formula having ever been proven that I could ever find. It has no basis. Not the way it's being taught anyway.

Not just "imaginary" within the realm of possibility. The processes as described are literal impossibilities. There is no possibility of an engine using "isothermal expansion" to draw heat away from some object while maintaining thermal equilibrium with that same object. Certainly not in the time a piston moves from BDC to TDC. What's the point of contemplating something that has no correspondence to the real world. No practical application. It only had a seeming reality if heat were actually a fluid you could draw out as if sucking up gravy with a turkey baster. Today we know better. Let's entertain the Carnot scenario (as typically interpreted in online tutorials, textbook problems etc.) Two heat engines. 20% Carnot efficiency (determined by the ∆T, each sharing a finite "cold reservoir" (the ice or cold object between them. If it is true the 20% efficiency figure can be applied to supplied heat above the baseline ("baseline" = everything at some one ambient temperature before the quantity of heat in question was added) we put 10,000 joules of heat into the engine each cycle in some measurable way, watts of electricity or whatever. After one cycle 8,000 joules of "waste heat" should be found added to the sink helping warm up a cold plate, melt ice or whatever. Idle engines should transmit the heat the fastest. 1 engine running should transmit less heat (because 20% is converted to work) 2 engines running should reduce the heat input more if the 10,000 joules is divided between them or transmit more if each engine receives 10,000 joules and "rejects" 8,000 each to the same sink. But In each case the ice should melt quickly as each engine is only reducing the heat flow marginally. If on the other hand the engines are converting a much higher percentage of the heat, more than the Carnot limit predicts, then with the two engines acting as "insulation" with the ice (or whatever cold thing) between them, the object should require a very long time to heat up or melt. In other words, if there really is a kind of slight refrigerating action by the engines, nothing (no engine at all) or non-operating engines should melt the ice quickly. One engine would be like a refrigerator with the door open. The ice will still melt, but maybe aittle slower. Two engines together would be like two refrigerators with the doors off but using each other to enclose the refrigerated space. The two engines "helping each other" should produce a dramatic lengthening in time before the engines ever stop running, before the sink fills up with heat. But only if the Carnot limit is a complete fallacy. If the Carnot limit is true, and at least 80% of the heat supplied to the engines passes straight through to the ice, then putting the cold sides of the engines together should 't make much difference. If the Carnot limit is a rather grotesque error or misunderstanding and in reality virtually all the heat supplied can be converted to other forms of energy, which is no violation of conservation of energy, there should be a dramatic lengthening in the time it takes for any heat to reach the sink cradled between the engines.

What do you mean by "ice-less"? The "colder than ambient" temperature of the working fluid is at best a brief "flash in the pan" near full BDC. Without insulating the cold side of the engine such a brief instant of sub-ambient cold would be completely overwhelmed by the immediately adjacent ambient heat, being generally or probably undetectable by slow responding thermal measuring instruments. Carnot's original declaration, and I can only call it that, not a scientific theory was that ALL the heat going in was "transported" through the engine, like a bucket of water carried down by a water mill wheel. Later this was modified, IMO arbitrarily to harmonize more closely with new findings. Heat could be converted to work, and also the absolute temperature scale came along. If Carnot ever talked about the zero of temperature he meant 0°C Personally I think this efficiency limit equation attributed to Carnot, whomever came up with it, and I haven't been able to say for sure who, probably originally meant the engine could take in a quantity of heat at T-hot and convert that quantity into work only as far as bringing the temperature of the working fluid down to T-cold or the surrounding ambient or coldest "reservoir" available. Period. That makes perfect sense to me as a general rule of thumb. But the modern interpretation seems to be that if a quantity of heat is taken in at T-hot, it can only be converted into work as far as bringing the temperature down to... ... To what? Not T-cold. Instead, if the distance between T-hot and T-cold happens to be 15% of the distance down to absolute zero on the Kelvin scale, then with that ratio in hand we are going to now say that taking in a quantity of heat at T-hot, we can only convert a small portion of that quantity of heat into work. So the temperature can only be reduced something less than 15% not on the absolute scale now, but only 15% of that limited quantity of heat actually added. By what actual physical mechanism do we make that transposition? Someone got the percentage of the absolute scale mixed up with a percentage of the actual heat supplied. If T-hot is 80°F and T-cold is 0°F without heat "rejection" somewhere we can only reduce the working fluid what? 12°F and the temperature must be reduced the other 68° through rejection of all that heat to the sink. Our ice or whatever. Why? So if the ice is a small finite "reservoir" it should melt pretty quickly, if we have to put all that waste heat into it in order to bring the temperature of the working fluid down another 68°F in the fraction of a second it takes for the piston to round TDC or BDC or wherever this impossible "rejection" of heat to the "cold reservoir" is supposed to happen. If ALL or nearly all the heat added can be utilized to bring the temperature all the way down to T-cold then how do we actually "reject" any heat to the cold reservoir at T-cold? We can't. They are the same temperature! But that is what the "Carnot cycle" proposes we do. How? Why, we can utilize an isothermal process. We just have to very very slowly move the piston. Infinitely slowly, so that no temperature changes take place. After an eternity of time, eventually all the heat will transfer one way or the other. No it won't. We are suppose to inject this rather large quantity of heat (relative to the heat converted to work) nearly instantaneously over an eternity. It's so much nonsensical bullocks it could make your head spin. According to the Carnot limit equation. That is what we are trying to validate. You haven't clarified what you mean by "invalid". Do you mean it is only a limit and not a precise measure? As is already universally understood afaik, or it is complete hogwash? What words or phrases, sentences or paragraphs exactly can't you follow? Of which post? What is hard to understand or complicated about putting some cold object between two engines?

Let's say we dip a coin of known heat capacity into liquid nitrogen and put the coin in a circle cut out of a silicone mat the same thicknes as the coin. 1) Put that between the two engines. Not running. 2) Repeat with one running 3) Repeat with both running What would be the outcome in order of melting (or running) time?

Well thanks for clarifying, but you actually did, by hitching you wagon to Studiots post: That was how your post opened. Throughout you never mentioned any other cycle or engine specifically, so it seemed you were adding to. Anyway my apologies, I assumed, from the way the post opened as an addition to Studiots, that it was about the same. But thanks for the clarification. No, I did not see the first part. Let me be clear, I'm not attempting to prove or advocate for "perpetual motion" here. Just something Less Than the reciprocal of the Carnot efficiency. The inefficiency or heat transmitted through to the sink. In this setup, that would be what? Assuming an arbitrary, but realistic ambient (room temperature) outside and inside the box of 75°F and an ice cube or whatever at typical household freezer temperature at 0°F gives us a Carnot efficiency of what? (Maximum unapproachable efficiency for a real engine of course, not actual efficiency I think that goes without saying) 14% (approximately) So, we get a minimum heat pass through of 86% but we can assume that 14% efficiency is way too generous. So probably something more like 90% or more heat pass through. Infact we have Two engines pushing 90% of the heat they take in straight through to the ice, Each. So, can we assume anything regarding how fast the ice will melt? Are we completely in the dark about how much heat might be entering into the two engines? Maybe we can't KNOW, not entirely without some really exacting instrumentation and data recording, but generally I think it fairly safe to assume the ice would melt pretty quickly. What would be the expected outcome? A perpetual motion machine? Hardly. As for the other question, I assume you already received the references. There is the drinking bird of course, which I'm pretty sure everyone here has seen but also there are heat engines that can run on the ∆T from simple evaporative cooling. Nothing remarkable in that IMO.

So are you saying that the answer to the opening question is NO. Is (the) Carnot efficiency [limit] (formula) valid? No? My impression has been, that as a limit your answer(s) would certainly be "yes". Even perhaps an overly generous approximation. I certainly never imagined it was an exact representation. But certainly as a limit on the actual efficiency of any REAL engine it is considered absolutely valid. If therefore, no engine can exceed that limit, no engine can exist which does not emit "waste heat". I've watched dozens of tutorials and solved dozens of sample problems on how to use the Carnot efficiency equation and what it means in terms of real world applications involving joules of heat in and joules of waste heat out and joules converted to work. So, what do you mean by "invalid".

Heating and cooling imply, or more than imply a transfer of heat. Do you agree? So these statements are incorrect in their entirety as well as the conclusion stated. Maximum compression and maximum expansion are both preceded by adiabatic processes, in the ideal Carnot cycle. So I would not say that the Carnot cycle is "opposite" to most heat engine designs. Far from it. Most heat engine designs are intended to approximate the Carnot cycle as closely as possible. Some come close, some don't, but "opposite"??? Can you provide us with an actual example of a heat engine design that is the opposite of the Carnot cycle, and what is the relevance of all this? Have you ever actually examined an "ideal Carnot cycle"? I'm afraid it's more than that. You have the Carnot cycle turned completely upside down and backwards then declare this is the opposite of most engine designs. You have completely ignored the adiabatic legs of the cycle which at full compression resolve at T-hot (not Tc) and at full expansion resolve at T-cold (not Th) as with real heat engines. The main difference between a real engine and a Carnot engine is in the fact that a real engine is nearly all adiabatic expansion and contraction as isothermal processes take place quasistatically (infinitely slowly) which is not possible in reality. There is a company claiming to have developed a near isothermal heat pump involving dipping numerous thin rods into fluid to effect compression but this is not typical.

So c as in Vc stands for Volume compressed? c=compressed (not cold) And the H in VH? (Or Vh lower case. Both appear, so this too is confusing.) Is your H the same thing as your h?

I think perhaps Studiot intended to continue his outline and I did not wish to interrupt. One important point he made though, that I would like to highlight: Regarding your "fixed volume range" I'm not sure about the assumption behind you equation: It might help, well it would help me anyway, in following your reasoning if you could clearly define your terms. Vc I assume represents the volume of the gas at is lowest temperature? V cold? VH the volume of the gas at its highest temperature? V hot? Or is that Enthalpy. And V, what does this represent? The mean? So the volume is greatest when the temperature is highest? The volume is least when the temperature is lowest? What kind of engine are you referring to? You do realize, generally speaking: compression decreases volume and increases temperature. Expansion increases volume and decreased temperature. So in an engine Vh > Vc. If your initial assumption is incorrect, there is no need to consider what follows from that.

Sorry if I'm a bit of an optimist and don't entirely share that outlook on life. Anyway, I spent $60 and I think the experiments will be fun to watch however it turns out. I think it (the twin engines) will run for a good long time. In my experiments so far, the engines running on a cup of hot water keep running for about 3 hours tops. On a cup of ice, 33 hours. So far, with imperfect insulation. I know, heat capacity and all that. Truck is loaded so I'm on my way to the landfill. Still half a dozen other posts to respond to. Anyway you haven't really addressed my points, only pulled off the ignition wires, drained the gas tank and smashed the valve lifters. "See, it can't possibly run." Well don't worry, I'm a mechanic. Maybe I can fix it up. BTW, if you look at one of these engines, all the friction producing components are on one side. Running on ice, that's the hot side. So... Friction loses? Heat lost to the hot side is what? A bit of additional heat that either goes right back in to power the engine or returns to the heat source it came from. We haven't even talked about a regenerator, so far.

That's why we begin by using our big freezer plugged into the utility grid as a start point. I neglected to mention the ice or whatever is colder than need be to chill the engine on the cold side and the working fluid before moving the displacer to let in heat. Your scenario positions everything in the most inopportune way. The action of the displacer is rather essential to the operation acting as a kind of heat valve, to let heat in only at the critical moment. Like a batter waiting for the pitch.

Today I've been removing trash from the basement that is in the way of my running wires and need to hurry and get to the landfill before it closes soon. There has been a flood of posts while I was working I'll have to read later and respond to. Not ignoring anyone, just another busy day.

What happens to the best of compression when atmospheric pressure pushes the piston back. Well, the gas is in the process of collapsing. The gas absorbs the heat raising the temperature back up to the temperature of the hot side by the time it is, maybe 2/3 of the way back. At this time the displacer moves off the "heat source" side. But where did the heat actually come from? Atmospheric pressure? At the last moment the input heat and the "heat of compression" collide, but the piston has also acquired momentum and keeps going compressing the gas further to a temperature even greater than the "heat source". The bat meets the ball so to speak. Grand slam. The piston goes out with increased velocity. Has any heat reached the "cold reservoir" yet?

I can see your point to some extent. It makes sense and I think I understand your point. But... Let's visit the two engines together using the same piece of ice between them as the lower cold reservoir. The two engines first exist at equilibrium with the environment. There is no hotter or colder "reservoir" correct? So we create a mock cold reservoir using our refrigerator to make a thin sliver of cold. Ice, cold metal plate, whatever. Now we have ambient heat entering the engines from both hot sides, but this heat cannot get to the cold reservoir any other way except through one or the other or both engines. Once the heat reaches the gas inside the engine(s) the gas expands and drives the piston(s) performing work and the heat "goes out" as mechanical shaft work. The engines are running. From my reading, I've come to the understanding that actually it is theoretically possible to convert 100% of the heat used in the expansion of the gas into work output. I've read this statement in many places. Is this statement not correct, that ALL of the heat can be converted to work on the outward "power stroke" ? So, consider this for a moment. If I push a car up a hill against gravity is not that comparable to gas expanding and pushing a piston out against atmospheric pressure? What if I use up all my strength pushing the car up the hill and collapse? Haven't I added potential energy to the car? Hasn't the expanding gas added potential energy to the piston? As a result of the expansion work the gas that did the work falls in temperature, like I fell down exhausted. What happens to the car now? What happens to the piston once the energy from the expanding gas has been exhausted? The car rolls back down hill. Does it not? There is a return to equilibrium. What about the piston, if 100% of the heat used to expand the gas has been converted to work and the temperature of the gas, and therefore also the pressure falls, the engine is left out of balance. Will there not be a return to equilibrium? The outside atmospheric pressure that the expanding gas was working against will push the piston back and equilibrium will be restored. What quantity of heat that went into the engine originally had not been converted? How much has gone into the "cold reservoir", our sliver of ice or whatever, between the two engines? None so far. But aha! The work done by atmosphere will heat up the gas and that heat will need to be removed. Right? Well, what temperature is the gas at the end of the power stroke? Hasn't it fallen to the temperature of the ice, or perhaps below? What happens to the car when it reaches the bottom of the hill we pushed it up adding potential energy? Does it stop rolling at the bottom of the hill? Atmosphere pushes the piston in restoring equilibrium to the system. Is it then possible to add another dose of ambient heat to drive the piston out again? Why not? My basic point is that there is no actual fluidic substance that was raised up flowing out of the engine carrying it's stored potential energy with it. The engine is hermetically sealed.

Well, "the potential energy of water" is different from the potential energy of a given quantity of heat. What does "the potential energy of water" (your usage of the phrase) actually mean? You are really talking about gravity, we are not decomposing water into hydrogen and oxygen gas molecules or some such thing along those lines using the water itself as fuel. Heat entering a heat engine is not a substance or liquid like water subject to a gravitational force that is somehow pulling the heat through the engine. The heat, as sensible, measurable "heat" that can be detected with a thermometer does not go through the engine, it only goes INTO the engine to be converted to mechanical work. The "work" goes out, the "heat" disappears and never comes out the other side as heat. At least not all of it, only some percentage of what went in. Taking the water analogy, the water would disappear while passing over the mill wheel.