Tom Booth

Of course "some" motion will be left. Otherwise the temperature of the gas molecules hitting the piston would reach absolute zero and cease to exist, or perhaps reduce to the form of a Bose-Einstein condensate, but we exist at 300k which is very hot already and we are not talking about utilizing "all the heat" down to absolute zero, just the added heat we supply to the engine. Some of the gas molecules, I believe, might indeed drop well below the ambient baseline. As in the Claude method of air liquefaction. (Which includes having the gas do work by expanding in an engine pushing a piston to reach cryogenic temperatures).

I respect Carnot. In the end he recognized the error he originally helped perpetuate and finally rejected the caloric theory and all that it implied. but unfortunately nobody read about that for many years to come. My contention is with the theory Carnot represents generally, not the person or any people.

"What do you mean by 'above the ambient baseline'?" I mean simply that the engine exists in an ambient environment (our earth atmosphere) at roughly 300° Kelvin. The surrounding pre-existing heat in the environment around the engine is what I'm calling the ambient baseline. To get the engine to operate additional heat must be added above the ambient heat in the surrounding atmosphere supplied by the sun. I don't agree with it (the interpretation) but the "carnot limit" is generally interpreted as representing a percentage of the added heat we supply to get the engine to operate, not all the heat, including the pre-existing heat in the atmosphere all the way down to absolute zero. If you object to referring to "heat" call it the kinetic energy of the surrounding air molecules or whatever you like, but I don't mean "temperature" There is certainly "heat" on a molecular level being supplied from the ambient environment. The engine is bombarded with hot air molecules bouncing off it continually on all sides, though the engine is equally hot, so the exchange is mutual. Mathematically the carnot limit is derived from the difference in temperature produced as a result of adding heat (raising the temperature) above the existing baseline of 300k. (Approximately, depending on location). If the carnot limit means anything, (what makes some sense) is if it is applied to All the heat down to absolute zero. Then the heat we add is the limit of heat that is available to convert back into useful work. All of it, not some meager percentage or ratio.

How could these working fluid temperature fluctuations take place? Well, it's simple. During the first part of the compression stroke the hot heat exchanger is blocked. During compression the temperature of the gas increases due to adiabatic compression. (We are talking about a real engine running at high speed, so isothermal compression is not actually possible). The displacer is 90° ahead of the piston. Half way into the compression stroke while the gas temperature is increasing the displacer uncovers the hot heat exchanger delivering a blast of heat to the working fluid as it is being compressed and already increasing in temperature by heat of compression. At full compression the heat from the heat source and the heat of compression combine and for a brief moment the working fluid gets very hot. Hotter even than the heat source (the hot heat input heat exchanger). At TDC (top dead center or full compression) the crank rounds the corner and the piston changes direction and the hot gas expands rapidly driving the piston. The displacer, 90° ahead of the piston will uncover the cold heat exchanger just as the working fluid drops in temperature due to the rapid expansion and conversation of the heat into work output. The working fluid is now colder than the supposed "sink". So, which way would the heat be flowing? The working fluid is now very cold and contracts causing a rapid drop in pressure within the engine so that now outside atmospheric pressure drives the piston inward for the compression stroke. The process repeats. The engine is not dumping any heat into the cold side. It is pulling additional heat out of it.

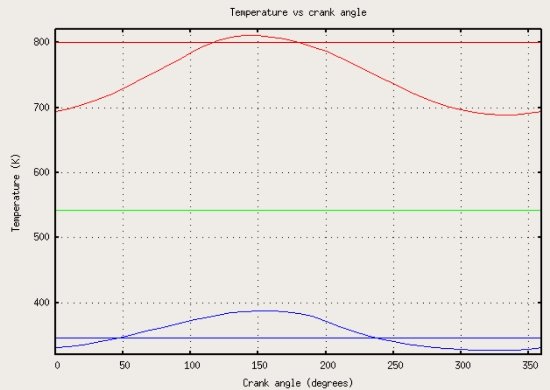
I'm skeptical of this being from a "real" engine as stated in the Wikipedia article. The "heat exchanger" lines are absolutely straight which seems unrealistic or unlikely. The image info page calls it a "simulation". Nevertheless, what I find interesting is that the working fluid on the respective hot and cold sides exceeds the temperature of the heat exchangers periodically. That is, the gas on the hot side increased above the temperature of the hot, heat input heat exchanger. And on the cold side the working fluid temperature dips below the temperature of the "sink". The hot peak is presumably full compression and the cold dip full expansion, the cooling effect being due to adiabatic expansion of the gas. Regardless if this represents real readings or just a computer generated simulation, it corresponds with my own research and findings. That is, it is what I would expect to see from real temperature readings from inside a real engine. I also don't know that taking such real time temperature readings would be possible using ordinary probes.

I'm not trying to "change the subject" I was just clarifying what I meant by "energy level". In a gas in a heat engine the collisions are basically random in all directions, there is no particular "flow" in any one direction, except perhaps as dictated by the geometry and mechanics. The effort of an engine designer should be to direct the "flow" in such a way as to impact the piston (not a heat sink). That is the tragedy of adherence to the Carnot theory. Even NASA designs their Stirling engines with active water cooling 2 inches from the heat input. indirect channeling of the expanding hot gas through a cold regenerator before it can impact the piston, heat robbing steel construction, all because Carnot thought heat had to be thrown away to a sink for an engine to complete a cycle. All this cooling and "heat rejection" is just wasting FUEL. Heat is the heat engines FUEL. Transferring it to a cold heat exchanger is like putting a big hole in your cars fuel tank. A heat engine is nothing like a water wheel where the liquid driving the engine must pass through and out the opposite side. Carnot theory is the reason there has been little advancement in Stirling heat engine design in 200 years. Maybe you could try addressing my questions to you in the second part of this post where I provided my actual understanding of the carnot efficiency limit: Is there anything there that you have any disagreement with? Starting with: "My understanding is ..." I hesitate somewhat to bring this up because I'm not entirely certain of the validity, who uploaded it, what type of Stirling engine was involved etc. But for the sake of reviewing other work and maybe not reinventing the wheel or something. Someone on the Stirling engine forum a while back pointed out a graph on Wikipedia that is supposed to be actual temperature readings of the heat exchangers as well as the hot and cold side working gas from inside a running Stirling engine. The straight blue and red lines are the hot and cold "heat exchangers". The curved lines represent the temperatures of the working fluid on the hot and cold sides of the engine. "The gas temperature fluctuations are caused by the effects of compression and expansion in the engine"

There is the assertion all over: Example: Carnot knew something else: there was an absolute zero of temperature. Therefore, he reasoned, if you cooled the fluid down to absolute zero, it would give up all its heat energy. So, the maximum possible amount of energy you can extract by cooling it from TH to TC is, what fraction is that of cooling it to absolute zero? It’s just TH−TC/TH ! I believe the equation originated with Clausius but has been attributed to Carnot. It is infact just a reiteration of Carnot's "fall of Caloric" water wheel nonsense formalized as a mathematical formula.

Not sure where the problem is. I'm thinking primarily in terms of the gas particles zipping around inside a heat engine, or outside for that matter. Some particles are "high energy", by that I mean HOT fast moving, some are low energy COLD slow moving. When a fast moving high energy particle collides with a slow low energy particle heat (kinetic energy) is transmitted from the higher energy particle to the lower energy particle. The propagation of heat can continue (or "flow") by subsequent particle collisions OK. I've already responded; I said: "Thanks, but I should apologize. My main intent in that post was to point out some of the absurd conclusions and contradictions that result from the Carnot theory generally. Like all the heat flowing to the sink at absolute zero resulting in 100% efficiency. Among other things you pointed out, that would be a violation of conservation of energy." Sorry for the confusion but you are trying to address "my thinking" in a post that was apparently a failed attempt at refuting Carnot by reductio ad absurdum.

I have no major disagreement with that ("the direction of heat flow is determined by force of numbers"). True enough, but incomplete. (Not force of numbers exclusively. Also energy level). You are also neglecting to address the fact that heat, as a form of motion or kinetic energy, may also be converted to some other form of energy entirely. At that point any "flow" of "heat" (in the form of sensible/measurable heat) comes to an abrupt end. The heat is gone having been replaced by the wheels of the engine turning and the subsequent clatter, friction and any other work output (load on the engine), electricity, if the engine turns a generator etc. The "heat" has already left AS these other forms of energy so does not need to be removed again via a heat sink. Feel free to elaborate. How do I: "persistently confuse actual machine efficiency with the Carnot limit. " A limit on efficiency is not efficiency itself, any more than a fence around a cow is a cow. My understanding is that the "Carnot limit" or efficiency equation is a limit on heat utilization, by any heat engine. Nothing more or less than that. If the Carnot efficiency be 20% then supposedly, only 20% of the heat supplied (above the ambient baseline) will be available to convert into "work" output. The other 80% of the heat supplied MUST be eliminated, "rejected" to the sink or "cold reservoir". (According to generally accepted theory ala Carnot limit) So where is the misunderstanding? Edit: The above percentages derived from the presumed temperatures in my experiment via the Carnot limit equation and would vary according to circumstance, of course. Edit: also it is understood that an upper "limit" is just that; a limit not the actual efficiency, which is generally presumed to be within that limit. The actual heat utilization being less than the (20% or whatever) calculated limit

It is a continuation of the same line of research. Previously I used insulation on engines that had metal plates for the heat exchangers on both the hot and the cold sides. Back then I had planned on using acrylic (plexiglass) on the cold side to block the supposed "flow" of "waste heat" out of the engine, but my plexiglass was brittle and kept cracking and breaking when I tried cutting it. Then that thread was locked before I could do any more, or address yours or anyone else's ideas or suggestions. Sorry. I think I may have also been banned from the forum, or just saw no point in continuing here. So the only difference is finding a means of more effectively insulating the engine. I came across these little engines with only a metal plate on the bottom, I believe intended as the "sink". The idea being to let the sun shine in through the acrylic top the heat going out the metal plate on the bottom. I could reverse that. Heat the metal plate on the bottom and "trap" the heat under the non-heat conducting acrylic dome. This, IMO should be impossible, (according to Carnot theory) the engine was not designed to run that way. But it ran just fine. To block even more heat I added the Aerogel blanket and glass dome. These additions were not included in any previous experiments. I thought the addition of all this insulating material would impress the forum members here, more than the previous use of ordinary styrofoam or house insulation. The metal cold side heat exchanger has been replaced with non-heat conducting acrylic, blanketed with silica Aerogel, covered with a glass dome. But does all that make any impression on anyone here? Apparently the invincible "caloric" is unstoppable and can pass right through anything as if there were nothing there at all. No different than the open air. Your idea or theory is as plausible as any other. Maybe the insulation on the cold side is causing an elevation in temperature on the hot, heat input side, thus maintaining a temperature difference. The temperature probes should reveal something. Sorry, my mistake I guess, but: (Screenshot attached) You quoted my statement about the engine acting as a heat pump then immediately afterward made your statement about my falling down a rabbit hole. Not sure how else to interpret that. But OK.

You say I make a good point. Thanks. But then repeat the old Carnot water wheel fallacy. Which was my point. That is a fallacy. Heat is not anything like any fluid. No energy can be derived from it's so-called "fall". Carnot's idea that "caloric (heat) has to be rejected from the cycle at the end" is no "benefit", it's utter nonsense. The water wheel "analogy" (which Carnot did not consider an analogy at all, but a literal description, literally true, that heat is a "fluid" that "falls" in temperature) implies the existence of some unknown force apart from "heat" (or caloric) itself, similar to gravity. What is the outside "force" that compels heat to "flow" between an elevated high temperature "reservoir" and a low temperature one? Water flows down hill due to an "outside" force acting on it: gravity. So water can flow into, through and out of a turbine and energy can be extracted due to gravity. There is, as far as I know, no corollary to gravity compelling heat to "flow" from hot to cold. No outside force pushing or pulling or otherwise compelling "heat" to "flow" up, down or sideways from which energy could be extracted. Heat itself is the energy. When heat is converted to "work" the heat/energy has not "fallen" due to some kind of heat-gravity to then continue along on its way to a lower level where it then "has to be rejected" . That would violate conservation of energy. "Heat" in a heat engine is just the random motion of the air particles trapped inside the engine colliding with each other, colliding with the inner walls of the heat engine chamber and colliding with the piston. When gas particles collide with the piston and the piston moves, the motion of the particles is transfered to the piston. There is no outside force, (some unknown form of heat-gravity) compelling this interaction from which energy can be extracted, is there? When the air particles transfers their motion, (energy), to the piston the motion of those particles stop or slow down. Now the air particles will not have as much energy to transfer to our temperature probe. They have been rendered "cold". No heat flowed out to any "reservoir". The "heat" of the particle does not need to be subsequently removed to a sink after this "fall" in temperature. The heat (motion/kinetic energy) has already been transfered to the piston and transformed into mechanical motion. The whole Carnot water mill idea is juvenile and should be completely discarded once and for all. There is no "benefit" in it whatsoever. Thanks, but I should apologize. My main intent in that post was to point out some of the absurd conclusions and contradictions that result from the Carnot theory generally. Like all the heat flowing to the sink at absolute zero resulting in 100% efficiency. Among other things you pointed out, that would be a violation of conservation of energy. As far as your opinion that my considering a heat engine operating similarly to a heat pump has taken me "a long way down a rabbit hole" I consider the whole Carnot theory infecting the minds of so many the actual "rabbit hole" we've been in for two centuries and need desperately to find our way out of. To reiterate, heat engines are nothing like water mills or turbines. There is no HEAT-gravity.

How is insulation different from a low temperature? According to the Carnot formula, an engine with a sink at absolute zero would be 100% efficient. At 100% efficiency, all the heat would be converted to work output so no heat would flow into or out from the sink. Likewise. Insulating the cold side of the engine mimics the condition of having the cold side at a lower temperature. Heat exchange on the cold side is reduced, the same result that would be achieved by reducing the cold side temperature. A perfect insulation would, or should have the same effect as having a sink at absolute zero. How would the engine know the difference? If there is heat flowing from the engine into a sink at absolute zero, then there is not 100% efficiency (conversion of the heat to mechanical work output). There are, IMO, unacceptable consequences to this whole Carnot limit equation nonsense. In Carnot's mind, a 100% efficient engine would be an engine that transfers 100% of the heat to the sink the complete opposite of reality. No, It is the Carnot limit equation that purportedly tells us the maximum efficiency of any heat engine with no more information than the temperature difference. Typically, in textbook examples, some actual quantity of heat in Joules is arbitrarily postulated. Example: If Carnot efficiency is 20% based on the temperature difference, and 100,000 Joules are supplied to the engine, how many Joules of heat will be transfered to the cold reservoir? 80,000 joules. Supposing 100 Joules/second as the theoretical maximum that could be delivered by the steamer, 80 Joules/second would be transfered through the engine to the cold side per second, as long as the engine is running. 20 Joules as an absolute maximum could be converted to work output. (According to the Carnot limitation). In simple terms, nearly all the heat needs to pass directly through the engine to the sink for the engine to operate. (According to the Carnot limit equation). Simply running one of these engines it can be very easily seen or felt that no such massive heat transfer to the sink takes place. The cold side of the engine remains relatively cold as long as the engine is running. Just touch it. The hot side is scalding hot. The cold side feels cool to the touch. Not very "objective", but rather convincing. It seems to me, in my experience that a Stirling engine is literally a kind of heat pump. Not a heat pump that transfered heat from the hot side to the cold side, but just the opposite. The engine is always transferring heat from the cold side and concentrating it back at the hot side, then using that concentration of heat to expand the gas and drive the piston. Contrary to Carnot's theory that a heat engine operates by "transporting" the heat between a hot and a cold "reservoir", the truth is almost the direct opposite. There would certainly be convective currents IF heat were actually being transported to the sink. Evidently, however, no such heat is transported and therefore no convective cooling is necessary. The charts from the Google image search are, of course, all over the map. It is not clear what exactly he might be referring to that related in any way to the verification of the Carnot efficiency equation, historically or otherwise. The working fluid in the model engine in the experiment, if that has not already been made clear, is just air.

It certainly does affect the result. A flow of "caloric", comparable to the flow of water through a turbine passes through unaltered. The fluid that goes in one side of a turbine comes out the other side. Heat, as a form of energy on the other hand can be converted to other forms of energy, such as mechanical motion. With "work" output, there is a corresponding reduction in heat in the working fluid.

https://galileo.phys.virginia.edu/classes/152.mf1i.spring02/CarnotEngine.htm My question is; how was it ever determined, experimentally or otherwise that this equation, admittedly based on "a complete misunderstanding of the nature of heat" happened to be "exactly correct" ? I could find absolutely no record whatsoever of any such experimental verification or even rational justification for such a conclusion. The equation itself is nothing other than the calculation of the temperature difference. A reiteration of Carnot's "fall of Caloric" nonsense in mathematical form, slightly obfuscated by being put into the form of a percentage of the absolute temperature scale. At any rate, encountering such paucity of any concrete empirical verification for this preposterous equation and conclusions derived therefrom, I decided to conduct a few simple experiments myself. So far, I do not see any evidence of the tremendous amount of "waste heat" from any of my heat engines that is supposed to be there. In fact, taking away the means of disposal of waste heat to a sink appears to have no detrimental effect on the engine. How can that be explained? Insulators are really conductors? Turbines are not actual heat engines. Turbines require some actual fluid mass to pass through them. A Stirling heat engine is sealed so no fluid of any kind passes into or through the engine. The only thing crossing through is heat or "work". Your pasting turbine performance charts from a Google image search says and proves nothing.

My question relates specifically to the carnot efficiency limit equation (rather than "cycle") though related, two different things. That equation calculates a specific ratio of heat utilization (maximum possible conversion of heat to mechanical work output by a heat engine) and waste heat rejection of the remainder to a sink. (Neglecting other factors or potential loses: friction, vibration etc.) All based exclusively on the temperature differential. To my mind, as a life long engine mechanic and repairman, this appears completely ridiculous on its face. There are dozens of factors that go into engine efficiency aside from the supposed distance of "the fall of caloric" from a high to a lower temperature "reservoir". There is an interesting article on the subject that reads: "Carnot's result was that if the maximum hot temperature reached by the gas is TH, and the coldest temperature during the cycle is TC, (degrees kelvin, or rather just kelvin, of course) the fraction of heat energy input that comes out as mechanical work , called the efficiency, is Efficiency = TH−TC/TH This was an amazing result, because it was exactly correct, despite being based on a complete misunderstanding of the nature of heat! "

I agree, but you misunderstood. I did not intend the various known facts about the experiment as an answer to your question. You said: "What you really need to do is attach thermometer probes to the engine's contact with the hot source and its contact with the cold sink, to see what the input and output temperatures experienced by the engine actually are.." I said: "That could certainly be done. I'll run the experiment again with temperature probes" That will though, of course, take some time. The infrared thermometer, I had thought would be adequate as it provides spot,as well as maximum and minimum readings, but unfortunately, as I only discovered in the course of the experiment, cannot penetrate either the pyrex? Coleman lantern glass or the acrylic. I don't think there is a need for anyone to take an adversarial stance. The suggestion is a good one. As I said, I'll repeat the experiment using temperature probes ASAP. That is not likely to be today or tomorrow. Maybe within a week.

The gas/air in the engine is heated and expands. The expanding air drives the piston outward doing work. A certain percentage of the heat, (a form of molecular kinetic energy of the air molecules) is transfered to put the piston in motion, (a different form of mass kinetic energy). As a result the air loses energy. The loss of energy results in a reduction in temperature (of the gas/working fluid). A reduction in temperature of the gas is necessary in order for the piston to return (recompressing the heated and expanded gas) If the gas is not cooled back down in some way, the air cannot be re-compressed and the cycle would end there, the engine coming to a halt, unable to fully recompress the heated and expanded air. Carnot efficiency is the ratio (percentages) of working fluid cooled by the above described conversion to work output and the remaining heat which needs to be gotten rid of by conductive transfer to the sink. If 10% of the kinetic energy is transfered to the piston, the other 90% must be gotten rid of by transfer to the sink. So to complete a cycle, if the engine is 20% efficient at transferring energy to the piston, the other 80% must be wasted or "rejected" through the engine to the sink or cold side. So the work the engine does IS what you get from the 20% or whatever efficiency. No? That is my understanding anyway. The remaining unconverted "waste heat" must be transfered to the sink so that the working gas (air) can cool back down and contract. Otherwise the piston has to expend as much energy to compress the gas as it received by the gas while it was being heated and expanded. The efficiency is supposed to be a measure of the work output of the engine. Whatever heat does not go towards driving the piston out has to be gotten rid of. So there is a "minimum percentage of heat rejection required for the engine to complete a single revolution." If the engine is 20% efficient at converting heat to mechanical "work" the remaining 80% of the heat would be that percentage of heat "rejected" to the sink. I don't see how that follows. If I have a heating element in a box (like an oven) and there is no insulation, the walls of the oven exposed to outside air, the walls will be relatively cool. Insulate the outside of the oven and everything inside would heat up to a uniform temperature eventually. I can see your point to a degree, but I believe convective cooling is a huge factor. Otherwise what use would any insulation be anywhere? Why do people insulated their homes, attics, wear coats, use blankets etc. except to reduce convective cooling. On what basis do you draw the conclusion that engines of this type do not approach "the carnot limit"? In what way is that anything more than your personal opinion? How could this "Carnot limit" ever be tested objectively by actual experiment? As far as I've been able to determine it (the Carnot limit) is nothing more than an unverified supposition. Where and when and how has it ever been empirically demonstrated? I can find no historical record of any such thing, only that Sadi Carnot thought heat was like water "falling" from a high to a low temperature so considered that the "distance" of this "fall" somehow determined efficiency. He, BTW abandoned that hypothesis when it was discovered that heat is a kind of motion rather than a fluid, and recommended others abandon it as well, but died before these views were ever published.

The particular engine used in this experiment is available from eBay or Walmart. https://www.ebay.com/itm/254879289942 The type of engine does not seem to be particularly relevant though. I've done many similar experiments using various types and brands of Stirling heat engines with similar results. This one however is a "gamma" type "low temperature difference" engine with a magnetically actuated displacer. Carnot efficiency is what's at issue. Carnot efficiency is a percentage. The heat source (facial steamer "sauna") is rated 100 watts, if that's of any help. According to online sources that would be 100 joules per second, assuming all of the that wattage actually went into the engine which is obviously not the case. Enough steam was escaping to fog up the glass going around rather than into the engine. Logically though, I would think that if the temperature difference is 88K and more than 80% of the heat applied passes through to the sink but has nowhere to go, the cold heat exchanger should quickly heat up to nearly the same temperature as the hot side heat exchanger. The engine displacer is constantly transferring the working gas (air) from the hot to the cold side and back. There is no regenerator. The cold side should quickly heat up, excluding conversion of the heat to "work" output that is.

OK, I'll do my best to supply the additional information requested ASAP. Thanks! 212°F = 373.15 K 71°F = 294.81 K Therefore Carnot efficiency = 20.994% Heat rejection should then be no less than 79.006% At least that is how the heat rejection is typically calculated in textbook examples.

Thanks. There is a rather complete and thorough text description before the video. If not adequate I'd be happy to post any additional information requested if anything isn't clear. I'm not relying on video but I assume video is not forbidden as a supplement to a description, is it?

It is my understanding that the less heat that is used by the engine the greater would be the amount of heat that would need to be rejected to the cold side so as to cool the engine each cycle so the piston could complete a cycle. In other words 2% used, 98% rejected = 100% or 20% used 80% rejected to the sink. So the less efficient the engine is at utilizing the heat, the more heat rejected, the faster the cold side should heat up. Is that incorrect? Also the bottom of the engine body or hot side is aluminum. The rest of the engine body or cold side is acrylic. Aluminum is an excellent heat conductor. Acrylic is a very poor heat conductor. Even without the added insulation it is difficult to understand how acrylic could serve very well as a heat sink. That could certainly be done. I'll run the experiment again with temperature probes However, logic would seem to dictate that the hot bottom would be near 212°F and the top cold side no less than the room temperature which was about 71°F give or take a few degrees. That is enough information for an estimate of the maximum Carnot efficiency and minimum percentage of heat rejection required for the engine to complete a single revolution. The engine ran a total of 3 hours before I concluded the trial with no indication of slowing down. (After I stopped the insulation from rubbing on the flywheel too much, that is) BTW, I'm not suggesting that the engine could run without a temperature difference, necessarily. It seems certain, if the engine is running there is a temperature difference. The question is, how is the temperature difference maintained? There are two means of reducing the temperature of the cold side, or maintaining the relatively cold temperature of the cold side. 1) heat rejection 2) heat conversion to mechanical motion, vibration, sound, or thermodynamic "work". I would suggest that if #1 could be largely eliminated then it could be assumed that #2, heat conversion to other forms of energy would be the primary source of cooling.

I've done nearly everything possible I can think of to block the "flow" of heat out of a Stirling engine, with the idea that if the "heat rejection" could be blocked, the engine would quickly overheat and stop running, or be unable to start running in the first place. To that end, I recently sent away for a silica Aerogel blanket, which is supposed to be very good at blocking heat. I was able to apply a propane torch to one side and not feel heat through the blanket with my hand on the other side. I also used a glass globe from a Coleman lantern to block drafts. As in previous experiments just using styrofoam or house insulation, the engine started and continued running. This result seems contrary to the "efficiency formula" or "Carnot limit" which, would calculate that some 80% or more of the heat supplied to or entering into the engine would need to be rejected to the sink or cold side back to atmosphere for the engine to continue operating. So why does the engine not stop from overheating when the cold side is insulated, blocking the flow of heat out of the engine to the "cold reservoir" ?

Yes, I thought so, as I mentioned, something didn't look right. The result of a hasty cut n paste on the Stirling engine forum, which I then repeated here. Which "It". Sorry, I copied the wrong equation to start with. The Carnot efficiency is what I meant to address. At any rate, that a theory is more or less consistent with itself is no empirical validation. Please site an example. I've heart this affirmation repeated over and over and over, but that seems to be all it is. I've scoured through the available literature for ten years and find no accounts whatsoever of any detailed experiment demonstrating, for example, the actual heat flow in and out of a Stirling engine, running a Stirling heat engine on ice, insulating the sink, nothing whatsoever that would either add weight to or call into question Carnot's conclusions. What I have found is that in Carnot's own journals, not published until many years after his death, he expressed grave doubt about his own theorem. Stating: to paraphrase, as I don't have it in front of me: If heat is Kinetic energy, it is difficult to understand why a cold sink should be necessary. Of course, it can be assumed there have been limitless experiments over a centuries time, but infact, Carnot himself conducted none, as far as I'm aware. In his book he confessed he did not have access to so much as a Steam engine, as they had not yet been introduced in France. His thoughts were just that. Mostly philosophical, not empirical. From then on the "observation" has been almost 100% exclusively: hundreds have made the attempt to construct a "self acting engine" but none have succeeded, it can be concluded therefore that it is impossible. End of story. Please give me one example of "detailed empirical observation" by ANYONE, gifted or not, specific to this order of Stirling type heat engine, or any other for that matter of the "external combustion" class. Hardly anyone in history ever really fully comprehended how these engines worked, no less built any for experimental analysis. They were superceded by the internal combustion engine and electric motors and forgotten for the most part for 100 years, until recently. I'd LOVE to have the opportunity to read such a detailed empirical, experimental analysis. Finding NON WHATSOEVER myself, after a long and diligent search, I concluded I was obliged to fork out the cash to buy half a dozen such engines and/or build and/or modify my own, and run some tests. As far as I was able to find, nobody ever really bothered, everybody just assumed that others already have. Please, please, please fill me in, so I can be saved the expense and effort involved in reinventing the wheel, or going over old ground already covered. One example of anyone ever insulating the sink for example to measure how cold it might get if thermally isolated from the outside environment. Nobody ever tried it because it seems completely ludicrous and goes completely against accepted ideas about how these engines operate. It is just assumed that some 75 to 80% or more of the heat in a heat engine running at 20-25% Carnot efficiency is being dumped into the sink, and the engine couldn't run otherwise. Apparently that's a complete fallacy.

I don't see what is so contradictory about saying I understand a point of view, I just don't completely share that point of view. Given my way of looking at things and my experiences in life, I see things differently. I'm willing to discuss it, and I will try very hard to understand why someone else thinks the way they do, or sees things differently, and I'm more than willing to be convinced, if the argument or explanation they present makes sense. But when people just take on an air of authority and expect me to accept whatever they say without question, I'm not impressed. For example, the only logical solution I have been able to come up with for the formula for the Carnot efficiency of a heat engine, why it calculates nothing but the temperature difference is that it is a holdover from Carnot's own theory of heat. It's the maximum "height of the fall" that the "caloric" can travel, from the hot reservoir to the cold reservoir. It is known that the entire premise on which this mathematical formula is based is completely erroneous and not representative of reality, yet it is still taught and used and spoken of as if it is absolute, unshakable, unquestionable physical law. Yet, when I examine it closely, it makes no sense whatsoever. It doesn't even add up. At this point in time it embodies two incompatible completely irreconcilable pictures of reality. If my heat engine is 500 degrees on one side and 250 degrees on the other than the "caloric" can only fall 250 degrees from 500 down to 250 which is 50% of the "fall" on the way down to absolute zero. (Arbitrary numbers on the Kelvin scale but it works out the same way on any other) That makes my engine 50% efficient, at best, because that is as far as the "caloric" can possibly fall. It is a hard limit for the same reason that sea level is a hard limit. The liquid can't flow any lower than the lower reservoir. If we know heat is not a fluid, but energy that can be converted, then why continue to use a formula derived from a misconception about the very nature of heat. So I'm told that the original theory was wrong and nobody believes it anymore, but "somehow Carnot managed to get the math right", though he had no concept of absolute zero at the time. The whole thing is a hodge lodge of irreconcilable theories munged together by a completely simplistic formula that takes into consideration nothing whatsoever that has any actual influence or bearing on any engine efficiency. I understand how it works, or is supposed to work, I think. But I can't for the life of me understand how people can actually believe it. It has no foundation or basis whatsoever in reality. It's nonsense. Why should anyone give it a second thought? It doesn't even work out in practice in a way that makes any sense, because if an engine actually IS 100% efficient, "carnot efficiency" might be 15% or 20% If my heat engine utilizes ALL the heat fed into it, and converts every bit of it into useful work so no heat whatsoever "flows out" into the sink, carnot efficiency might be calculated at almost any arbitrary number represented by the temperature difference. How efficient the engine actually is doesn't enter into the calculation at all. It's complete hogwash.

Methylene chloride is what's inside the drinking bird, everybody probably already knows that though. If someone wants to run a heat engine on evaporative cooling though, I think it's more practical to use a Stirling engine. There are a number of ways I think this one could be improved. Not my engine or my video BTW. The guy that built this engine died several years ago. This engine is running on only a 2.5 °C temperature gradient. Not many have succeeded in building a model heat engine this sensitive. I can see there is a vent hole, which is usually needed in a diaphragm engine because it is completely sealed (no leaks around a piston), used to equalize pressure if needed. Like when the barometer falls. But I suspect, though I have no proof or any real reason to think so, that it may have been used to fill the chamber with helium.