TonyMcC

Michelson and Morley in 1887 tried to prove that the speed of light was not a constant and failed. It was soon seen that the reason their experiment had failed was because the speed of light is a constant (which surprised them). http://en.wikipedia.org/wiki/Michelson%E2%80%93Morley_experiment By the way any radar equipment works by determinig the time taken for EM waves to travel a given distance.

It is usual for competition class rifle competitors to lower their heart rate as they gently squeeze the trigger. This and breath control helps keep the rifle steady.

" A conjecture is a proposition that is unproven but appears correct and has not been disproven". The first part of what I wrote is the conjecture and the second part attempts to show that if the cojecture is proved then a proof of Fermat's Last Theorem would be easily found. Although written in Latin a translation of Fermat's writing is "It is impossible for a cube to be the sum of two cubes, a fourth power to be the sum of two fourth powers, or in general for any number that is a power greater than the second to be the sum of two like powers". Irrationality is not mentioned! What little I have read and understood of elliptic curves, modular arithmetic and the Tamiyama-Shimura Conjecture seems to concern itself with patterns of numbers. Again, although there is much I haven't read, irrationality seems to get no or little mention so it seems to be a fair assumption that the patterns concern themselves with rational numbers. Andrews Wiles, as far as I know, never said his aim was to prove irrationality and at the end never stated that was what he had proved or that irrationality was an outcome of his proof. You mention D H. Perhaps you should read posts 13, 15 and 16. Anyway, I sggest the addition of claiming that irrationality occurs in all relevant equations is enough of a change to warrant a new conjecture. I think a new conjecture can be claimed even though a proof that may not involve irrationality has been accepted. As the first part of what I wrote is a conjecture it cannot be said that the second part is a proof - just evidence that if the conjecture is correct what could then be proved as a consequence.

Make it your intention to run twice the distance (say 200 metres) and then change your mind when you are half way there!

You are considering ideas associated with analogue computers. Have a look at http://en.wikipedia.org/wiki/Analog_computer

I personally don't think I am saying anything startling or particularly new. I certainly can't prove the reqired irrationality. However Fermat didn't specifically mention irrationalty. I believe in Fermat's time many mathematicians in the Western World were sceptical of the idea. I haven't seen anyone else try to analyse incorrect sums using geometry and use the idea of similar triangles the way I have. I have found a certain reluctance occurs as soon as irrationality is mentioned and a better mathematician than me seems to doubt that proving irrationality would lead to a simple solution. I think you understand what I have posted. Whether the irrationallity of the Golden ratio can be somehow be used is something I just don't know. Apparently the term "Golden Ratio" was first used in the 1800's. Hi Slick, I can't really see what you are getting at. However I see you are making isosceles triangles . The base of an isosceles triangle is 2*(the square root of something). Is zero twice the square root of "something". A long time ago I decided an extremely important property of any number is that it is "the square root of something". I find the following quite satisfying - If I superimpose the curves in my diagram onto your diagram I can see that your large triangle roughly fits my cube root curve. Not only that, but the ratios are ( roughly) 0.8, 0.88, 1.0. Allowing for approximations due to playing with a ruler on my laptop face I deduce 80^3 + 88^3 = 100^3 and 800^3 + 880^3 = 1000^3 etc. etc. This illustrates my use of similar triangles.

DH - Thank you for pointing out Euclid's construction, I wasn't aware of it and so that can be my "learn a little every day" for today. I have amended my simple thoughts thread. Also I an not familiar with the Dedekind cut. I will read up on it soon, but at first glance it just seems to say that there is a gap between a set above "+0" and a set below "-0". I assume that any number in the gap will be irrational. If I have this completely wrong please don't concern yourself - I shall have an interesting time studying it. I can also understand "the wrong order" comment. Because I set out from the beginning to use a novel approach (analyse incorrect sums) geometry seemed to be a way to do that. Having said all that I note you have not commented on whether, in your opinion, my conjecture is valid. I will add a little clarification to it, Tony McC's conjecture:- In every correct sum a^n +b^n = c^n, if n is a whole number >2 and a, b and c are positive numbers >0 then one or more of the terms a, b or c is irrational. A consequence of this is that if a triangle is constructed using a, b and c at least one side will be irrational. Because of the irrationality no similar triangle can be constructed with all three sides integers. Therefore there is no integer solution to the equation x(a^n) + x(b^n) = x(c^n) where x is any number. This proves Fermat's Last Theorem. In summary if the irrationallity mentioned above can be proved then Fermat's Last Theorem would be easily solved. Please comment.

Thank you D H . I need to revise my conjecture. I had not meant (I think obviously) to exclude part of the equation by the use of zero. So here goes :- Tony McC's conjecture (Revised) (a) In all equations of the form a^n + b^n = c^n (where a, b and c are positive numbers >0 and n is a whole number >2) one or more of the terms a, b or c is/are irrational. (b) A consequence of (a) above is that it is impossible to form an equation of the form a^n + b^n = c^n, where a, b and c are whole numbers >0 and n is a whole number >2. You seem to accept that part (a) is true (essentially a restatement of Fermat's Last Theorem). You also seem to believe irrationality exists in all relevant examples ( post 13). Have you a proof of this? Do you think part (b) above follows? I'm still in front of the firing squad, but not shaking quite as much!!

Hi tree, Sorry if I misinterpreted some of your responses in post 11. When I suggested that there no NON integer values I was trying to suggest one of the terms a, b, c was infinitely long when expressed in decimal form and could not be simplified. i.e. I was suggesting irrationality. Your response that it quite easy to find examples I took to mean you could find examples which were not irrational. You seem to suggest that the infinitely long term could be of the form x=a/b. That is why I challenged you to provide an example of a^n +b^n = (c/d)^n. (usual provisos) You have not commented on my reasoning using similar triangles so I assume that is sound? As I say, sorry for any misunderstanding. Incidentally I first floated the idea of irrationality in "Fermat's Last Theorem - simple ideas" on 18th March. D H says it is the height of hubris to think an amateur could solve Fermat's Last Theorem. I have to agree with him, but if people find it an interesting problem to chew on and exchage views with like minded people then what is the harm? It should not be forgotten that if Fermat did indeed have a proof it would have had nothing to do with Wiles' proof. I think I'll demonstrate a little hubris myself:- TonyMcC's conjecture:- a) In all equations of the form a^n + b^n = c^n (where n is a positive whole number >2) one or more of the terms a, b, or c is irrational. b)This results in the impossibility of forming an equation of the form a^n +b^n = c^n where a, b, and c are positive whole numbers and n is a positive whole number >2. I stand before the firing squad!!!

I was assuming a, c and n were positive integers. I don't think there is a whole number solution.

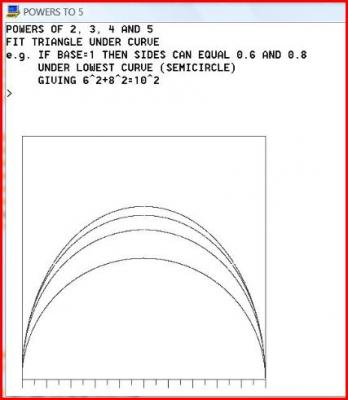
Slick - firstly let me say I am no mathematician. However just as you can use a semi-circle to find a, b, and c in the equation a^2 + b^2 = c^2 you can use an appropriate curve to find a, b, and c in the formula a^n + b^n = c^n. I attach curves for n = 2 to 5. Interestingly, if I had drawn curves for n=2 to n=infinity they would fill the shaded area in your diagram. It is accepted that many square roots are irrational. It seems to me that we can expect that often a, b, or c will be irrational in the general formula a^n + b^n = c^n. However, it seems to me that Fermat may have proved (or thought he had proved) that ALWAYS at least one of the three terms a, b, or c will be irrational if n is a whole number >2. As you can read above, "D H" seems to think that is the case and "the tree" seems to think that it may not be the case. In other words the idea is cotentious. I agree that a^n +1 = c^n cannot have an integer solution. Sorry about repeated text - I cocked up attaching the diagram.

I wonder if you move forward or backward in time the earth will not be where it was when you left. You might find yourself in the emptiness of space!

Hi tree (no pun intended!), Thinking about your first point, I think the following thought experiment (or fairy story) is in agreement with Fermat's comments (whether he could prove it or not is another matter):- You have two cubic containers of liquid and wish to fit them exactly into a single cubic container. You come across an elf who specialises in making cubic containers. In fact he has spent eternity making such containers and in his yard he has in infinite number, each of different size (He also has an infinite sized yard of course!). You and the elf agree that there must be a container in his yard that is the correct size. He starts to find the required container by trial and error. If he selects one that is too large then he tries a smaller one and vice-versa. After spending more time than you will ever have (for you will have ceased to exist eons ago) he finds he has two containers one is too large and one is too small although the size difference is infinitely small! The elf mutters to himself "This doesn't seem to make sense!" I would very much like to see an example of a^n + b^n = (c/d)^n where a, b, c and d are whole numbers.

Well, as I see it, if you tell me that c is irrational and a and b are rational in a^n + b^n = c^n (n>2) then it follows that c is a number followed by an infinite number of digits after the decimal point. Either that or we are dealing with infinite numbers! You can imagine drawing a triangle using the values of a, b and c but you would have to multiply all sides of the triangle by an infinite amount to achieve a whole number similar triangle. You can prove with geometry that if a^2 + b^2 = c^2 then c(a^2) + c(b^2) = C^3. (Which won't come as a surprise!), but doing this provides enough data to produce a different triangle appropriate to a^3 + b^3 = c^3. In fact this is the way I drew my curves in" Fermats Last Theorem - simple ideas, post 23".

D H - That is exactly why I had to use an approximation. If what you say can be proved then surely Fermat's claim is justified when looked at in the way I describe?

Firstly - Happy New Year! the tree - I would like to concentrate on your last comment as mathematics is not my strong point. However I can't see a flaw in my mathematical reasoning and would appreciate any required correction. 6^3 + 8^3 = 728 = 8.995883^3 ( Approx of necessity!) An acute angled triangle of sides 6, 8, 8.995883 could be drawn to represent the equation (same idea as right angled triangle) If all sides are multiplied by the number of digits following the longest number of digits after any decimal point we can make a similar triangle of sides 6000000, 8000000, 8995883 (i.e. whole numbers) Because of this similarity we can say :- 6000000^3 + 8000000^3 = 8995883^3 (Approx of necessity) 7.28E20 = 7.2800002E20 (difference due to approximation) This is an example of what I posted in "Fermats Last Theorem - simple ideas entry 23" It seems to me that if you can present me with an equation using finite numbers following all three decimal points I could easily give you a whole number solution. I would like to consider your other points further before replying - thank you for your interest.

It is quite possible although usually looked at the other way. The transmitter transmits and the receiver is tuned to the transmitter. Examples are radio and television systems. In these systems the transmitter sends out EM waves at a particular frequency and only those receivers which are in range and have their input circuits tuned to that particular frequency will receive transmitted energy. Quite recently devices been made to pick up radiation at 50 or 60 Hz which is used to (say) charge a mobile phone in the home. This is usually described as magnetic induction see http://en.wikipedia.org/wiki/Battery_charger and scroll down to "inductive".

Not very often, but occasionally when an aircraft hits turbulence and drops suddenly people get hurt, sometimes breaking bones. If a reliable airborne detector of air turbulence is perfected I would be surprised if the Civil Aviation Authority (CAA) did not insist that passenger carrying aircraft be equipped with it. On a lighter note :- A little old lady asked at the check in desk "Do your aircraft crash often?". She received the reply "No Madam, only once".

Surely when you see your ball of sticky stuff "disappear" it still exists as a very long very thin track on the earth ? Perhaps I don't understand the question.

I wonder if Fermat was implying that there is no NON integer values for a, b and c for the equation a^n+b^n=c^n. The reason I say this is that if you could obtain complete values in decimal form you could get a whole number equation by multiplication. For eample let us say that 6^3 + 8^3 = 8.995883^3. If this was true then we could say 6000000^3 + 8000000^3 =8995883^3. I think Fermat found (or thought he had found) that at least one of the values for a,b or c had to be infinitely long and this is the reason whole number values could not be obtained.

From what I read ground based radars are not very good at detecting clear air turbulence (CAT) at long range. With development this may improve. However if an aircraft can be given a system that reliably detects CAT at relatively short range it would be an additional safety device that would save lives. When you consider the cost of buying and maintaining a Jumbo Jet the cost of one more safety device would (in my opinion) be negligible.

Aircraft flying into turbulence is a serious problem. There is ongoing research into detecting it using radar and, I believe most recently, optical systems. If interested some information about optical systems can be found http://www.ophir.com/turbulence_detection.html I can't see sonar being useful because (as alpha2cen says) the speed of sound waves through air is too slow. In fact slower than some military aircraft!

What is needed is for someone to tell us he has died in a dream! That's not me: is it you?

Yes - that's how I read the question - there is a bit more to do to finish the question.

Jackson33 - Thank you for your kind thoughts and comments. However I am very content with my life and not seeking improvement. I tried to highlight the fact that today, although I and my wife have the sort of problems associated with old age, we are well cared for by the "system". My father was in fact well cared for by the "system" current in his time - 6 months in hospital and treated with penicillin - but what was available in knowledge, techniques etc. were not of today's standards (nor could be expected to be). I realise that all the medical care we receive has to be financed and in that sense is not really free. However during my working life I paid quite a lot of tax and even now I pay income tax etc. out of my pension. I suppose I was using my own life experiences to illustrate the fact that there has been a vast improvement in the lives of ordinary people over my lifetime (and yours).