TonyMcC

Perhaps I'm missing something - but the words extraction and urine still come to mind!

I'm not sure you your sense of humour is universal !

You had to do some work to get it moving. Momentum will keep it moving. Some work is needed to slow it down or bring it to rest. In practice work is needed to maintain velocity due to resistance caused by friction etc..

If you are able to seriously consider this scenario as existing due to lack of food then logically you might as well consider the killed people as a source of food!!!

If you think it possible that one of your programmes is causing trouble at startup then you can run a Windows utility called MSCONFIG. I think you can do this after starting in safe mode. It will allow you to selectively remove programmes at startup completely safely (You just untick boxes that can be reticked later). The proceedure is slightly different for different Windows versions but info can be gained via Google. In vista you type in MSCONFIG and select Run. Then select the Startup tab and I suggest you untick all boxes to see if your computer restarts properly. If it does try selecting programs by ticking appropriate boxes and restarting.

The work done in deformation creates heat in the object(s) that deformed.

When a skydiver leaves the airplane he is pulled toward the earth by gravity. However his speed will soon stabilise at about 120 mph. Do you think that this has a bearing on your second answer?

Reference question 3, Why not throw a ball into the air and observe what happens?

I don't know about this video, but it is possible to make a wind driven device that can move faster than the wind pushing it. A sports sailing dinghy can do this when travelling across the wind. This is basically because the sail act as an airofoil generating horizontal "lift" in the direction of travel. travelling down wind with the wind behind you can be a much slower process.

Does anyone dispute these statements:- i) You can take two squares of the same thickness made from some malleable material and measure the sides (X and Y). You can mix the two together and form a single square of the same thickness and measure its side (Z). The sides will ALWAYS give you an equation X^2+Y^2=Z^2. So there is ALWAYS a solution. ii) The only way to prove this mathematically is by means of geometry. iii) This is because most solutions contain at least one irrational term. iv) The only way to discover the relatively few whole number solutions is by some form of "trial and error".

. It seems to me that you can think of sums such as 3+4=5 and 5+12=13 as incorrect sums that can be corrected by squaring each term. It also occured to me that "Fermat" is saying that any such sum for any power above 2 must include at least one irrational term. I wondered how incorrect sums could be analysed and decided that all relevant incorrect sums could be formed into triangles. e.g. since 6^3+8^3 approximately equals 9^3 then a triangle of sides 6,8 and approximately 9 can represent the relevant incorrect sum. If you form enough of the triangles for a particular power you can produce a curve that can be used in the same way that a semi-circle can be used for power of 2. To make the curve universal ( e.g. for power of 3) let the base be 1 and the other two sides be the cube roots of the two fractions that add to produce 1. As an example cosider the correct sum 0.25+0.75=1 then the required triangle would have sides of approximately 0.63,0.91 and 1. Thus 0.63^3+0.91^3=(approx)1, hence 63^3+91^3=(approx)100^3. Well,my illustration shows curves for powers 0f 2,3,4 and 5 and examining the curves doesn't help much! It took me some time to realise that there is a big clue in the maths I employed to draw the curves (I wrote a short computer program). This realisation slowly formed in my mind as I considered practical uses for triangles. I feel I can provide strong evidence that the assertion made in Fermat's Last Theorem is true. Proof? - well that may too much to hope for, or perhaps not! I have read a few books on the subject, but I am not aware of anyone else taking this approach. Anyone out there worked along similar lines ? Does my approach seem reasonable?

Onefrom the UK. Not my car!

Talking to myself here lol. You could set VA to a 6V sine wave and VB to an 8V sine wave. Having done so you could alter VC to any value between 14V and 2V (including, for example, cube root of VA^3+VB^3) in at least two seperate ways. a) Have a variable phase shift and set it to somewhere between 0 degrees and 180 degrees. Alternatively:- B) Have a variable gain summing amplifier and set it to a value of less than 1. This is another example of a "machine" that can provide you with the nth root of A^n+B^n BUT it demands 3 variable inputs!

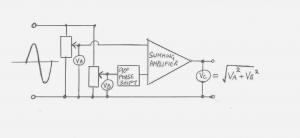
In the early days of computer development the analogue computer had its following. One of ts attributes was the ability to handle irrational numbers both for input and output. The circuit shown is a simple analogue device which will accept two inputs (VA and VB) and produce an output (VC) which is SQR(VA^2+VB^2). i.e. If VA=3 and VB=4 then VC=5 If VA=1 and VB=1 then VC= SQR(2) If VA= X^n and VB= Y^n then VC= SQR(((X^n)^2)+((Y^n)^2)). Or VC= SQR(X^2n + Y^2n) What simple change to this circuit could be made to make the output (VC) equal to the nth root of VA^n+VB^n ? e.g. set VA=6, VB=8 and ensure VC= Cube root (6^3+8^3) instead of 10 ? What are the implications for Fermat's Last Theorem? Will soon get on to triangles!

The following describes a unique property of a sine wave:- Take two sine waves of any amplitude but of the same frequency (i.e same periodic time or using the same distance for 360 degrees on the X axis of a graph). Draw a graph of each, one above the other. Slide one waveform along the X axis (i.e give it phase shift). Working point by point vertically add one graph to the other to form a composite waveform which is the addition of the two above. You will always find the resultant composite waveform is also a sine wave. By definition each point on a sine wave is the square root of something (SQR(A^2+B^2)). Thus each vertical calculation made to form the composite waveform is a correct sum of the form SQR(something)+SQR(something)=SQR(something. (Very often 1, 2 or 3 of the "somethings" may well be irrational). Now, if you take 3 points, one from each of your graphs, not vertically in line, you will make an incorrect sum also of the form SQR(something)+SQR(something)=SQR(something). Since sine waves are curves you will ALWAYS be able to find an incorrect sum that can be corrected by squaring each term. (As before 1,2, or 3 of the terms may well be irrational). Where do we go from here? Think triangle!

Thank you timo. That is exactly what I meant by "cut across". Out of interest I will mention that the devices that I am familiar with deliberately use magnetic fields at right angles to the direction of moving electrons for maximum effect. Examples include cathode ray tubes and cavity magnetrons.

An easier water analogy to understand is to consider a closed water circuit such as a pump pushing water through (say) radiators. The pump provides pressure to force the water around the circuit and in many ways is similar to a battery forcing electrons around an electrical circuit. The pipework and taps on the radiators offer opposition to the water flow and can be likened to resistors in an electrical circuit. If you completely close a tap you will stop the flow of water. In an electrical circuit you do the same by providing an extemely high resistance. This happens if you break the electrical circuit. Note this does not stop the pump producing pressure nor the battery producing voltage.

To alter the path of a beam of electrons (and presumably ions) the electrons have to cut across the magnetic lines of flux, not along them.

In the book "The Hitch Hikers Guide to the galaxy" by Douglas Adams a super computer, after millions of years of deep thought, answered a question. The question was "What is the answer to the Ultimate Question of Life, the Universe and Everything". The anwer given was 42. I'm afraid the computer got it wrong - the correct answer is "The Sine Wave" . I am quite serious, after all you can't get far in mathematics, physics or any branch of engineering without it appearing in your calculations. I have given this some thought (a bit less time than millions of years!) and will float those thoughts later.

Hope you had a happy birthday DivaGreen. I shall resist the urge to say perhaps I shall look forward to placing myself in your hands! Best of luck with your further studies.

Absolutely agreed. However the poster of this thread specifically mentioned positive ions. Although not that important, I thought I would just correct your statement that crt televisions produce the display by pushing ions about with magnetic fields. They do, as I'm sure you know, actually push a beam of electrons about with magnetic fields. I'm probably just nit picking, if so I apologise.

Since an ion has an electric charge it will experience a sideways force if moving across lines of magnetic flux. One small detail - in a cathode ray tube the cathode emits electrons and it is moving electrons that are deflected by a magnetic field. If you are considering positive ions I would expect them to be deflected in the opposite direction to electrons. Also since an ion has a larger mass:charge ratio than an electron I would expect any deflection to be less for any given speed and magnetic field strength.

I am 72. I used to talk in other peoples sleep. Only half of what I said was true but I didn't know which half. In other words I used to be a college lecturer.

Here's another simple thought. Fermat seems to imply that the nth root of A^n + B^n is irrational. Have you ever wondered how far you could get without using numbers at all? Let's consider the case of two cubes. I give you two cubes which I have measured at 3 cubed and 4 cubed, but instruct you not to measure them except to determine if there is a whole number ratio. In other words you wouldn't know whether they had sides of 3 and 4 or perhaps 6 and 8. Since there is a whole number ratio you could slice the cubes into equal thickness slices. You would then have 3 solid pieces 3*3*1 and 4 solid pieces 4*4*1. Using only a right angle you could form the 3 solid pieces into a single solid piece which would be sqr(27)*sqr(27)*1 and the 4 solid pieces into a single solid piece which would be sqr(64)*sqr(64)*1. Similarly using only a right angle you could form a single solid shape which would be sqr(91)*sqr(91)*1. So you could transform any 2 cubes into a solid which has a square face and a depth which is smaller than the side of the square and this can be done without using numbers at all. It would seem that we are half way there! BUT if I give you a solid shape which has a square face and a depth less than the side of the square, what manipulations are needed to reshape it so that it becomes a cube? Just thinking!!