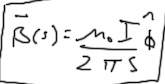ambros

Ok, I moderated myself and deleted provocations. There is nothing to integrate really, this is the formula, that's it. There is this one and there is the other one you wrote down - but one of them is wrong or simply does not apply to these same situations. I've given many different Wikipedia articles that all confirm what equation is correct and more appropriate. Does no one have some instruments handy to measure this and resolve the problem? Alternatively, I'll find some experimental data in some paper or somewhere. http://dev.physicslab.org/Document.aspx?doctype=3&filename=Magnetism_BiotSavartLaw.xml - "The Biot-Savart Law is much, much, much more accurate than Ampere's Law (as its applications involve fewer assumptions)." -- We should really talk how that equation can come from Maxwell's equations, I did not think I would debating Biot-Savart law as it is well documented, and I am even very well aware how that alternative equation came to be: This is wrong, I do not know what is this, it' crazy. DISTANCE to that segment dl is not the same R that is in the equation, but the real distance is 'r' in that scenario. They are thinking to be measuring "dl" at distance R, but they are actually measuring it at distance r. What will their instrument measure? It would measure the CLOSEST segment to that 'point'. In order to measure segment dl at distance R, then they surely need to move the instrument right next to dl, so the distance R points to the middle of the segment dl, and so that R is indeed the shortest path and real "distance" from that point to that segment.

It is not only ridiculous but I believe it is even against forum rules to keep making wrong statement and false assertion while blatantly and repeatedly refusing to provide any REFERENCE. Have you derived these from Maxwell's equations and will you provide some reference finally? Merged post follows: Consecutive posts merged FOR STRAIGHT WIRE(s) WITH STEADY CURRENT: YOU SAY THIS IS CORRECT: I SAY THIS IS CORRECT: - "The physical origin of this force is that each wire generates a magnetic field (according to the Biot-Savart law), and the other wire experiences a Lorentz force as a consequence." Ampere's force law is unsuitable approximation, Ampere's circuital law is unsuitable approximation too, and that's why the first paragraph in that Wikipedia article is clear that this interaction is actually DEFINED by BIOT-SAVART LAW and LORENTZ FORCE, and not with any of Ampere's and Maxwell's equations. Why? Because they are *different*, and it should be obvious by now what equations are more *accurate*, PICK ONE! -- I will not discuss basic vector calculus with you, check some real world measurements.

Ay, caramba! There are two forces there and they act on TWO DIFFERENT objects. The "net force", of course, is the one that will correctly calculate the relative displacement, and both of these two forces play part there, as illustrated, of course. Do you not understand "distance ®" is the SHORTEST PATH? Do you not see what is 'angle', what is 'dl' and what is 'r'? Now, compare that with your source - it's not the same, and if it was then "your" result would be wrong. Your source does not talk about any case scenario I have given here, what it talks about is simply insane. Why don't you trust my source? http://en.wikipedia.org/wiki/Biot%E2%80%93Savart_law http://en.wikipedia.org/wiki/Magnetic_field http://en.wikipedia.org/wiki/Amp%C3%A8re%27s_force_law What part do you think states you are correct? Maybe this: - "The physical origin of this force is that each wire generates a magnetic field (according to the Biot-Savart law), and the other wire experiences a Lorentz force as a consequence."? Ha-ha. ...and your equations, that's just hideous. How did that happen? Because you did not PROVIDE ANY REFERENCE, and I'm talking about these four monsters that you supposedly DERIVED FROM MAXWELL'S EQUATIONS:

Le Bureau international des poids et mesures: -"The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to 2 x 10–7 newton per metre of length." [math]B®= \frac{\mu_0 I d\mathbf{l} \times \mathbf{r}}{4\pi r^2} = \frac{\mu_0 I}{4\pi r^2}[/math] [math]F= I\int d\boldsymbol{\ell}\times \mathbf{B} = I \mathbf{L} \times \mathbf{B}[/math] r= 1m; dl= 1m; I1=I2= 1A; µ0= 4π*10^-7 -------------------------------------------- B1= µ0/4π* I1/r^2 = 10^-7 * 1/1^2 = 10^-7 B2= µ0/4π* I2/r^2 = 10^-7 * 1/1^2 = 10^-7 F(1-2)= I1 * dl x B2 = 1 * 1 x 10^-7 = 10^-7 F(2-1)= I2 * dl x B1 = 1 * 1 x 10^-7 = 10^-7 --------------------------------------------- F(net) = 2 * 10^-7 N/m :: Check and mate.

I think we understand each other pretty well, considering there are many vague terms involved, that the subject is complicated and that I am not completely explaining my meanings. It's about interpretation, which makes it all more ambiguous, so in short I believe GR is opposite to SR and is compatible with LR, but then LR can not be easily distinguished from SR... which makes it all even more complicated, very hard to differentiate and argue about. I do not have any real point to make about it. Perhaps, it depends, and this is where things start to get interesting. The question is whether magnetic and electric constant are properties of the "vacuum", or properties of quanta/particles, i.e. their electric and magnetic fields and forces. If vacuum permittivity and permeability are not particle properties, if they are really the properties of "vacuum", then in the name of logic this "vacuum" no longer qualifies as "vacua" but as "medium".

What are you talking about, please explain yourself. --- EXAMPLE Q1 ------------------------------------------------------ Wire along x-axis has steady current of 1 ampere, solve for E® and B®. darkenlighten: Do you mean to say this is correct answer? Are these equations valid at all, is that correct derivation of Maxwell's equations? - Do you also mean to agree with him about Biot-Savart law and deny that actually this is the correct expression, where both the full and simplified version can be applied to this problem: Can you solve this example? Can you CLEARLY write down the two equations derived from Maxwell's that actually can solve E® and B® for this scenario, and can you please use CORRECT NOTATION or point some reference? --- CHANGING CURRENT --------------------------------------------------- darkenlighten: Do you mean to say these equations are correct? Do you mean to agree this is true: - "for a changing current there will be an electric field around the wire... E field exists due to a changing B Field"?

I do not mind him at all. It was actually him that made me get involved in this whole discussion. After reading some of his previous threads I thought this was his web page: http://www.proofofabsolutemotion.com/intro.html I thought I can simplify the problem so it can be communicated better and I expected he would surely understand what am I talking about since I actually got inspired by that web-page there, but he did not seem to see any connection and that's where I got confused. In any case, he seem to have figured by now and his latest argument is exactly what I was going to say next. But previously, it was funny to see him arguing against me while I actually came to support his views. Merged post follows: Consecutive posts merged I thought everyone would know about it by now. What year is today? SPEED = DISTANCE/TIME We should never forget this is the only one logical and causal definition. Yes, we can play around with units and re-define everything around the speed of light, but we should never ever forget what velocity really means and what it represents physically. I'm talking about Lorentz Relativity and even General Relativity, do they not describe gravity field as an absolute reference frame? -- If time rate changes as you move through gravity potential, than would you not say it is this gravity potential that defines the speed of light by defining the 'rate of velocity' via defining the 'rate of time'? If gravity can influence time-rate at some space, than gravity is what influences, if not completely defines, the speed in that area of space, including the speed of light, right? On the side note, I understand why there would be MAXIMUM speed, we have maximum velocity of free fall in any medium, it's called 'terminal velocity', but what I do not understand is who did ever say photons can not go any slower than the speed of light?

I do not understand. The example I gave is classic scenario to employ whatever equations you have for velocity vector composition. -- You wanna see if your equations are correct, me too, so can those equations answer my questions? I'm asking my questions to make sure I understand how you equations work, and I do not see why would you hesitate to USE them.

All you had to do is to solve the simplest example we started with. No wonder you got angry. Regarding your example, those equations are wrong and you did not provide any reference for them. http://en.wikipedia.org/wiki/Biot%E2%80%93Savart_law [math]\mathbf{B} = \int\frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{\hat r}}{|r|^2}[/math] * [math]\scriptstyle{\hat{\mathbf{r}}}[/math] is the displacement unit vector in the direction pointing from the wire element towards the point at which the field is being computed * dl is a vector' date=' whose magnitude is the length of the differential element of the wire, and whose direction is the direction of conventional current In our case dl is unit vector too, we are again not doing any integrals as we are again looking at the single point in a single instant in time, it is called "infinitesimal element of wire length". *** THE SIMPLEST EXAMPLE THERE IS: [img']http://dev.physicslab.org/img/2162109e-eb6e-4193-8e52-9d141f928e92.gif[/img] Q1: Magnitude of E filed at distance 'r' can change with varying current? Q2: Magnitude of E filed at distance 'r' can change with changing B field? Q3: Magnitude of E filed at distance 'r' can change with moving magnets? darkenlighten: - "for a changing current there will be an electric field around the wire" - "...E field exists due to a changing B Field" You could just as well said pigs have wings. Wires do not change their electrical neutrality around them due to any changes in current, motion of any magnets or due to change of any magnetic fields. Voltage, my young friend, you are not talking about any "time-varying E field" as there is no such thing, you are talking about "potential difference" and "electric current" - distribution and electron kinetics, these particular effects are not measured at any point AROUND the wire, and these you should not call "E field". Ay, caramba! Concentrate on your part and provide solution via Maxwell's equations, if you can. In the very next message I put back that term in Biot-Savart law you were complaining about to avoid silly arguments and embarrass you further... P P' | | r= distance(AP) | | |angle= AW-AP = 90 ----------------A---------------------B-------wire W---> Of course if we place 'probe' at point P we are measuring the magnitude in relation to wire at point A. It is ridiculous that someone would try to measure field potential around the wire at some distance 'r' by placing the instrument at point P and thinking it will measure the magnitude in relation to point/segment B that is further away from the instrument, that's just utter nonsense - it's equivalent of trying to measure your own body temperature by placing the thermometer not up yours, but up someone else's... armpit. P |\ | \ r' | \ |r \ | \ ----------------A-----B-----------------wire W---> In my example I assume laws of logic still hold and people are sane. In my example when I say distance 'r', it, OF COURSE, means distance A-P, the SHORTEST DISTANCE. No sane person would ever measure the DISTANCE from a straight wire at any other angle but 90 degrees. Distance is the shortest path between two points, ok? Do you not see what is 'angle', what is 'dl' and what is 'r'? Steady 1 ampere, what is E® & B®?

I'm asking for the reference to the formulas you supposedly derived from Maxwell's equations and you believe are solutions for this PARTICULAR EXAMPLE: Q1: Wire positioned along x-axis has steady current of 1 ampere' date=' solve for E® and B®. [img']http://www.scienceforums.net/forum/latex/img/9cca7d2d3cbb94a9a0238c6a71db0590-1.gif[/img] Do you say this the solution for THIS PARTICULAR EXAMPLE? No? What is it then? Can you solve THIS SIMPLEST EXAMPLE?

What then' date=' write it down already. You wrote 4-5 different formulas, some of them proved to be wrong and all of them contradicting each other, violate logic and deny common experience, so which one? You failed at simplest example with point charges and now we are talking about the most basic case scenario with infinite wires, what's problem? [b']Q1: Wire positioned along x-axis has steady current of 1 ampere, solve for E® and B®.[/b] *PROVIDE REFERENCE

Ok. In any case, my point is that any experiments where measurements are not taken with some velocity relative to ground (airplanes, trains, satellites) can not prove anything about anything simply because "Aether" everyone is talking about is the same thing what we already call 'gravity field'. http://en.wikipedia.org/wiki/Electromagnetic_wave_equation - "Time dilation in transversal motion. The requirement that the speed of light is constant in every inertial reference frame leads to the theory of Special Relativity." -- What I was talking about is mostly known as 'aberration effect' and is fundamental to measuring and analyzing the speed of light. =Static sensor ======B ..b1 ..b2 ..b3 ..b4 ===== | | E------------------->A-------> Moving emitter Photon emitter 'E' moves from left to right with arbitrary constant velocity. When E passes over point 'A' it shoots a single photon in the direction of 'B'. Q: The faster E moves, the further away from B(b1, b2, b3..) photon hits the sensor? A: YES, the faster a frame moves, the more the angle in a stationary frame. Q: The faster E moves, the more time photon takes to cross AB distance and hits sensor? A: YES/NO?

Are QM equations based on Coulomb's force and properties of electric fields? Is there apparent relation of orbitals and inverse square law in QM equations? From Bohr model it seems the charges in atom orbitals still obey known forces? E field conserve energy, exchange is between potential and kinetic energy only?

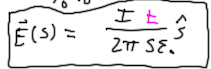
The former is known as 'ignorance', it qualifies the later as 'arrogance'. Even if you derived those equations properly they would still give DIFFERENT results than Biot-Savart and Coulomb's law, just because of *different* constants and distance relation. Wire positioned along x-axis has steady current of 1 ampere, solve for E® and B®. COULOMB vs. "MAXWELL" by darkenlighten: [math] E = {1 \over 4\pi\varepsilon_0}{Q_{net}\over r^2}[/math] -VS- [math]E = \frac{\mu_0 I}{4 \pi}\hat{r} [/math] BIOT-SAVART vs. "MAXWELL" by darkenlighten: [math]B = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{\hat r}}{r^2}[/math] -VS- [math]B = \frac{\mu_0}{2\pi} \frac{I}{r}\hat{r}[/math] E field at point 'r' can change with varying current, change in voltage, or moving magnets around the wire? -- If you think I do not represent Biot-Savart and Coulomb's law correctly for THIS PARTICULAR example and/or if you think I misinterpreted "your" equations, then go ahead and finally write the "correct" solutions already yourself, get rid of the 'Phi' and spherical coordinates so we can COMPARE the equations properly. Merged post follows: Consecutive posts merged Stop wasting everyone's time, that's embarrassing. You are making it only worse for Maxwell because you do not have that term in there at all, and I just got it out because it equals to -ONE- for this particular case scenario. - Logically, and obviously from the illustration, in the case with wires the distance vector is always at 90 degrees to wires, so: dl x r = sin(90) = 1 [math]B®= \frac{\mu_0 I d\mathbf{l} \times \mathbf{r}}{4\pi r^2} = \frac{\mu_0 I sin(angle)}{4\pi r^2} = \frac{\mu_0 I sin(90)}{4\pi r^2} = \frac{\mu_0 I * 1}{4\pi r^2} = \frac{\mu_0 I}{4\pi r^2}[/math] Magnitude of E filed at distance 'r' can change with frequency? Stop hallucinating equations and dreaming up nonsense. We are COMPARING two different sets of equation by trying to apply them on the same scenario and get them in THE SAME FORMAT. -- You have lost all your credibility, I will not consider any more empty arguments from you without some reference provided and equations written in proper and comparable format. Magnitude of E filed at distance 'r' can change with changing B field? What "E field" are you talking about? Where and how do we measure it?

Wire positioned along x-axis has steady current of 1 ampere, solve for E® and B®. I was, of course, referring to Biot-Savart and Coulomb's law where these constants are COMPLETELY UNNECESSARY. The point was those constants in Biot-Savart and Coulomb's law are there because of Maxwell's equations, which is to say - for no good reason. Take the example above, the one we are already talking about, then take some magnet and move it around that wire any way you want. There will be dB/dt, but what E field do you think would change - where and how would you measure it? I really want to know what is this "E field" you are talking about in terms of measurement, instruments and in what units is that "E field" of yours, especially since we just previously concluded there will be no electric field around the wire due to superposition of positively charged nucleus in the wire, regardless of any change in current or application of voltage, didn't we? We are already talking about that scenario, with straight wire along x-axis and steady current of 1 ampere, we said there will be no electric field around it due to superposition, so what in the world is "cos(wt)" and what any angles have to do with E field? a.) "Fi" is "flux" symbol in these equations, you need to use "dl" to denote the direction of electric current, is your "Fi" a unit vector or variable magnitude? b.) Are you saying it's "m0/2Pi" and not "m0/4Pi"? Distance is not squared? c.) Do you not see that your dB/dt equals to zero, actually, and what does it take for you to realize there will be no E field around the wire regardless of current, voltage or any change in any magnetic fields? Ay, caramba! Is that magnetic or electric constant? What field are you talking about, "around the wire" or something else? Wires are made of neutrally charged atoms - superposition of positive and negative charges is what keeps it all electrically neutral regardless of any B or dB/dt and amperes and voltage, only position, i.e DISTRIBUTION of E fields/charges is what matters: (-q +q), and no B fields go into this vector addition calculus, ok? E= Ke* (-q+q)/r*2 What you did is hideous, you completely removed the distance!!?! You have no idea what E filed you are talking about, without the distance what would you measure, where? - Your conclusions are completely devoid of any practical and experimental linkage, you are still yet do differentiate between the basic terms and their physical meaning, like charge, potential, voltage, current, and what "field(s)" have to do with any of that, in real world.

Thanks. That is exactly what anyone should do before engaging into argument - define the terms and make sure both sides understand each other exactly and are actually talking about the same thing. So, let us quickly jump to the very beginning, how do you interpret what Einstein himself said: - Any ray of light moves in THE “stationary”* system of coordinates with determined velocity c, whether the ray be emitted by a stationary or by a moving body. *Stationary: Let us take a system of coordinates in which the equations of newtonian mechanics hold good. In order to render our presentation more precise and to distinguish this system of coordinates verbally from others that will be introduced hereafter, we call it the “stationary system”. MEANING: Photons have constant velocity 'c' relative to Earth... ...or whatever planet you're standing on (Newtonian mechanics holds good)?! Einstein does not even mention "all" frames or "any" frames, nor any relations between some different frames, he defines the speed of light as relative to just one, very privileged frame - THE "static" frame. No other frames are mentioned there and what else -"where Newtonian mechanics holds good"- can mean?

Ke=1/4Pi*e0 Coulomb's law: E= Ke* (-q+q)/r^2 Km=m0/4Pi Biot-Savart law:B= Km* I/r^2 -simplification without "dlxR", as distance is measured at right angle ================================================== Ok, let's now look at those constants - what in the world is "4Pi" doing there? It seem arbitrary in these equations as they already describe spherical geometry without it, it's an unnecessary scalar in this vector equation, how did it get there? In any case, we should note the whole term "4Pi*r^2" is the description of 'surface area of a sphere', i.e. A= 4Pi*r^2. 1.) ELECTRIC FIELDS 1st: divE= p/e0 3rd: rotE= -dB/dt ------------------ First time you gave us something like Coulomb's law, so please decide and write down what is the final equation for E field you are offering as the solution for this example, I'm not sure if your distance there is inverse squared or not. In any case there is something strange about the 3rd one, where do we see E field depend on the change of B field, and how can this 3rd equation do anything without either magnetic or electric constant? Are there not any examples where we can use this 3rd (and 2nd) equation? 2.) Magnetic fields 2nd: divB= 0 4th: rotB= J + dE/dt --------------------- Where, why and how do we ever use 2nd equation and how can it work without magnetic constant? Anyhow, here is this 4th equation and we finally have some real answers, so let's see if those make any sense... a.) "Are we talking about the same fields?" MAXWELL: B= m0/2Pi * I/r BIOT-SAVART: B= m0/4Pi * I/r^2 "2Pi" is not the same as "4pi" and "r" is not the same as "r^2". What we have here is 'circumference of a circle': C= 2Pi*r, versus 'surface area of a sphere': A= 4Pi*r^2. This again points to "two-dimensionality" of these equations, but most importantly the two formulas are not IDENTICAL, so which one is wrong? b.) "That same old equation for loops, again." - Your equation in its original form actually has some "time-varying" terms in it, so how and why did you pick that one to start with, since we have a 'steady current' in our example? - Did you start with "Formulation in terms of FREE charge and current" or "Formulation in terms of TOTAL charge and current" and how did you make the decision which one suits this example better - are we dealing here with "displacement current: dD/dt", or with "time-varying electric field" dE/dt"? How to obtain the value for "dD/dt" and/or "dE/dt", what is their physical meaning and what do these terms represent in our example? ============================================ BY THE WAY, why is this important? This is exactly what defines the unit of Ampere, that's why, it is actually this magnetic field that goes all the way around and back to bait its tail and define both electricity and magnetism. All this got even more complicated as the units got redefined ("Rationalized") over time and many things became self-referenced and circularly defined. So, electric aka *Coulomb force constant* and magnetic constant lost their physical meaning as experimentally determined values and now it is almost as if they jumped out of Maxwell's equations... EM WAVES: On Physical Lines of Force, by James Clerk Maxwell http://books.google.co.nz/books?id=duyKrTNps_AC&lpg=PA451&dq=%22on%20physical%20lines%20of%20force%22&pg=PA495#v=onepage&q=&f=false - "To find the relation between electromotive force... The ratio of m to mu varies in different substances; but in a medium whose elasticity depend entirely upon forces acting between pairs of particles, this ratio is that of 6 to 5, and in this case E^2= Pi*m ...(108)" http://books.google.co.nz/books?id=duyKrTNps_AC&lpg=PA451&dq=%22on%20physical%20lines%20of%20force%22&pg=PA499#v=onepage&q=&f=false -"To find the rate of propagation of transverse vibrations through the elastic medium of which the cells are composed, on the supposition that its elasticity is due entirely to forces acting between pairs of particles. V^2= m/p ...(132), where 'm' is the coefficient of transverse elasticity, and 'p' is the density. mu= Pi*p ...(133) Pi*m= V^2*mu ...(134) E= V* sqrt(mu) ...(135), and by (108: E^2= Pi*m), In air or vacuum mu=1, and therefore V = E, = 310,740,000,000 millimeters per second ...(136)." What the...? Ratio 6:5?!? -- Where is the "curl of the curl"? Does anyone recognize that equation used to get to the speed of light? - "The speed of propagation of a wave in a string (v) is proportional to the square root of the TENSION of the string (T) and inversely proportional to the square root of the linear mass (μ) of the string (DENSITY)." http://en.wikipedia.org/wiki/Vibrating_string Hmmm, so these are the 'boundary conditions' - "vibrating string"? Funny enough, to me this makes much more sense than how this derivation is interpreted today with "curl of the curl" thing, and I especially like the part about *pairs* of particles, it's as if he is talking about electron-positron pairs too - "dielectric"/"polarized". However, the final calculation... I have no idea how did he get that number and those units - can anyone make sense as what values did he plug in and where did he get those numbers from? Was this the origin of electric and magnetic constant - elasticity and density?

Hmmm, these are the questions: Q1: What do you believe is correct diagram, 1st or 2nd one? Q2: What do you believe Einstein believed is correct diagram, 1st or 2nd?

Everything except emitter is static relative to ground and everything is measured in this 'static' frame of reference called Earth. -- This has everything to do with this thread and with every other discussion about the speed of light. You should eventually realize once you answer the last question too. =Static sensor ======B ..b1 ..b2 ..b3 ..b4 ===== | | E------------------->A-------> Moving emitter Photon emitter 'E' moves from left to right with arbitrary constant velocity. When E passes over point 'A' it shoots a single photon in the direction of 'B'. [/Code] Q: The faster E moves, the further away from B(b1, b2, b3..) photon hits the sensor? A: YES, the faster a frame moves, the more the angle in a stationary frame. Q: The faster E moves, the more time photon takes to cross AB distance and hits sensor? A: YES/NO, "measured path" is supposed to always be c regardless. (?) "supposed"? Can you answer the question please, yes/no? -- Hopefully after answering that question you will be fully aware how this has everything to do with SR and with this thread in particular. You are representing the "aether theory", aren't you? You want to prove the speed of light is not actually constant in all reference frames as SR says, right? - Do you know what is the sped of light relative to? - Does absolute speed require absolute reference frame?

Of course it's SR, and it is exactly the same thing as what you have been talking about in all your previous threads. Anyhow, can you answer those three questions or not? Those are 'yes/no' questions, should be easy.

Please use some printed and readable pictures or plain text and/or symbols. I'd rather you do not do any derivations any more, but simply write down the final equation exactly as required, or copy/paste somewhere from the internet, or point to proper reference. Constants: Ke= 1/4Pi*e0 ; Km= m0/4Pi E®= Ke* (-q+q)/r^2 B®= Km* I/r^2 ======================================== YOUR EQUATION: E®= Ke* I(t)/r ?? What is that red "t", how do I "plug" that in, what is that? Please get out of cylindrical coordinates and tell us if your distance is inverse squared or not? -- There will be no electric field around wire because conductors are macroscopically electrically neutral due to superposition, as there is about equal amount of negative and positive charges in close proximity, so wires have net zero external electric charge, regrades of any current and voltage applied. That's how crazy formulas can make you blind even to the most obvious everyday experience. YOUR EQUATION: B®= Km* I*Fi/r ?? Is that "Fi" for flux, how do I "plug" in that one? I believe this below is what you meant to say, but that is still not Biot-Savart law. http://dev.physicslab.org/Document.aspx?doctype=3&filename=Magnetism_BiotSavartLaw.xml http://dev.physicslab.org/Document.aspx?doctype=3&filename=Magnetism_AmperesLaw.xml

I can help resolve this argument, or at least make it less ambiguous. The greatest problem here is that people believe to be talking about the same thing while actually thinking about completely different concepts, and I have simple example that can very distinctively separate who is actually saying what about the speed and properties of light, exactly. =Sensor =============B ..b1 ..b2 ..b3 ..b4 ===== | | E------------------->A-------> Photon emitter 'E' moves from left to right with arbitrary constant velocity. When E passes over point 'A' it shoots a single photon in the direction of 'B'. 1.) The faster E moves, the greater energy sensor will register upon the impact? 2.) The faster E moves, the further away from B(b1, b2, b3..) photon hits the sensor? 3.) The faster E moves, the more time photon takes to cross AB distance and hits sensor?

http://en.wikipedia.org/wiki/Biot-savart_law -"The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant. The law is valid in the magnetostatic approximation, and results in a B field consistent with both Ampère's circuital law and Gauss's law for magnetism." Your demonstration so far suggests you have not used any of those equations, ever. You need to realize these two sets of equations must be strictly IDENTICAL as they are describing the same fields and same interaction. So, for example, if 2nd Maxwell's equation does not equal to Biot-Savart law, then one of them is wrong or not complete, and you will never realize which one if you do not start USING them. Q1: Wire W1 positioned along x-axis has steady current of 1 ampere, what is the magnitude of E and B field at some arbitrary distance, solve for E® and B®? Q2: When and what for is the 2nd equation used then, one example please? Q3: Wire W1 positioned along x-axis has a steady current of 1 ampere, the second wire W2 has no current or voltage directly applied to it and is always parallel to W1, it can only move along y-axis so to get closer and further away from W1 while them staying perfectly parallel. -- Now, if wire W2 moves with constant velocity of 25m/s from the distance 2.5m to 0.5m towards the wire W1, describe how dB and dE in these two wires vary with the time and solve for the total amount of E and B fields induced in wire W2 during this motion. Nonsense, time is only a consequence of motion. E fields never ever vary, which is why we say electric charge is quantized and constant. The closest thing to what you're saying is that B fields vary with VELOCITY, where the spatial change is the actual causal link, not the time. In any case nothing else varies about these fields, ever, except their relative distance. Let's see... when we smash positron and electron together we get photon, and when we smash photons apart we get positron-electron pairs. I already told you how I got "em waves" with Lorentz force and with no boundary conditions, but with INITIAL CONDITIONS. I did not "force" these two charges to twirl and oscillate around each other as transverse waves, that was written in the Coulomb's, Biot-Savart-Law and Lorentz force long time ago, and still is, see for yourself. http://en.wikipedia.org/wiki/Light_polarization It looks exactly like this, except there is one more charge (opposite) whose trajectory mirrors the blue path pictured here, and is actually THE REASON why would any electric fields move like that - up/down and/or left/right - there are actually two of them orbiting each other. Q4: Are you suggesting the change in electron's own B field induces changes in its own E field, and the other way around? What do you think how many separate E and B fields are there in one photon in any single instant in time?

Ok, I went through "091117.pdf" and I see many familiar things there. Let me study it a bit and I'll give you my opinion about it. There is nothing new in "my idea", I'm doing electron orbitals just like planetary orbits, with Newton's laws of motion and kinematics equations using Coulomb's force instead of Newton's gravity equation. What I am doing differently than anyone else, ever, is that I included MAGNETIC interaction too and I'm doing it in 3D, dynamically not statistically, so with magnetic fields these start to look differently than planetary orbits and you get electrons to attract due to magnetic force when you expected them to repel due to electric force - given certain orientation, distance and velocity - and hence classical electrodynamics predicts electron coupling, which I believe has to do with Pauli exclusion principle and what not. I explained much of what I do here in this thread, where the most interesting thing is classical prediction of electron-positron helical trajectories that look exactly as one would expect electromagnetic wave (photon) to look and behave, including net el. charge of zero and ability to polarize their plane of oscillation either linearly or circularly: http://www.scienceforums.net/forum/showthread.php?t=50010&page=2 Merged post follows: Consecutive posts merged Ok, we are doing almost the same thing. The difference is I do not want to be considering any additional effects like radiation until I can get all the *classical* dynamics in there first. I'm talking about magnetic spin dipole moment, which I can not properly simulate. I hope some clever experiment might give me some idea how to include this 2nd magnetic interaction due to spin dipole moment, at least as approximation, and only then if I do not get accurate atomic model, only then will I seek to include radiation or whatever additional effect and new physics. So, my advice would be to drop all of the Maxwell's equations as they can not deal with point charges, concentrate on Coulomb's law, Biot-Savart law and Lorentz force. But, in any case we are both left with the same problem in either case - MAGNETIC SPIN DIPOLE MOMENT - very, very hard to account for and yet it may have some significant contribution to the whole affair that is going on within "electron cloud". For example this spin dipole interaction may be what is causing what you call "pinch". What are the average velocities you get for electrons in different orbitals?

You see almost empty glass as a half-full. I would not say "anything", but only certain specific things with high symmetry, such as loops and infinite wires, but that's pretty much it, and everything else is approximation based on either that loop or infinite wire. So, we have this important law for magnetism that is not used to solve for the magnetic fields? What then, what is it used for? -- You are giving me that equation for LOOPS, again?!? "No, no, no" to you. There is no induction in our example, there is only one charge/electron there. Are you suggesting the change in electron's own B field induces changes in its own E field, and the other way around?