Cap'n Refsmmat

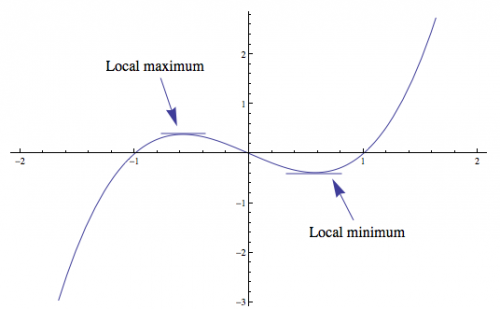
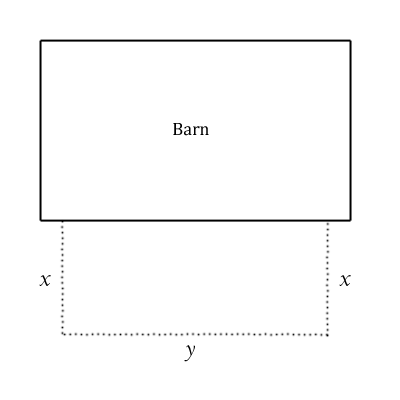
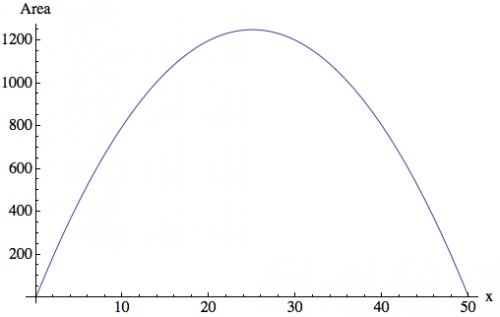
Lesson 8: Basic Applications: Finding the Maximum and Minimum Values of a Function: This lesson was contributed by SFN member Daedalus, who did an excellent job putting it together. If you find this helpful, be sure to thank Daedalus! The derivative of a function defines the slope of a line tangent to the curve. Normally, derivatives are used in calculations where the rate of change is needed. However, the derivative can also be used to find the extremum (singular) or extrema (plural) of a function. There are two types of extrema called the global extrema and local extrema. The global extrema defines the overall maximum and / or minimum value(s) in the range of a function. The local extrema, sometimes referred to as the relative extrema, defines the maximum and / or minimum value(s) in the range of a function within a given region. To find the extrema of a function, we must find the stationary points of a function where a horizontal line is tangent to the curve. This involves finding the roots of the first derivative which is the same as setting the first derivative equal to zero and solving for [math]x[/math]. [math]f'(x)=0[/math] A stationary point may be the minimum, maximum, or an inflection point on the curve. We can see that in this example: The labeled points have slopes of zero (as shown by the tangent lines) and show where the function "flattens out." This happens at minima and maxima, but also at inflection points, where the function increases, stops, then increases again (or the reverse). To make sure that we have found the extrema, we can use the first derivative test which states: For any stationary point [math]x_{s}[/math] on a continuous function [math]f(x)[/math] we can determine if the stationary point is a minimum, maximum, or inflection point of the function according to the following rules: Local Minimum (Possibly Global): [math]f'(x)<0[/math] to the left of [math]x_{s}[/math] and [math]f'(x)>0[/math] to the right. Local Maximum (Possibly Global): [math]f'(x)>0[/math] to the left of [math]x_{s}[/math] and [math]f'(x)<0[/math] to the right. Inflection Point: The sign of [math]f'(x)[/math] is the same on both sides of [math]x_{s}[/math]. Applying The Derivative: Now that we have discussed how to find the extrema of a function, we will apply this knowledge to solve a problem that anyone who grows a garden will appreciate. A farmer has decided to plant a garden and would like to build a fence around it to keep the animals from eating the crops. Being an experienced farmer, he decided to place the garden up against his barn because he only has 100 ft of fence and he wants to enclose the largest possible area. The following image illustrates the problem: We can see that the area of the garden is defined by: [math]A=x \times y [/math] We can also see that the perimeter of the fence is equal to: [math]P=2\, x + y[/math] However, the equation for the area of the garden is not in a form that is useful to us. We'd like the equation in a form that only uses one variable, to make it easier to work with. Let's use the variable [math]x[/math]. If we look at the equation for the perimeter of the fence, we can solve for [math]y[/math] and substitute that result into the equation for the area of the garden: [math]y=P - 2\, x[/math] Replacing the variable [math]y[/math] with [math]P-2\, x[/math] in the equation for the area of the garden yields: [math]A=x \, (P - 2\, x) = x\, P - 2\, x^2[/math] Now, as stated in the problem, we know the farmer has 100 feet of fence to work with, so [math]P=100[/math]. We can see there are many possible areas for the garden, depending on the length of the sides -- there could be a very long, skinny garden with almost no space, or a broad garden with plenty of space. If we plot [math]A[/math], we see that it forms a parabola: However, we are only interested in the largest possible area that can be enclosed by the fence. This means we must find the number [math]x[/math] which gives the maximum value of [math]A[/math] in our function. To do this we will locate our stationary point(s) by taking the first derivative of our function, setting it equal to zero, and solving for [math]x[/math]: The derivative of our area function as provided by the power rule: [math]A'(x)=P - 4\, x[/math] We search for horizontal tangents by setting [math]A'(x)=0[/math]: [math]P - 4\, x=0[/math] Solving for [math]x[/math]: [math]x=\frac{P}{4}[/math] We can check this point to see if it is the maximum by using the first derivative test: [math]P- 4\, \left (\frac{P}{4} - 0.01\right) = 0.04[/math] [math]P- 4\, \left (\frac{P}{4} + 0.01\right) = -0.04[/math] The stationary point is indeed the maximum because the slope to the left of the stationary point is positive and the slope to the right is negative. (That is, the function goes up, reaches this maximum point, and then goes down -- it doesn't go up again.) Furthermore, by looking at the graph we can conclude that this stationary point is the global maximum of the function, since it only goes down on each side. We know that the farmer only has 100 ft. of fence which is equal to the perimeter that we have defined in the equations. With [math]P=100 \mbox{ft}[/math], we can let the farmer know that the width of his garden needs to be [math]25 \mbox{ft}[/math] : [math]\frac{P}{4}=\frac{100 \mbox{ft}}{4}=25 \mbox{ft}[/math] The length of his garden needs to be [math]50\mbox{ft}[/math] : [math]y=P - 2\, x=100 \mbox{ft} - 2\, (25 \mbox{ft})= 50 \mbox{ft}[/math] This gives the farmer a maximum [math]1250 \mbox{ft}^2[/math] of area to plant his garden : [math]x \times y=25 \mbox{ft} \times 50 \mbox{ft}=1250 \mbox{ft}^2[/math] or [math]x \times y=\frac{P}{4} \times \left(P-2\, \left(\frac{P}{4}\right)\right)=\frac{P^2}{8}=\frac{10000 \mbox{ft}^2}{8}=1250 \mbox{ft}^2[/math] Exercises for The Reader: If the farmer decided to place his garden away from the barn such that he had to use the entire length of fence to enclose the garden (rather than letting one wall of the barn fence in the garden), what would be the maximum area he could enclose? Would this area be a rectangle or would it be a square?

If this is your conclusion, then you do not yet understand the nature of relativity and how it works. Likewise with the arguments about the shape of the Earth and the nature of 4D spacetime. It's clear you do not want to learn from me, but rather to contradict everything I say, so I don't see the point of explaining. Physics does not require theories to avoid absurdity; nature has no such qualms. I'd hate to be around when you read about quantum mechanics.

Atomic clocks don't measure the lifetimes of atoms or particles. Why do hourglasses and spring clocks measure the passage of time, but atomic decay does not?

Why spring clocks and hourglasses rather than atomic clocks?

Plenty of places for reason; physics is based on it. "Common sense" is unfortunately a poor predictor of the nature of the universe. Appeal to ridicule isn't an argument against experimental evidence. And I say I'm not a textbook. You need one to get a full explanation, unless you'd like to wait around for a few weeks while I write one.

Please do. I'm not going to bother answering so many questions when they are essentially "but if I throw out all the important parts of relativity, it's so absurd!" You can't, say, ditch 4D spacetime and then expect relativity to make very much sense.

Do you really think they're advocating simple wealth redistribution? It seems to me the analogous situation would be "they feel straight A students whose parents donated money to endow the professor's chair and fund his research don't deserve their straight As, and are conspiring to ruin the curve for the rest of the students." Whether or not that's a true allegation is another matter -- but let's get their allegations straight before we judge them.

The Super Proton Synchrotron is used to create the neutrino beam, since they don't need the incredibly high energies of the LHC just to make neutrinos. The SPS has been in operation since the 70s.

The neutrino experiment did not use the LHC. Unfortunately there are no particles other than neutrinos which will penetrate through several hundred miles of earth and still reach the target.

I think one of their premises is that it is impossible to be elected without becoming one of "them," as a result of the state of campaign finance, so holding representatives accountable at elections is impossible. If any candidate with sufficient support to win is already beholden to "them" via campaign donations, endorsements, and so on, what's the point? Not that I know they haven't voted; it's quite possible that many of the protesters voted in the past. But if they choose to express their newfound interest in politics as protests, why is that bad? It is a strategy to raise awareness of an issue to (a) spark public debate, hopefully influencing policy and (b) gather supporters, ideally influencing elections.

Rotating coordinates in four-dimensional spacetime causes space and time to "mix", making events which were far apart in time and close together in space become closer in time and farther in space, and so on. This can be used to explain all observed relativistic effects. However, I am not a textbook. I suggest you get one if you wish to learn the nature of Minkowski space. Your overall philosophy of realism relies on the single assumption that these properties are intrinsic in three dimensions, which is the only assumption which must be thrown out. The rest of the philosophy can stay. I regret that evolution has not provided you with eyes which can see in the fourth dimension. It's real enough for the particles in the accelerator to behave very differently than they would in their "real" shape. If the "real" shape cannot explain the results of the experiment, what good is it?

Er. That's not how length contraction is measured in a particle accelerator at all. Here's a few resources you can look over: http://www.physicsforums.com/showthread.php?t=299618 http://www2.slac.stanford.edu/vvc/theory/relativity.html http://books.google.com/books?id=o4dc_zcnl1cC&pg=PA296&lpg=PA296&dq=feynman+pancake+particle&source=bl&ots=zF5thdnWqZ&sig=eCMAhKbn6Cv__5RnIIlcPPulAWU&hl=en&ei=FvaMTrqtG5CKsAKvzOjeBA&sa=X&oi=book_result&ct=result&resnum=2&sqi=2&ved=0CB8Q6AEwAQ#v=onepage&q=feynman%20pancake%20particle&f=false Very consistent, when you include it in the set of ideas that constitute modern physics, such as 4D Minkowski space. Clearly inconsistent when you contrast it with the beliefs you personally hold.

Fascinating. Length contraction and time dilation were devised as ways to make things logically consistent after the constant speed of light was accepted. They are direct consequences. My boss is a particle physicist. Anything you want to ask him?

Yes, there's optical interferometry: http://en.wikipedia.org/wiki/VLT The trouble is that it's difficult to accurately combine light beams that are received a large distance apart.

Light moves at the speed of light relative to any observer, and you agreed that the experiments demonstrate this. So your version of events has been experimentally demonstrated to be impossible.

So the rules depend on whether you're doing addition and subtraction or multiplication and division. If I take two numbers and multiply them, the final result must have the same number of significant digits as the least precise initial term: [math]55.7 \times 432.678 = 24100[/math] If I take two numbers and subtract or add them, the final result must have the same number of decimal places as the initial term with the fewest decimal places: [math]55.7 - 32.468 = 23.2[/math] Interim results should be kept to full precision, and you should only round your final results. I'm actually not sure how this applies to compound expressions like the example you gave. I think you've done the right thing, but I'm not entirely sure.

Surely they have it backwards; if theory says neutrinos can't be superluminal, and they have not found a systematic error in the data, then the theory is wrong. I could just as easily write a paper saying "special relativity means they could never be superluminal in the first place, so I've refuted the result", but the point of the result is that it might break SR.

Yes, generally one performs the intermediate steps keeping all of the digits (as much precision as possible), and only rounds the final answer.

Science knows exactly what shape an observer will measure the Earth to be. It can predict that mathematically with excellent precision. It's not like relativity permits an observer to fly past and discover that the Earth is now in the shape of a half-eaten jelly doughnut. There are certain rules. So you're saying that the person holding the flashlight will measure the velocity of the light beam as 1/2 c relative to him? That's what this seems to imply.

The phrasing "drastically change shape" implies that an observer will be looking at Earth and watch in amazement as it squashes itself flat. That doesn't happen. However, different observers will not agree on the Earth's shape, and that's not particularly worrisome to me. At no point have I disagreed with swansont or Schrodinger's Hat. Here's the question I hoped you could answer: http://www.scienceforums.net/topic/58293-frame-of-reference-as-subject-in-subjective-idealism/page__view__findpost__p__629154

Well, that's unfortunate. Maybe you could answer md65536's recent question, then.

I can exactly describe the "true shape" of our home planet. It just happens to live in four dimensions. The absurdity you point out is entirely normal.

That's how I explained it, yes. From an observer's point of you, the light source is moving at half the speed of light, so it "chases" the projected light beam. In one second, the light moves half a light-second away from the flashlight, since the flashlight is chasing it. Now, what does the light source observe? From the light source's perspective, it's not moving -- if you measure your velocity relative to yourself, you get 0. After one second, how far away is the light? Any well-done measurement is accurate in that reference frame. It just disagrees with other accurate measurements taken in other reference frames. Ha. I can explain the course of this thread via a simple analogy: Us: Let's explain how to make an omelet. First, you crack a few eggs into a bowl. You: What?! I'm not eating raw eggs! That's disgusting! Us: ...no, no, they won't be raw when we-- You: That makes no sense. Look. Imagine I put some raw eggs in a bowl and leave for an hour. When I come back, they'll still be raw. Right? Us: ...yes, but we're going to cook-- You: How can eggs be both cooked and uncooked? That's nonsense! Realism demands eggs be either one or the other. Anything else is a result of drinking too much cooking sherry. Us: But they're never both cooked and uncooked -- they're raw at one time, and cooked later. You: No, that's not what I see in my example. Put some raw eggs in a bowl and they stay raw. Us: Right, but you can cook them. You: So now the eggs are both cooked and uncooked, are they? Us: Uhm, no. You: You're absurd. If you'd let us cook the eggs, you might understand.

At no point in my diagrams (or anyone's diagrams, I think) was light pushed faster than c in any reference frames. Could you point to an example where it was?

You can enclose your text in [/noparse] tags and it'll render in monospaced font, with all spaces retained. Example: [noparse] Penguin Walrus Penguin Walrus