md65536

Hrm, I guess I can see how that could be useful. The intersection of any of 1-odd, 2-odd, 3-odd, etc is empty. But does that get you anywhere toward proving that all odd numbers are covered by those sets? Is it possible to determine the cardinality of all infinity of those sets up to a given limit N, and show that it's equal to N/2? Is there a formula for the cardinality of the sets? They have infinite dimensions but can't you map the multiple dimensions to 1 using the "diagonal processing" method (http://www.proofwiki.org/wiki/Cartesian_Product_of_Countable_Sets_is_Countable)?

Oh jeez... it certainly won't be me! ...not unless I invent a new form of math that I understand better than normal maths, or I get zapped by a Cytherian probe and then Geordi gets all jealous when I'm super smart. I'll explain a bit how I solved it to show it didn't require difficult math. First of all I made a list of "1-odd" (ignoring whether odd or even), which are {1, 2, 4, 8, 16, ...}, and realized that any in 2-odd must be one of those numbers x, less one, divided by 3. That is, keep any where x-1 is divisible by 3. Here's where I started CHEATING ... I put it all in a Libreoffice spreadsheet and made a grid of numbers to look for patterns. Then the pattern where alternating numbers are divisible is readily apparent. However you can easily prove that the pattern will continue, because if x-1 = 3b for some natural b, then 4x-1 = 4(3b+1)-1 = 12b+3 is divisible by 3, but 2x-1 = 6b+1 is clearly not. Then repeat the reasoning... 3-odd must be one of 2-odd, multiplied by some 2^j, minus 1 divided by 3, and then only if it's divisible by 3. So I made a 2d grid with increasing values of i and j and filled it with a naive formula that didn't care if it was divisible or not, and looked for patterns. The non-divisible ones have a bunch of decimal places. Here the "every third row is integral" pattern shows up, and you can again easily prove that that pattern continues. I think I accidentally copied the "skip every second value" and put in the wrong formula, which is why I missed the second formula (but I think I lucked out because the grid with all of the values in it looks too hard to figure out. I would have been stuck, looking for a single equation). After Daedalus corrected me I just wrote out the 113 sequence and fiddled with the formula until it produced it. :S Once the simple "every third value of i works" pattern is established, you just have to multiply i by 3 with the correct offset. Being able to find the pattern with brute force is one thing, being able to show that it works for all values is pretty good I guess, but understanding why it works is another thing! After Daedalus' explanation I can almost uh... imagine understanding it.

Yes, I'm probably thinking about tipped cones the wrong way. The EH is a lightlike surface. It is only locally that the speed of the EH is equal to the local speed of light, and locally the observer is at rest. It's like saying "light travels at c relative to me" but it makes no sense to say "This implies that I travel past photons at the speed of light." Being a lightlike surface, you can't speak of your velocity relative to it in local coordinates (where it is moving at the local speed of light). I think reading this comment: http://www.physicsforums.com/showthread.php?p=4378646#post4378646 and some after it, that made it make sense to me.

Oh boy... I think it's safe! I've thought of this conjecture a few times over the years, never with this much mathematical analysis. When I first heard of it, it was presented as an algorithm to demonstrate the idea of processes that you couldn't say whether or not would terminate. I think a prof said something like, if you can prove that it would (or not) on every input, you'd become rich. So it piqued my interest! I think the prof also said that to prove it would likely require a whole new type of math, which is interesting because new types of math are sometimes invented to deal with physical problems (eg. calculus). As we understand the world in greater details and scales, we need new maths to describe it. The way that I imagine this conjecture being proved is through some kind of quantum computer algorithm, using superposition... If you could define mathematical operators that represent the results of both operations (x/2 or 3x+1) at the same time, and then are able to analyze the results of infinite iterations of the operator, then you might be able to prove it?

To expand on that... Memory is addressable by individual bytes. Each byte of memory has an "address" which is basically a binary number. If you have 20 address lines (wires) connected to the chip, you can have 2^20 (about a million) different addresses. I guess it wouldn't make much sense to have some of those addresses not connect to anything. You'd need 19 address line bits to access 0.5 MB, but still 20 bits for a 0.6 MB chip, which would be a waste. Interestingly, it wasn't always so. In the days of 16-bit processors, they used paged memory, where 16 bits referred to a "page" and another 16 bits referred to a location in that 64k page. With the 8086 processor design, addresses above 640k were "reserved" for video memory and other stuff... essentially addresses *could* connect to nothing. Page addresses were on 16 byte boundaries, so the chips could address 64k * 16 = 1 M of memory (much of it reserved). However, the highest page addresses go right up to the last 16 bytes of the 1 M limit but the page could still access the full 64k of addresses above that first byte. I think they called it "Extended Memory". So if you had the physical memory, old 16-bit software could address 640k + 64k-16 bytes. I'm sure hackers found ways to store a little more, like in the video memory. I didn't bother to check sources, hopefully the details are close enough.

According to which observer? And what are the observable or measurable effects? Now I think this is partly wrong. The singularity wouldn't (ever?) be completely inside your future light cone, but it still is completely outside your past light cone. That means that while you still can't observe any events "closer" to the singularity than you are (ie. not any event that has ever happened inside the EH before you crossed it), it can still exist in spacetime outside of your light cone. Some events near the horizon singularity can be considered to have already happened, but they're beyond a coordinate horizon for you. It's not purely in the future... it still exists but is beyond what you can see.* If I'm interpreting the light cones correctly, the location of the singularity would literally escape your observable universe. This next part goes against what I've been told (ie. that you reach the singularity with finite proper time), but I get the sense that your perceived distance to the singularity would grow immensely. It would escape at faster than c, and meanwhile your observable universe would shrink? Or would it be very distorted, with a horizon that is very near in one direction and far in the opposite??? * Edit: However, once inside the EH, events near the EH (behind you) are still within your past light cone. So even though you're inside the EH, the black hole could still potentially be visible in some way (as darkness, or as stuff falling into it). You can't see anything ahead of you (which is now like time), but you can still see "behind" you, including stuff from near the EH which you've since passed! I think... you should be able to see anything that has ever fallen into the BH??? I've rambled about with several contradictory statements, but it seems like what I'm coming around to is that even when you're "inside" a BH, you still can't see what's farther inside it! There would be some kind of distortion of distances and time, but what you could see of the black hole would essentially be like the outside of the BH!

Yep, it's 113. How about:

Is there an example number that I missed? Before you answer!, I noticed I made an error in the equation:

I got...

Do you have an undergraduate degree related to any of those areas?

I don't think this is true. I do think it's incorrect in the diagram, because while gravity pulls on the center of the roll, pulling on the paper doesn't. A downward force through the center of the roll has a moment about the point where the holder is connected to the wall. The greater the downward force through the center of the roll, the harder the roll will press against the wall, making it harder to unravel.

Yes, it's weird. I've been trying to figure this out and I can't. The EH does pass the falling observer at the speed of light. The observer is at rest in its own frame, and the EH (which is traveling at c according to all observers) travels at the local speed of light when it's local (ie. while passing it). The singularity becomes a "time" in your future. Maybe it's counter-productive to consider it being in certain directions. For example say the singularity is like "next tuesday". You could say "anywhere I look, and any direction I go, I will reach next tuesday", but "next tuesday is in all directions" sounds silly. HOWEVER it does seem that depending on which direction you might try to go inside the EH, or perhaps at different locations you might see, next tuesday can come quicker or slower depending on direction. Interpreting light cone diagrams... Source: http://faculty.etsu.edu/gardnerr/planetarium/relat/eventho2.gif It seems from the past light cone at r_S (the event horizon), nothing closer to the singularity is in your past light cone. That seems to imply that anything that crossed the EH before you, cannot be seen in a state after it crossed the EH. I don't know if it would fade away or only be visible in a previous state. I must be reading this wrong???? because if you were following something (or even had your arm out in front of your face), you could not see it cross the EH before you do? It does seem that anything you can see, in any direction, is from events farther than you are from the singularity. That sorta makes sense: The direction of the singularity is "the future" and the every event you can see happened in your past, away from the singularity. But this seems to imply that once you cross the EH, the interior of the black hole can't be seen in any way (not what's in it nor a dark void) because it hasn't happened yet! I'm certain I'm looking at this wrong... But I think you're right... it seems that everything you can see, all around you, would come from "behind" you.

Ah, I see. After I wrote the previous response, I figured I may have misread the thread. So the problem is not that bon needs to *explain* more what the details are or mean, but must *specify* them (in the diagram or maths)?

But... doesn't that light-cone correspond to the local reference frame of the falling observer? The singularity is at some time in the future in any direction the observer points (at different times in different directions). Thanks for the replies... I think I'm speaking from naivety and need to study this a lot more before I'll understand it. Bleh, despite that last statement: The singularity would be approaching from all directions. It would be more like a shrinking Hubble volume of an accelerating universe, in the analogy. But not really... maybe...

I'll try to explain what seems to be the problem: The paper roll is on a rod hanging freely from a string attached to the wall, letting it press against the wall, with some amount of force due to its weight. Depending on how the roll is oriented, pulling on the paper to unroll it will affect the force with which the roll is pressing against the wall. It is hypothesized that this difference in force is the essence of what makes one way easier than the other. So the question is how to determine the force.

I don't think it would work, because the left edge of the graph would be a single point in space, existing in an observer's past, present, and future. That time-like vertical line for an outside observer, would become a space-like horizontal line for an observer approaching the singularity. It would be everywhere in space, and only in the (inside observer's) future. If it's an "edge" of spacetime to the inside observer, it would be an end of time. I don't know what that could mean, or with the analogy, what it means to "reach" the singularity and what happens then. If the analogy makes sense, then an observer could never reach the singularity in its own frame of reference. The inside observer would be at rest in its own frame, traveling through time at 1s/s, toward the singularity (the end of time), which is all throughout space. Edit: Apparently the time to reach the singularity is finite for a free-falling observer, according to GR. This seems to completely break the analogy.

Light-like is a null interval... ie. the surface of a light cone... where the space between two events is equal to c times the time between them. The event horizon, like all vertical lines in the diagrams, are (purely) time-like to the distant observer (whose coordinates are used to plot the diagrams). The EH is light-like to an observer free-falling into the BH, as the EH passes the observer.

If you passed through a BH's event horizon and survived the tidal forces, would the interior seem much like the rest of the universe outside of a BH? - Inside the EH, your future light cone points toward the singularity. This means that in every direction that light can travel, is the singularity. Therefore it appears to be all around you. The singularity looks "as big as" all of space. - Every future light cone very close to the singularity is also pointed toward the singularity, so you can't see it. It looks like blackness at the edge of space, receding from you. Light cones of objects around you also tilt toward the singularity. They all look like they're accelerating toward the singularity???, which is in all directions, so it looks like an inflation of space??? - When you cross rS, the event horizon is a surface that passes you at the speed of light. As you approach the singularity the EH might recede from you faster than the speed of light (read that somewhere, forget where). Might this also appear as the edge of space, receding from you faster than the speed of light? Could it seem to recede into a point on your negative time axis, like a sort of big bang? (I don't think the big bang and CMBR fits this idea.) - Apparently, if you calculate rS for the estimated mass of the universe, it works out to something close to the size of the observable universe (read that somewhere, forget where). So would the analogy only work (if at all) for BHs that immense? Since BHs are inside the universe and part of their mass, would that imply that if a BH is like a universe, you can only fall into smaller BH universes, until you enter one that kills you or ends with you reaching the singularity, perhaps suffering heat death??? This might belong in speculations, but is there any sense in thinking of the EH of a black hole as the edge of space in the past, and the singularity as the edge of space in the future (to an observer inside the EH)? And then reversing the argument could we examine our universe as though it is a black hole? Or are there certain detectable differences that would rule this out? (Shameless speculation: Could the big bang be like all of time passing in the universe that you leave when you cross the EH, in an instant, though it is not seen immediately but instead looks like CMBR? )

I think the lol means: Getting along fine without agreement implies that agreement is not a practical necessity in life. Not needing something doesn't imply that it is wrong. Eg. people disagree with evolution and get along "fine" in other things.

I googled "black hole time cones" to find images of what I was imagining. The following shows how the light cones gradually tip over, and time becomes spacelike. Time is normal to the "spacetime fabric" shown, I think. From http://212.201.48.1/course/fall02/c210101/students/BlackHoles/Black%20holes%20and%20Schwartzschild%20geometry_files/image030.gif The following shows what happens at the event horizon. From http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/black_holes/bh_lightcones_st.gif Not sure if I have this right: At the horizon, time and distance is light-like, to an observer in flat spacetime (at an infinite distance)? Light (if directed outward?), which locally covers distance and time in equal measure, in the distant observer's coordinates passes time without covering any distance. Inside the horizon, all light vectors point toward the singularity, some more directly than others. But they don't point directly at it (horizontal in the diagrams), because... One more complication (and an error in the above diagram) is that the cones get narrower as they get closer to the singularity... From http://faculty.etsu.edu/gardnerr/planetarium/relat/eventho2.gif I don't think the time axis ever becomes horizontal except at the singularity, and the cone becomes thin enough that a light-like path is never horizontal from any distant observer's frame. In other words, no one ever measures calculates light traveling some distance in zero or negative time. So if we say "light seems to be moving slow near the event horizon" we're not talking about the speed of light. The diagrams of cones suggest that to a distant observer (who "sees" a tipped cone), light would not seem to move at the same rate in all directions. Is it only outbound light that seems to be slow, while inbound light seems to move quicker than usual?

I'm not an expert, corrections are appreciated... Before black holes were called that, they were called "frozen stars". While light theoretically travels at c *locally*, that doesn't mean that from our perspective far from a black hole, that the light would be zipping around and back into the BH as fast as light zips around Earth's neighborhood. Near the event horizon, time slows so much that photons (which we can't see because they don't escape to us) would seem to be moving very slowly, even frozen. Yet locally they'd still be traveling at c. The event horizon at the Schwarzschild radius is called a "light-like surface". That means it is moving at the speed of light relative to any observer. As per the name it seems frozen to outside observers. If you fell in to a BH, you'd pass it---or rather it would pass you; since it is light-like there is no valid rest frame of reference there which other things can move relative to---at the speed of light. After rambling I don't know what my point was going to be. Distance and time are so distorted (for lack of a better word) in and around a BH, that you can't get far imagining light behaving as it might in more ordinary spacetime. Geodesics bend back toward the BH, yes but... ...actually this is a question: If light is traveling directly away from a BH, where does its geodesic "point"? Does it point straight back down to the center? From what I understand, light pointing straight out of a BH, from our perspective, would keep traveling outward forever, seeming to us to be "frozen" at the event horizon??? Edit: After thinking about it, I don't think that "light pointed straight out of a BH" even makes sense. Inside the event horizon, it would still move toward the center even if it was aimed directly out.

Look up what free fall actually means, and try to figure out if the device is in free fall or not. This is what I mean by overlooking physics. You're deciding that what you haven't considered, you don't like, and so it can be ignored. It's the same principle that keeps cartoon characters up when they don't yet realize they're supposed to fall, but it doesn't work in the real world. You can explain the behavior of a device in different ways, some easier than others, but it won't behave differently based on how you choose to explain it. Ignoring Newtonian laws doesn't free you from the effects they predict.

On the ground you have the ground holding you up, with an upward force that balances the downward force of gravity (otherwise you would keep accelerating downward). You are correct, you've overlooked something but it's been explained in different ways already. You've overlooked it in the sense of "To ignore deliberately or indulgently; disregard." You're saying that the mechanism that keeps this device up is based on the principle that keeps satellites up. But satellites are in free fall, and you don't like that idea, so you purposefully ignore that "model". If it's not in free fall then by definition it has forces other than gravity acting on it, and you're hand-waving past that by saying "There is something here in these rotating and oscillating Masses." But you're proposing a force with no reactive force, in violation of Newton's laws of motion. You have to show that the mechanism of the device is not confined by those laws, which you can't (cause it don't). You can't just ignore models because you don't like the gist of them. To quote Feynman, "You don't like it, go somewhere else! To another universe! Where the rules are simpler, philosophically more pleasing, more psychologically easy." Otherwise, you must abide by the rules of the universe, or show---not guess---that we've got them wrong. The thing you've overlooked is physics. Sadly, you must work with the models that say that the device doesn't work. You can choose different models but they can't both be correct and give different results. I've tried to explain this in terms of equal and opposite forces, EdEarl has shown that the masses would not accelerate in the direction you expect, and DH has shown that your device is in free fall (unless it disobeys Newton's first law). That's several things you've overlooked. You've overlooked why satellites stay in orbit, what forces actually act on gyroscopes, and how Newton's laws of motion apply.

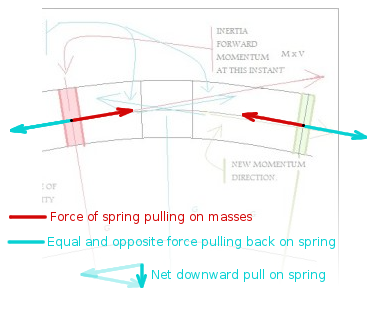
Here's what I mean... This shows the forces the device employs when the spring is fully stretched, when trying to use orbital mechanics to counteract the effects of gravity: Assuming that the spring system is set up to pull the masses back along the same orbital path, then the force exerted back on the spring has a net downward direction. The effects of the force of gravity is already accounted for here in the curve of the orbital path. The spring has to pull the masses relatively *upward*, and the masses are then pulling back relatively *downward*. Surprise!, the effects of gravity remain. Now to be fair, the opposite happens when the spring is fully compressed. It pushes relatively downward on the masses and the masses provide an upward reactive force. However, when the spring is more compressed, the masses are closer together, the force vectors are closer to horizontal on the diagram, and the upward force on the spring when compressed is less than the downward force on the spring when stretched. You can fiddle with the masses and the length of the arc and all that to trick yourself into making the effects of gravity seem to disappear relative to the other forces, but you can't do that in nature. Gravity still contributes the same despite other forces or velocities etc. This isn't the only way to explain why the device won't work, it's just one of many. My point is that if you provide some upward force to counteract gravity, yet disallow an equal and opposite reactive force pushing downward on something, then the device disobeys Newton's third law. Since you're not proposing a "reactionless drive" force here that could speculatively break that law, it won't work.