phyti

KJW; If there are as many even integers n in E as integers in N and if there are as many odd integers n in D as integers in N then there are 2n integers in the union of E and D. Does that seem logical?

pzkpfw;

KJW; 1. To Cantor, his mathematical views were intrinsically linked to their philosophical and theological implications – he identified the Absolute Infinite with God,[57] and he considered his work on transfinite numbers to have been directly communicated to him by God, who had chosen Cantor to reveal them to the world.[1] 2. Let M be the totality (n) of all finite numbers n, and M¢ the totality (2n) of all even numbers 2n. Here it is undeniably correct that M is richer in its entity, than M¢; M contains not only the even numbers, of which M¢ consists, but also the odd numbers M¢¢ . On the other hand it is just as unconditionally correct that the same cardinal number belongs to both the sets M and M¢. Both of these are certain, and neither stands in the way of the other if one heeds the distinction between reality and number.[2] 3. As Leopold Kronecker claimed: "I don't know what predominates in Cantor's theory - philosophy or theology, but I am sure that there is no mathematics there." [3] "Actual infinity does not exist. What we call infinite is only the endless possibility of creating new objects no matter how many exist already" (Poincaré quoted from Kline 1982). [3] Wittgenstein denies Hume's principle, arguing that our concept of number depends essentially on counting. "Where the nonsense starts is with our habit of thinking of a large number as closer to infinity than a small one". reference. [3] 4. Numbers and counting are reality. Functions plot a y corresponding to each x for y=2x. His desire/motivation to sell transfinite numbers seems to have affected his interpretation of the 1 to 1 relation as part of the cardinality of the infinite. A true 1 to 1 correspondence for E=2D. D 1 3 5 7 9 ... E 2 4 6 8 10 ... ----------------------------------------- [1] 'Georg Cantor', Wikipedia [2] Ewald, W., From Kant to Hilbert, Oxford 1996 [3]en.wikipedia.org/wiki, 'Controversy_over_Cantor's_theory'

KJW; KJW;

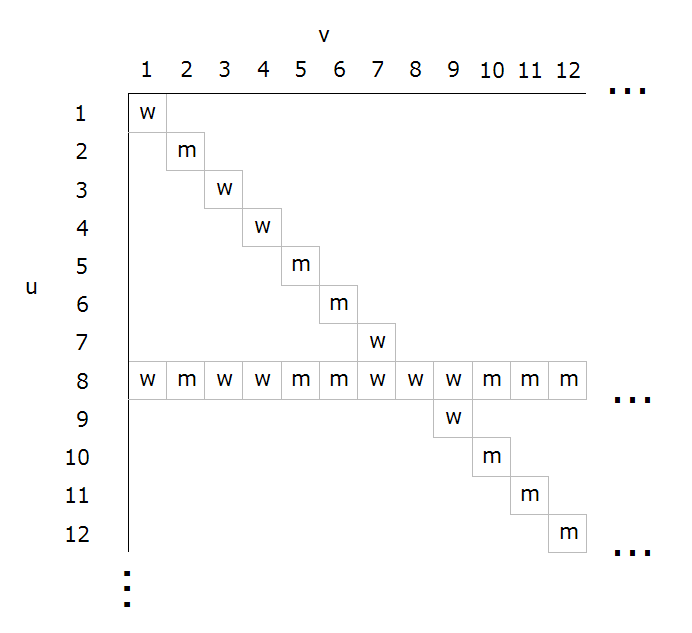
KJW; In his 1891 paper Cantor defined the elements of M as horizontal sequences of m and w. "Let M be the totality [Gesamtheit] of all elements E." Here is the beginning of the list corresponding to M with {0, 1} substituted for {m. w}. 1. 000000... 2. 100000... 3. 110000... 4. 111000... 5. 111100... 6. 111110... ∶ 'Infinity' is not a number, It's a state/property of not having a boundary, thus can't be measured (counted). There are no degrees of infinite. A thing has a boundary or it doesn't. If you know the value of א tell us what it is. In choosing an integer in N as a corresponding identity for a sequence, the list automatically becomes infinite with no last sequence. There is no last integer. For every sequence added to the list, there is another integer n+1. The set N is inexhaustible. The blue symbols represent a different definition of a sequence b that extends in two dimensions, u and v. Each of those symbols is contained in a different E. Cantor never proved b was a new sequence. Notice b is the same as E1.

KJW;

KJW;

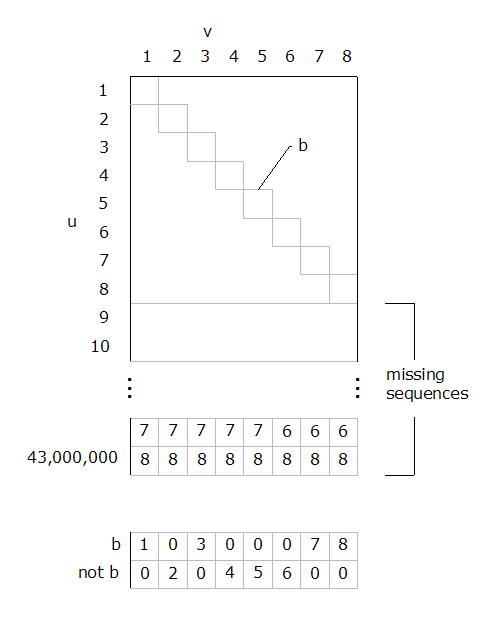
KJW; Don't just repeat what you read. Think about it as if you were doing research. In your 8 column example and all square lists, the diagonal (b) and its complement (not b) cannot coexist in the same square space by definition. That is not a revelation from above. If v=8 columns and the set of symbols is {0 to 8}, then number of sequences/patterns is s=98 = 43,046,721. (Not b) can exist in the missing portion of the list. The list is incomplete!

KJW; That is the power set and not the subject of the 1891 paper analyzed. From the translation: [defines set] "Let M be the totality [Gesamtheit] of all elements E." [defines elements] "EI = (m, m, m, m, … ), EII = (w, w, w, w, … ), EIII = (m, w, m, w, … )." [states cardinality of M is different from N] "I maintain now that such a manifold [Mannigfaltigkeit] M does not have the power of the series 1, 2, 3, …, v, …." [displays M in terms of coordinates (u, v) "For proof, let there be E1 = (a1.1, a1.2, … , a1,v, …) E2 = (a2.1, a2.2, … , a2,v, …) Eu = (au.1, au.2, … , au,v, …)" [defines diagonal b, forms negation as E0] "Then there is a series b1, b2, … bv,…, defined so that bv is also equal to m or w but is different from av,v." He doesn't consider any relation of u to v, which is s = 2v in this case. If the sequences involved 'how many unique patterns can be formed with 5 unique symbols, the relation would be s=5!, i.e. the geometric form depends on the rule of formation. As shown in fig.3, the red diagonal sequence of 64 columns is impossible in a list of sequences 6 characters long, which is true for all v which =n from set N.

KJW; Theories are proposed but only accepted with evidence of experience agreeing with prediction. Mathematical conjectures are no different. Other conjectures have been proven and disproved. Thus I can't agree with accepting math as true without proof no more than some one guilty of a crime without evidence. I have included the paper in png format so you can avoid any risk. The issue is geometric form of the list, a common early objection to cda. His 'contradiction' is essentially a tautology equivalent to 'a thing can't be in two different locations at the same time'. His flawed vision of an infinite list easily qualifies as a contradiction.

KJW;

If we copy Cantor's method, we can expect to get the same results. That does not prove his concept of transfinite sets is correct, only consistent. The new analysis begins with an early objection regarding the geometric form of Cantor's list. Does the progression of finite lists lead to transfinite lists? Cantor's Illusion.pdfCantor's Illusion.pdf

KJW; Let's assume Cantor is correct about the missing E0. The purpose is to explore the results of his conclusion. There are many possible random lists with different orderings of sequences. Consider forming a finite list of 5 different sequences (abbrev. s). There are 5 s for line 1, 4 s for line 2, ..., 2 s for line4, and 1s for line 5. There are 5!=120 different lists. The content of each list is constant, with only a different order. I.e. there are more lists than sequences. If Cantor applies his diagonal method to each list, the number of missing sequences > the number of sequences! That qualifies as a contradiction.

; Let's assume Cantor is correct about the missing E0. There are many possible random lists with different orderings of sequences. Eg. swapping the 1st k sequences with k randomly selected from other parts of the list. Thus, the number of lists > the number of sequences. Cantor forms a diagonal d and its negation E0, beginning with sequence 1. of a random list L1. Rename E0 as x1. Cantor forms a diagonal d and its negation E0, beginning with sequence 1. of a different list L2. Rename E0 as x2. Cantor forms a diagonal d and its negation E0, beginning with sequence 1. of a different list L3. Rename E0 as x3. Continuing to apply Cantor's method, there is a missing sequence x for every list. Thus the number of missing sequences > the number of sequences!

LIGO detects gravitational waves, since 2016. Gravitational waves are very low frequencies < 7000 Hz, well below the visible range. Thus the waves are detectable while the black hole is not visible. The statement ‘even light can’t escape’ is referring to the range detectable by humans. Pound-Rebka did an experiment demonstrating light (em radiation) gains energy moving in the direction of a g-field, and loses energy moving in the opposite direction. This is in agreement with gravitational red shift.

If light cannot escape a black hole, how can gravitational effects radiate into space at light speed?

Jeff; The A-list is the conventional form for a list, one sequence per line or row. Cantor defined a different form D using the diagonal elements, one character from each sequence, from the A-list which becomes the unconventional form, the B-list. The blue characters in the A-list do not represent a sequence in that list, and he does not alter the A-list. He then forms E0 the negation of D, overlays it on the A-list as a horizontal sequence, and states it would conflict with D, if D was literally in the A-list. He sees what he wants to see to prove his point, that the A-list is missing E0. He ignores the fact; if E0 is missing, so is D, they exist in pairs as shown in the B-list. In the conventional A-list all sequences are randomly formed and entered randomly. Since they are all parallel, there is no interference of one with another, a property of random lists. Yet when Cantor mixes the diagonal with the horizontal sequences, it imposes restrictions on the locations, a form of order where there should be no order! His goal, Cantor states M has a different cardinality than N the integers. "I maintain now that such a manifold [Mannigfaltigkeit] M does not have the power of the series 1, 2, 3, …, v, …." Cantor would be wasting his time demonstrating a subset M1 has fewer elements than the set M, when it does so by definition. The 'ordered set of characters' is the order they have within a sequence. Ignoring the orientation, they appear the same, but they differ, and that is the problem. If you think E0 cannot exist as u83 in the A-list, explain why. Cantor fooled himself first then many others. It's the illusionist's form of misdirection, 'look over there (while I do something over here)'.

My disagreement is with Cantor's diagonal argument, his method of proving his transfinite/infinite set M has a greater cardinality than N the natural/counting integers. It doesn't depend on any class of numbers. It is based on Cantor's own writings. Enclosed is a revision of the analysis. Cantor's illusion.pdf

; Cantor shows an example of 3 E-sequences. E1=(m, m, m, m, ...) E2=(w, w, w, w, ...) E3=(m, w, m, w, ...) ... Cantor then assigns a (row, column) coordinate system (u,v) to the array of E-sequences. The character at (1, 1) is an element of E1 The character at (2, 2) is an element of E2 The character at (3, 3) is an element of E3 ... Cantor then defines E0=(b1, b2, b3, ..) where bn is the negation of the same coordinates already assigned to the array of E-sequences. The trivial conclusion, the diagonal coordinates (v,v) cannot be both m and w simultaneously. His contradiction, that a thing cannot be in two mutually exclusive states simultaneously is true. A thing can't be in two different places at the same time. The contradiction is his own creation, by manipulation of a sequence that excludes (prevents) the appearance of others. It’s not an error or inability that causes any sequence to be missing. --------------------------- Since the array of E-sequences is random, there are at least as many arrays/configurations as sequences. For the example there are 6, (123, 231, 312, ...). Applying the cda method to each would mean more sequences are missing than there are existing! There is also the vertical argument, where a random column V is selected, and each character is swapped for its negation. This forms V0 which differs from every E where they intersect. In this case there are as many V0's as sequences, resulting in no array!

wtf;

wtf; Your reference to algorithms opens up other points to ponder. Cantor considers the diagonal formed from one character from each row with coordinates (v, v) a sequence. His method of formation for E0 is to swap characters m and w. He doesn't specify a method of formation for the E elements in the list/array prior to E0. It can't be the same since the first E would have nothing to modify. The diagonal cannot be completed until the list is complete. If the list is complete, E0 is redundant as a duplicate. As Wittgenstein noted, the product of an algorithm/procedure is not without limits/infinite, it's the algorithm/procedure. For the integers of N, a unit can be pulled out of nowhere, added to any current integer to form a larger one. As stated by one mathematician, 'mathematics' is a manipulation of symbols (total abstraction). As for a program to generate the set N: 1. x=0 2. n=x 3. x=n+1 4. if x>n, goto 1 ;n is not the greatest integer 5. stop n+1>n = 1>0, which is always true, thus step 5 is redundant, and never happens. Any process requiring an infinite number of steps, never reaches its goal.

Jeff; He doesn't have to use the word 'diagonal' when that is what he describes. If Cantor uses 2-dimensional coordinates, he is using geometry, whether you recognize it or not. Cantor showed a partial list because that's all he had. There is no complete list. He is asking the reader to imagine of pretend it exists. Consider N the natural/counting integers. There is no greatest integer, thus no one will ever see a complete list of N. A complete list of an infinite set is a contradiction of terms. It is always incomplete, since there is no last term. Which brings us to the real world of finiteness. Objects have boundaries which allow measurement. A sequence (ordered set of elements) can be modeled as a rod of constant cross section with a definite length x. To measure x, the zero end of a tape is fixed at the near end, and x = the nearest mark on the tape that coincides with the far end. For astronomical distances light is a better method. An emitter is fixed at the near end of the 'infinite' (latin for 'no boundary') sequence/rod. Where is the far end with a reflector? There is none, and that is why 'infinite' also means immeasurable. The methods of measurement were developed for applications in a world of finite objects. They don't work for objects without boundaries. Then there is empty. A container can be empty, but it can't be emptier. There is no superlative degree of empty. There is no superlative degree of infinite. It's a state/condition of unlimited extent. 'Infinity' is not a number. Jeff; I'll leave you with this graphic which you ignored previously. It's the primary proof that Cantor's construction of the diagonal D is not new but a duplicate of an existing sequence/string/(your favorite word). This is the list using his characters/symbols, without the E's and the remaining sequences. The focus is on D beginning at u1 and its duplicate as u8. There is nothing to prevent u8 from appearing in the list before Cantor alters it. It's a random list of all possible sequences, each independent of the others. The sequence of m or w could be decided by flipping a coin (H or T). A random list has no order, contrary to Cantor's philosophical rambling on 'well ordered' or 'determinate' sets. If m precedes w as a rule of order, the 1st row u1 would be all m's. The 2nd row u2 would be the same except a w in the last position, but there is no last position! His method has no provision for detection of duplicates, which requires a comparison of all symbols beyond the intersection at (8, 8). If D is not new than neither is E0, the complement/negation of D. Each row/u can correspond to an integer from the set N, which also has no end. He like everyone else, had no experience with things that are endless or boundless or infinite, thus no ability to conceptualize his idea.

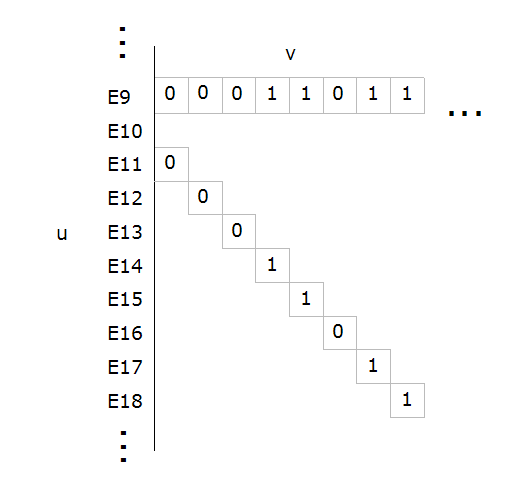
Jeff; I only read what Cantor wrote. Your interpetation is distorted. Cantor used the 2-dimensional coordinate system, u for row and v for column. The letter s will stand for sequence/string. The symbols 0 and 1 have coordinates (u,v). For the horizontal s, u is constant equal to 9 and v varies as (1, 2, 3, ...). For the diagonal s, u varies as (11, 12, 13, ...) and v varies as (1, 2, 3, ...). They are different things with different properties. A case of basic geometry.

; It's not about numbers, real, imaginary, or otherwise. It's not about surjection, injection, objection, or any similar forms. It's definitely not about subsets. By definition they contain less elements than their set of origin. That doesn't require a proof. Anyone who thinks Cantor was describing subsets, questions Cantor's abilities. From reading his philosophy paper on set theory: He is considering a heirarchy of infinite sets, each as a complete independent thing. As an abstract concept in the field of pure mathematics, they do not require any type of physical correspondence. I have never seen anyone state a list is the same as the set M. A list is only a visual aid for the purpose of understanding. Cantor nor anyone else has such a list. He shows a sample of an incomplete list of incomplete sequences. That's why the ellipsis ... was invented, to project a thought and move on. My issue is more about logic than anything else. To paraphrase Cantor (substituting for m & w) "Set M contains all possible infinite sequences {E1, E2, E3, ...} composed of 0's and 1's." and before he defines his diagonal "the set M does not have the 'power' (cardinality) of N the natural numbers." thus no one to one correspondence. The set M can be divided into 2 subsets, M0 and M1 M0 0000... 0101... 0011... 0110... D=0110... E0=1001... Cantor declares E0 is not in M. It is a sequence but can't be in the list. It can't be a member and not a member. error 1. It's a sequence of 0's and 1's, but oriented at 45º to the horizontal sequences, thus it intersects all horizontal sequences, where no other sequence does so, the points of intersection only allow one symbol, so E0 is excluded from the list by the introduction of the diagonal. Before the diagonal, the sequences are independent of each other. error 2. The standard convention for the printed page is horizontal rows of text, extending vertically in a 2 dimensional format. A diagonal row of characters would have no meaning relative to the context of the page. error 3. For whatever reason, he made his own contradiction, by not recognizing the complementary properties of binary sequences. If a sequence has each symbol swapped for the other, it becomes the complement of the first, i.e. they exist in pairs. This is evident if M1 is compared side by side with M0. E0 (blue) is a member of M1. E0 being a member of M1 and not a member of M0 is not a contradiction. Also note in M0, the 4th sequence is a duplicate of the diagonal. Cantor could not detect it unless he compared every position after the intersection! With the introduction of a single diagonal sequence, Cantor presented a self fulfilling prophecy. That would be appropriate, since he claimed his idea had a divine origin. M1 1111... 1010... 1100... 1001...