slick
Members-
Posts
12 -
Joined
-
Last visited
slick's Achievements

Quark (2/13)
0
Reputation
-
Not sure what that means, surely any problem that has hung around as long as this one needs a 'wrong' approach since all of the 'right' approaches have been fruitless (with the obvious exception of Andrew Wiles' solution whose own approach was to prove an apparently unrelated conjecture). BTW: Are you saying that my solution is wrong?
-
Hi Tony, let me try to explain a bit better, it was very late last night and I didn't really flesh it out properly. The shaded area of my diagram illustrates triangles that, for any value of c (c being the bottom line), would have an angle C >= 60o and < 90o. This is because it is self evident that any other values of a, b and c that do not result in a triangle angle C >= 60o and < 90o cannot produce the result an + bn = cn. For values of a, b and c that do result in the described triangles, increments of n will cause the angle C to widen until it passes through 180o. Up until it passes through 180o an + bn will still be greater than cn however once it has passed through 180o an + bn will always be less than cn. The question then is whether, for any increment of n, angle C can ever be exactly 180o since that would mean that an + bn = cn. It would also be true at that point that the area of the triangle would be zero. This is, of course, what happens when you start with a right angled triangle and square the numbers. My objective therefore is to find a way to determine if any triangle with an angle C >= 60o and < 90o can ever have zero area and/or an angle C of 180o for increments of n and to determine that I took a portion of my triangle around the angle C that equates to c' = 1, b' = 1 and a' = whatever results from joining c' to a'. Now for any increments of n b' will always remain 1, c' will always remain1 and a' may increase or reduce. For any circumstance a' can never be zero and it is only if a' becomes zero that the triangle can have zero area with angle C = 180o. Since that portion of the triangle can never have an area of zero it follows that the whole triangle can never have an area of zero consequently an + bn = cn cannot be true for n > 2.
-
I think I understand what you are saying however it is always worth clarifying. To my mind you seem to be saying that for any 3 integers a, b and c where a + b = c, for there to be any common root > 2 at least one of a b or c must be irrational. If I have understood correctly then I think that is highly probable however it doesn't seem fundamentally different to the original problem, just a re-statement in reverse. It may be worth looking at the Golden Ratio to see whether there is any relationship there.
-
slick started following Fermat's last theorem
-
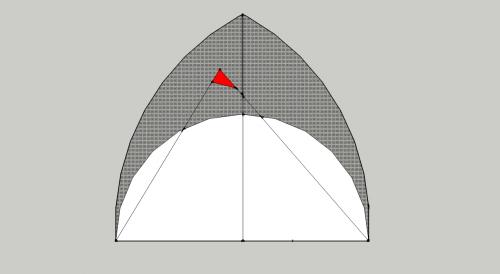
Okay, here is an attempt at a simple proof. I said before that my primary concern is with positive integer values of a, b and c that can form a triangle with an angle C < 90o and >= 60o. What I realised fairly early on was that for an + bn = cn the resulting area of the triangle would have to be zero. My thought then is to take a portion of the triangle such that both b' and c' are both 1 which would mean that for that portion of the triangle to have zero area a'n would have to result in zero. The picture below shows what I mean. There are, of course, no circumstances in which a'n can equal zero therefore the whole triangle can never itself have an area of zero. The only exception to this is for a right angled triangle since in those circumstances a'n would always be zero. I await your brickbats!
-
How does that relate to The Tree saying - "There are definitely no rational solutions to an+1=cn, it's a fairly trivial special case." Can The Tree elaborate on that. Nor am I trying to. My interest is in why such a simple looking problem is so difficult and to do that I am trying to understand where the actual problem lies. In other words, what is the point at which anybody attempting to resolve this realises they have hit an obstacle that cannot be overcome? I should declare that it is a professional interest for a business solutions methodology I a working on for which I am using FLT as an unambiguous reference case.
-
Thanks but do you think that it can also be true for a and c being positive rational numbers?
-
TonyMcC, I was thinking about irrational numbers last night. One of the things that occurred to me while messing about with triangles, although it may be incorrect, is that I could reduce the scale down such that either a or b are equal to 1 which would mean that an + 1 cannot = cn where a and c are rational numbers and n is an integer > 2. In other words, take any rational number and subtract 1. For any root of the first number, the resulting root of the second number must be irrational however I don't know enough to be able to test whether or not this is true.
-
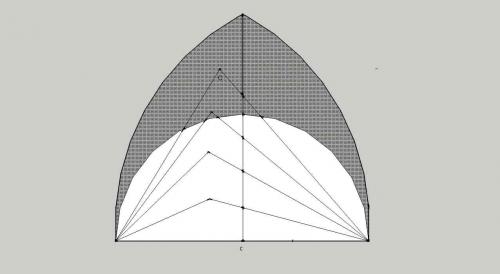
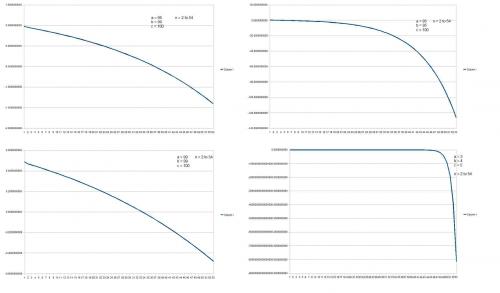
Happy new year! I have been having a bit of fun with this over the holiday break and I am getting nowhere quite slowly. My lack of knowledge seems to be a bit of a stumbling block for some reason but it has been fun re-learning basic trig so I thought I would give an update on where I have got to. My conclusions so far are that there is only one scenario that is problematic: where a2 + b2 > c2 and neither a nor b are greater than or equal to c. For the other scenarios such as a2 + b2 = c2 ora2 + b2 < c2 or where either a or b are greater or equal to c then it is quite easy to see that an + bn cannot = cn. I concluded that the difficult scenario could be represented as any triangle of three integers where the apex of a and b is in the shaded area in the picture below. This is any triangle with an angle C between 60o and 90o. I then started endless messing about with the area of the triangle (which would have to be 0 for a positive result), the height of the triangle (which would also have to be 0), the angle C (which would have to be 180o) and various other permutations. The area/height option looked promising since zero is such a good target but I couldn't really find any other way to predict the expansion/contraction other than by standard equations and there would be little point proving that the area can only be zero if an + bn = cn, it kind of gets things the wrong way round. So now I am looking at the basic equation a2n + b2n - c2n / 2ab which must equal -1 for a positive result. What I have seen is the progressive value of the result is an arc (not surprising) which passes through -1 but I cannot see yet how I can determine why it will never equal -1. The four graphs below show the progression of the result for n = 2 to 54 for four sets of values. I am also finding it difficult to get good results since my laptop seems to run out of computing ability once I get past n = 50 for values such as 99,99,100 for which I have yet to get to -1. What I think I really need now is a different way to calculate the expansion/contraction of the area of the triangle. Any suggestions?
-
It will take me a while to fully understand your posts but thanks for pointing me to them, there seems to be some resonance to what I have described. Specifically I can conclude from my description that if a, b and c cannot form a triangle then either a2 + b2 must be less than c2 or a or b must be greater than c. In either case I can demonstrate FLT. If a triangle can be formed then for all triangles where the angle opposite c is less than 60o or greater/equal to 90o then I can demonstrate FLT. I will try to see how this relates to your curves.
-
Many thanks for the input and advice. I have no intention of becoming hooked and I certainly didn't spend sleepless hours in bed last night thinking about it! Okay, so I feel that I can describe this problem for instances where a2 + b2 < c2 ora2 + b2 = c2. The problem, as I see it, comes with a2 + b2 > c2. Within that, if either a or b is greater than c then I can still describe the solution since c2 will fit into either a2 or b2,therefore the problem comes specifically with a2 + b2 > c2 and neither a nor b is greater than c. In triangular terms, that would be any triangle where the angle opposite c is less than 90o but greater than 60o. Some examples: 3n + 4n = 5n is okay since 32 + 42 = 52. 3n + 4n = 6n is also okay since 32 + 42 < 62. 10n + 5n = 8n is okay since 102 is greater than 82. 8n + 9n = 10n is where the problem starts since 82 + 92 > 102. Does this make sense? Is there any value in reducing the problem or is this a well worn path?
-
I was thinking about it last night and realised that there is a more fundamental problem since my third description - "For instances where a2 + b2 > c2 then I don't even need to describe squares since if the area of a and b exceed the area of c then the cube of a and b combined must be larger than the volume of c cubed." is complete nonsense. As regards "The numbers a, b, c, and n have to be positive integers." - I don't see that as a problem unless you have to allow for negative values of n. In other words, my understanding was that n had to be greater than 2, is that incorrect?
-
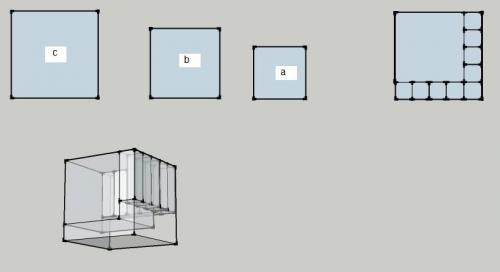
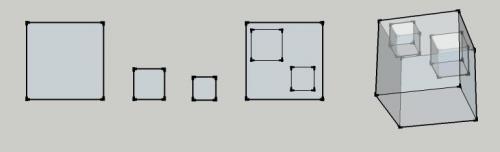
I am a latecomer to this problem having watched the program about FLT and Andrew Wiles and I am no mathematician so I am looking for a bit of help understanding this. I have googled and read but most of the stuff is completely impenetrable for a layman. The thing that confuses me most is that the theorem seems fairly easy to 'prove' in descriptive visualisation terms so why is it so difficult to prove mathematically. How I visualise it is as follows: The basic premise is: an + bn = cn cannot be true where n is greater than 2. My starting point is to visualise pythagorean triples where a2 + b2 = c2 is true. In this case I can describe three squares of which square a and square b will exactly fit into square c. If I now cube a, b and c I can see that although one face will be an exact fit the total volume of a and b must be less than the volume of c. Notch it up to a4 + b4 = c4 and the differential can only get larger since I will now have c times as many large cubes but only a times as many a cubes and b times as many b cubes. Since n is incremental the differential can only get incrementally larger. For instances where a2 + b2 < c2 then again I can describe three squares, two of which (a and b will fit into c with some remainder. If I now cube a, b and c I can see that the cubes a and b will not only fit into one face of cube c but also then cannot reach or exceed the other faces of cube c. As before, since n is incremental, the volume of c can only get incrementally larger than the total volumes of a and b. Another picture shows what I mean For instances where a2 + b2 > c2 then I don't even need to describe squares since if the area of a and b exceed the area of c then the cube of a and b combined must be larger than the volume of c cubed. Again, since n is incremental, the volume of a and b will grow incrementally larger than the volume of c. So, my questions: What have I misunderstood about Fermat's last theorem? What have I missed in my description? If my descriptions are correct why is it difficult to represent mathematically?