ed84c

So your suggesting I put (M - k I) to the power of T? And then take into account that; -M = M^t and I = I^t?

I cant see how to use that? btw it should look like that

M = -M^t where M is 3*3 prove that det(M - kI) = -det(M+kI) Ok for starters its a square matrix => M^t = M => M = -M for our matrix So to get to our proof my solution would be; det(M) = det(-M) det(M)(I-kM^-1) = det(M)(I-kM^-1) det(M - k I) = det(-M + k I) Unfortunately as you can see this doesn't give the answer... any ideas?

The first line of working should = 0. This has something to do with cyclic interchanges but I dont think that is relevent and probaby just confused things by mentioning it.

Ok sorry. So what I'm doing is multiplying the elements of the second column by the co-factors of the first column- this the same as doing a cyclic interchange of the columns which we know from the rules of matricies = 0. So what I've done is multiply the second column (b's) by the cofactor of the first column (A) yielding the second line of my original post. However we need to make sure that we attatch the correct signs to each minor (i.e. what is shown in the middle line of my last post) to yield the correct cofactor which is what I have shown in the bottom of my last post. OK I a cyclic interchange leaves the determinant unchanged so ignore that bit. And also A_1 should be the determinant of the matrix I've shown not just the matrix.

With a 3*3 matrix you have; [math] \left( \begin{array}{ccc} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array} \right) [/math] then [math] A_1 =\left( \begin{array}{ccc} b_{2} & c_{2} \\ b_{3} & c_{3} \\ \end{array} \right) [/math] i.e with a_1 row and column removed. Remember you need to introduce the signs; [math] \left( \begin{array}{ccc} + & - & +\\ - & + & - \\ + & - & + \end{array} \right) [/math]

This shouldn't be too dfficult I need to prove (e.g.) ; [math] b_1A_1 + b_2A_2 + b_3A_3 = 0 [/math] Ive managed to get; [math] a_1a_3b_2 + a_1a_2b_3 - a_2a_3b_1 + a_2b_3a_1 - a_3a_1b_2 +a_3a_2b_1 [/math] which nicely cancels out with the exception of 2 terms; giving; [math] 2a_1a_2b_3 [/math] Can anybody see where I've gone wrong?

OK i did it like that but it came out around 10?

at 0.3 its 0.2 away. And no I didnt drop the x; that was the question. Maybe Im doing it the wrong way? This is only the first exersize in the chapter which does not go into taylor series'.

Question: Find a Maclaurin approximation to calculate [math] \frac{1}{\sqrt{e}} [/math] so I go for the M.A of [math] {e}^{-0.5x} [/math] which I have worked out to be [math] 1-0.5x+\frac{x^2}{2!}-\frac{0.5x^3}{3!}+\frac{x^4}{4!}-\frac{0.5x^5}{5!} [/math] But If I now dow f(1) it does not approximate [math] {e}^{-0.5x} [/math] (although it does around f(0)) Any help?

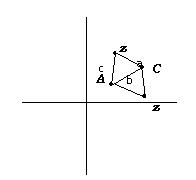
Ok so I have 2 points A = 2 + 3j C = 4 + 7j on our argand diagram they make an equailateral triangle with a point (or more precisely either of 2 points) which I'll call z Now I know; [math] ABC = arg ( \lambda ) = arg (\frac{a - b}{c-b}) [/math] so [math] arg(\lambda) = \frac{\pi}{3} [/math] and [math] \lambda = \frac{a-b}{c-b} [/math] [math] \lambda = \frac{(z-(4+7j))-((4+7j)-(2+3j))}{(z-(2+3j))-((4+7j)-(2+3j))} [/math] [math] \lambda = \frac{z-6-11j}{z-4-j} [/math] No where do I go from here; solve simultaneously, or am I using the completely wrong method? I've attatched a sketch of the argand diagram.

Yep, that checks out. Cheers for that.

Ok so I need to solve; [math] z^{5} + x^{4} + z^{3}+z^{2}+z + 1 = 0 [/math] My first thought is to use the summation equation where a = 1, i.e.; [math] \frac {1-z^5}{1-z} = 0 [/math] but then I'm not sure where to go from there; in the past I have had something^something else = 1 then something = alpha and then made z = f(alpha) however here there isnt a whole term to the same index. Any ideas?

Theres a straight line (l) and a polar co-ord of a point A (p, alpha). The straight line passes through A and is perpendicular to OA. Ive got to prove rcos(theta - alpha) = p Any ideas where to start with this. I've got y = tan(alpha)x for OA.

Cheers for the help, it worked.

Hi Guys, Just started teaching myself FP2 from home so I might end up with a lot of these.... anyway im trying to integrate sin5xcos2x dx but am running out of ideas. Ive tried to get everything into 2x's but each time I end up with something wierd. Any ideas?

How come XP wont boot from USB?

OK so those who followed my last thread will know windows has decided to try and digest itself. After talking to YT I have decided to try and parallel run Ubuntu and XP, but this time from a pendrive, as it should be "apparently" a 300% faster boot time. Now lets assume I can boot from a usb device for the time being, anybody tried this? things I need to consider? I reckon a 4Gb pendrive should do the job (XP is 1.5 Gb and Ubuntu is ~ 1 Gb ?), but what about things like cooling? I think I could build a box for it with a fan from an ABS box and take off the little plastic cover. Anyawy any thoughts would be great. From googling I have seen this has been tried but not sure if anybody has it 100% working

hmmm well. Nothing has changed by me as far as i recall. Just check disk came up once decided to check integrity et al. Then it proceeded to "Repalce invalid security ID XXXX with default one" where XXXX is upto 150,000 at which point i got bored and reset. According to microsoft; when you copy a lot of data this may occur. I just reloaded all songs onto my mp3 player ~ 20 GB so that may have had an effect. Also I have not much disk space. Maybe that has an effect. Either way it looks like from your posts ill have to re-install windows. I *just* have enough functionality to keep revising, so ill do it after exams. Cheers for the help anyway.

Klaynos will enjoy that. However I am now stuck with a problem, thankfully my impatience stopped windows short of destroying everything. Basically it decided all the security id's were wrong and went about setting them to default values in the check disk deely while it boots. Ive googled it, and there are fixes to prevent windows doing it again but not to cycle back all the security ids. Now there is no start menu i have to use task manager to switch between windows, and i cant copy and paste anything or listen to anything (the sound card(s) doesnt exist anymore aparantly). Any ideas to solve this? (Other than formatting and installing linux; I WILL get round to that, but not in the middle of exams ty)

The dangers of nuclear power

Black body radiation I believe. That and/ or the photo-electric effect. Look up both those ideas, should be a good start.

Basic (i.e. Polynomial) differentiation is mid way through the first year. Chain, Quotient, Product rules are all at the begging of the second year.

ah thanks for that. I wondered why he never spoke and didnt look much like elton john.

ah thanks for that. I wonder why he never spoke.