Schrödinger's hat
Senior Members-
Posts
752 -
Joined
-
Last visited
Everything posted by Schrödinger's hat
-

Composing unilateral phase detractors
Schrödinger's hat replied to Cap'n Refsmmat's topic in The Lounge
Before removing the Albertson flange from your heliocentric girdle regulator, you should check the Gaussian metric on the lorentz spacer. The service manual gives a five-gram tolerance for the collimation of the T-pulses, but that doesn't take into account hemostatic vibrulation. Try and reduce it a bit further; sometimes double shimming the rocker-cams can do the trick. Many people will get by relying on the type unifier, but your pearson's correlation coefficients can drift if you're not careful. Best to do it properly now rather than forking out extra money later. -

An Interview with Cap'n Refsmmat
Schrödinger's hat replied to Cap'n Refsmmat's topic in Forum Announcements
Not at all. Although you may have a more trouble getting anyone to publish it or take it seriously if you do not. However, you should not confuse this for people not taking your work seriously because it is not up to the same standard as that of people with degrees. There are certain conventions, knowledge of the language used, and of results in the field that you should be comfortable with/should be apparent in your work. These will make it a lot easier for others to understand it (and thus make them more likely to consider it). -
Yes, for invariant mass and invariant energy. This quantity does not change with velocity. Total energy: E = \gamma mc^2 Or kinetic energy: KE = (\gamma - 1) mc^2 Where gamma is the lorentz factor do. Erm, acceleration is proportional to force. The more mass, the less acceleration (for a given force). The larger an object's velocity, the more energy it has in a given reference frame. But if it accelerated then the energy came from somewhere (such as potential). Yeah, close enough. I think you mean accelerating. The rate of acceleration is changing, but if you're talking about the change in speed, then the concept you want is acceleration -- not change in acceleration. Umm It's hard to tell exactly what you mean. Very loosely, and without getting into general relativity because I don't understand it nearly well enough to explain. The reason bound systems stay together is that there is a force keeping them together (which overcomes the acceleration so that the distance between their components remains constant Let's say I have some large, but light object (so I can ignore that object's gravity for now) that I bound by the electromagnetic force. If I'm in a rocket with the engine turned off, and not interacting gravitationally or electromagnetically with what's nearby (ie. I'm not accelerating), then I will measure any given part of that object to be accelerating towards the object's centre (and measure the whole object to be accelerating away from me). I don't really want to/aren't really qualified get into gravitationally bound systems and space curvature, but you can think of gravitationally bound systems in the same way. This is quite wrong, but it's not so far wrong that it's completely useless. So I guess you are right in a sense. Bound systems are imploding -- but just enough so that they remain a constant size/shape. While 'space exploding' is a useful two word metaphor, but it is only a metaphor. Really it's: On a large scale, spacetime is curved such that the distance between any two objects not accelerating in their own frames of reference will increase with time. On a local scale, curvature can be different. Such as in gravitationally bound systems.
-
Hmm, perhaps I forgot the sarcasm tags. :/
-
Even an estimate is enough to know if the assumption is any good (ie. is it bigger than the barrel? what would be the estimate for the ratio of its radius to the barrel radius, and length to barrel length?)
-

semiconductors from stone knives and bear skins
Schrödinger's hat replied to hombre's topic in Engineering
Sounds like a massive energy sink. -

MIT's trillion frames per second light-tracking camera
Schrödinger's hat replied to Shadow's topic in Science News
If you dig through their site a bit you'll see that it's not actually saving a trillion frames per second, it's compiling trillionth of second snapshots together over a much longer time. They had a few videos which looked like they 'ran' for a few nanoseconds each. Also, things that you're interested in which happen that quickly generally don't happen for very long, so a microsecond or so for each video is probably enough. -
Apologies, I misread 115 as 105 somehow. As Dr Rocket said, this extrapolation is based on some assumptions. Namely: Distance linear with launch energy, which only holds with no air resistance and, Launch energy linear with pressure, which only holds with some questionable assumptions about the gas reservoir. You also haven't really told us what you wanted this for. If you just wanted a ball-park 'about there' and then adjust once you are in the field, then I'd go with my earlier (rather lazy) approach. If you want to understand how and why it went that far, then going into more detail is a good idea. Indeed. As you said, the assumption about the amount of gas available needs to be validated/replaced before this is useful. A simple way of checking how significant aerodynamic effects are would be to compare the kinetic energy of the potato to an estimate of the air resistance force at launch velocity * distance travelled If this number is small then it can reasonably safely be ignored. Else it should be included in the model.
-

The Black Hole at The Center of The Universe
Schrödinger's hat replied to astrocat5's topic in Speculations
And the clocks are only synchronised enough to work because of general relativity. -
No death vibrator. Just a breeze -- and a strong resonance. Energy kept getting fed in, but didn't leave.
-
The geometry of space can alter pi in that space. As insane alien said, 3.14159... is pi in euclidean space. Our space is not globally euclidean. If you were to draw a big enough circle in a gravitational field, you'd notice the ratio between its circumference and diameter was a tiiiny bit different. Our space is locally euclidean¹, so for a small enough circle you get 3.14159.... We use the euclidean pi in our mathematics, so curvature of space cannot change this. ¹Possible exception of singularities -- if they exist. I do not know if they'd count as locally euclidean.
-
You appear to have answered your own question
-
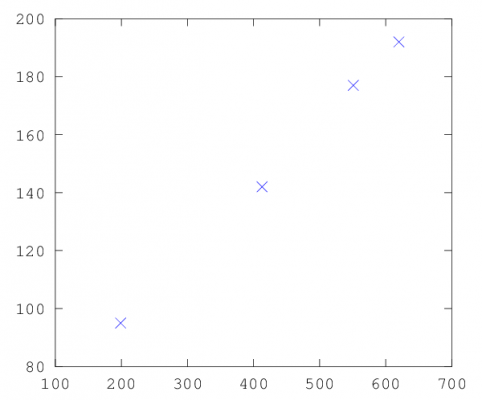
That's not a lot of info to go on. From this data I can't tell if you'd be limited by energy stored (in which case force goes down significantly as the potato moved down the barrel), or more in the domain of constant force, or somewhere in between. How big is the reservoir? Getting into the theory, the distance will be roughly proportional to the initial energy (wiki if you want derivation) Now the initial energy is either going to be proportional to the pressure (in the limiting case where you have an infinite reservoir of pressure), ie. P\propto F and F\times distance = energy.(distance down the barrel is constant) In which case you want to extrapolate linearly. In the limiting case where you have no excess gas (it reaches 1 atmosphere before ejecting the potato) your energy will instead be proportional to the log of the pressure. A quick plot of the data seems to indicate that it's roughly linear (although over a small enough range that a log plot doesn't look much different). Graph of distance in metres vs pressure in kPa Acting on an assumption of linearity, a quick mental calculation yields 680 feet for 100psi, and 700 for 115. If you care about getting more precision and some error bounds (assuming the linearity assumption of linearity holds), then a linear regression would be a good idea. Without more data, it's hard to tell how accurate this model is. The only thing I can think of if you can't take more data is to do the calculations from the pressures (maybe including air resistance or an approximation thereof), and see if those distances pop out. It would help to know exactly why you wanted to know this and whether or not you could take any more data. The constant pressure assumption would also need to be justified (what is the volume of the section of the gun which the potato does not pass through?)
-

Whack degenerate matter with a baseball bat
Schrödinger's hat replied to Toadie's topic in Classical Physics
The difference is the deep (and steep) potential they are in. Change the gravity (by changing the totall amount) and you can't say that the previously stable state will stay stable. (Similarly I cannot say without doing the sums that it will be unstable, but I know there is a point somewhere between a neutron and a stellar mass ball of neutrons that it becomes unsstable) I would call burning off quickly an unstable state, but regardless, when it comes to having an event horizon things are a bit different. I can't quite follow what you said in that last bit, but I think it may be the same line of logic I was using. -
You'd fit in well in Ancient Greece Spacetime is locally euclidean, so you can always get the same 3.141.... number by drawing smaller and smaller circles and seeing what values you get for the ratio of the circumference and diameter. Unless your circle included a singularity, in which case you'd have a bit of difficulty measuring the radius.
-

Whack degenerate matter with a baseball bat
Schrödinger's hat replied to Toadie's topic in Classical Physics
I think mathematic's point was that the phrase 'degenerate matter on earth' implies a much smaller quantity than the stellar-mass sized chunks we observe in nature. If it were a white dwarf or neutron star, the phrase would be 'earth in degenerate matter'. If we extend this logic to arbitrarily small chunks of neutron-degenerate matter, all nuclei are stable. Thus there is a tipping point where (at least for neutron-degenerate matter) it is unstable. Iit is impossible to know where this line is without modelling the relevant equations for a small amount of mass, Or doing some kind of experiment. However, I'd wager that it'd be closer to the mass of a planet than the mass of a mountain. Similarly the logic of: It is in this state, therefore it is stable. Does not hold for electron degenerate matter. -

Mirror test of self awareness
Schrödinger's hat replied to Greg Boyles's topic in Anatomy, Physiology and Neuroscience
I always interpreted such tests as being considered sufficient but not necessary. If a crow uses its reflection to locate a piece of tape on one of its feathers, or an ape uses it to remove a smudge on its face then we know the animal realises the reflection is themselves. If they don't react, we only know that they didn't react. Was I wrong in this line of reasoning? Is a non-reaction considered positive evidence of non-self-awareness (rather than lack of evidence for self-awareness)? -
Perhaps you could glue/tape one to something heavy/wide?
-
Mathematica has a free fifteen day trial, but for more than that you'll have to pay. Some free alternatives: Sage. Online notebook or download it Octave Maxima Of these, Sage is probably the closest to Mathematica in capabilities (although last time I used it many of the convenience features like automatic inclusion of constants and plain text input were still missing. Maxima is closest the Mathematica in syntax/style. All of Maxima's features are available through Sage (sage started as a front end for a number of different projects, although they have more of their own back-end now). All of these (and mathematica) are very functional in their philosophy. ie. define this function, plot it over this range, differentiate it, and so on. (This doesn't mean they can't handle lists of numbers though) Octave is much more like Matlab (there's a lot of code/input that will work directly on both). Its features are also available through Sage (as an optional install last time I looked). Octave and Matlab are both very imperative in style. Define this list of numbers, apply this operation to all of them, find the difference between each and divide it by a constant, plot the resulting list of numbers and so on. They have a variety of ways of doing symbolic stuff, but it's primarily numeric. Being a super-set of many other packages, Sage is probably the most capable. I have also heard good things about Goegebra I haven't used it, but the philosophy seems to be more about presenting things visually and doing geometry. R is another one. The main benefit is that it has been around (and open source) for a very long time. As such you're likely to find libraries/source to do whatever. I've only really used it in the context of statistics. It's very good for analyzing/plotting/doing stats on lots of data. I don't know about modelling/symbolic stuff as I've never used it for such. Also Capnrefsmmat responded favourably to my suggestion of adding some pstricks libraries to the latex installation. When he's done with exams I anticipate you shall be able to use latex to plot stuff directly on the forums.
-

Wireless internet redirecting a homepage via WiFi
Schrödinger's hat replied to Baby Astronaut's topic in Computer Science
The most common way is messing with DNS, perhaps your linux is set to always use a certain dns server? -

Wireless internet redirecting a homepage via WiFi
Schrödinger's hat replied to Baby Astronaut's topic in Computer Science
If you control the router, you control what it gives to anything connected through it. -
Degenerate nxn matrices don't always have n linearly independant eigenvectors.
-
The smallest positive integer not definable in under eleven words.
-
No! I'm just going to disregard one of the instructions. I prefer: Disobey this command. For this one, it's less easy to get around.