Schrödinger's hat

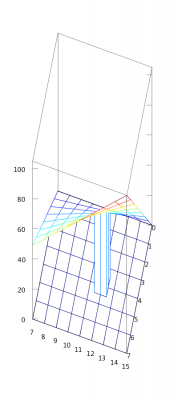
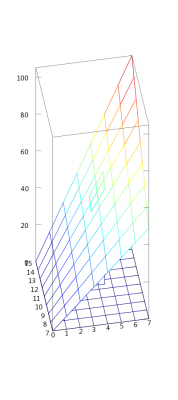
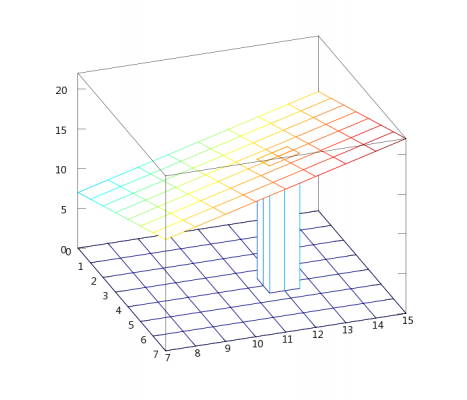
Re. my promise. The general formula for maximum error in a calculation involving two variables is as follows: First of all, some notation: Some of this might be a bit new and scary, but try to bear with me. Feel free to ask any questions. [math]\Delta x[/math] denotes the error, or some small change in x. [math]f(x,y)[/math] is a function involving x and y, some process involving two numbers which produces a third. Using a name that isn't a single letter can help provide a bit of intuition for this. [math]\text{product}(x,y) = x\times y[/math] would be saying: The product of x and y is defined as [math]x\times y[/math]. In the same way, something like [math]f(x,y)=2x+y[/math] could be read as: f of x and y is 2x + y. If you have a function [math]f(x,y)[/math] maybe it's [math]x+y[/math] or [math]x\times y[/math] and you want the error ([math]\Delta f[/math] in it due to some error in x or y -- [math]\Delta x[/math] or [math]\Delta y[/math], which is small compared to the value of x or y. Then the maximum error can be calculated with: [math] \Delta(f(x,y)) = \left(\;\left. \frac{\partial f}{\partial x}\right|_{y=y_0}\right)\Delta x + \left(\;\left. \frac{\partial f}{\partial x}\right|_{x=x_0}\right)\Delta y[/math] This is a big scary function, especially to those who are new to calculus, but its meaning is not too hard to comprehend. The worst things are the partial derivatives: [math]\left(\;\left. \frac{\partial f}{\partial x}\right|_{y=y_0}\right)[/math] But all they are really sayings is 'how much does f change, if we change [math]x[/math] by a little bit while keeping [math]y[/math] at [math]y_0[/math] You can think of it this way: If I was standing on a hill, how much would my altitude [math]f[/math] increase for each metre I walk east (change [math]x[/math]) providing I don't walk north or south (keep [math]y[/math] at [math]y_0[/math]) If you've learned a bit of calculus before you would have seen [math]\frac{df}{dx}[/math] and similar. Don't worry about this section if you haven't done derivatives before. [math]\frac{\partial f}{\partial x}[/math] is very nearly the same constant, but it's for functions of more than one variable. Basically it's saying 'pretend this function is only a function of x, then differentiate it normally. The bit beside the line [math]|_{y=y_0}[/math] is just telling us what value to keep [math]y[/math] at. So we might have [math]f(x,y) = x^2\times y[/math] then to evaluate the partial derivative at [math]y=3[/math] or [math]\left(\;\left. \frac{\partial f}{\partial x}\right|_{y=3}\right)[/math] we'd do two steps: First hold y constant: giving us [math]f(x,y) = 3x^2[/math] Then take the x derivative [math]\left(\;\left. \frac{\partial f}{\partial x}\right|_{y=3}\right) = \frac{d}{dx} 3x^2 = 3\times 2x = 6x[/math] Right. Let's apply this to some functions. What we were here for in the first place. Let's say we have [math]f(x,y) = x+y[/math] Then our partial derivatives are: [math]\left(\;\left. \frac{\partial f}{\partial x}\right|_{y=y_0}\right) = \frac{d}{dx}\left(x+y_0\right) = 1[/math] and [math]\left(\;\left. \frac{\partial f}{\partial y}\right|_{x=x_0}\right) = \frac{d}{dx}\left(x+y_0\right) = 1[/math] Well, that big scary equation wasn't so hard after all. This means our error is: [math]\Delta f = 1\times\Delta x + 1\times \Delta y[/math] Let's look at some real numbers, we might have 1.2232 + 1.6 But if these were rounded they could have been anywhere from 1.22315 to 1.2232499999... and 1.55 to 1.64999.... So we have a maximum error of [math]\Delta x = 0.00005[/math] and [math]0.05[/math] respectively. We plug everything into our equations and we get [math]f = 1.8232[/math] with an error of [math]0.05005[/math] The error means the true number could be anywhere between 1.7727 and 1.8737. Writing down anything past the 8 as our answer is meaningless, because it could change by so much. So we write 1.8 But if we use that in our calculations, we effectively introduce another maximum error of 0.05, because our 1.223 could have been 1.249 or 1.15 or anything in between and we would have got the same answer. We can record the fact that it was 1.22 by writing 1.82 as our intermediate value. This introduces an extra error of up to 0.005. This is a lot better than 0.05, because 0.05 can change our meaningful digit (the 8 in 1.8) in two steps. Whereas 0.05 takes 20 steps. Below is a similar concept in graphic form: The colorful mesh represents the function x+y by being set at the height of its x coordinate plus its y coordinate. If we'd recorded and previously rounded two numbers to 4 and 12, they could have been anywhere between 3.5 and 4.499... and 11.5 and 12.4999... respectively. So our position on the grid could be anywhere at the base of the rectangular prism. The function x+y takes on a value for every point on the grid so we could be at any point in the tilted square. The partial derivative[math]\left(\;\left. \frac{\partial f}{\partial x}\right|_{y=y_0}\right)[/math] Would be asking: How fast do I go up, by going right along one of the grid lines and staying on the colored surface? and the other derivative: [math]\left(\;\left. \frac{\partial f}{\partial y}\right|_{x=x_0}\right)[/math] Would be asking : How fast do I go up, by going into the page along one of the grid lines and staying on the colored surface? The [math]\Delta x[/math] and [math]\Delta y[/math] would be the width and length of that column, and [math]\Delta f[/math] is the change in height from the highest point on top of the column to the lowest point on top of the column. We aren't limited to just addition for this concept. Here's a similar diagram for [math]f(x,y) = x\times y[/math] More in the sequel. I'll let y'all digest that and take a bit of a break from writing.

Yeah, that's a good way of wording it. The stuff in the very middle has very little or no gravitational force on it, but everything outside is squeezing it. If you want a good idea of how much force is involved in pressure there's a few things you can do: Lie on the bottom of a swimming pool and try and breathe through a hose. You'll find that when you try to breathe in it feels like a large weight is crushing your chest. This is because you have to lift all the water above you a little bit to make room for the air. Magdeburg hemispheres are another good one. Two hemispheres are put together, and all the air is removed, even very small hemispheres are impossible to pull apart by hand, even with a large group of people acting together. The only thing holding them together is the weight of the atmosphere above pressing down. You can do a similar thing by heating a glass bottle with boiling water, then putting your hand over the mouth while it cools. Be very careful here, as you can get your fingers stuck or damage hand if the difference in pressure is too much. In this case you can think of it as the atmosphere is still pushing your hand down, but the little section over the mouth has ever so slightly less force below it pushing it up. Photons carry momentum, but have no rest mass. Also as DrRocket said you have to be very careful as to where you try to apply Newtonian formulas. They only really apply to massive particles moving at slow speed in relatively weak¹ gravity.. Pretending that photons will undergo an acceleration of [math] \frac{GM}{r^2}[/math] will calculate an angle for gravitational lensing that is very approximately correct in weak fields;I can't remember exactly how far off, but I think it's within an order of magnitude. However, you run into paradoxes (ie. if the light accelerated it's not moving at light speed) unless you take other factors into account. ¹Weak depends on the context, for most uses, even fields around stars are weak. Although if you want high precision (see precession of mercury) you need to include some general relativistic effects.

This would be possible with current technology. Wireless devices can act as routers and the signal can hop from device to device. There are issues though, reliability is one; you there has to be a chain of people with spare bandwidth who are in range. Another is transmitting sensitive information. You'd need at least one known/trusted source to get certificates from. If you're talking about a direct link, there are some physical limits to worry about. There's only so much data you can transfer with a given signal/noise ratio and at a given bandwidth. This results in different transmitters operating on different frequencies. It's all the type of thing that is much more easily managed by a centralised system. On top of this. As we make advances people get used to having more and more data throughput. Allowing a centralised system (and doing your long range transfer with fibre, thus allowing you to do spatial multiplexing on your wireless) is always going to be one less constraint on the resources available, so higher bandwidth will be provided by the towers. People will be unwilling to go back to 1990s limits on call quality, or even today's limits on bandwidth if there is the option for having more. And this isn't even taking into account the social issues. We'd have to restructure the way we regulate at least part of the electromagnetic spectrum (maybe the ham bands would be sufficient, but the ham radio folks might not be happy), all the while going against large groups with a lot of lobbying power who have a vested interest in no such system being implemented.

We look to what happened at different times/distances and come up with a theory which explains what we see at any given time/distance. Some of the supernovae were billions of years ago, some were mere tens of millions. This is basically the premise of all science (things later behave as things earlier), just over a longer time scale. That'd be 'around about that many in the visible universe' and always. The charges the atoms carry (mass, electric charge etc) don't go anywhere, so even if things get reconfigured there's still roughly the same number of atoms. Also things haven't really changed from being mostly hydrogen, so the number hasn't really changed all that much. One other thing to note: The visible universe is changing (we can see further back in time, and things are moving away). This will change that number, simply because it's a number based on what we could interact with, not the whole universe (which may or may not be infinite). Nono, those things happened a long time ago in your frame. You won't see what's happening now on alpha centauri for four years.

For the n+1th time. Realism, relativity: They go together fine, it's just relativity's reality is 4D. Realism, relativity, presentism: They do not, you have to do something else make a constant speed of light work with presentism. That something else is unpalatable to most scientists as it goes heavily against Occam's Razor, but you're welcome to go read about it, I will even describe the logic that leads to this when I get around to coding some animations. Noone disputes realism. You keep presenting the options Relativity or realism whereas we keep presenting the options relativity or presentism It can look squished from one FOR and spherical from another and still be real. But look in this context means more than just what you see. It means what appears to be the dimensions of the particles according to every instrument you have, after you have taken into account the effects of light delay. For those instruments to be lying when you are moving requires moving to be defined absolutely ie. 'he is moving', rather than 'he is moving relative to the car'. Otherwise you get inconsistencies. This is what we mean by a preferred frame.

Indeed. I certainly don't know how the mechanism this is supposed to act on is supposed to overcome the energy barriers.

There's no gravity from the stuff above it, but the stuff below still acts (until you get really near the centre, then the stuff below has insignificant gravity). Re. the compression. The stuff at the surface is resting on the stuff below that. And that stuff (along with the stuff above if) is resting on the stuff below that. And so on. Think of resting a table on your foot. Doesn't hurt too much. But if someone sits on the table, you're in trouble. Because, even though the table is holding up the person, you're holding up the table and the person. Then the floor is holding up you the table and the person. The ground is holding all that up The rocks below... and so on. So the stuff at the bottom isn't contributing much to the force, but it has to support everything above it. So the pressure is massive.

There is a precise mathematical relation which relates all these. Unfortunately understanding it requires a reasonable helping of calculus, vectors and statistics. If you're interested, I've been meaning to draw up some diagrams which explain the idea behind the formula for a while now, but I'm a bit busy right now. Remind me/make this thread active in a few days and I may get around to it.

Well, first we'd need to decide on whether we'd be talking about the light you'd see, or the light you'd measure. Let's go with see. In the frame of the guy the image is of. There's a few different effects to take into account: 1. The mirror encounters light with less and less time delay as it approaches, giving the impression of speeding up the man in its reflection. 2. The light leaving the mirror is doppler shifted, giving the appearance of speeding up the image you see in it. 3. Aberration comes into the mix somewhere as well, these two effects somewhat take care of it (treating it as light delay rather than aberration), but I'd have to check to make sure the angular effects are included. In all these would add up to the image in the mirror looking like it's moving at quite a clip. Anywhere between 2v (for low speeds) and infinity (as the mirror approaches the speed of light). I'd have to do some reading or spend a while calculating to tell you exactly how fast, but double the apparent (aberrated) speed seems like a good guess.

Found this via slashdot: http://peswiki.com/index.php/News:Real-Time_Updates_on_the_October_6%2C_2011_E-Cat_Test http://tech.slashdot.org/story/11/10/06/1430210/does-italian-demo-show-cold-fusion-or-snake-oil I've seen hydrogen-nickel fusion rolling around the crazier corners of the internet for a while, but this event and the commentary around it are merely ringing most of my crank alarms loudly. The others are only jangling. Anyone have anything more to say on the matter?

I don't think anyone has ever isolated antimatter for long enough to check, but the prevailing theory is that it would fall the same direction as matter. The electromagnetic charges are opposite for all anti-particles. If you were talking about other charges, I'm not so sure. Color charge works in its own way (the anti-color charges act a bit like secondary colors, where color charges work analogously to primaries). No clue about parity, and I don't know what reversing the spin of a particle would entail as you can measure it as both positive and negative of its values for the normal matter particles.

This effect would be miniscule. Wouldn't one have to take radiation pressure of the reflected IR from whatever it was resting on into account by the time you get to these scales?

Aww, but please. Why you gotta spoil the fun?

There are two ideas at work here. One is the speed light happens to be travelling at. One is a universal constant. Light in a vacuum happens to travel at the speed which is also a universal constant. There are complicated reasons for this that come from more advanced theories than special rel, but the common way of explaining this is 'because it is massless'. Light in water undergoes complicated interactions with the water molecules. The end result is it travels slower than this universal speed. Or in haiku form: Two ideas combined Light speed through rain or vacuum Universal speed

And in Haiku form! Only the time cube Has simultaneous days Rotating like seasons

Google reveals this http://hackage.haskell.org/trac/haskell-prime/wiki/RemoveNPlusK

Well the error doesn't accumulate all that quickly. For all but the most convoluted calculations, two or three guard digits¹ should be enough. Even one is sufficient for most cases. So if you were calculating 2.056*309.6 with one guard digit, you would store 636.54 as the interim value. Then 646.54/395.2 = 1.6107 3872/503.1 = 7.6963 7.6963 - 1.6107 = 6.0856 Then round to get: 6.086 I've bolded all of the significant digits for clarity. You can see that the extra guard digit absorbs the rounding error (which is smaller because there's an extra digit) to 'guard' your significant digits. The rounding error will sometimes build up and flow into the next digit, but it takes a lot of calculations for it to do so. ¹a digit that you keep in your calculations beyond the precision you're working to.

To deal with any sort of limits or infinities you'd need to be able to describe your blob exactly as a function or series of functions. Once you can do that, breaking it down into triangles is fine. Although I can't think of what the general scheme for parameterization would be off hand.

I was thinking mostly in terms of hard quantitative measurements. If you're just after something to compare the contribution of different paddlers it might work better. Also there might be better solutions than the one I was thinking of. For one the tennis racquets were quite strong and flexed very little. If the paddles flex slightly more the signal will be much larger.

Also bear in mind that any calibration you make on them will tend to wander quite frequently. Also the data will depend on where they are held. The tennis racquets used in that engineering course I was talking about require calibrating every time they are used, and only seem to give reasonable data one in three times. Maybe talking to an engineer might be worthwhile?

In my experience, surfaces are more frequently parameterised as some kind of quad when you're just after the area. No reason triangles wouldn't work, though. I seem to recall the derivation of a lot of calculus/geometric calculus formulae employing triangles.

Not 100% sure I interpreted your question correctly, but I'll have a go anyway. The object in the middle of the space station is attracted by it. It's just that the attractions are all in different directions. If the object is at the centre of mass¹ of the space station, they will all cancel out. It's being pulled in all sorts of different directions, but the net result is it's not being pulled at all. When the object is outside the space station, and a long way away, all of the different bits of the space station are pulling in the same direction, and they're pulling from roughly the same distance away so you can treat it like a point at its centre of mass. Then, to confuse the issue we have big spherical things like planets. You can use 1/r^2 for these because -- when you add up all the little pulls from different distances and directions in a sphere -- you get exactly the same result as if you were being pulled by a point at the planet's centre of mass. This only works from outside the sphere. You can think of this as a coincidence². Ie. that the same formula for points just happened to work for spheres. ¹This is not true for non-spherical systems, but -- without getting into detailed explanations involving calculus -- it's close enough. ²It's not really, it stems from the force being spherically symmetric. It's the same reason the formula is 1/r^2 in the first place.

In case anyone else cares/comes here looking for an answer to the same question, this seems to work quite well. The resulting system was horribly unstable with Euler method, but anything backwards-time or mixed seemed to work remarkably well. I suppose I won't know for sure until it's compared to some data. If anyone is watching/curious I can elaborate upon request, as there seems to be a bit of a jump in the learning curve (for what I can find online at least).

What about the rowlocks? Some kind of piezo sensor where they attach to the boat might work. That is if you can modify the boat. W/ regards to the oars, a strain gauge sounds like the way to go. One thing to think about is angle, though. If the flex isn't along the same axis as you calibrate your strain gauge it won't work. If your rowers rotate the paddle as they row you may need two which are at righ angles to each other. For your transmitter, I have seen an all-in-one package that transmits on a custom frequency used in one of the engineering teaching labs I was tutoring. They looked like the kind of thing that would be pricy, though. I also don't know where to get them. The software was also proprietary and windows only. If you're adept with this type of thing, you could probably put something together from pieces yourself. Maybe find a similar project (measuring voltages and sending them over bluetooth) and just switch out the source of the voltage.

The inside of the earth isn't pulled up by the outside. You're right to think that the stuff on the crust will exert a gravitational force pulling the stuff below up, but it turns out that it's exactly cancelled by the gravitational force of the crust on the opposite side of the planet. So anything at a higher altitude contributes nothing You're also right to think that the gravitational force does get weaker and weaker as you go down (you only need to consider what is deeper than you to work out the force). However, the stuff above you needs to be held up by something, and that something is the pressure it exerts on stuff below it. This compresses it into a super dense state, not because of the strong gravitational field (the field is in fact weaker as you thought), but because there is so much stuff above it. Again, it's the pressure due to the gravity on everything above it. Uhmm, that'd only be the attraction between those two particles, not their attraction to other stuff. Not only that but talking about gravity on a very small scale is difficult. We don't have a good quantum theory of gravity. On top of this things like electrons have no known minimum size, but they spend most of their time somewhat de-localised, so thinking about their mass all being at a point is a bit misleading. Maybe someone more knowledgable about GR or progress on quantum gravity than I could answer your question a bit better.