TaoRich

Hundreds. Much obliged. All sorted. [ and apologies to the mods for posting in the wrong forum ... didn't see this one before ... am aware of it now ]

Hello, I see at the bottom left hand side of some (most) people's profile page: Latest Visitors I don't see that on my page. Is that a setting / option / view preference ... ... or am I being a bit thick somehow ? Advice appreciated ! Rich

I'm not sure what you mean by "do the coordinates advance in spherical lines ?" Can you elaborate ? That relates to what I am on about - it's the direction that is significant. With regard to other comments above about rotation through 180 degrees, or taking the absolute, I'll re-express my query yet again in other terms: [1] We can fold or reflect a one dimensional system about a point of symmetry: By way of example, take the number line argument: we can take a value of n and reflect that value about the zero point to give us -n. [2] We can fold or reflect a two dimensional system about a point of symmetry or an axis of symmetry: By way of example, we can take co-ordinates (x,y): a) and reflect the x value about the x axis zero point to give us (-x,y) b) or reflect the y value about the y axis zero point to give us (x,-y) or c) reflect the x AND y values about any line or axis we chose within (x,y) Cartesian system a) and b) are reflections about one dimension c) is a reflection about two dimensions [3] We can fold or reflect a three dimensional system about about a point of symmetry or an axis of symmetry: By way of example, we can take any co-ordinate system for our three dimensions, say (x,y,z) or (r,θ,φ): a) and reflect the x value about the x axis zero point to give us (-x,y,z) b) or reflect the y value about the y axis zero point to give us (x,-y,z) c) or reflect the z value about the z axis zero point to give us (x,y,-z) or d) reflect the x AND y values about any plane we chose within the (x,y,z) Cartesian Coordinate system or the Spherical Coordinate system(r,θ,φ) a) b) and c) are reflections about one dimension d) is a reflection about two dimensions To visualise what I mean by d) consider holding up a mirror in a room: You can angle the mirror to reflect the 3 dimensional world about any plane you chose.You can reflect your left hand to become your right hand (and vice versa)Back now to my exploration / query: What happens when we reflect 3 dimensions about 3 dimensions ? Not changing the sign of a one or two dimensional vector or radius. Not rotating the 3 dimensional object through some angle If we view a sphere in our 3 dimension reality ... and then we reflect that sphere about all 3 dimensions ... what would the reflection sphere look like ?... where would it be ? - - - Please note that I am not trying to solve any particular problem, or come to grips with any existing mathematics. I'm exploring ... questing, questioning. ( Yes, I'm talking about the edge or fringe of our physical reality, not a "conventional view of our reality" ... but bear in mind in Mathematics, we can manipulate numbers, descriptions, objects, fields, planes into "non-physical realms" and "unreal dimensions". )

Let me try to express my question in a different way: Consider a sphere alpha which expands in radial symmetry about an origin from radius r = 0 to radius r = R So, at any given point in time, the edge of the sphere alpha can be determined by taking a vector radius r(t) and "swinging it around in all directions". Then consider a sphere beta which expands in radial symmetry about the same origin from radius r = 0 to radius r = -R Again, at any given point in time, the edge of the sphere beta can be determined by taking the vector radius r(t) and "swinging it around in all directions", except now the radius r(t) will be 0 or negative. In relation to our original sphere alpha, where does sphere beta exist ? Our sphere alpha covers all positive value for r. Where do negative values for r lie. Or expressed another way: Positive values of r are "outwards from our point of origin". How do we describe the "space" or "sphere" where r goes "inwards from our point of origin". In my mind, sphere beta is the inverse of sphere alpha (and not some rotated view of alpha). It is sphere alpha extruded in the opposite direction. Is there no mathematical term (along the lines of orthogonal or something like that) which expresses the relationship between sphere/space alpha and sphere/space beta ?

In your example, in Spherical Co-ordinates the centre is the zero-point of the number line. Positive values of R will cover all points on the sphere. Where are the negative values of R located ? Rotating through 180 degrees makes no sense in the context of a 360 plane. Considering that there are two 360 degree planes in the spherical co-ordinate system, it makes even less sense. ???

Hello Folks, [1] Can someone please explain that bold text in a bit more detail ? When is it convenient (under what contexts) ? [2] If we define a sphere in spherical coordinates, with the centre at the origin, and a positive radius R If we then change the sign of the radius to -R what are the implications Where does this "new sphere" exist in relation to the old sphere ? (a) in mathematical terms (b) in practical reality Cheers Rich

Back in my University days - during Maths I and Physics I - for some reason I was deeply uncomfortable with the "foundation on which the higher-level arguments" were built. I always felt there was something missing - that there was something "shaky" at the root. Somehow I had this (intuitive) feeling that I was being led into a house of cards, but I could never quite work out from whence exactly my discomfort stemmed. That's what started me off on this 15 year track of investigation. "What if these primitives that we take for granted shouldn't be taken for granted. Do they bear further investigation ?" In my exploration of this "topic" I often feel like a janitor in a Physics Lab lifting up the carpet to see what is underneath. I'm not saying that any of Physics has it wrong - it's just that I resent anything I can't understand. I'm not content to walk on the carpet and take it for granted - I need to understand for myself what supports it.

Morning folks, Brain a bit clearer now, and the first thing I noticed was my botching of the topic question: What do we men by space ? Should actually have been: What do we mean by space ? Now on to the responses - thanks again to all who have commented. I must make it clear, I am asking about science here and not philosophy. I'm stepping backwards in first principles, right down to the "zero'th" principle. My starting point(s) for my question here (and for the paper I am working on) is this/are these: nothing exists no-thing exists no space exists time has not yet begun I'm working on defining the physical nature, behaviour, characteristics and properties of the very first elemental fundamental space to emerge from the nothingness. It emerges out of no-where. Prior to its emergence, there is no other space It does not expand into an existing space It does not expand within any existing framework As it expands, it creates the very first space. As it expands, it does so over time, and hence space-time emerges from the emergence of this fundamental space. - - - Revisiting my initial "definition" I think this might be slightly better: We define "space" to be a fundamental field with properties of: dimension volume Again, to repeat myself, I'm not musing philosophically. I'm setting out to: define a formal mathematical and physical model of an fundamental self-emergent quantum space "cell" where the "space cell" is comprised of interacting "elemental spaces" from which I derive a (dynamic) field density equation across the profile of the interacting spaces which I believe will provide insight into a basis for quantum gravity

If we want to talk about the "origin of space" or the "emergence of space" as a first principle - before we introduce anything inside it ... what is it that we are actually referring to ? Sometimes the simplest questions are the hardest: "What do we mean by 'space' ?" Outer space ... sure that's easier to define: But what is "space" as we commonly refer to it, the "framework": in which we exist in which "things" exist in which we define and conduct experiments, observe the results and interrelationships, and deduce conclusions How do we define this "framework" from first principles: "Something" with: dimension volume or capacity (to store or house something) Is that complete ? Are both conditions necessary ? Are they sufficient ? And what is the "something" ? { Too tired to engage my brain to find a better word for now. }

You have to be a bit patient with a fountain pen, use one with a gold nib, and choose the right nib to suit your style: thin, medium, fat Then, as you write, the nib wears itself to fit the precise angle that your hand-grip creates in alignment with the paper. Once you've worn it in, you'll find it glides like silk. That's also the reason why you shouldn't casually borrow someone else's fountain pen - your hand angle stuffs up their groove.

a more general theoretical consideration of a given problem Yep. That's what I am doing ... it's a "theoretical thought experiment" and not a "we performed the following actions". I'm asking my reader to consider a possible scenario, rather than expounding on what we/I have physically investigated. Well spotted. Can I draft you as a sub-editor/proof reader when I've finished my paper ?

Thanks. Again however with the term inverse, we've got: additive inverses which adds to zero multiplicative inverses which multiply to one Here's a quotation which may help focus my query and the discussion: So when we "cleave zero into symmetrical complementary pairs" what do we call those pairs ?

Greetz, What is the correct term for "pairs of opposites" that "cancel to zero". For example: 7 and -7 cancel to zero if added identical rising and falling waves cancel to zero if they interfere at a point where their amplitude is precisely the same a particle and an antiparticle cancel each other out if they interact The word complementary seems to describe the relationship quite well, but there are (many) very specific uses in Maths & Physics. So we'd hit some confusion there. The word symmetry also seems to describe the relationship quite well since we could say: 7 and -7 lie symmetrically opposite from each other in equal distance from (the reflection plane) 0 identical rising and falling waves lie symmetrically opposite from each other in equal distance from (the reflection plane) 0 amplitude a particle and an antiparticle are symmetrical and opposite But again, symmetry has formal specific meaning in various Maths & Physics contexts. I've been hunting around for a term in common usage - but not much luck thus far. Can anybody help with a reference or some suggestions ? I'd like to use it in the context: 7 is the ________ of -7 a rising wave is the ________ of a falling waves with identical amplitude a particle is the ________ of an antiparticle I'm inclined to lean towards: A particle is the symmetric complement of an antiparticle But I'm acutely aware that inventing a new language, or using established formal terms in a sloppy fashion is not a good way to earn respect or be taken seriously. Cheers Rich

I'd convey that same information as: "The passive voice is more pleasant to read and write. Content and clarity is more important than notes on style - consistency is key to clear writing." I seldom preface anything I say with "In my opinion ...". If I'm feeling confident enough to express my opinion, I express it factually, and with conviction.

I've managed to solve my problem. I was thinking too loosely and grasping for an analogous illustrative example, when I should have rather tried to think more tightly and discuss what I have at hand, instead of making flawed parallels. For completion sake however, I wanted to get a proper understanding of my own bouncing ball question, and a decent answer. So here goes: http://en.wikipedia....wiki/Hookes_law The force exerted by the spring in SHM increases with the magnitude of the stretch or displacement. Even though gravity is a constant force pulling down on the sprung weight, the spring force upwards varies. So that is not the same as the (constant) force of gravity pulling on a bouncing ball. Looking now at a pendulum: http://en.wikipedia.org/wiki/Pendulum Again, we don't have true SHM. Thanks for the comments. All helpful as usual.

Lovely .. thanks ... helpful I'll bend the word and concept of "absolute" to fit into my explanation. Above 'the line', I have "a space designated as alpha" which "interacts with a second space designated as beta". It's this initial interaction that I need to explain first (to my audience). I need to get the understanding of the "same world" interrelationship clear. Hence my desire to simplify things at the outset for the first pass across the model. Once this is clear, I'll move on to the next step: Below 'the line', I have complementary relationships "(anti)space anti-alpha" "interacts with (anti)space anti-beta". That's too much to get across/grasp in one pass. It hurt my head for a few years trying to come to grips with that myself !

Thanks for the input. I realised after I went to bed last night that I didn't make it clear that i was referring to a ball bouncing vertically up and down on exactly the same impact spot, and not a ball bouncing with transverse motion as well as vertical. Mentioning it now for clarity sake, but I think that most of you got that first time around. Do you mean that the movement path will follow a parabola or that the rate of fall/climb will be parabolic ? If the gravity is a constant force, apart from the turnaround bounce point, surely the behaviour is the same as a SHM spring oscillator ? Yep. We'd have the ball squishing and deforming, absorbing kinetic energy, and then "expelling" that energy again. In golf ball design alone, that alone is probably a multi-million dollar annual research exercise. Oh, I Gimp-hacked a Wikipedia Sine Wave just to illustrate a point. Which is (to my mind) the same as reflecting the sine wave ... open to opinion/correction. Luckily, I don't actually need this for my "thoery paper". At this stage, I was looking for a "illustrative example" to simplify my initial description of my expanding/collapsing fundamental space cycle. My modelling is truly sinusoidal SHM, but the part which drops below the line requires me to bring in the concept of an anti-space too early in my discussion. I need to make an initial gross simplification of the expansion/contraction cycle to discuss the "mechanics of the conservation of space", before i drag the reader into a fuller and more complete description of the true cycle (which will require some leap of the imagination). I'm not sure how much of this makes sense (it's probably off the wall for most people) but the comments and opinions are really helping me. So again - much appreciated. Rich

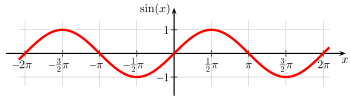
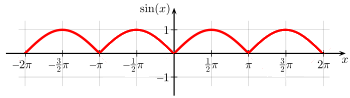
Hi, Something I pretty sure about was thrown into doubt this evening by some opinions outside this forum. I'm hoping someone can put me back on track and into my old comfort zone. What is the behaviour describing a perfect bouncing ball in a lossless system ... Now I know it's not true Simple Harmonic Motion (SHM) since we have at one end: the bouncea high-speed drop reaching maximum velocity an 'instantaneous' reversal of direction a high-speed climb starting at maximum velocity [*]the apex a slowing of the rate of climb from maximum velocity to 0 an 'instantaneous' reversal of direction an accelerating rate of fall from 0 to maximum velocity So we definitely do not have a complete sinusoidal wave This is not what we have: But am I correct in assuming this is what we have: Half a sine wave, repeated. Essentially, to my mind, isn't the wave motion reflecting about the X axis, just as the ball is reflecting about the point of its bounce impact. Whereas in true SHM, the wave motion passes through the X axis, just as a pendulum would pass through the trough point of its swing. Comments ?

I'll try latex as per the post above. It sounds promising. Thanks for the kind offer - appreciated. I'll press ahead trying out the first steps on my own ... but I'll yell for a bit of help if I get tired of hitting my head against a brick wall. What I need is pretty simple, maybe 6 or 8 diagrams total. Even If I have to use Gimp, it's not a train smash. Once I've worked out what visual elements I need to get the first line drawing looking reasonably 3D, I can resize and rework the 2D circle and elliptical perspective components to get the various stages in my progression. I just really need to illustrate a start-space and an end-space, and a few shell slices to explain a few step-wise progressions over time. The two spheres/spaces that need to be superimposed are symmetrical/identical in all ways so I can re-use and simply re-shade in a complementary colour. The diagrams need only to be a "visual aid" to imagination and explanation, rather than a "dissection and labelling of the mathematical beast". I missed this post in the middle of my response flurry. Ohhh ... lovely ... I might bug you for some help via PM Definitely going to try Sketchup on the other commercial side of my boot sector. Downloading Archimedes now. - - - I do some testing of them all tomorrow. I'll put up some opinion and sample pics as I make progress ... or scream for help if I don't seem to be making headway. Again, I'm loving being here ... you people are so friendly and helpful ... pleasantly surprised and very grateful. Cheers Rich

LaTeXDraw is a free PSTricks code generator or PSTricks editor for LaTeX. It has the usual drawing tools (lines, rectangles, circles, Bezier curves) and can resize, rotate, move and join objects using vector transformations. LaTeXDraw uses SVG as its file format and figures can be exported as PSTricks code, pdf, eps, jpg, bmp, png, ppm.PSTricks is an extension of LaTeX which allows the creation of drawings, diagrams and graphs in 2D or 3D. Sounds promising ! Right there in my Ubuntu Software Centre. I'll let you know what I think of it when I've pulled the 178 MB down overnight. Thanks for the suggestion.

In the words of the immortal bard: "Aye, there's the rub." I'm downloading Google Sketchup and will check it out - as soon as I reboot into Windows. If it looks useful, I'll try to get it running under Wine on Ubuntu. Thanks for the suggestion.

ajb You broke Dictionary.Reference.com http://wordsmith.org/words/nosism.html nosism (NO-siz-em) noun The use of 'we' in referring to oneself. [From Latin nos (we).] As it's often used by editors, it's also known as the "editorial we". It's also called "the royal we" owing to its frequent use by royalty. Mark Twain once said, "Only kings, presidents, editors, and people with tapeworms have the right to use the editorial 'we'."

Greetz, I need to draw spheres, with a decent 3D representation - the figures will be used to explain my argument. I'm going to need to illustrate the sphere: expanding, and contracting show radius of the sphere at various stages of the expansion/contraction show slices/shell sections at various time intervals Then I'm going to need to superimpose one sphere inside the other and illustrate: interrelationships between the spheres I saw this diagram in one of the posts here in the forum: That's pretty much along the lines of how I'd like my figures to look. A simple line diagram, with a clear 3 dimensional visual element. Can anyone suggest any simple drawing program I can use ? Preferably something that will run on Ubuntu Linux. Preferably something simple and easy to use. I've got blender and a bunch of other 3D modelling packages installed already, but have not yet put a huge amount of effort into surmounting the learning curve. They seem a bit like taking a sledgehammer to kill an ant - wayyyy to heavy for the simple job I have at hand. I'm hoping there's something better suited to quick easy mathematical/geometric diagrams. Cheers Rich