Duda Jarek

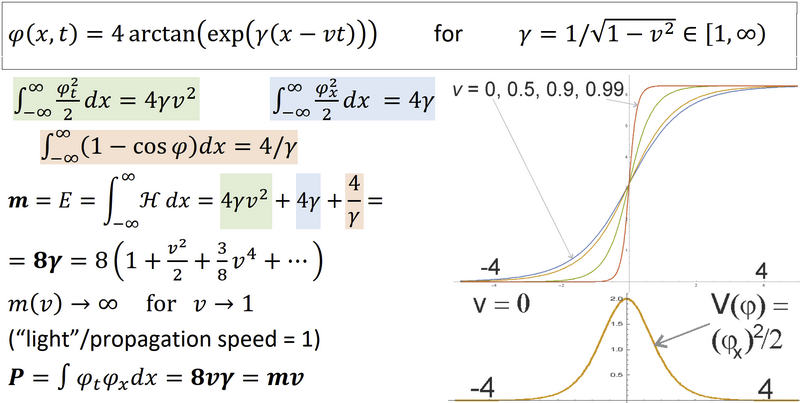
Energy density, Hamiltonian is a first step - convenient to start with as all the terms have positive conteibutions. It is often timespace symmetric - not distinguish time and space directions. But for solving such model we indeed usually go through the Legendre transform to Lagrangian - both for the least action formulation, and the Euler-Lagrange equation. I have tried to go this way for the biaxial nematic with Coulomb interaction, but it was too tough for me. Hamiltonian alone can be used to find static solutions, like this kink in sine-Gordon as minimal energy transition between two vacua. However, electron should be finally a dynamical solution - with this zitterbewegung, de Broglie clock ~10^21 Hz oscillations, confirmed experimentally: https://link.springer.com/article/10.1007/s10701-008-9225-1q

Let me bring back my two responses, both are crucial for the model: The number of found particles is in hundreds/thousands now. Some are virtual, like 80GeV boson W in beta decay of 1GeV neutron - this mass should be rather imagined as only shape of energy dependence like for https://en.wikipedia.org/wiki/Effective_mass_(solid-state_physics) What we should target (as configurations being local energy minima) are especially more stable particles and their decay modes e.g. from https://en.wikipedia.org/wiki/List_of_baryons ... and a general behavior in this table is decay with pion or kaon to baryon with lower strangeness. As discussed, there are many reasons to imagine baryons in this biaxial nematic perspective as loop of one vortex around another vortex. We have three types of vortices, allowing for quark-like interpretations. Possible complication of such simplest knot is additional internal twist of its vortex loop around - it should be obtainable in high energy collisions, and should relax by releasing part of this twist as particle - pion, kaon (bottom of diagram below) ... getting nice agreement if interpreting the number of internal twists as strangeness. There are considered strageness 4 baryons (e.g. https://arxiv.org/abs/2011.05510 ). The space of local minima of configuration space can be quite complex: 3 types of vortices, they can contain charge (e.g. hedgehog), additional twist for loop around - can lead to hundreds of metastable states for baryons. In these models we have energy density (Hamiltonian, can be translated to Lagrangian) - usually with some spatial derivatives like stress, temporal for kinetic behavior, and potential (e.g. Higgs-like) ... integrating energy density we get mass of particle, usually scaling as in SR thanks to Lorentz invariance. Unfortunately it is quite tough calculation, I have attached for kink of sine-Gordon a few posts ago. We can parametrize with positions of ansatz configurations like hedgehog, Lorentz transformed for velocities, getting classical mechanics approximations ... with kinetic energy going into mass exactly as in special relativity. Fluxons are quite complex. While they are usually studied in superconductors/superfluids, here they are also needed in vacuum, e.g. to bind nucleus against Coulomb repulsion. Probably the best experimental argument are "magnetic flux tubes" - nearly 1D shining structures seen in Sun's corona, they carry energy density per length - which can be released while shortening in https://en.wikipedia.org/wiki/Magnetic_reconnection Quote from "Physics of Magnetic Flux Tubes" by Ryutova: "Vortices in superfluid Helium and superconductors, magnetic flux tubes in solar atmosphere and space, filamentation process in biology and chemistry have probably a common ground, which is to be yet established. One conclusion can be made for sure: formation of filamentary structures in nature is energetically favorable and fundamental process. "

studiot, I had long fluxon response, response about baryons and strangeness - both disappeared. This sine-Gordon kink represents solution minimizing energy e.g. in lattice of pendulums: of phases while twisting by pi. But this is the most basic model - you can find it in hundreds of books and papers - please start with looking closer at external sources.

Please formulate a question and I will try to answer. Sure the basic one is why I haven't moved it forward with simulations ... because the details are tougher than it sounds. To make Gauss law count winding number/topological charge as in Faber's approach, we need to define EM field as curvature of such SO(3) biaxial nematic field, then use EM energy density: as sum of squares of these curvatures. Below is such approach, using representation as 3x3 real symmetric tensor, with Higgs-like potential: preferring some set of 3 eigenvalues - shape of nematic in SO(3) vacuum. One difficulty is translating such energy density from rotation matrix O to the actual tensor M (quite subtle). Second is getting Euler-Lagrange equation (I wasn't able to get), or work on ansatz avoiding them. Third is choosing details of this Higgs-like potential, in fact containing weak and strong interactions. It was too tough for me and I gave up, hoping to find help.

Maxwell equations have this weakness of allowing for any real electric charge, while nature has charge quantization at heart - only integer charges are allowed (at least asymptotically: far from particles). We can repair this disagreement e.g. by making Gauss law count winding number/topological charge (Faber) - which has to be integer ... then its simplest nontrivial charge becomes a model of electron - the question is how to expand it to get all the particles?

The number of found particles is in hundreds/thousands now. Some are virtual, like 80GeV boson W in beta decay of 1GeV neutron - this mass should be rather imagined as only shape of energy dependence like for https://en.wikipedia.org/wiki/Effective_mass_(solid-state_physics) What we should target (as configurations being local energy minima) are especially more stable particles and their decay modes e.g. from https://en.wikipedia.org/wiki/List_of_baryons ... and a general behavior in this table is decay with pion or kaon to baryon with lower strangeness. As discussed, there are many reasons to imagine baryons in this biaxial nematic perspective as loop of one vortex around another vortex. We have three types of vortices, allowing for quark-like interpretations. Possible complication of such simplest knot is additional internal twist of its vortex loop around - it should be obtainable in high energy collisions, and should relax by releasing part of this twist as particle - pion, kaon (bottom of diagram below) ... getting nice agreement if interpreting the number of internal twists as strangeness. There are considered strageness 4 baryons (e.g. https://arxiv.org/abs/2011.05510 ). The space of local minima of configuration space can be quite complex: 3 types of vortices, they can contain charge (e.g. hedgehog), additional twist for loop around - can lead to hundreds of metastable states for baryons.

In these models we have energy density (Hamiltonian, can be translated to Lagrangian) - usually with some spatial derivatives like stress, temporal for kinetic behavior, and potential (e.g. Higgs-like) ... integrating energy density we get mass of particle, usually scaling as in SR thanks to Lorentz invariance. Unfortunately it is quite tough calculation, I have attached for kink of sine-Gordon a few posts ago. We can parametrize with positions of ansatz configurations like hedgehog, Lorentz transformed for velocities, getting classical mechanics approximations ... with kinetic energy going into mass exactly as in special relativity. Fluxons are quite complex. While they are usually studied in superconductors/superfluids, here they are also needed in vacuum, e.g. to bind nucleus against Coulomb repulsion. Probably the best experimental argument are "magnetic flux tubes" - nearly 1D shining structures seen in Sun's corona, they carry energy density per length - which can be released while shortening in https://en.wikipedia.org/wiki/Magnetic_reconnection Quote from "Physics of Magnetic Flux Tubes" by Ryutova: "Vortices in superfluid Helium and superconductors, magnetic flux tubes in solar atmosphere and space, filamentation process in biology and chemistry have probably a common ground, which is to be yet established. One conclusion can be made for sure: formation of filamentary structures in nature is energetically favorable and fundamental process. "

I again recommend sine-Gordon model to understand massive particles - containing rest energy which can be released in annihilation, also working as inertial mass due to Lorentz invariance ... and such particles can only approach the propagation speed c, at cost of energy growing to infinity, it cannot exceed this velocity. It is safer to directly target experimental properties like charge distribution - which is also suggested in this"biaxial nematic field" ... then interpret fractional charges as quarks, interaction between them as gluons and pions. Another big hint is deuteron - we know it has large electric qadrupole moment ( https://en.wikipedia.org/wiki/Deuterium#Magnetic_and_electric_multipoles ) - hard to imagine for just proton+neutron, but suggested in the discussed model: neutron needs charge, so proton shares part of its charge - leading to savings as binding energy, and observed quadrupole moment. Topological charge is the winding number for function f:S->S from e.g. sphere around some point, into e.g. sphere of vectors Winding number of this f:S->S functions can be obtained by integrating over Jacobian, which is curvature of this vector field - getting Gauss law as Gauss-Bonnet theorem, with built in charge quantization as topological:

If you look at the big framework diagram above, for many reasons baryons resemble simplest knots: one vortex around another, proton/neutron should be such lowest energy pairs ... then they can form various size knots: nuclei (binded against Coulomb), including halo neutrons ( https://en.wikipedia.org/wiki/Halo_nucleus ) stably binded in distance a few times larger than standard nuclear force. The external vortex loop enforces partial hedgehog-like configuration in the center vortex - proton can just enclose it to entire hedgehog, what means +1 topological charge - corresponding to elementary e electric. But neutron has to compensate this partial hedgehog/charge to zero, what requires increased size and so larger energy/mass ... while asymptotically we have charge quantization (as topological), locally there can be such partial configuration/charge like quarks, but it comes with additional energy. Here are a few sources also claiming such charge distribution for neutron: positive core, negative shell: https://inspirehep.net/literature/1377841 , http://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=30&page=119 , http://www.phys.utk.edu/neutron-summer-school/lectures/greene.pdf :

@joigus, these are matters of interpretation, e.g. in perturbative QED interpretation Coulomb interaction is performed with photon exchange ... Should we really imagine some infinite sequence of exchanged photons e.g. between proton and electron in hydrogen atom? Or maybe should we remind that it is perturbtaive approximation - like expanding into Taylor series and representing terms of this series - where Feynman diagrams mathematically came from. In liquid crystal we get Coulomb-like long range interaction because the further e.g. opposite topological charges are, the larger total energy (stress) of the entire field is, e.g. with V(r) ~ 1/r behavior for Coulomb: In perturbative approximation you could get Taylor series and imagine it as photon exchanges, but this is just a different interpretation. So it is safer not to focus on interpretations first, but directly on particle behaviors like Coulomb interaction, decay modes - on agreement there first, then search for correspondence with perturbative QFT approximation of the Standard Model. What particle behavior you think is wrong in the framework I have presented? It also e.g. gets fractional charges in neutron ("quarks") - explaining why it is heavier than proton. Its topologically nontrivial vacuum requires Higgs-like potential corresponding to mass of particles - it allows to deform electromagnetism into other interactions in the center of particles - to avoid the infinite energy of electric charge issue.

I don't understand what do you mean by abstract space? E.g. sine-Gordon has mechanical realization as in the video, interaction between topological solitons is realized e.g. between fluxons in superconductors, long-range interaction is realized in liquid crystals (e.g. https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract ). This is about finding field and Lagrangian to get similarity with particles and fields - also the very real EM field. About repairing this very real EM field: that Gauss law in nature only returns integer charges ... what is done here by interpreting charge as topological, with Gauss-Bonnet theorem as Gauss law ... then the simplest nontrivial charge becomes a simple model of electron. This "biaxial nematic field" can be realized with a real symmetric tensor, exactly as stress-energy tensor in general relativity, by just using Higgs-like potential for it: preferring topologically nontrivial vacuum e.g. S^2, SO(3). But it is safer to be agnostic about its realization for this moment - first get the particles rights, then try to interpret the field e.g. with GR stress-energy tensor or some superfluid vacuum.

Sine-Gordon: just phi_tt = phi_xx - sin(phi) has already massive particles with quantized topological number, pair creation/annihilation, and entire special relativity: Lorentz contraction, time dilation, SR mass/momentum scaling ... studying this looking trivial toymodel is the best way I know to really feel the special relativity. Going to higher dimensions, here is example of observing long-range F~1/D force for topological solitons in liquid crystal: https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract We can choose dedicated Lagrangian to get exactly Coulomb interaction for them with included charge quantization as topological - e.g. Faber's way ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) : define EM field as curvature of some deeper vector field, this way Gauss law counts winding number - topological charge. But the goal is getting all the particles/interactions with dedicated field and Lagrangian - I have a framework, a sketch of Lagrangian, but getting the details + simulations was too difficult for me. Here is the sketch of this general framework again I would gladly discuss - for superfluid biaxial nematic field - of 3 distinguished axes: 1) we get 3 hedgehog realizations of one of 3 axes - kind of 3 leptons (the same charge, different energy/mass), with magnetic dipole due to the hairy ball theorem, Faber's approach gives Coulomb interaction for them, 2) the simplest vortex loop resembles neutrino: stable - very difficult to interact with, 3 types: along one of 3 axes, can "oscillate" between them by internal rotation, are produced in beta decay, 3) loop with internal twist (hopfions?) might correspond to mesons, number of twists nicely fits strangeness - agrees with decay of mesons, strange baryons ( https://en.wikipedia.org/wiki/List_of_baryons ), 4) if another vortex goes through such loop, it nicely resembles baryons, interaction between its vortices creates charge inside (diagram below). Proton just closes this charge, while neutron has to compensate it - what is costly, explaining why neutron is heavier than proton (also quark-like fractional charge distribution), 5) combining baryons form nuclei as various size knots - binding them against Coulomb repulsion, including halo neutrons binded in much larger distance ( https://en.wikipedia.org/wiki/Halo_nucleus )

This thread was supposed to be general as in title - about "Similarity between particle physics and macroscopic quantum phenomena like fluxons?" ... and sine-Gordon is just one of well established basic toymodels here.

But I have also sent you video of somebody's demonstration (e.g. https://www.youtube.com/watch?v=nl5Qq5kUbEE ) ... sine-Gordon is an old well established model: with varying number also of massive particles, behaving exactly as in special relativity ... in looking trivial model - just: phi_tt = phi_xx - sin(phi).

See e.g. the mechanical realizations of sine-Gordon - lattice of pendulums connected by a spring. Rotating them from one side, you get v=0 kink - going from one minimum of potential to the next one: rotated by 2pi. Here on slide 11 you have derived formulas, mass/momentum scaling as in SR: https://www.dropbox.com/s/aj6tu93n04rcgra/soliton.pdf

The "constant velocity" can be just v=0 ... especially that these are usually Lorentz-invariant models: allowing to change frame of reference to make the constant velocity zero. In this case, massive solitons scale mass/momentum exactly as in special relativity - they go to infinity while approaching propagation speed. See the sine-Gordon mentioned a few times, realized mechanically, or similar phi^4 - here is resting kink from https://en.wikipedia.org/wiki/Topological_defect#Images Here are initially two opposite topological charges traveling with constant velocities, which meet and annihilate - releasing mass (energy) as massless radiation (usually traveling at maximal - propagation speed):

The basic definition of soliton from https://en.wikipedia.org/wiki/Soliton is "In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity." For example with electron there comes E ~ 1/r^2 electric field, "while it propagates at a constant velocity" - doesn't it make electron formally a solitons? What more e.g. electron is than "sum of its fields"? Let me quote Einstein again from 1961 Infeld "Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta.": Regarding quantum effects for solitons, many are observed e.g. in superconductors/superfluids - I have started this thread with: There are also observed hydrodynamical analogues of many quantum phenomena, like Casimir, Aharonov-Bohm, orbit quantization etc. - gathered lots of papers: https://www.dropbox.com/s/kxvvhj0cnl1iqxr/Couder.pdf

ps. Very related: "Annihilation dynamics of topological defects induced by microparticles in nematic liquid crystals" - also long-range interactions (F ~1/D formula (1.2) below): https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract

Maybe let me briefly elaborate how I would hope to get all the particles from the biaxial nematic-like field (?), would gladly discuss: 1) we get 3 hedgehog realizations of one of 3 axes - kind of 3 leptons (the same charge, different energy/mass), with magnetic dipole due to the hairy ball theorem, Faber's approach ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) gives Coulomb interaction for them, 2) the simplest vortex loop resembles neutrino: stable - very difficult to interact with, 3 types: along one of 3 axes, can "oscillate" between them by internal rotation, are produced in beta decay, 3) loop with internal twist (hopfions?) might correspond to mesons, number of twists nicely fits strangeness - agrees with decay of mesons, strange baryons ( https://en.wikipedia.org/wiki/List_of_baryons ), 4) if another vortex goes through such loop, it nicely resembles baryons, interaction between its vortices creates charge inside (diagram below). Proton just closes this charge, while neutron has to compensate it - what is costly, explaining why neutron is heavier than proton (also quark-like fractional charge distribution), 5) combining baryons form nuclei as various size knots - binding them against Coulomb repulsion, including halo neutrons binded in much larger distance ( https://en.wikipedia.org/wiki/Halo_nucleus )

There is great book about topological solitons: http://www.lmpt.univ-tours.fr/~volkov/Manton-Sutcliffe.pdf Lots of talks: http://solitonsatwork.net/?display=archive

I am interested in solitons models of particles for more than a decade, some slides: https://www.dropbox.com/s/aj6tu93n04rcgra/soliton.pdf As particles, topological solitons can stay in place or travel - getting SR effects while approaching propagation speed, like Lorentz contraction, time dilation (e.g. for breathers), mass/momentum scaling. For example resting and traveling kink of this mechanical realization of sine-Gordon model:

Sure solitons can travel (e.g. getting Lorentz contraction), also nuclei (especially in LHC) - ideally we would like to recreate the space of possible particle, including their dynamics. For example we can recreate Coulomb interaction/Maxwell equations between topological charges: defining curvature of field of e.g. unitary vectors as EM field, Gauss law counts winding number/topological charge. Then using standard EM Lagrangian for this curvature leads to Maxwell equations - with built in charge quantization as topological (Faber's model https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) The question is how far we can go this way - which particles can be modeled as such "macroscopic quantum phenomena"? ps. Nice mechanical realization of 1D topological solitons - both moving and traveling, with pair creation/annihilation:

In any case, here are lots of interesting talks e.g. toward such models of nuclei: http://solitonsatwork.net/?display=archive Basic book: http://www.lmpt.univ-tours.fr/~volkov/Manton-Sutcliffe.pdf Some recent liquid crystal experimental paper: https://www.osapublishing.org/optica/fulltext.cfm?uri=optica-8-2-255&id=447762 Models of nuclei from https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.232002

studiot, I haven't met before with someone questioning energy of EM field alone - this is the energy in optical photon, power of radio transmitter, wireless charger, F_munu F^munu e.g. of QED, in derivation of Casimir effect, in 2.7K temperature of cosmic microwave background radiation, etc. But if you really deny energy of EM field alone, you can also use probe particle: Coulomb potential for electron + positron has V(r) ~ -1/r asymptotic behavior, what happens with it for r->0? Here is a diagram from classical Faber's model ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) : we model electric charge as topological charge of e.g. field of unitary vectors with Higgs potential V(u) = (|u|^2-1)^2 for regularization. Defining curvature of this field as electric field and using this standard F_munu F^munu Lagrangian (containing energy density), Gauss law becomes Gauss-Bonnet: counts winding number/topological charge - leading to Maxwell equations with built in charge quantization. So we take field configurations e.g. with two opposite charges in various distances, and calculate energy of this configuration: asymptotically he gets Coulomb, but it is deformed for very small distances (as in observed running coupling effect):

Photons are EM waves, antenna produces EM waves, wireless charger ... which carry energy proportional to |E|^2 without need for charged particles on the go.