Duda Jarek

@joigus, these are matters of interpretation, e.g. in perturbative QED interpretation Coulomb interaction is performed with photon exchange ... Should we really imagine some infinite sequence of exchanged photons e.g. between proton and electron in hydrogen atom? Or maybe should we remind that it is perturbtaive approximation - like expanding into Taylor series and representing terms of this series - where Feynman diagrams mathematically came from. In liquid crystal we get Coulomb-like long range interaction because the further e.g. opposite topological charges are, the larger total energy (stress) of the entire field is, e.g. with V(r) ~ 1/r behavior for Coulomb: In perturbative approximation you could get Taylor series and imagine it as photon exchanges, but this is just a different interpretation. So it is safer not to focus on interpretations first, but directly on particle behaviors like Coulomb interaction, decay modes - on agreement there first, then search for correspondence with perturbative QFT approximation of the Standard Model. What particle behavior you think is wrong in the framework I have presented? It also e.g. gets fractional charges in neutron ("quarks") - explaining why it is heavier than proton. Its topologically nontrivial vacuum requires Higgs-like potential corresponding to mass of particles - it allows to deform electromagnetism into other interactions in the center of particles - to avoid the infinite energy of electric charge issue.

I don't understand what do you mean by abstract space? E.g. sine-Gordon has mechanical realization as in the video, interaction between topological solitons is realized e.g. between fluxons in superconductors, long-range interaction is realized in liquid crystals (e.g. https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract ). This is about finding field and Lagrangian to get similarity with particles and fields - also the very real EM field. About repairing this very real EM field: that Gauss law in nature only returns integer charges ... what is done here by interpreting charge as topological, with Gauss-Bonnet theorem as Gauss law ... then the simplest nontrivial charge becomes a simple model of electron. This "biaxial nematic field" can be realized with a real symmetric tensor, exactly as stress-energy tensor in general relativity, by just using Higgs-like potential for it: preferring topologically nontrivial vacuum e.g. S^2, SO(3). But it is safer to be agnostic about its realization for this moment - first get the particles rights, then try to interpret the field e.g. with GR stress-energy tensor or some superfluid vacuum.

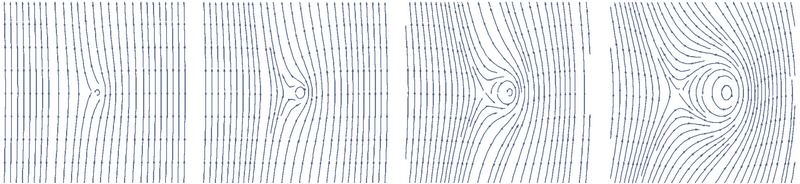
Sine-Gordon: just phi_tt = phi_xx - sin(phi) has already massive particles with quantized topological number, pair creation/annihilation, and entire special relativity: Lorentz contraction, time dilation, SR mass/momentum scaling ... studying this looking trivial toymodel is the best way I know to really feel the special relativity. Going to higher dimensions, here is example of observing long-range F~1/D force for topological solitons in liquid crystal: https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract We can choose dedicated Lagrangian to get exactly Coulomb interaction for them with included charge quantization as topological - e.g. Faber's way ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) : define EM field as curvature of some deeper vector field, this way Gauss law counts winding number - topological charge. But the goal is getting all the particles/interactions with dedicated field and Lagrangian - I have a framework, a sketch of Lagrangian, but getting the details + simulations was too difficult for me. Here is the sketch of this general framework again I would gladly discuss - for superfluid biaxial nematic field - of 3 distinguished axes: 1) we get 3 hedgehog realizations of one of 3 axes - kind of 3 leptons (the same charge, different energy/mass), with magnetic dipole due to the hairy ball theorem, Faber's approach gives Coulomb interaction for them, 2) the simplest vortex loop resembles neutrino: stable - very difficult to interact with, 3 types: along one of 3 axes, can "oscillate" between them by internal rotation, are produced in beta decay, 3) loop with internal twist (hopfions?) might correspond to mesons, number of twists nicely fits strangeness - agrees with decay of mesons, strange baryons ( https://en.wikipedia.org/wiki/List_of_baryons ), 4) if another vortex goes through such loop, it nicely resembles baryons, interaction between its vortices creates charge inside (diagram below). Proton just closes this charge, while neutron has to compensate it - what is costly, explaining why neutron is heavier than proton (also quark-like fractional charge distribution), 5) combining baryons form nuclei as various size knots - binding them against Coulomb repulsion, including halo neutrons binded in much larger distance ( https://en.wikipedia.org/wiki/Halo_nucleus )

This thread was supposed to be general as in title - about "Similarity between particle physics and macroscopic quantum phenomena like fluxons?" ... and sine-Gordon is just one of well established basic toymodels here.

But I have also sent you video of somebody's demonstration (e.g. https://www.youtube.com/watch?v=nl5Qq5kUbEE ) ... sine-Gordon is an old well established model: with varying number also of massive particles, behaving exactly as in special relativity ... in looking trivial model - just: phi_tt = phi_xx - sin(phi).

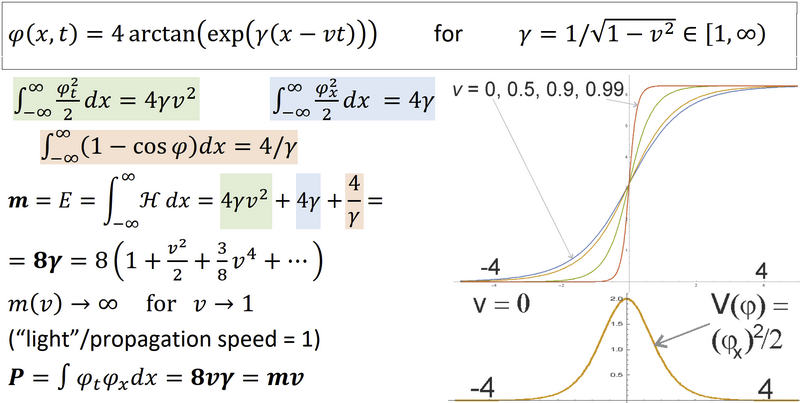
See e.g. the mechanical realizations of sine-Gordon - lattice of pendulums connected by a spring. Rotating them from one side, you get v=0 kink - going from one minimum of potential to the next one: rotated by 2pi. Here on slide 11 you have derived formulas, mass/momentum scaling as in SR: https://www.dropbox.com/s/aj6tu93n04rcgra/soliton.pdf

The "constant velocity" can be just v=0 ... especially that these are usually Lorentz-invariant models: allowing to change frame of reference to make the constant velocity zero. In this case, massive solitons scale mass/momentum exactly as in special relativity - they go to infinity while approaching propagation speed. See the sine-Gordon mentioned a few times, realized mechanically, or similar phi^4 - here is resting kink from https://en.wikipedia.org/wiki/Topological_defect#Images Here are initially two opposite topological charges traveling with constant velocities, which meet and annihilate - releasing mass (energy) as massless radiation (usually traveling at maximal - propagation speed):

The basic definition of soliton from https://en.wikipedia.org/wiki/Soliton is "In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity." For example with electron there comes E ~ 1/r^2 electric field, "while it propagates at a constant velocity" - doesn't it make electron formally a solitons? What more e.g. electron is than "sum of its fields"? Let me quote Einstein again from 1961 Infeld "Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta.": Regarding quantum effects for solitons, many are observed e.g. in superconductors/superfluids - I have started this thread with: There are also observed hydrodynamical analogues of many quantum phenomena, like Casimir, Aharonov-Bohm, orbit quantization etc. - gathered lots of papers: https://www.dropbox.com/s/kxvvhj0cnl1iqxr/Couder.pdf

ps. Very related: "Annihilation dynamics of topological defects induced by microparticles in nematic liquid crystals" - also long-range interactions (F ~1/D formula (1.2) below): https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract

Maybe let me briefly elaborate how I would hope to get all the particles from the biaxial nematic-like field (?), would gladly discuss: 1) we get 3 hedgehog realizations of one of 3 axes - kind of 3 leptons (the same charge, different energy/mass), with magnetic dipole due to the hairy ball theorem, Faber's approach ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) gives Coulomb interaction for them, 2) the simplest vortex loop resembles neutrino: stable - very difficult to interact with, 3 types: along one of 3 axes, can "oscillate" between them by internal rotation, are produced in beta decay, 3) loop with internal twist (hopfions?) might correspond to mesons, number of twists nicely fits strangeness - agrees with decay of mesons, strange baryons ( https://en.wikipedia.org/wiki/List_of_baryons ), 4) if another vortex goes through such loop, it nicely resembles baryons, interaction between its vortices creates charge inside (diagram below). Proton just closes this charge, while neutron has to compensate it - what is costly, explaining why neutron is heavier than proton (also quark-like fractional charge distribution), 5) combining baryons form nuclei as various size knots - binding them against Coulomb repulsion, including halo neutrons binded in much larger distance ( https://en.wikipedia.org/wiki/Halo_nucleus )

There is great book about topological solitons: http://www.lmpt.univ-tours.fr/~volkov/Manton-Sutcliffe.pdf Lots of talks: http://solitonsatwork.net/?display=archive

I am interested in solitons models of particles for more than a decade, some slides: https://www.dropbox.com/s/aj6tu93n04rcgra/soliton.pdf As particles, topological solitons can stay in place or travel - getting SR effects while approaching propagation speed, like Lorentz contraction, time dilation (e.g. for breathers), mass/momentum scaling. For example resting and traveling kink of this mechanical realization of sine-Gordon model:

Sure solitons can travel (e.g. getting Lorentz contraction), also nuclei (especially in LHC) - ideally we would like to recreate the space of possible particle, including their dynamics. For example we can recreate Coulomb interaction/Maxwell equations between topological charges: defining curvature of field of e.g. unitary vectors as EM field, Gauss law counts winding number/topological charge. Then using standard EM Lagrangian for this curvature leads to Maxwell equations - with built in charge quantization as topological (Faber's model https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) The question is how far we can go this way - which particles can be modeled as such "macroscopic quantum phenomena"? ps. Nice mechanical realization of 1D topological solitons - both moving and traveling, with pair creation/annihilation:

In any case, here are lots of interesting talks e.g. toward such models of nuclei: http://solitonsatwork.net/?display=archive Basic book: http://www.lmpt.univ-tours.fr/~volkov/Manton-Sutcliffe.pdf Some recent liquid crystal experimental paper: https://www.osapublishing.org/optica/fulltext.cfm?uri=optica-8-2-255&id=447762 Models of nuclei from https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.232002

studiot, I haven't met before with someone questioning energy of EM field alone - this is the energy in optical photon, power of radio transmitter, wireless charger, F_munu F^munu e.g. of QED, in derivation of Casimir effect, in 2.7K temperature of cosmic microwave background radiation, etc. But if you really deny energy of EM field alone, you can also use probe particle: Coulomb potential for electron + positron has V(r) ~ -1/r asymptotic behavior, what happens with it for r->0? Here is a diagram from classical Faber's model ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) : we model electric charge as topological charge of e.g. field of unitary vectors with Higgs potential V(u) = (|u|^2-1)^2 for regularization. Defining curvature of this field as electric field and using this standard F_munu F^munu Lagrangian (containing energy density), Gauss law becomes Gauss-Bonnet: counts winding number/topological charge - leading to Maxwell equations with built in charge quantization. So we take field configurations e.g. with two opposite charges in various distances, and calculate energy of this configuration: asymptotically he gets Coulomb, but it is deformed for very small distances (as in observed running coupling effect):

Photons are EM waves, antenna produces EM waves, wireless charger ... which carry energy proportional to |E|^2 without need for charged particles on the go.

Ok, you can skip r=0 case ... but such energy density should be continuous also there.

Regarding Heisenberg principle, notice that I am using "mean": what is mean energy density of electric field in distance r from electron? If one really needs a probe particle, e.g.: what is mean energy of electron - positron pair in distance r?

https://en.wikipedia.org/wiki/Electric_field#Energy_in_the_electric_field Or this F_munu F^munu in QED https://en.wikipedia.org/wiki/Quantum_electrodynamics#Mathematical_formulation

Regarding probing with other charged particle, there appears Coulomb potential V(r) ~ -1/r ... again having this infinity problem. There is scattering - extrapolating to energy of resting particles to remove Lorentz contraction contribution, we get ~100mb corresponding to size of electron in femtometers - we have discussed it here: But cannot we directly ask about field? Its mean energy density in r distance?

Ok, but in annihilation there are usually two (for para-positronium, +1 for ortho to reach zero angular momentum) ... e.g. used in PET imaging. Sure, in practice we need a bit larger energy to get pair in a distance ... ... but, this final energy also includes Coulomb potential V(r) ~ -1/r, again infinity in the beginning r=0 ... requiring some regularization. From one side, "subtracting infinity by hand" in renormalization is only mathematical trick - there still remains the question "what is mean energy density of electric field in distance r from electron?" Asymptotically ~|E|^2 = 1/r^4, but it leads to infinity - requires some deformation in the center. From the other, there are classical regularization methods. For example use Higgs potential V(u) = (|u|^2 -1)^2. It has |u|=1 vacuum (energy minimum), but e.g. in the center of topological singularity like hedgehog u(x) = x/|x|, to prevent discontinuity (infinite energy) it allows to get to v=0 by activating potential:

Energy conservation says that energy before and after should be the same. For 2gamma -> electron + positron pair creation: - energy before is 2x511keV in photons, which are EM waves - so this energy is initially in EM field, - energy after is, among others, energy of electric field of these two charges: integrating over energy density of E~1/r^2, we get infinite energy after this way. There is a problem, and just subtracting infinity in renormalization is only a mathematical trick without really understanding. We need to regularize this singularity: deform electric field to prevent E->infinity in the center. Running coupling ( https://en.wikipedia.org/wiki/Coupling_constant#Running_coupling ) can be seen as a consequence of such deformation: alpha increases e.g. to 1/127 in 90GeV - perfect point charges wouldn't need such deformation. Some discussion: https://physics.stackexchange.com/questions/386760/the-problem-of-infinite-energy-of-electron-as-point-charge Indeed the question of total energy of electric field of electron is extremely interesting - we only know the upper bound: 511keV. There are also other fields like magnetic of magnetic dipole: integrating energy density of all the fields, should we get 511keV or smaller? In other words: are particles more then just their fields? What more? Nice quote from 1961 Infeld "Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta.":

At least some of physicists believe in energy conservation, requiring source e.g. for hypothetical infinite energy. For example there is pair creation: of electron + positron from 2x511 keV only, so energy of electric field of such electron shouldn't exceed 511keV. But electric field of point charge is E~1/r^2, energy density is ~|E|^2, what integrates to infinite energy. So is there infinite energy in electric field of electron? QFT "repairs" this problem by just subtracting this infinity in renormalization procedure - successfully swept under the rug. But maybe it contains some regularization - deformation of electric field to indeed integrate to at most 511keV energy?

Especially in superconductors/superfluids there are observed so called macroscopic quantum phenomena ( https://en.wikipedia.org/wiki/Macroscopic_quantum_phenomena ) - stable constructs like fluxon/Abrikosov vortex quantizing magnetic field due to topological constraints (phase change along loop has to be multiplicity of 2pi). There is observed e.g. interference ( https://journals.aps.org/prb/abstract/10.1103/PhysRevB.85.094503 ), tunneling ( https://journals.aps.org/prb/pdf/10.1103/PhysRevB.56.14677 ), Aharonov-Bohm ( https://www.sciencedirect.com/science/article/pii/S0375960197003356 ) effects for these particle-like objects. It brings question if this similarity with particle physics could be taken further? How far? E.g. there is this famous Volovik's "The universe in helium droplet" book ( http://www.issp.ac.ru/ebooks/books/open/The_Universe_in_a_Helium_Droplet.pdf ). Maybe let us discuss it here - any interesting approaches? For example there are these biaxial nematic liquid crystals: of molecules with 3 distinguishable axes. We could build hedgehog configuration (topological charge) with one these 3 axes, additionally requiring magnetic-like singularity for second axis due to hairy-ball theorem ... doesn't it resemble 3 leptons: asymptotically the same charge (+magnetic dipole), but with different realization/mass?

Obviously many are coming, naturally selected especially for faster spread, now e.g. also from South Africa: https://www.cnbc.com/2021/01/06/south-africa-covid-strain-a-guide-to-what-you-need-to-know.html Again good interview: