Daedalus

Well, it's almost Thanksgiving. What do you have to be thankful for?

I agree with Strange. How do you define love Iwonderaboutthings? My definition for love does not require a belief in the human soul or a god. The Oxford dictionary defines love as: None of these definitions require a belief in a soul or in a god. Yes, I believe that you are confused. It's not that scientists don't have emotions, but that they have to remain unbiased in their opinions and feelings when conducting science in order to get to the truth of the matter.

I will give you rep and 5 stars 1 additional star if you can solve the problem, and you might get rep and stars from other people too. However, the biggest prize is the knowledge and satisfaction that you gain from working the problem and finding the solution, which is why I post these challenges. Of course, it also allows me to share problems that I have solved in a fun way instead of just posting a bunch of equations. Edit: Perhaps five stars is a little too much for solving one problem. I'll give you an extra star for each challenge that you win. By the time you have completed five challenges, you will have a vote of five stars and five points of rep from me. I realize it isn't much of a prize, but it's the best I can do. If I could offer more rep for solving certain challenges, I would. At least you will have gained some knowledge and bragging rights for being the first person to solve each challenge.

You're welcome!

John is absolutely correct. To continue with John's analysis, let's calculate the speed of the car as it goes over the edge of the cliff: [math]\frac{d}{dx}\left(5 t^2+\frac{65000}{3600}t\right)=10 t+\frac{65000}{3600}[/math] When [math]t=8/9\,\text{s}[/math], the car has traversed the [math]20\,\text{m}[/math] and is at the edge of the cliff with a speed in the postive [math]x[/math] direction equal to: [math]v=\left(10\,\frac{\text{m}}{\text{s}^2}\right)\left(\frac{8}{9}\,\text{s}\right)+\frac{65000}{3600}\,\frac{\text{m}}{\text{s}}=26.9444\,\frac{\text{m}}{\text{s}}[/math] Ignoring friction and air resistance, the only force exerted upon the car after it goes over the cliff is gravity. So, let's calculate the time it takes for the car to hit the ground: [math]y = -4.9\,\frac{\text{m}}{\text{s}^2}\,\,t^2+147.63\,\,\text{m}[/math] Setting [math]y=0[/math] and solving for [math]t[/math] we get: [math]0= -4.9\,\frac{\text{m}}{\text{s}^2}\,\,t^2+147.63\,\,\text{m}[/math] [math]t=5.48895 \,\,\text{s}[/math] As the car was falling, it was also moving in the positive [math]x[/math] direction with a speed of [math]26.9444\,\,\text{m/s}[/math]. Using this information along with the time it took for the car to hit the ground, we can calculate how far the car went in the positive [math]x[/math] direction: [math]\left(26.9444\,\frac{\text{m}}{\text{s}}\right)\left(5.48895 \,\,\text{s}\right)=147.896\,\,\text{m}[/math] The following image plots the path of the car:

I didn't use the derivative directly. Think about the other properties that tangent lines have besides being tangent to the curve. In other words, how can we use tangent lines to derive the parametric equation without using the derivative directly.

It has to work for any triangle, but it can help to work with a simple triangle to solve the problem. To give you all another hint, I solved the problem much like one would do for approximating an integral or for arc length. Hence, the use of the limit.

Now you are getting on the right track, and you already have two lines that are tangent to the parabolic curve. You should explore that method and see what you discover. Here, this should help you along: Point-Slope Linear Form [math]y-y_1=m(x-x_1)[/math] or [math]y=m(x-x_1)+y_1[/math]

A Beautiful Mind is a decent movie. Of course, there is Good Will Hunting, and Proof is ok.

I think you are heading in the wrong direction. Look further into what is going on in the problem. We clearly have two sides of the triangle that are tangent to the parabolic curve. To give you a hint, I had to use a limit. However, I didn't use the derivative directly. Instead, I used the tangents with a method I developed to solve this problem : ) I've never heard of anyone using this method before, but that doesn't mean it is new. Regardless, It's actually a pretty cool way to derive the parametric equation.

I appreciate the rep points, but is anyone interested in trying to solve the challenge? I do realize that it may seem complicated, but the answer can be derived using a few concepts from Calculus 1 and algebra.

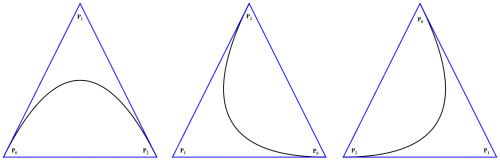
For this challenge, I've decided to go with the parabola yet again. If we take a triangle, it is possible to find three parabolic curves that fit perfectly inside the triangle such that two vertices of the triangle are located on a parabola with two sides of the triangle being tangent to the parabola at those points. The following image illustrates this property: The above image demonstrates these parabolic curves that fit perfectly in the triangle. Of course, the equation that describes the parabolas is not a standard function and is defined parametrically. Furthermore, the order of the points matter, which determines the parabolic curve and direction along the path. The goal of this challenge is to find the parametric equation that describes the parabolic curves that fit inside a triangle specified by the vertices [math]P_0=(x_0, y_0)[/math], [math]P_1=(x_1, y_1)[/math], and [math]P_2=(x_2, y_2)[/math].

I seen this one on FB and couldn't help but laugh...

It has been over two weeks and no one has provided the solution. So, here is the answer to this challenge: Ninth Challenge.zip

When it's not working, call tech support

Please disregard EdEarl's comment about trying to conduct this experiment yourself. It's not that EdEarl is wrong. You most certainly will fail. It's just that I'm concerned for your safety in dealing with anything explosive.

I call dibs on Ganymede. Can you imagine the view? It would be awesome.

Most definitely. I ended up converting from polar to parametric to derive the equation for the curvature because I like working with vector valued functions.

It seems to me that it would be easier for you to work in spherical coordinates. In the thread, Deriving formulae for spheres, I posted several equations for deriving properties of spheres. The equation for deriving a vector from the center of a sphere located at the origin to the surface of the sphere is [math]\text{V}\left(\rho,\,\varphi,\,\theta\right)=\left\langle\,\rho\,\text{sin}\,\varphi\,\text{cos}\,\theta,\,\,\rho\,\text{sin}\,\varphi\,\text{sin}\,\theta,\,\,\rho\,\text{cos}\,\varphi\,\right\rangle[/math] where [math]\rho[/math] is the radius [math]\left\{\rho\in\mathbb{R}\,|\,0\le\rho<\infty\right\}[/math], [math]\varphi[/math] is the inclination [math]\left\{\varphi\in\mathbb{R}\,|\,0\le\varphi\le \pi\right\}[/math], and [math]\theta[/math] is the azimuth [math]\left\{\theta\in\mathbb{R}\,|\,0\le\theta\le 2\pi\right\}[/math]. You can use the above equation to derive the vectors you need.

I'm not sure if you seen post #9, but I went ahead and gave everyone the name of the spiral to help speed things up. Yeah, there is quite a bit of information on the internet concerning logarithmic spirals, but oddly enough I haven't seen the equation for this particular derivation of the curvature. You will find other equations, but they are not in terms using only [math]d[/math] and [math]\phi[/math]. However, that doesn't mean you won't find it, but that it's not listed on the usual sites one would go to look. As for the case when [math]\phi = 90^\circ[/math], I included that in the graph I posted as a clue...

I never thought you went to a library. The comment was intended towards John's statement in the second post: It's ok to research the problem online, but one would still have to solve for the equation of the curvature in terms of [math]d[/math] and [math]\phi[/math], which is the whole point of the challenge.

That's actually pretty cool studiot. The professor who gave us this problem is a good friend of mine. However, he didn't want an equation for the answer. He gave us the distance [math]d[/math] and the angle of the moth [math]\phi[/math] with respect to radial lines from the center of the bug zapper and wanted the curvature of the logarithmic spiral at that point. So, as usual, I derived the equation and plugged in the numbers. It's actually a pretty neat problem with an interesting result once you try to solve it. I figured this challenge would be a nice break from my usual type of problems that can be tough to solve. Don't get me wrong. This problem can be challenging too. If you don't know the type of spiral, you would have to search for it online in order to get the equations, which was intended. I didn't expect anyone to go to a library and research the problem to solve it. However, the problem is no where near as tough as my other challenges.

Well, at least you're honest Unity Moontanman and I are friends, and I took his response as a joke. It's always hard to tell someone's intentions just through text. Feel free to solve the challenge. I found it quite interesting when I worked the problem many years ago, but I love mathematics.