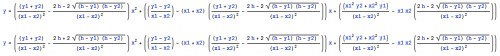Daedalus

Who actually gave neg rep to Moontanman? Don't worry I'll counter it...

The only way to know for sure Moontanman, would be to conduct a drug test on yourself and your wife to see if any drugs are in your system. Something like this test that you can buy at CVS: http://www.cvs.com/shop/product-detail/First-Check-Home-12-Drug-Test?skuId=346468

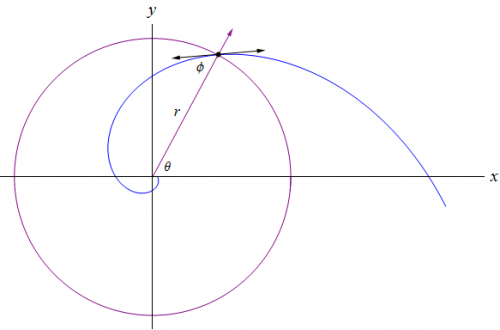
Lol... They sure don't. It's just a set up for the problem as was given to me by my Calc 3 professor. Just to speed things up a little, the spiral is known as a logarithmic or equiangular spiral.

True, it would be more fun, but the challenge only requires that one provides the equation for the curvature in terms of [math]d[/math] and [math]\phi[/math].

It's actually a clue that I provided hinting at the way I solved the problem. Nice attention to the details!

The problem has two parts. You have to know the type of spiral so you can get it's equation to find the curvature. The equation for it's curvature must be in terms of [math]d[/math] and [math]\phi[/math]. If you know the name of the spiral, go ahead and post it John. Perhaps someone will find the answer by googling it.

I was reminiscing about a problem that my Calculus 3 professor gave us, and decided to modify the problem to make it a little more challenging to solve. Although the problem isn't hard to figure out, it does have some interesting consequences. So without further adieu, I give you my ninth challenge. A Moth to a Flame It is common knowledge that certain insects, such as moths, are attracted to light sources. Let's consider that a moth navigates the world by maintaining a constant angle to the sun, which can be considered an infinite light source. Furthermore, let's say that at night the moth uses any light source that is available, and for all intents and purposes our light source is a bug zapper. Since the bug zapper is not an infinite light source, the moth will spiral into the bug zapper due to maintaining a constant angle with respect to radial lines from the center of the bug zapper that define the path of the spiral. The goal of this challenge is to identify the type of spiral, and to find the simplified equation for the curvature of the spiral in terms of the radial distance [math]d[/math] and the angle of the moth [math]\phi[/math] with respect to radial lines from the center of the bug zapper. Several clues have been given that should help you solve this challenge. Reputation awaits for the one who solves it first.

I'm referring to what you wrote earlier, which is wrong. The energy in 1 atom of Hydrogen is equal to the energy in 1 atom of hydrogen, and not 34.5 billion Hydrogen atoms worth of energy. What you wrote doesn't make sense.

Clearly you are misinterpreting the result. The energy of one Hydrogen atom is equal to the energy of one Hydrogen atom, and not 34.5 billion Hydrogen atoms. If you are comparing the value for the mass in kilograms (kg) to the value for the energy in joules (J), then you are comparing apples to oranges. The result of the comparison does not make sense unless you apply the conversion [math]c^2[/math] to the mass, which would make both sides of the equation equal to each other.

Try reading what you just wrote and see if it still makes sense. Now let's just narrow down the type of atom you are talking about to just a plain old, ordinary isotope of Hydrogen. Do you really think the energy contained in the mass of this Hydrogen atom equates to 34.5 billion Hydrogen atoms worth of energy?

The algorithm for nested roots in the first post is no longer being displayed properly by LaTeX. I am re-posting it so that everyone can see the algorithm again: Nested Roots: To find the nested root we must use the nested exponential function that has the constant as the nested exponent, [math]x^{\left\langle a\right\rangle}[/math]. Using this function with Newton's method yields the following algorithm for nested roots (Repeat the process until you have obtained the desired result): [math]\sqrt[\left\langle a\right\rangle]{b}[/math] [math]\text{approximated by}[/math] [math]x_{n+1}=x_{n}-\frac{\left(x_{n}\right)^{\left(x_{n}\right)^{(a-1)}}-b}{\left(x_{n}\right)^{\left(x_{n}\right)^{(a-1)}}\left(\left(x_{n}\right)^{(a-2)}\left(1+\left(a-1\right)\,\text{ln}\left(x\right)\right)\right)}[/math] Nested Logarithms: To find the nested logarithm we must use the nested exponential function that has the variable as thenested exponent, [math]a^{\left\langle x\right\rangle}[/math]. Using this function with Newton's method yields the following algorithm for nested logarithms (Repeat the process until you have obtained the desired result): [math]\text{nLog}_{\, a}\left(b\right)[/math] [math]\text{approximated by}[/math] [math]x_{n+1}=x_{n}-\frac{a^{a^{\left(x_{n}\right)-1}}-b}{a^{a^{\left(x_{n}\right)-1}}a^{\left(x_{n}\right)-1}\text{ln}\left(a\right)^2}[/math]

I'm not quite following what you are saying. Could you elaborate a little?

As part of the Wiener Process for the Cox-Zucker Machine, I have to get my Wiener Measure. Fact: The time-integral of the Wiener process results in integrated Brownian motion. So, don't forget Brownian motion before attempting butt coupling. Oh yeah!!! She knows how to work that ASS theorem.

You're welcome Amaton. I try really hard to make sure I come up with interesting challenges that invoke thought and are challenging. A lot of my challenges are actual problems that I have thought of and solved myself at one point in time or another. That is why you can't find them on the internet or in math books.

You're welcome To see how we use LaTeX, you can click on a formula and a pop-up will appear showing you the LaTeX. Basically, you enclose your equations with [ math ] [ \math ] tags (just remove the spaces in the tags. I had to add the space so that the forum will display the tags). You can also use the sandbox to test LaTeX expressions, and we have a tutorial on using LaTeX too. Good job on solving the challenge!!!

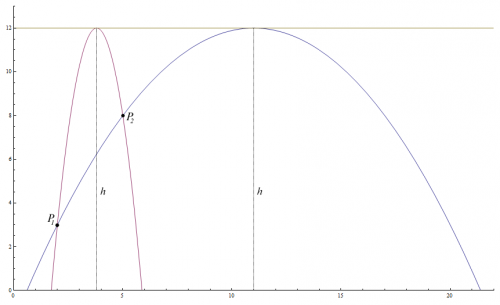
I was in the middle of editing my post when you replied. That caused the forum software to glitch and it messed up my edit lol. I do realize that writing the entire solution is a little bit of overkill, but that is the nature of solving these challenges. Nevertheless, here is how I solved the problem (Please note that there are several ways to arrive at the answer): Working The Problem To solve this problem, we write the equations for the parabolas using the specified points: [math]y_1=a\,{x_1}^2+b\,{x_1}+c[/math] [math]y_2=a\,{x_2}^2+b\,{x_2}+c[/math] Then, we solve for [math]c[/math] and set both equations equal to each other: [math]c=y_1-a\,{x_1}^2-b\,{x_1}[/math] [math]c=y_2-a\,{x_2}^2-b\,{x_2}[/math] [math]y_1-a\,{x_1}^2-b\,{x_1}=y_2-a\,{x_2}^2-b\,{x_2}[/math] Move like terms to one side or the other: [math]y_1-y_2-b\,{x_1}+b\,{x_2}=a\,{x_1}^2-a\,{x_2}^2[/math] Simplify both sides: [math](y_1-y_2)-b\,({x_1}-\,{x_2})=a\,({x_1}^2-\,{x_2}^2)[/math] Solve for [math]a[/math]: [math]a=\frac{(y_1-y_2)-b\,({x_1}-\,{x_2})}{({x_1}^2-\,{x_2}^2)}=\frac{(y_1-y_2)-b(x_1-x_2)}{(x_1-x_2)(x_1+x_2)}[/math] Expanding the result, we get: [math]a=\frac{(y_1-y_2)}{(x_1-x_2)}\frac{1}{(x_1+x_2)}-\frac{b}{(x_1+x_2)}[/math] That is when I noticed an interesting relationship between [math]a[/math], [math]b[/math], and the slope of the line that passes through the points, [math]P_1[/math] and [math]P_2[/math]. If we multiply both sides by [math](x_1+x_2)[/math] and then add [math]b[/math] to both sides we get: [math]a\,(x_1+x_2)+b=\frac{(y_1-y_2)}{(x_1-x_2)}[/math] This proves that the mid-point between the points, [math]P_1[/math] and [math]P_2[/math], on the parabola has a slope that is equal to the slope of the line that passes through [math]P_1[/math] and [math]P_2[/math]: [math]\frac{d}{dx}\ a\,x^2+b\,x+c=2a\,x+b[/math] [math]2a\,\left(\frac{x_1+x_2}{2}\right)+b=a\,(x_1+x_2)+b=\frac{(y_1-y_2)}{(x_1-x_2)}[/math] Getting Down to Business Now that we know [math]a=\frac{(y_1-y_2)-b\,({x_1}-\,{x_2})}{({x_1}^2-\,{x_2}^2)}[/math] we can solve for [math]b[/math]: [math]b=\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)[/math] Next, we can solve for [math]c[/math], which is really easy to do. All you have to remember is that the [math]y[/math] value of the vertex of the parabola is also the height [math]h[/math]. The vertex is defined as: [math]\left(-\frac{b}{2a},\ c-\frac{b^2}{4a}\right)[/math] Since our height [math]h[/math] is equal to the [math]y[/math] value of the vertex, we get: [math]h=c-\frac{b^2}{4a}[/math] or [math]c=h+\frac{b^2}{4a}[/math] Now that we have [math]b[/math] and [math]c[/math], we can solve for [math]a[/math]. First, we'll substitute the equation for [math]b[/math] into the equation for the parabola ( We can choose either point. I went with [math]P_1[/math] ): [math]y_1=a\, x_1^2 + \left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)\,x_1 + c[/math] Next, we substitute the equation for [math]b[/math] into the equation for [math]c[/math]: [math]c=h+\frac{\left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)^2}{4a}[/math] Then, we substitute the equation for [math]c[/math] into the equation for the parabola: [math]y_1=a\, x_1^2 + \left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)\,x_1 + \left(h+\frac{\left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)^2}{4a}\right)[/math] Deriving the Coefficients Finally, we have nothing but [math]a[/math]'s left along with the points and height. What you might not realize is that the variable [math]a[/math] is itself a quadratic equation. So, we must set it equal to zero. Thus, we have to subtract [math]y_1[/math] from both sides to get: [math]0=a\, x_1^2 + \left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)\,x_1 + \left(h+\frac{\left(\frac{(y_1-y_2)}{(x_1-x_2)}-a\,(x_1+x_2)\right)^2}{4a}-y_1\right)[/math] Now, once we simplify this god-awful mess, we get: [math]0=\frac{a^2\,(x_1-x_2)^4+2a\,(x_1-x_2)^2\,(2h-y_1-y_2)+(y_1-y_2)^2}{4a\,(x_1-x_2)^2}[/math] In order to make this a quadratic equation, we have to multiply both sides by [math]4a[/math] and distribute the denominator: [math]0=(x_1-x_2)^2\,a^2+(4\,h-2\,y_1-2\,y_2)\,a+\frac{(y_1-y_2)^2}{(x_1-x_2)^2}[/math] Because the equation for [math]a[/math] is a parabola itself, we have to use the quadratic formula to find the solutions: Quadratic formula (for our situation): [math]a=\frac{-B\pm \sqrt{B^2-4AC}}{2A}[/math] where [math]A=(x_1-x_2)^2[/math] [math]B=(4\,h-2\,y_1-2\,y_2)[/math] [math]C=\frac{(y_1-y_2)^2}{(x_1-x_2)^2}[/math] After working the quadratic formula and simplifying the result, we get: [math]a=\frac{(y_1+y_2-2\,h)\pm2\,\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}[/math] The Equations for A The above result is why there are two equations. Thus for [math]a[/math], we have: [math]a_1=\frac{(y_1+y_2)}{(x_1-x_2)^2}-\frac{2\,h-2\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}[/math] [math]a_2=\frac{(y_1+y_2)}{(x_1-x_2)^2}-\frac{2\,h+2\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}[/math] The Equations for B So, we must substitute both equations for [math]a[/math] into the equations for [math]b[/math] and [math]c[/math] in order to arrive at the solution. Substituting [math]a[/math] into the equation for [math]b[/math], we get: [math]b_1=\frac{(y_1-y_2)}{(x_1-x_2)}-(x_1+x_2)\left(\frac{(y_1+y_2)}{(x_1-x_2)^2}-\left(\frac{2\,h-2\,\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}\right)\right)[/math] [math]b_2=\frac{(y_1-y_2)}{(x_1-x_2)}-(x_1+x_2)\left(\frac{(y_1+y_2)}{(x_1-x_2)^2}-\left(\frac{2\,h+2\,\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}\right)\right)[/math] The Equations for C Finally, substituting [math]a[/math] and [math]b[/math] into the equation for [math]c[/math], we get: [math]c_1=\frac{({x_1}^2\,y_2+{x_2}^2\,y_1)}{(x_1-x_2)^2}-x_1\,x_2\left(\frac{2\,h-2\,\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}\right)[/math] [math]c_2=\frac{({x_1}^2\,y_2+{x_2}^2\,y_1)}{(x_1-x_2)^2}-x_1\,x_2\left(\frac{2\,h+2\,\sqrt{(h-y_1)(h-y_2)}}{(x_1-x_2)^2}\right)[/math] The Solution to the Challenge Now that we have [math]a[/math], [math]b[/math], and [math]c[/math] in terms of [math]\left(x_1,\,y_1\right)[/math], [math]\left(x_2,\,y_2\right)[/math], and [math]h[/math], we can put the pieces of the puzzle together and arrive at the solution for the challenge. We get [math]y=a_1\,x^2+b_1\,x+c_1[/math] and [math]y=a_2\,x^2+b_2\,x+c_2[/math] (Note: Latex can't handle equations this large. instead, I took a screen shot of the expanded form as displayed in Mathematica): However, no solution is complete without verifying the results. Therefore, we will check the vertex to make sure we are producing the correct results. Verifying the Result To calculate the coordinates for the vertex, we have to take the derivative of our functions and set them equal to zero and solve for [math]x[/math]: [math]x_{m1}=\frac{(x_1\,y_2+x_2\,y_2)-(x_1+x_2)\,\left(h-\sqrt{(h-y_1)(h-y_2)}\right)}{(y_1+y_2)-2\left(h-\sqrt{(h-y_1)(h-y_2)}\right)}[/math] [math]x_{m2}=\frac{(x_1\,y_2+x_2\,y_2)-(x_1+x_2)\,\left(h+\sqrt{(h-y_1)(h-y_2)}\right)}{(y_1+y_2)-2\left(h+\sqrt{(h-y_1)(h-y_2)}\right)}[/math] Now that we have the [math]x[/math] coordinates for the vertices, we plug them back into the equations for the parabolas and we get (verified with Mathematica): [math]f_1\left(x_{1}\right) = y_1[/math] [math]f_1\left(x_{2}\right) = y_2[/math] [math]f_1\left(x_{m1}\right) = h[/math] and for the second parabola (verified with Mathematica): [math]f_2\left(x_{1}\right) = y_1[/math] [math]f_2\left(x_{2}\right) = y_2[/math] [math]f_2\left(x_{m2}\right) = h[/math] Thus, we have proved / verified that the equations do indeed satisfy the conditions of the challenge as can be seen in the following graph: I have attached the Mathematica 7 file for this challenge to this post for those who want to see how I worked the problem. Enjoy!!! EighthChallenge.zip

Unfortunately, partial answers do not get you full credit. Although I use Mathematica now, I solved this problem a long time ago using a TI-89. So, I must insist that you provide a complete solution in order to get credit. I do check answers to ensure that they are correct.

It is a very difficult problem to solve. I'll give you another hint. The coordinate of the vertex is: [math]\left(-\frac{b}{2a},\ c-\frac{b^2}{4a}\right)[/math] Since we know that the height is equal to the [math]y[/math] value of the vertex, we get: [math]h=c-\frac{b^2}{4a}[/math] I hope that helps.

Sure np. It simply means that all axes as perpendicular or at right angles to each other. If you have every graphed a function in 2 dimensions, [math]x[/math] and [math]y[/math], then you might have noticed that the [math]x[/math] and [math]y[/math] axes are perpendicular / orthogonal / 90 degrees to each other. This is true for higher dimensional spaces too. Just look at 3D space. All axes, [math]x[/math], [math]y[/math], and [math]z[/math], are perpendicular / orthogonal / 90 degrees to each other. The same would hold true no matter how many dimensions of space there are. However, higher dimensions of space beyond three are not easy to visualize.

Well, it really depends on what we are talking about. The fifth dimension could be just another dimension of space. Such dimensions would be orthogonal (90 degrees) to every other spatial dimension (axes) no different than our 3 spatial dimensions and 1 temporal. However, any set of 5 variables creates a five-dimensional mathematical space. So, it doesn't neccessarily have to be spatial dimensions. If your question is related to physics, then I'll refer to Wikipedia - Five-Dimensional Space:

I always provide solutions whenever two weeks to a month have passed and the problem remains open, or when someone solves the challenge. However, I do provide hints to help you along the way. The first thing you should do is as follows: Write the parabolas using the given points: [math]y_1=a x_1^2+b x_1+c[/math] [math]y_2=a x_2^2+b x_2+c[/math] Next, you need to find a way to set them equal to each other so you can solve for [math]a[/math], [math]b[/math], and [math]c[/math].

Yes, you will end up with two parabolas where [math]a[/math], [math]b[/math], and [math]c[/math] will be in terms of [math]\{x_1, y_1\}[/math], [math]\{x_2, y_2\}[/math], and [math]h[/math]. However, both parabolas are actually a result of one equation, which is kind of obvious since both parabolas must pass through both points and reach a maximum height of [math]h[/math].

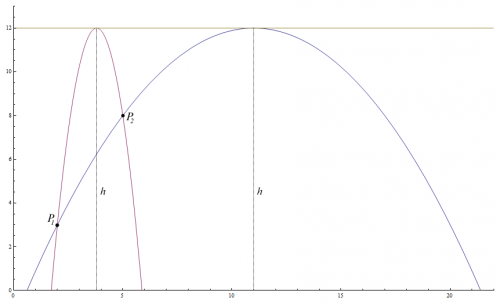
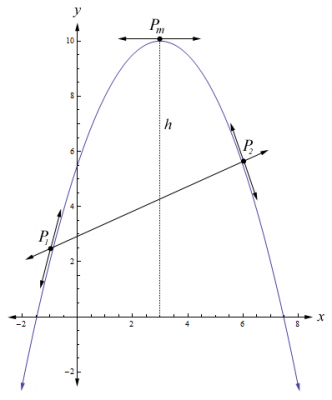
Despite the difficulty mentioned, I highly encourage anyone interested to try and solve this challenge. After all, it is based on parabolas and uses the quadratic formula. Thus, you only need algebra to solve it. Here is a graph that I have produced illustrating the problem, which should clarify the goals for the challenge. As you can see, both parabolas pass through the points, [math]P_1[/math] and [math]P_2[/math], and reach a maximum height of [math]h[/math].

No, the challenge is to find both parabolas that pass through the points, [math]P_1[/math] and [math]P_2[/math], and reach a maximum height of [math]h[/math]

For this challenge, I decided to go with something most everyone is familiar with, the parabola. Given that [math]y=a x^2 + b x + c[/math], the goal of this challenge is to find the parabolas that reach a height of [math]h[/math], and go through the points, [math]P_1=\{x_1,\ y_1\}[/math] and [math]P_2=\{x_2,\ y_2\}[/math]. All of the variables have been specified, and although this challenge may seem easy, I assure you that it is quite difficult. Reputation awaits the one who can provide the solution for this challenge first.