-
Posts
719 -
Joined
-
Last visited
-
Days Won
2
Content Type
Profiles
Forums
Events
Everything posted by Daedalus
-
Any takers? This one isn't too hard. Just a little tricky. It also has some interesting consequences.
-
Don't forget that you have to provide a single formula that works for any factor and value of [math]x[/math]. Not just powers of two. Just so there is no confusion as to what numbers your formula should generate, I am posting this image showing the exponents for factors of 2 through 8.
-
Thank you Phi for All
-
In my sixth challenge, which is based upon the Collatz conjecture, I found a way to determine the odd numbers that reduce to one given a count of the odd numbers within their Hailstone sequences. The reason why I focused my efforts on odd numbers is because all even numbers will reduce to an odd number by dividing it by two until an odd number is reached. As I was analyzing the sequence of exponents generated by recursively dividing even numbers by two, I noticed an interesting pattern and derived a formula to predict these exponents. Not only did I discover how to predict powers of two, but also for any other factor as well. The following image shows the exponents for factors of two, three, and four: As you can see, the first sequence is based on factors of two for the function [math]f(x)=2\,x[/math], the second sequence is based on factors of three for the function [math]f(x)=3\,x[/math], etc... Of course, the inputs and outputs are restricted to the set of integers. The challenge is to find a formula that predicts these exponent given the [math]x[/math] location and the factor. In other words, find the equation that predicts the values of [math]n[/math] given a factor [math]a[/math] and the variable [math]x[/math] for [math]\frac{a\, x}{a^n}[/math] Reputation awaits the one who can complete the challenge first.
-
I'm sure Phi for All did read what I wrote. He was just clarifying my explanation and emphasizing the finer points.
-
You're welcome
-
Well, it can be used to prove more complicated mathematical statements. As for science, math just predicts things and provides the means to model reality. As we make better measurements and observations, we are able to derive better mathematical models that make more accurate predictions.
-
You are confusing mathematics with science. In math, we can make statements such as theorems that can be proved. The Pythagorean theorem is one such example. Science uses math to construct theories, which can be falsified. Thus, math is a tool used by scientists to make quantitative predictions regarding the behaviour of physical phenomena.
-
How funny! All my life, people tell me I look like some famous actor or musician. I used to have really long hair, and when I wore my Lennon sunglasses, people said I looked like Ozzy. Without them, I used to get Dave Mustaine from Megadeath but with dark hair. Now that I've had short hair for over 15 years, people say I look like Charlie Sheen. Personally, I think they are all crazy... Perhaps, I should've tried to be an actor or a stunt double.
-
How to use the scientific method... http://youtu.be/LvkRUWk1kBE
-
It means I'm at a loss for words regarding your question. However, as stated in the rules, you are required to provide evidence to support your theory. Without evidence, this thread will be short lived.
-

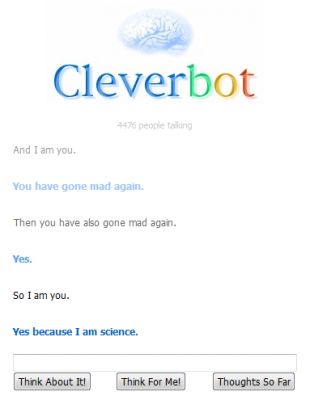
Fun game/puzzle: Stump the clever bot
Daedalus replied to EquisDeXD's topic in Brain Teasers and Puzzles
lol.... Me: You are talking to yourself. Bot: I am talking to you Me: And I am you Bot: You have gone mad again Me: Then you have also gone mad again Bot: yes Me: So I am you Bot: Yes because I am science hahahaha. rolfmao... -
Before I can answer any of these questions, I will have to derive the formula that will predict the equations. For instance, I still do not know the formula that predicts the count of the equations as the dimensionality increases, and I'm not sure if such approach will allow me to prove that all odd numbers are covered by these sets. As you are well aware, managing all of these equations becomes extremely difficult and it is easy for one to miss an equation within the set. However, since I do have a generalized formula for deriving such sets, the next step is to develop software that will iterate through each one and then develop a formula based on the results. To accomplish this, I actually use MathLink to invoke Mathematica within a C# application, which for me is easier than trying to program Mathematica itself. The two main patterns are skipping every other number [math]2\,x_0 - \text{offset}_0[/math] and [math]6\,x_i - \text{offset}_i[/math]. Once I am able to predict the offset for each index as the dimensionality grows, then I might be able to answer some of these questions.
-
Funny that you mentioned the Cytherian probe because I just watched that episode last night. It's one of my favorites. However, if I was Lieutenant Barclay, I would've had the computer record every single thought that came to me. I'm glad that you mentioned solving the pattern using brute force as well as provide your method for solving the challenge. Although I found a generalized algorithm that encompasses the problem set, I still had to resort to using brute force to find the patterns myself. It's important for an upcomming mathematician to understand that not all problems can be solved by manipulating equations alone. One must be able to search for patterns in a sea of numbers and variables, and to recognize the equations that predict how such patterns behave. Again, good job md65536!
-
I also heard the same things from my prof, which is why I applied the depth of analysis that I have done and continue to do. Although I was unable to prove the conjecture, I think the work I've done so far is absolutely awesome. Of course, I love everything mathematical and this conjecture yielded some unexpected results, which, as you know, is what us mathematicians live for and strive to achieve. To think that the dimensionality of the equations that predict these odd numbers approach infinity is a mind boggling result. Not to mention that the number of equations also increase. Furthermore, the equations that predict these odd numbers include the equations for the previous odd numbers. This means that if you could somehow take this process to infinity, not only would you have equations with infinite dimensions, but also that there would be an infinite number of such equations. Truly an amazing result! Moth, I commend your efforts and give you props. Thanks for the rep. It truly feels like a pat on the back. Although this problem was beyond your current level of mathematical skill, I do hope that you were able to take from this challenge and increase your level of understanding on how we attack these type of problems. Just remember that everything you have ever learned in math is just another puzzle piece in the big picture. As you tackle and solve mathematical problems, you gain new puzzle pieces that can help you solve the next problem. Even if you fail to solve a problem, you can still gain valuable insights into mathematics by just making the attempt.
-
When I first started working on trying to prove the Collatz conjecture I noticed that every single even number will reduce to an odd number, and that even numbers of the form [math]2^x[/math] will reduce to one without incurring another odd number in the Hailstone sequence. So the first thing I did was to set [math]3\,m+1=2^n[/math] Solving for [math]m[/math] we get [math]m=\frac{2^n-1}{3}[/math] However, not all values of [math]n[/math] produce odd numbers. Instead, every other number is odd with the rest being rational numbers as shown in the following image: As we can see, every other number produces an odd number. Thus, we have the first pattern in the form of skipping every other number, and arrive at the equation for all of the odd numbers that reduces to one which have two odd numbers in their Hailstone sequence: [math]m=\frac{2^{2\,n}-1}{3}[/math] It became obvious that if the conjecture was true, then all other odd numbers must eventually reduce to one of the values of [math]m[/math], which would then reduce to 1. I realized that I could repeat the process, but that I would have to add a new dimension for each [math]2^x[/math] that was nested. Thus, I arrived at the following generalization: Every single odd number that reduces to one is determined by the above generalization. However, the challenge is now finding the equations for the indices of each dimension. By analyzing the equation for 3 odd numbers, I was able to find the second and final pattern (the one that generates the [math]6\,x + \text{offset}[/math] for the remaining variables): You can see that rows 2, 4, 8, 10, 14, 16, etc... all have odd numbers that reduce to one of the numbers in the first equation. However, it's easier to write an equation for 2, 8, 14, etc... and one for 4, 10, 16, etc... This produces the following equations for the indices: [math]6\,x-4[/math] [math]6\,x-2[/math] This is why there are two equations for 3 odd numbers: The above image shows us why we either have to skip every other number by [math]2\,x[/math] or [math]2\,x-1[/math], which further complicates the problem. However, the rest of the indices are of the form [math]6\,x-\text{offset}[/math]. I've checked this for 4 and 5 odd numbers in the sequence and it is holding true. You might have noticed that we got back the equation for two odd numbers in the Hailstone sequence in our solutions for three odd numbers in the Hailstone sequence. Although this may seem odd, you have to remember that Hailstone sequences are cyclic when they reach one. This is because if you plug 1 back into the formula, you will get back 1 again. Now for the most interesting thing of all. You would think that the odd numbers that have three odd numbers in their Hailstone sequence would reduce to one of the odd numbers that have two odd numbers in their Hailstone sequence and that you would get back the entire set of numbers. However, this isn't the case. It turns out that there are odd numbers that have two odd numbers in their Hailstone sequence that do not branch to an odd number that has three odd numbers in its sequence. I discovered this fact when I applied the Collatz formula to the odd numbers that have three odd numbers in its sequence to produce: As you can see, these odd numbers do not reduce to every odd number that has two odd numbers in their Hailstone sequence. In other words, the numbers 21, 1365, 87381, etc... do not branch to an odd number that has 3 odd numbers in its sequence. In fact, any odd number that has two odd numbers in its Hailstone sequence and is a multiple of 3 will not branch to an odd number that has 3 odd numbers in its Hailstone sequence. I propose that such numbers terminate that branch and will not produce another odd number in the sequence. I have attached a zipped Mathematica 7 file containing the work I've done thus far to this post for anyone who wishes to work with me or explore the problem for yourself. All I ask is that if you do manage to prove the conjecture using my work, that you give credit where it is due Collatz.zip
-
Good job md65536, you provided the correct solutions and won the challenge earning you rep and 5 stars from me : )
-
Md65536, I'll check your equations when I get home tonight. At first glance, they seem to be correct. If so, then i'll post the usual breakdown and explanation of the solution. There are two main patterns that are expressed for the indices with some interesting consequences as a result. Although it might be possible to massage these equations into one, it will be extremely difficult because the number of equations increase nonlinearly as the number of odd numbers in the Hailstone sequence increases.
-
I checked your equations earlier and they produced the correct results. I'm not concerned with indices being offset as long as the equations produce the correct sequences. As for the missing equation for 3 odd numbers, the pattern is a little more complex. I'm on my phone right now, but when I get home tonight I will post a sequence that the equation you posted for 3 odd numbers doesn't predict. In other words, not only do the dimensions increase as there are more odd numbers in the Hailstone sequence, but also the number of equations too. As for an example number, it's either 13 or 113. Both have 3 odd numbers, but since I'm not home I can't check which one belongs to the missing equation.
-
Almost there md65536. Although your equations are correct, you are missing an equation for 3 odd numbers in the Hailstone sequence. Thus, the solution for 3 odd numbers requires 2 functions.
-
Moth, those results look a lot better than the outputs you posted previously. As for solving the challenge, try to find the equation for the odd numbers that only have two odd numbers in their Hailstone sequence. Once you have done that, then the next part becomes obvious but still challenging.
-
Moth I don't think your program is producing the correct results. Check the output with a known Hailstone sequence. I would check it for you, but I'm at work. However, this challenge requires both algebra and analytic methods to find the solutions.
-
Yeah, the equation for two odd numbers is easy to find once you realize what happens to the even numbers. Three odd numbers in the Hailstone sequence is a bit more challenging ; )
-
Anyone going to try to figure this one out?