Daedalus

If you truly want to become a software engineer, then I say go for it!!! Not only will you be able to use your abilities in mathematics, but also the pay isn't bad either. Plus it doesn't hurt having already been disciplined and exposed to criticism as a ballerina. Although being a ballerina isn't the same as a software engineer, you will find that you will refer back to that training when dealing with such stressful environments. I know being a musician and a mathematician has helped me tremendously because I can take the pressure / criticism as well as figure things out much easier, which translates into my career more than you would imagine. Oh... and welcome to the Science Forums. I hope you find this site as enjoyable as I do. If you need any help, don't be afraid to ask me or any of our mods / experts

Most companies require you to have a Bachelor of Software Engineering (B.SE) or related degree before they will hire you. However, that isn't necessarily true as I have worked for companies that care more about experience than which degree you have. As for going for a masters degree, it can help if you want to go for a management position such as being a Project Manager, Director of Engineering, etc... However, you will still need to have sufficient experience before you will be able to get that type of position. As for getting a software engineering position while going to graduate school, you might be able to land an internship. However, you have to realize that software engineering can demand a lot of a person's time. Now let's talk about the job because even though I find it as enjoyable as you do, it's not entirely all fun and games. Software engineers not only have to be able to develop their part of the program, but also be able to work in a stressful environment where you have to meet the expected deadlines and be able to deal with any problems that might arise within the code base. It really isn't a job for the weak at heart. I've had my ass chewed because the owner(s) of the company found a glitch in the games, but then I've also been awarded to a nice dinner or trip to Vegas for fixing such bugs in a timely manner. I'm not trying to discourage you from becoming a software engineer. I only want you to be aware that, even though we love the job, it really can be a pain in the arse. Plus, you will need to work on your math skills so that you can create algorithms that you would otherwise not be able to without the math. In closing, I have over 12 years experience in the industry, and I must say that the good outweighs the bad. I even got to meet Drew Carey and Pamela Anderson at G2E (worlds largest casino gaming expo) in Las Vegas, and they even autographed my badge. So if you don't mind a lot of hard work, getting chewed out, and having to deal with extremely stressful situations, then by all means I encourage you to pursue the career path.

That's not necessarily true as it depends on the coordinate system you are working with. For instance, when dealing with double integrals, we normally work with rectangular coordinates where [math]dA = dx\,dy[/math]. However, when dealing with polar coordinates we find the transformation from rectangular to polar involves [math]dA = r\,dr\,d\theta[/math]. This gives us the following relationship: Of course, we can integrate a function in any coordinate system by using a change of variables. This gives us a generalized method, which can be easily extended to triple integrals, that makes it easier to work in different coordinate systems such as spherical coordinates. If we use the equation for a circle, we can confirm that the Jacobian of the polar to rectangular transformation yields [math]\left|J(u,v)\right|dA=r\,dr\,d\theta[/math]: [math]T:\,\,\,\,x=g(r,\theta)=r\,\text{cos}\,\theta,\,\,\,y=h(r,\theta)=r\,\text{sin}\,\theta[/math] [math]J(u,v)=\frac{\partial(x,y)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}=\begin{vmatrix}\text{cos}\,\theta&-r\,\text{sin}\,\theta\\\text{sin}\,\theta&r\,\text{cos}\,\theta\end{vmatrix}=r(\text{cos}^2\,\theta+\text{sin}^2\,\theta)=r[/math] Thus giving us [math]dA=r\,dr\,d\theta[/math]. Now if we let [math]f(x,y)=1[/math], then we can derive the area of a circle using our new found knowledge by setting [math]\alpha=0,\,\beta=2\pi,\,a=0,\,\text{and}\,b=r[/math]: [math]\int_{0}^{2\pi}\int_{0}^{r} r\,dr\,d\theta=\int_{0}^{2\pi}\frac{r^2}{2}\,\,d\theta=\pi\,r^2[/math] The above example translates directly into finding the area of polar regions The reason why I introduced this into the discussion is because, when dealing with spheres, it is much easier to work in spherical coordinates where [math]x=\rho\,\text{sin}\,\varphi\,\text{cos}\,\theta[/math] [math]y=\rho\,\text{sin}\,\varphi\,\text{sin}\,\theta[/math] [math]z=\rho\,\text{cos}\,\varphi[/math] [math]\rho[/math] is the radius where [math]0\le\rho<\infty[/math] [math]\varphi[/math] is the colatitude where [math]0\le\varphi\le\pi[/math] [math]\theta[/math] is the polar angle where [math]0\le\theta\le 2\pi[/math] Note: Physicist may reverse the role of [math]\varphi[/math] and [math]\theta[/math] - "Calculus Early Transcendentals - Briggs & Cochran" (pg 924) Also because this line of thinking might give you some new insights on deriving formulas for spheres. Now let's compute the Jacobian for the equation of our sphere so that we can derive the equation for it's volume. [math]J(u,v,w)=\frac{\partial(x,y,z)}{\partial(u,v,w)}=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}&\frac{\partial x}{\partial w}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}&\frac{\partial y}{\partial w}\\\frac{\partial z}{\partial u}&\frac{\partial z}{\partial v}&\frac{\partial z}{\partial w}\end{vmatrix}=\begin{vmatrix}\text{sin}\,\varphi\,\text{cos}\,\theta&\rho\,\text{cos}\,\varphi\,\text{cos}\,\theta&-\rho\,\text{sin}\,\varphi\,\text{sin}\,\theta\\\text{sin}\,\varphi\,\text{sin}\,\theta&\rho\,\text{cos}\,\varphi\,\text{sin}\,\theta&\rho\,\text{sin}\,\varphi\,\text{cos}\,\theta\\\text{cos}\,\varphi&-\rho\,\text{sin}\,\varphi&0\end{vmatrix}=\rho^2\,\text{sin}\,\varphi[/math] This give us the relationship that [math]dV[/math], which in rectangular coordinates is equal to [math]dx\,dy\,dz[/math], is equal to [math]dV=\rho^2\,\text{sin}\,\varphi\,d\rho\,d\varphi\,d\theta[/math] in spherical coordinates. This allows us to find volumes in spherical coordinates by using triple integrals. If we let [math]f(\rho,\varphi,\theta)=1[/math], then we can derive the formula for the volume of a sphere: [math]\int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{r}\rho^2\,\text{sin}\,\varphi\,d\rho\,d\varphi\,d\theta=\int_{0}^{2\pi}\int_{0}^{\pi}\frac{1}{3}r^3\,\text{sin}\,\varphi\,d\varphi\,d\theta=\int_{0}^{2\pi}\frac{2}{3}\,r^3\,d\theta=\frac{4}{3}\pi\,r^3[/math] Furthermore, we can derive the surface area of the sphere by modifying the above integral such that we no longer integrate along the radius. We'll also use [math]r[/math] instead of [math]\rho[/math]: [math]\int_{0}^{2\pi}\int_{0}^{\pi}r^2\,\text{sin}\,\varphi\,d\varphi\,d\theta=\int_{0}^{2\pi}2\,r^2\,d\theta=4\,\pi\,r^2[/math] Although this post might not be along the same line as what you intended, I do hope that this information proves helpful in deriving formulas for spheres

Hehehe... Thanks for the complement, but I encourage you to only use the original melody in your arrangement of the music. Although I wouldn't mind you using my work for non commercial use, it doesn't really help you discover a new and unique arrangement based on your interpretation of the original work. Creating your own arrangement is an exercise that will help you progress as a musician, and helps build upon your existing knowledge of music theory and composition. However, you could use the rythmic structure of my music to see if you can find different harmonies and melodic lines that create a different feel. It would still be a derivative work, but that would also be a good exercise into understanding how I used these structures to create the music. My goal for this composition was not only to build upon the original work, but also leave the orignal melody intact so that anyone who knows the original tune will be able to recognize it within my own work.

Thanks for the complements. *takes a bow* After speaking with my father, who is a bluegrass fiddle player and somewhat of an authority on folk music, I made two changes. He suggested changing the original melody in the seventh measure to fit better with the music of the violin, and that I should change the tempo from Allegretto (100 BPM) to Allegro (110 BPM). He also reminded me to file my copyright. So I did as he suggested, and as most always when it comes to music, dad was right : ) The seventh measure of the melody, which occurs about 7 seconds and 34 seconds into the song, is melodically and harmonically correct. However, it was a little lacking rhythmically in how it relates to the violin music. So instead of playing four 8th notes, I removed the last note and replaced it with two 16th notes. The tempo change, although very slight, allows the 16th notes in the violin music to progress more smoothly. While this may seem like nitpicking, to a musician it can make a difference. Of course, it really is a matter of opinion, but I personally like the changes and I hope everyone else does as well. Here is the the for those who do not wish to download the .mp3 file: I noticed that the video renders over the picture of the sheet music when you click to view it. To solve the problem, I have posted it here (edit: It seems that you have to scroll down far enough so that the video is no longer on the screen. Then, you can click the image of the sheet music to view it without the video rendering on top of it): Due to the success in arranging the music for this song, I've decided to take other folk songs and repeat the process. Once I have enough songs for an album, I will upload the music to youtube and post it in my thread, Music Theory and Composition, for everyone to enjoy. A casa d'un drapaire.mp3

Well... I think I have finally completed this composition, and I have to say, I think it is my best one yet As before, here is the the for those who do not wish to download the .mp3 file: I hope everyone enjoyed the journey as much as I did!!! A casa d'un drapaire (final).mp3

To be fair, I have been playing and writing music for over 22 years. In addition, I come from a very long line of musicians on my father's side of the family. My father plays bluegrass on the fiddle / violin, my cousins play violin, my aunt and uncle play piano, my grandfather played violin for the Detroit Philharmonic, my brother plays guitar, and I play guitar and piano. I was also the president of the honor choir in high school, which does wonders for tuning ones ear and helps me play / write the music I hear in my head. Furthermore, I studied many of the greats such as Bach, which also helps one to develop an understanding of the theory. So, I guess you could consider me to be a Maestro because I also teach music, especially to my sons (have to keep the family tradition going) As for the music feeling a little incomplete, I will build up the composition as I find time to do so. It's just one of those things I love to do : ) I find that's not entirely true. It really depends on one's ability to hear other harmonies and melodies that would fit the music. Whether you create an original piece of music or make an arrangement of someone else's music, it's really the same process.

Actually, I could analyze the music if I really wanted to ; ) I can get the notes either by using software or just by listening to the music. As for the piece of music being discussed, I really can't stand synthesized strings. They just don't sound quite right. However, I rendered the music for clavinet / piano, and made a much better recording by tweaking some settings in Pro Tools. I still haven't finished the toccata because I've been spending time with my kids. So, without further adieu, I give you a more folksy sounding recording: If you do not want to download the attached .mp3, I have uploaded a video, including the sheet music, to . Furthermore, Externet was kind enough to translate the lyrics for me. Given the comical nature of the words, I couldn't resist reposting it here: A casa d'un drapaire (clavinet).mp3

Thank you zapatos. It has taken me about six hours to arrange the accompaniment, and the toccata is comming along nicely : ) I've modified the main melody to transition with the harmony in a much more pleasant way. The modification is located in the 9th measure (9 seconds into the song) where the instruments used to play the same chord throughout the whole measure. This made the transition to the 10th measure seem unnatural. However, the modification allows the song to flow nicely ; ) I will finish the toccata tomorrow. If anyone wants the music to this version of the song, I had Pro Tools save the sheet music and have posted it below. Enjoy!!! A casa d'un drapaire (revised).mp3

Thank you. I appreciate the opportunity to be able to transform this piece of music into a modern work of art. Once I get the toccata for it written, I will post it ; )

You haven't heard the string quartet version I'm writing for you ; ) I don't mean to brag, but the harmonies I'm writing for it are awesome. I'll post it here in about 10 - 15 mins. Then, I will continue to write more harmonies for it because it is such a beautiful piece of music!!! Here is the string quartet version that I wrote: A casa d'un drapaire (string quartet).mp3

Ok... I have recorded the main melody with Pro Tools using the sound of a grand piano. I will analyze the music and create some harmonies for it so it will have an accompaniment to support the melody. I am wondering if you also want the second song from Cancons tradicionals a Mont-roig del Camp? A casa d'un drapaire.mp3

When I get back from taking my boys swimming I will make a recording for you. In the meantime, you can enjoy some of the music I've written and have posted here: http://www.scienceforums.net/topic/58404-music-theory-and-composition/ There isn't a key change. The B flat is just an accidental. All of the Bs in that measure remain flat, but only for that measure. Afterwards, the Bs go back to the key of C major / A minor.

No that's just not true. I used OpenGL (without GLM) along with DirectX when I created a proprietary cross-platform game engine for Casino Systems Inc. Of course, GLM does provide all those handy matrix functions that work on vectors / vertices, but it is not a requirement (especially if the code base already has functions to do this). md65536++ ; ) Exactly and I can't stress md65536's statement enough!!! Please, do not try to reinvent the wheel. If you do not know what you are doing, it will cause you nothing but headaches. You will appreciate this statement when or if you already have had to come in behind someone to fix their crappy spaghetti code because they considered themselves to be a coding god (only to find out that they have never designed or implemented a game engine in their life). For a decent graphics engine, I recommend using OGRE, which is used by Multimedia Games in their latest game engine, or SDL, which is also cross-platform.

I'm sure most of you know that we had another outbreak of tornadoes on May 31, 2013. The numbers are finally in and channel 9 has reported that the tornado that hit El Reno was a record breaking 2.6 miles wide with winds of 295 mph. NBC news also reports the same. Luckily, I was in Norman, OK at the time and took shelter at Norman Regional Hospital. They have underground facilities, and are equipped to handle such emergencies. However, veteran storm chaser, Tim Samaras, his son Paul, and thier collegue Carl Young were killed during the storm when the tornado turned and struck their vehicle. With 13 people confirmed dead from this latest storm, May 2013 was a deadly month for Oklahoma with two confirmed EF5 tornadoes within a two week period.

I'll defer to your expertise. I'm definitely not an expert on construction materials or techniques beyond building cabinets. I agree with you 100%. I never thought it was a good idea to have students simply go into a bathroom or hallway during a tornado.

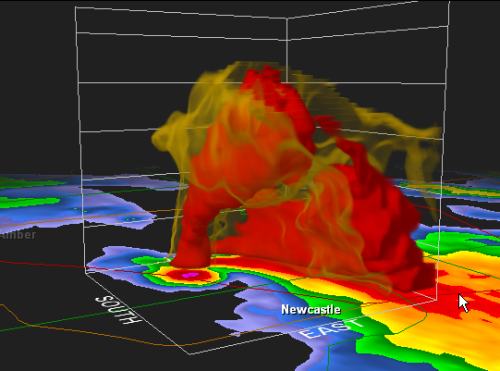
The May 20, 2013 tornado that hit Moore, Ok has been upgraded to an EF5: http://www.weather.com/news/tornado-central/tornado-f5-ef5-rarity-20130521 The death toll has also been revised. Fortunately it went from 51 to 24. However, 9 children are included amongst the dead, including a 3 month old baby and it's parents :' ( http://abcnews.go.com/US/oklahoma-tornado-kills-51-including-20-children-death/story?id=19222656 Here is a link with some very heart breaking photos of the destruction :' ( http://tv.msnbc.com/2013/05/21/photos-oklahoma-after-the-tornado/ The following two photos should let you know why concrete structures provide little protection again an EF5 tornado: We can see the rebar protruding from the concrete in this photo: Of course, as Michel123456 has pointed out, wood structures provide even less protection: Here is a pic of the storm as seen from space. The red line is the path of the tornado: http://www.universetoday.com/102282/oklahoma-tornado-on-may-20-2013-as-seen-from-space/ Here's a cool 3D image of the tornado right as it was crossing I-44. Newcastle, OK is about 9 miles southwest of Moore, OK:

No they are actually shouting due to being deaf from years of rocket launches... You know... The rockets they launched at the sun to celebrate the X games.

It looks more like a Japanese / Chinese symbol. Perhaps it means gullible in Mandarin...

I have seen the dome and underground homes here in Oklahoma. I imagine the dome would survive better than traditional homes, but I do not have any data to support that claim other than the fact that debri has a better chance of being deflected by the dome versus a vertical wall. I am not sure how they would hold up against a F5 considering that during the May 3, 1999 tornado Gary England told us to flee our homes or we would not survive. This has more to do with the size of an F5 tornado in that they can be anywhere from 1 - 2 miles wide if not wider.

Thanks for all the condolences. Having been in a tornado (in a cellar) and near several of them, I appreciate all the comments. We have building codes and regulations, but you have to remember tornadoes, at least F4s and F5s, have no problem leveling reinforced concrete structures. Just look at the last pic in post #4. That is a school that, by law, is built with such reinforcement. The problem is that it's not the wind that destroys the homes per say, but what the wind is blowing. The funnel pretty much can pick up almost anything, even semi-trucks and other houses, and slam it into buildings. Just imagine being in a reinforced concrete structure that is being slammed by pieces of reinforced concrete structures and hoping that your building can hold up to the abuse. So, it's mainly the debris ball that destroys other structures. We even build reinforced concrete structures, safe rooms, inside homes of all types, especially wooden ones. However, the only truly safe place during a tornado is underground in a reinforced concrete cellar with a steel door that latches / locks down from the inside. I would like to point out that the government does, in fact, help with the cost of safe rooms and cellars. We also have public cellars in areas, such as trailer parks, that do not have cellars or safe rooms. Also, I'm not aware of any schools in Oklahoma that are built next to fertilizer or oil and gas plants, but you never know.

Here are some pictures that my friends, family, and local news stations are posting on FB :' (