Daedalus

It has been a while since I've released a new song, but I'm happy to share a collaboration between myself and my very talented friend, Dean Rockholt. Dean came up with the melody, and the guitar and drum parts. I then added the strings and extended the melody by giving it fills and changing a few notes, but Dean's original melody is still intact. As some of you know, I lived in North Carolina for a few years, which is where I met Dean and his family. This song, North Carolina Nights, is dedicated to all of my friends and family living in North Carolina. Enjoy!!!

Moontanman, that reminded me of Bo Burnham's song, "From God's Perspective - You're Not Going to Heaven". ROFL!!!

Instead of dealing with real valued functions such as wave harmonics, why not try an integer based approach. In my Seventh Challenge, I post a function that completely maps out the factors for any number. Perhaps you can use the equations.

Umm. Sorry, that would be "Rick and Morty"

Thanks Koti, that thing will haunt my nightmares till I die...

Of course there are fans here! Go House Targaryen and House Stark!!!

The LHCb team stated yesterday that it "is charmed to announce observation of a new particle with two heavy quarks". The paper describing the discovery can be found here: https://press.cern/sites/press.web.cern.ch/files/file/press/2017/07/lhcb_paper_2017.07.06.pdf

I knew I should've replied...

Unfortunately Dr. Richard, you are really bad at explaining you're ideas. I don't mean to insult you (well... maybe just a little for being a dick), but it took 3 pages of posts for you to finally tell us that you have an idea where you relate numbers to words, or "representations of a language" as you like to call it, that allow you to provide a key or "index" to a dictionary of definitions. As Strange has clearly stated, this is nothing new and is definitely an incomplete system for translating one language to another. Even if the translation of a language into another is not what you intended, the software that runs any online dictionary surely already does what you are implying. As a software engineer, I would create a Dictionary<string, string> Definitions {get;set;} property that relates a word to it's definition or description of how it's used in the language such as the articles a, an and the in the English language. Because all computers work entirely using numbers, the characters or symbols from any language can be and most likely are defined by Unicode, which is a numerical system that allows a computer to display words using the font that provides the symbols for a particular language. However, that alone isn't enough to translate from one language to another. Furthermore, how does assigning numbers to words help you understand reality? When most people talk about understanding reality, they are referring to physics. Language is nothing more than a way of recording, processing, and sharing information where understanding reality requires application of the scientific method. So, the title of this thread is highly misleading.

I'm not quite sure what you are asking because I don't know what epura means (graph?) and Google didn't provide a decent translation. Can you be more specific?

If you truly want to understand mathematics as I understand it, then I'd be more than happy to instruct you in the ways of the force. However, I'm not a professor, but I do tutor people for free and am more than happy to help. A few years ago, before I found a job as the Sr. Software Engineer for Factor, I tutored several people taking Calculus 1 - 3 at Oklahoma City Community College. I was able to help several students understand calculus better and improve their grade because I absolutely love math and have a knack for identifying where someone is struggling, relate the mathematics in way they are familiar with, and help them overcome the problems they are having. So, you can always send me a PM and I'll do my best to help, or you can post your questions here in the math forum because there are plenty of people who are also happy to help and are more knowledgeable than I. Of course I did. The mathematics that I included in the post are based on real events and actual problems that I solved for myself or in the process of solving. In fact, I often post my own discoveries http://www.scienceforums.net/topic/61237-discoveries-by-daedalus/ and create math challenges that I post in the Brain Teasers and Puzzles forum for others to solve: http://www.scienceforums.net/topic/60158-daedalus-first-challenge/ http://www.scienceforums.net/topic/60202-daedalus-second-challenge/ http://www.scienceforums.net/topic/60236-daedalus-third-challenge/ http://www.scienceforums.net/topic/61209-daedalus-fourth-challenge/ http://www.scienceforums.net/topic/67268-daedalus-fifth-challenge/ http://www.scienceforums.net/topic/77503-daedalus-sixth-challenge/ http://www.scienceforums.net/topic/77776-daedalus-seventh-challenge/ http://www.scienceforums.net/topic/78797-daedalus-eighth-challenge/ http://www.scienceforums.net/topic/79134-daedalus-ninth-challenge/ http://www.scienceforums.net/topic/80134-daedalus-tenth-challenge/ http://www.scienceforums.net/topic/87801-daedalus-eleventh-challenge/ http://www.scienceforums.net/topic/93095-daedalus-twelfth-challenge/ http://www.scienceforums.net/topic/95080-daedalus-thirteenth-challenge/ ScienceForums.net allows us to write mathematics in our posts using LaTeX, which contains syntax that can display just about any mathematical symbol or operator. Basically, there are tags that you use in your post that tells the forum software that you are using LaTeX. As seen in the following image, if you hover the mouse over any of the formulas you see here and left click on the equations, you should get a dialog that shows you the tags and the LaTeX used to produce the mathematical output: That was the intent of my post. Martin or Nota wanted to know what got us mathematicians hooked on math or, at least, tell others why we like it as to inspire them or give them hope. It seems like this person has a grudge because they wanted to be able to understand math but couldn't because their teachers didn't make it exciting or only had them learn equations and formulas without being able to explain how to use them to solve any problem they would like to know the answer. So, my reply was based on my experiences and I wanted to make it clear that my success with understanding math is due to my own curiosity and love for the subject. If you are truly interested in something, you cannot rely on someone else to teach you everything about it. Sure, teachers are there to teach us various topics that we are required to learn or want to learn so that we can function in society and figure out what we want to do with our lives, but it's ultimately up to us to determine how far we want to take our education. If you really like something, then you will ask questions and find someone who can answer them. I find that we are all in some way experts at things we love to do because we will invest time and effort in learning these things. If something is boring to you, then you are not going to invest the time and effort it takes to master the subject. For instance, I love playing guitar, piano, and writing musical compositions. So, I like to use the rock star analogy because a lot of people would love to be a rock star or famous musician because the idea of having talent, fame, money, and getting the girls or guys is intriguing to them. However, learning to play a musical instrument can be very boring in the beginning because you are learning things like scales, chords, and music theory, which may not pertain to the actual reasons of why you want to be a musician in the first place. Plus, it's really hard to make your fingers hit all of those notes correctly. So, it's extremely frustrating when you start out because you want to be able to play guitar like Eddie Van Halen so you can impress all those girls at school, but you find that you are struggling trying to play "Mary Had a Little Lamb". You really have to put in a lot of time and effort practicing these things and learning all of those boring concepts if you want to be able to play music and even more so if you want to be a rock star. So, when it comes to why I love math, I gave examples based on the binomial expansion theorem because most people that have taken high school level math should be familiar with that theorem and it still amazes me to this day how often it comes up in problems that I have solved and are currently working on solving such as the Collatz conjecture. I don't expect most people to understand the examples I gave because they are complex. However, I do hope that people who want to learn mathematics and be able to reach a level of understanding that allows them to tackle these type of complex mathematical problems will see that it takes more then just relying on someone else to explain it to them to get there. You have to have a curiosity and love for the subject that enables you to push through all the boring stuff and pursue a mastery of the subject yourself. This applies to everything you want to do in life. If you are truly interested in something, then you will ask the questions and pursue the answers yourself. If your current teachers can't help you, then your motivation and curiosity will force you to find someone who can. Most of my teachers in high school could not answer a lot of the questions I had about the mathematics pertaining to problems that I was solving for myself. However, I didn't let that stop me from finding the answers. Either my teachers would point me in the right direction, or they referred me to someone who could help. All it took from me was the time and effort to pursue the subject.

Having an insatiable interest in science is why you should've cared, but that's not why you failed. Simply put, mathematics is boring to you and you didn't even bother investigating the subject on your own. It's unfortunate that your math teachers didn't know how to inspire you but it's not their fault that you didn't have an interest in understanding mathematics. I actually liked working the equations and solving the problems even though I had a tough time at first memorizing the formulas, but I also understood that math is used to solve problems beyond just learning the equations and processes. As such, I was constantly seeing patterns in numbers and questioning my math teachers about equations that I would solve that predicted cool little patterns that I found. For instance, in the tenth grade, I learned how to expand binomials, [math](a+b)^n[/math], the hard way by multiplying [math](a+b)[/math] by itself [math]n[/math] times. The first night we had homework, I figured out the binomial expansion theorem myself by developing a process that predicted the coefficients and powers of the expanded binomial. I didn't even know there was a binomial expansion theorem because we hadn't learned it yet, but I showed it to my math teacher the next day. I thought it was cool because it allowed me to do my homework using one line instead of half a sheet of paper, and coach Ware agreed. So, he let me teach it to the class and everyone got to use it until we learned the actual binomial expansion theorem. Now, you might say that I had a good math teacher, but coach Ware was just teaching us math as is normally taught. After all, he was the school's basketball coach and not a mathematician. If I didn't have an interest in mathematics, I would've never got to teach the class that day and explain how I figured out how to expand binomials. As Bignose has stated, teachers should focus on problem solving skills. This is what mathematics is all about; being able to solve problems. Martin or Nota, I understand that you feel kind of cheated because instead of learning how to use mathematics to solve problems you learned equations and formulas, which are the tools we use to solve such problems. You were given an equation and asked to plug in numbers to get a result, but you were never given a set of numbers and asked to produce the equation. You see, the first step in mastering problem solving is being able to derive an equation that produces an observed pattern of numbers. However, you can only do this if you know all those little equations and rules like factoring that allow you to develop such equations. The problem you had is that you wanted to be a rock star but you didn't want to put in all that boring, hard work of learning how to play and write the music. Do you see what I'm saying? The binomial expansion theorem is just another equation that allows us to generate Pascal's triangle and calculate coefficients that occur when we expand binomials. Pretty boring stuff huh? However, did you know that the binomial expansion theorem can be found in just about every single problem in number theory? It still blows my mind to this day. When I was learning trigonometry, I learned that there are polynomials that predicts the summation of [math]x^p[/math]. 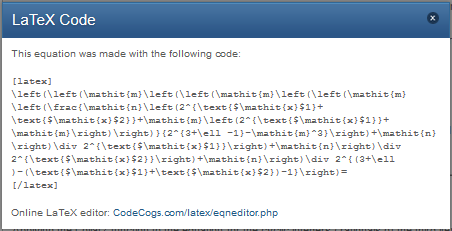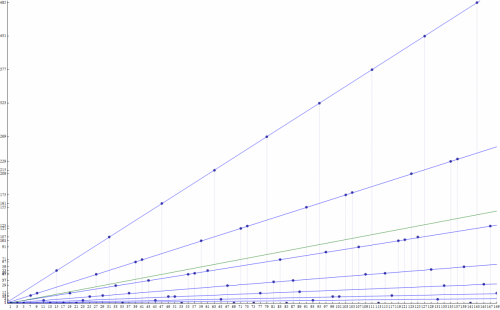However, my teacher only knew the polynomial for the summation of [math]x^1[/math], which is [math]\sum_0^n x=\frac{n(n+1)}{2}[/math] It took me one year and three months, but I solved the equation that predicts the sum of [math]x^p[/math], which allowed me to derive and extend Newton's interpolation formula: As you can see in the above quote, the binomial expansion theorem occurs when taking the deltas or products of the set of numbers when interpolating an equation for them. If I didn't know all of those boring formulas, I would never be able to solve such exciting problems. My latest work on the Collatz conjecture, an unsolved problem in mathematics, actually has the binomial expansion theorem embedded in it where the diagonal numbers in Pascal's triangle determines the number of lines that pass through points that occur for each iteration of the Collatz function. 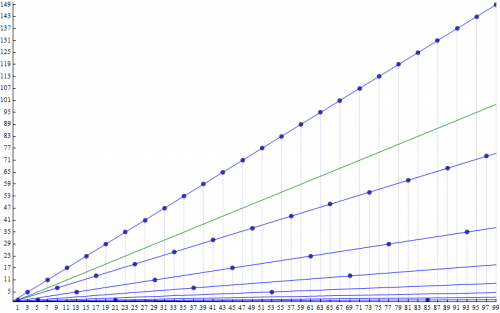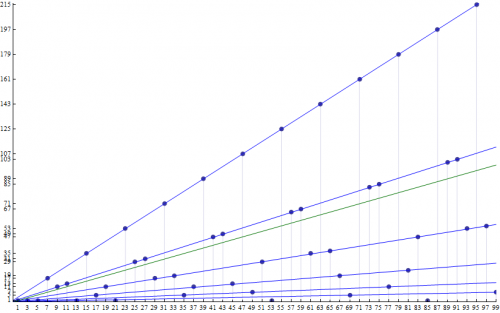For instance, the following graph shows the lines that goes through the points for one iteration of the Collatz function: Here is the graph for two iterations of the Collatz function: Here is the graph for three iterations of the Collatz function: You'll notice that for the first iteration, the points are equally distributed along each line. However, you'll see that the points occur in repeating clusters for the second and third iterations along each line. The pattern for the second iteration is that the top line has its points equally spaced but there are 2 points clustered along the second line. 3 points clustered along the third line and so forth. The pattern again changes for the third iteration. The top line has its points equally spaced with 3 points clustered along the second line. 6 points clustered along the third line and 10 points clustered along the fourth line and so forth. The green line is the function, [math]f(x)=x[/math] and is used to determine where iterations of the Collatz function can cycle, which occurs where the blue lines intersect the green line. Some really cool, mind-blowing facts from applying my problem solving skills to the Collatz conjecture. First, by analyzing where the blue lines intersect the green line, we can conjecture that cycles can only occur when the points are near zero. The slopes of the blue lines decrease exponentially and therefore diverges from [math]y=x[/math] as [math]x[/math] approaches infinity. This means that there are no hidden cycles greater than 1 for extremely large values of [math]x[/math]. It doesn't completely rule out the possibility of a large value of [math]x[/math] from being a cycle because each point in a cluster defines a line that is parallel to other points in the cluster, and these parallel lines eventually no longer appear to occur on a common line as the number of iterations approach infinity. However, because I have the equation that predicts all possible lines for all point clusters for any iteration of the Collatz function, I have derived the equation that predicts all possible points that cycle by setting the equations that determines the blue lines equal to the equation for the green line and solving for [math]x[/math]. For my own purposes, I will withhold this formula, but I don't mind showing you the expanded form of the equation for the first few iterations (if you want to beat me to the proof, you'll need to do the work ): The intersection points for the first iteration where [math]m=3[/math] and [math]n=1[/math] as defined by the "normal" Collatz function where [math]\ell[/math] is the index of the line cluster and the number of iterations are expressed as constants (I extended it to work with any set of odd numbers [math]m[/math] and [math]n[/math]): [math]\left(\frac{\mathit{n}}{2^{1+\ell -1}-\mathit{m}^1}\right)[/math] The intersection points for the second iteration: [math]\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)}{2^{2+\ell -1}-\mathit{m}^2}\right)[/math] The intersection points for the third iteration: [math]\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}+\text{$\mathit{x}$2}}+\mathit{m}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)\right)}{2^{3+\ell -1}-\mathit{m}^3}\right)[/math] The intersection points for the fourth iteration: [math]\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}+\text{$\mathit{x}$2}+\text{$\mathit{x}$3}}+\mathit{m}\left(2^{\text{$\mathit{x}$1}+\text{$\mathit{x}$2}}+\mathit{m}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)\right)\right)}{2^{4+\ell -1}-\mathit{m}^4}\right)[/math] You'll notice that the above equations have [math]x_1,x_2,x_3[/math] etc.. These variables define the number of twos that actually divide the even numbers that occur when iterating an odd number. However, it doesn't include the number of twos for the last odd number that occurs during a given iteration. If you were to apply the Collatz function to the odd numbers or rational numbers that have odd numerators defined by the above equations, you will find that they do indeed cycle in the specified number of iterations: Applying the Collatz function to the equation for the cyclic integers / rationals of the first iteration: [math]\left(\left(\mathit{m}\left(\frac{\mathit{n}}{2^{1+\ell -1}-\mathit{m}^1}\right)+\mathit{n}\right)\div 2^{(1+\ell )-1}\right)=\left(\frac{\mathit{n}}{2^{1+\ell -1}-\mathit{m}^1}\right)[/math] Applying the Collatz function to the equation for the cyclic integers / rationals of the second iteration: [math]\left(\left(\mathit{m}\left(\left(\mathit{m}\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)}{2^{2+\ell -1}-\mathit{m}^2}\right)+\mathit{n}\right)\div 2^{\text{$\mathit{x}$1}}\right)+\mathit{n}\right)\div 2^{(2+\ell )-(\text{$\mathit{x}$1})-1}\right)=\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)}{2^{2+\ell -1}-\mathit{m}^2}\right)[/math] Applying the Collatz function to the equation for the cyclic integers / rationals of the third iteration: [math]\left(\left(\mathit{m}\left(\left(\mathit{m}\left(\left(\mathit{m}\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}+\text{$\mathit{x}$2}}+\mathit{m}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)\right)}{2^{3+\ell -1}-\mathit{m}^3}\right)+\mathit{n}\right)\div 2^{\text{$\mathit{x}$1}}\right)+\mathit{n}\right)\div 2^{\text{$\mathit{x}$2}}\right)+\mathit{n}\right)\div 2^{(3+\ell )-(\text{$\mathit{x}$1}+\text{$\mathit{x}$2})-1}\right)=[/math] [math]\left(\frac{\mathit{n}\left(2^{\text{$\mathit{x}$1}+\text{$\mathit{x}$2}}+\mathit{m}\left(2^{\text{$\mathit{x}$1}}+\mathit{m}\right)\right)}{2^{3+\ell -1}-\mathit{m}^3}\right)[/math] As we can tell by applying the Collatz function to the intersection points, the number of twos that divide the last odd integer / odd rational number is equal to [math](r+\ell)-(x_1+x_2+\cdots)-1[/math]. If [math]x_1,x_2,\cdots[/math] are greater than 0, and [math]r+\ell-1 > x_1+x_2+\cdots[/math], then the numbers defined by the equations for the intersection points do indeed cycle in [math]r[/math] iterations of the Collatz function and define odd integers or rational number where the numerator is odd. The next step is to show that 1 is the only integer greater than 0 that cycles and all other positive numbers are rational. These intersection points combined with other equations that I have derived that maps out the odd integers that occur while iterating the Collatz functions indefinitely for an initial odd number can be used to construct a proof of the Collatz conjecture and solve an 80 year old, unsolved math problem. So, you can see how important it is to know all of these boring equations and formulas because they allow us to delve into the unknown and solve problems that have remained unsolved for decades and even centuries! Although your teachers could never teach you how to solve the Collatz conjecture, they did try to teach you the tools that you could've used to do it. Ultimately, it was up to you to take the leap into the world of mathematics, but it was boring to you, which is perfectly ok. Not everyone was meant to play with numbers Just remember, if you want to be a rock star, you have to practice playing and writing music. Even if the work to get there is boring, the reward is definitely worth the effort \,,/

This is really easy using Newton's interpolation method. I extended Newton's method to allow for increasing summations of [math]f(x)[/math] and to exponential equations too, which I demonstrated in my Fourth Challenge and allows us to derive an exponential equation that will also interpolate [math]f(x)[/math] as well as increasing products of [math]f(x)[/math]. Note: the exponential interpolation method cannot handle zeroes in the range. The polynomial the interpolates [math]f(x)[/math] is [math]\frac{359}{6652800}x^{11}-\frac{977}{259200}x^{10}+\frac{42001}{362880}x^{9}-\frac{17761}{8640}x^{8}+\frac{14137327}{604800}x^{7}-\frac{15371867}{86400}x^{6}+[/math] [math]\frac{111321821}{120960}x^{5}-\frac{2605751}{810}x^{4}+\frac{3355619803}{453600}x^{3}-\frac{2379611}{225}x^{2}+\frac{58055651}{6930}x-2743[/math] I attached a Mathematica 7 file that shows how I derived the above polynomial and proves that it interpolates the specified range. Polynomial.zip

Again, repeating something doesn't somehow manifests itself into a theory of how time dilation is busted. It doesn't matter if you want me to imagine a rocket at the coordinates (0,0,0) and move it to (0,1,0) without requiring the passage of time or leaving an immediate past as you like to call it. None of that nonsense supports your claims that time dilation is busted. The sad thing is that you didn't even try to understand the post where I explained relativity to you because you are firm in the understanding that you must be right and everyone else is wrong. Quite frankly, I could care less if you wish to remain ignorant, at least I tried. There is no amount of nonsense that you can spout to change anyone's mind. To do that, you need to define your ideas with the same rigor that is expected of everyone else.

Do you realize how nonsensical that statement is?

Well, it's better to be a Rick than a Morty

Unfortunately, you haven't made a single statement that shows time dilation is not true. You can continue to ignore everyone here and all of the experimental evidence all you like. Your idea isn't even expressed in the form of a valid scientific theory. So, you've got a tremendous amount of work you need to do and experiments to conduct if you want to dethrone relativity. Of course, considering that cookies can't think, you definitely are the smartest one in the jar ; )