Daedalus

As I stated in a thread started by Morgsboi that was moved to the speculations forum: This is why division by zero is undefined: Given that [math]z=\frac{y}{x}[/math] assigns to each point ([math]x[/math], [math]y[/math]) a real number [math]z[/math]. Then the limit[math], \ \lim_{(x, y) \to (a, b)} \frac{y}{x} \ ,[/math] can only exist if all paths in the domain, [math]\{(x,\, y) \in \mathbb{R}^2\}[/math], approach the same value. If we choose multiple lines (paths in the domain) of the form [math]y=m\, x[/math], then as [math]x[/math] approaches zero [math]y[/math] also approaches zero such that: [math]\lim_{(x, y) \to (0, 0)} \frac{y}{x} \ =\ \lim_{x \to 0} \frac{m\, x}{x} = m[/math] Notice how the value of the limit depends on the direction at which you approach zero - different values of [math]m[/math]. Since we get different values for the limit as [math]x[/math] and [math]y[/math] approach zero, the limit does not exist. Hence the reason why division by zero is undefined.

That's perfectly fine. If you are really interested in mathematics, then I would suggest that you ask your math teachers as many questions as possible. In addition, it wouldn't hurt to try and get into some AP (advanced placement) math classes if your school has them. That way you can earn college credit if you score high on the AP test. As you progress in your studies of mathematics, you will begin to understand the type of math, multivariate calculus, that I used to demonstrate why division by zero is undefined.

This is why division by zero is undefined: Given that [math]z=\frac{y}{x}[/math] assigns to each point ([math]x[/math], [math]y[/math]) a real number [math]z[/math]. Then the limit[math], \ \lim_{(x, y) \to (a, b)} \frac{y}{x} \ ,[/math] can only exist if all paths in the domain, [math]\{(x,\, y) \in \mathbb{R}^2\}[/math], approach the same value. If we choose multiple lines (paths in the domain) of the form [math]y=m\, x[/math], then as [math]x[/math] approaches zero [math]y[/math] also approaches zero such that: [math]\lim_{(x, y) \to (0, 0)} \frac{y}{x} \ =\ \lim_{x \to 0} \frac{m\, x}{x} = m[/math] Notice how the value of the limit depends on the direction at which you approach zero - different values of [math]m[/math]. Since we get different values for the limit as [math]x[/math] and [math]y[/math] approach zero, the limit does not exist. Hence the reason why division by zero is undefined.

Well the point is that it does not equal anything because the limit equals zero.

Well... considering the following: [math]\lim_{x \to 0} \frac{0}{x} = 0[/math], Suggests that 0/0 does not represent a universe where everything came from nothing.

You can always use the Riemann sum to approximate [math]\pi[/math]. Although, it may not be the most efficient method: [math]R_n=\sum_{k=0}^{n-1} f(x_k) \, \Delta x \approx \pi[/math] [math]4 \times R_1 \ = 4.000000000[/math] [math]4 \times R_2 \ = 3.732050808[/math] [math]4 \times R_3 \ = 3.584220045[/math] [math]4 \times R_4 \ = 3.495709068[/math] [math]4 \times R_5 \ = 3.437048829[/math] [math]4 \times R_6 \ = 3.395316356[/math] [math]4 \times R_7 \ = 3.364086195[/math] [math]4 \times R_8 \ = 3.339818144[/math] [math]4 \times R_9 \ = 3.320407605[/math] [math]4 \times R_{10} = 3.304518326[/math] [math]...[/math] [math]4 \times R_{1000} = 3.143555467[/math] You might be interested in these methods: http://en.wikipedia....tions_of_%CF%80

This sounds more like a math question than it does an engineering question. In this case, I would simplify the rules because it really doesn't matter which set we choose to increment. Basically, you are solving for the maximum number of rounds you can go before a set terminates (a member of the set equals the value of T). It would be easier to take the largest member in each set: [math]S_1=\{a_i\}_{i=1}^{n}, \ \ M_1=\text{max} \ S_1[/math] [math]S_2=\{b_i\}_{i=1}^{n}, \ \ M_2=\text{max} \ S_2[/math] [math]S_3=\{c_i\}_{i=1}^{n}, \ \ M_3=\text{max} \ S_3[/math] etc... Calculate the number of rounds [math]R_1, \ R_2, \ R_3, \ \text{...}\, , \ [/math] each set can make before terminating: [math]R_1 = T - M_1 - 1[/math] [math]R_2 = T - M_2 - 1[/math] [math]R_3 = T - M_3 - 1[/math] etc... Add up the number of rounds for each set to get the total number of rounds: [math]R_{\, \text{total}} = \sum_{k=1}^{m} R_k[/math] If you want to include the round that terminates the process, just add one: [math]R_{\, \text{total}} = 1 + \sum_{k=1}^{m} R_k[/math] Now for the next part of the problem: It sounds like the process waits for time [math]t[/math] to elapse after making a choice each round (increment one set and decrement the others). In that case, the process would not terminate because we can decrement the set we incremented the previous round, and increment the set we just decremented. [math]R_0: \ A=\{6,4,3,3\}, \ B=\{5,4,3,3\}[/math] [math]R_1: \ A=\{5,3,2,2\}, \ B=\{6,5,4,4\}[/math] [math]R_2: \ A=\{6,4,3,3\}, \ B=\{5,4,3,3\}[/math] etc..

I wouldn't call this a detailed analysis of 1/4 of a circle using rectangles when the underlying principle is based on the Riemann sum with only ten partitions. [math]f(x)=\sqrt{1-x^2}, \ \ \ \ \Delta x = \frac{b-a}{n}, \ \ \ \ x_k = a + k \ \Delta x[/math] The area of the region [math]R[/math] can be approximated using [math]n[/math] rectangles such that: [math]R_n = \sum_{k=0}^{n-1} f(x_k) \ \Delta x \ \ \ \ \text{or} \ \ \ \ R_n = \Delta x \ \sum_{k=0}^{n-1} f(x_k)[/math] Since integrating [math]f(x)=\sqrt{1-x^2}[/math] on the interval [math][0, 1][/math] is 1/4 the area of a circle with radius one, multiplying the above Riemann sum by 4 will approach the value [math]\pi[/math] as [math]n[/math] aproaches [math]\infty[/math]: [math] 4 \times \lim_{n \to \infty} R_n \ = \ 4 \times \lim_{n \to \infty} \ \sum_{k=0}^{n-1} f(x_k) \ \Delta x \ = \ 4 \times \int_0^1 f(x) \ dx \ = \ 4 \times \frac{\pi}{4} \ = \ \pi[/math] You can use the mid-point rule, the trapezoidal rule, or Simpson's rule to get better approximations when dealing with a finite number of rectangles.

Sorry about that. I based my reply on the assumption that he knew parts a - c. I'll trim it back next time : )

The above assumption is incorrect. The largest / smallest possible number for any electronic calculating device is not [math]\pm 9999999999[/math]. It is actually based on the the precision of the FPU as described here: Double-precision floating-point format Furthermore, you have neglected to consider calculators that are based on arbitrary precision arithmetic. You have erroneously related the base of the number system to the number of digits for your largest / smallest number. My TI-89 can handle base 10 numbers above and below your specified range. Here you are trying to apply the squeeze theorem. However, there is a huge problem with your method. You do not apply the limit correctly. Let me demonstrate the issue. You are claiming that if: [math]z = \frac{x}{y}[/math] then [math]z = \frac{x}{2}\left(\frac{1}{y'}+\frac{1}{y''}\right)[/math] where [math]y' = \lim_{n \to 0^-} (y-n)[/math] and [math]y'' = \lim_{n \to 0^+} (y+n)[/math] such that [math]\frac{x}{y'} > \frac{x}{y} > \frac{x}{y''}[/math]. However, as stated in your method, you are not taking the limit as [math]n[/math] approaches zero. Instead, you are claiming that calculating devices cannot cover the entire set of reals, which makes it possible to choose some value [math]\epsilon > 0[/math] such that: [math]z = \frac{x}{2}\left(\frac{1}{y'}+\frac{1}{y''}\right)=\frac{x}{y}[/math] The above statement is wrong because we are dealing with the set of real numbers!!! What you are actually doing is as follows: [math]z = \lim_{n \to \epsilon} \frac{x}{2}\left(\frac{1}{y-n}+\frac{1}{y+n}\right)=\frac{x\, y}{y^2-\epsilon^2} \ne \frac{x}{y}[/math] Example 1 - you claim that: The problem with the above example is that: [math]\left(\frac{1}{5-0.000000001}+\frac{1}{5+0.000000001}\right) \ne \frac{2}{5}[/math] Your method only approximates the result of the division: [math]\left(\frac{1}{5-0.000000001}+\frac{1}{5+0.000000001}\right) \approx \frac{2}{5}[/math] You cannot claim that this allows you to divide by zero over the set of reals. It is a logical fallacy: [math]\left(\frac{1}{0-0.000000001}+\frac{1}{0+0.000000001}\right) \ne \frac{2}{0}[/math] Now I will address your latest post: Your method is based on limits, which forces us to evaluate it with the tools of calculus. The above statement is pure speculation because you are trying to relate your method to a physical application of dividing by zero. We are not talking about physical processes (although it would not matter if we were because the mathematics of indeterminate forms - [math]1/0, 0/0[/math], etc... - can have limits that are zero, infinity, etc...). We are discussing the result of a division by zero as defined by your method: This is where you reveal that you are not truly dividing by zero. Defining a subset of real numbers does not allow for division by zero: The problem with this statement is that it does not matter which set you choose, A or B. We are not studying the properties of set B. We are analyzing the operations that you are applying to the set. Once you realize this, you will see that your method is not dividing by zero: [math]\frac{x \times 0}{0-\epsilon^2} \ne \frac{x}{0}[/math] It does not matter if we write your method as an equation of two variables or three. The results are the same: [math]\frac{x \, y}{(y-0.000000001)(y+0.000000001)} \ne \frac{x}{y}[/math] or [math]\frac{x \, y}{(y-\epsilon)(y+\epsilon)} = \frac{x \, y}{y^2-\epsilon^2} \ne \frac{x}{y}[/math] The only reason why your method produces a zero when [math]y = 0[/math] is because: [math]\frac{x \times 0}{0 - \epsilon^2} = \frac{0}{-\epsilon^2} = 0[/math] The key point that I will make here is that you are calculating up to a limited number of digits. This means that your method has two discontinuities where [math]y^2 = \epsilon^2[/math]. However, because you state that you are only considering set B, your method cannot approximate values of [math]|y| > L[/math] because you incorrectly suggest that a base 10 calculating device cannot handle numbers larger or smaller than [math]\pm L[/math]. There is one more thing I would like to add in response to your claims: 1.) Your method is not based on the rules of mathematics for division. It is based on the function [math]\text{B}(x,y)=\frac{x\, y}{y^2-\epsilon^2}[/math] that you have defined where [math]x[/math] and [math]y[/math] are variables, and [math]\epsilon[/math] is a constant such that [math]\epsilon > 0[/math]. 2.) Stating that your method is simple and easy to use is an opinion and not a fact. 3.) Your method when [math]y=0[/math] is equivalent to [math]\frac{x \times 0}{0-\epsilon^2} = -\frac{0}{\epsilon^2} \ne \frac{x}{0}[/math] and does not divide by zero. However, [math]f(x, 0)=0, \ \ \{x \in \mathbb{R} \ | \ -\infty < x < \infty\}[/math]. 4.) Your method produces incorrect values for the ratios tan 90, csc 0, sec 90, and cot 0. As for claim 5, you are more than welcome to modify your calculating devices to use your method instead of actually doing division. Just leave my devices alone : ) In closing, you should consider the following: [math]\lim_{y \to 0} \frac{0}{y} = 0[/math] which is similar to: [math]\lim_{y \to 0} \frac{x \, y}{y^2 - \epsilon^2} = 0[/math] However, these limits are not equal: [math]\lim_{y \to 0^-} \frac{1}{y} = -\infty \ \ \ \ \lim_{y \to 0^+} \frac{1}{y} = \infty[/math] This is why we call these things indeterminate forms.

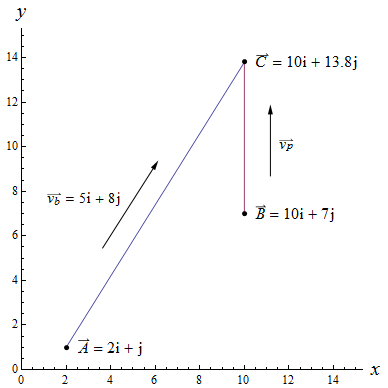
The following graph allows us to visualize the problem: [math]\vec A[/math] is the position vector for where the ball was kicked, [math]\vec v_b[/math] is the velocity vector of the ball, [math]\vec B[/math] is the position vector where the player starts running north, [math]\vec v_p[/math] is that player's velocity vector, and [math]\vec C[/math] is the position vector where the player intercepts the ball. You already know parts a - c: a.) The speed of the ball is equal to the magnitude of [math]\vec v_b[/math] such that: [math]|\vec v_b|=\sqrt{5^2+8^2}=\sqrt{89}\, m/s[/math]. b.) The position vector of the ball after [math]t[/math] seconds is: [math]r_b(t)=\vec A + t \, \vec v_b=(2+5t)i+(1+8t)j[/math]. c.) The time when the ball is due north from [math]\vec B[/math] is when the [math]i[/math] component of the ball's position vector equals the [math]i[/math] component of [math]\vec B[/math]: [math]2+5t = 10\, m, \ \ t=8/5 \, s = 1.6\, s[/math] Now for part d: 1.) You already know it takes [math]1.6\, s[/math] for the ball to be located due north of [math]\vec B[/math]. 2.) You also know the position that the player at [math]\vec B[/math] begins running for the ball. 3.) You also know that the player runs due north such that the position vector of the player after [math]t[/math] seconds is: [math]r_p(t)=\vec B + t \, \vec v_p=10i+(7+v\, t)j[/math] Now all you need to do is set the position vector of the ball [math]r_b(t)[/math] equal to the position vector of the player [math]r_p(t)[/math] at time [math]1.6\, s[/math] and solve for [math]v[/math]: [math](2+5(1.6))i+(1+8(1.6))j = 10i+(7+v(1.6))[/math] [math](2+5(1.6))i = 10i[/math] [math](1+8(1.6))j = 13.8j = (7+v(1.6))j[/math] The rest is up to you : )

doG, I wouldn't pay much attention to what he is selling. I have already shown that he is confused about dealing with indeterminate forms. He is comparing a function of three variables with a function of two, and trying to say that both are equal to each other.

Just because you are taking a limit does not mean that you are dividing by zero. You are applying Calculus to analyze the following equation: [math]\frac{x \, y}{y^2 - z^2}[/math] which is not equal to: [math]\frac{x}{y}[/math] I would recommend that you learn some Calculus before making such assertions. You are incorrectly comparing two different indeterminate forms.

As Cap'n Refsmmat pointed out: This actually implies that the Bhartiya New Rule for Fraction is ill defined, and does not actually equal the result of the division. This mathematically flawed rule is based on the following limit: [math]\lim_{n \to 0}\frac{x}{2} \left(\frac{1}{y-n}+\frac{1}{y+n}\right)=\lim_{n \to 0}\frac{x}{2} \left(\frac{y+n}{(y-n)(y+n)}+\frac{y-n}{(y+n)(y-n)}\right)=\lim_{n \to 0}\frac{x}{2} \left(\frac{2y}{y^2-n^2}\right)=\frac{2 \, x \, y}{2 \, y^2}=\frac{x}{y}[/math] However, B.N.R.F. is based on the precision of a floating point processor (FPU). Therefore, [math]n[/math] does not approach 0, but some other value [math]\epsilon[/math]. This affects the result of the limit: [math]\lim_{n \to \epsilon}\frac{x \, y}{y^2-n^2}=\frac{x \, y}{y^2-\epsilon^2}=\frac{x}{y}\left(\frac{1}{1-\frac{\epsilon^2}{y^2}}\right) \ne \frac{x}{y}[/math] The reason why this method produces incorrect results when dealing with division by zero is as follows: [math]\lim_{y \to 0}\frac{x \, y}{y^2-\epsilon^2}=\frac{0}{0-\epsilon^2}=0, \ \left \{\epsilon \in \mathbb{R} \, | \, \epsilon \ne 0 \right \}[/math] Where the actual limits for [math]\frac{x}{y}[/math] as [math]y[/math] approaches zero are: [math]\lim_{y \to 0^-}\frac{x}{y}=-\infty[/math] and [math]\lim_{y \to 0^+}\frac{x}{y}=\infty[/math]

After reading your word salad sprinkled with terminology obtained from watching the Discovery Science channel and Back to the Future, I will have to refer you to rule 1 of the speculations forum: I have to agree with Ophiolite: Perhaps the Trash Can would be a better forum for this thread.

I am planning to do some tutorials on integration once this semester is over. I've already been working with Capn' on this, and you can see that the last posting in the tutorials section was contributed by me. I just haven't had time lately to finish my tutorial on Riemann sums. I plan to not only cover integration, but also give real world examples of how to apply the integral.

This may be of some interest to the discussion: Galaxy Rotation Curves from General Relativity with Renormalization Group Corrections

Damn those lying dutchmen... I guess it's up to me to make a video of my sons and I flying with wings made of wax.

Poor Icarus...

I definitely want wings like this:

Ok... I watched the video and others by the OP. Let's just say that I'm going to be nice and withhold my comments.

Besides, I have discoverd my own equations which can produce numbers larger than yours: http://www.sciencefo...es-by-daedalus/ Oh... you are also not allowed to steal my equations. However, feel free to use them. Just make sure you bring them back when you are done.

I could care less about your calculations. Prime numbers are amongst the biggest known numbers that have meaning behind them. They are also quite common in science and mathematics. We still have no clue what your number means, and I don't think most of us actually care. It's not like we would win a Fields Medal for knowing your method.