Daedalus

Not that I actually believe this theory to be correct, but what you have sounds a lot like Vernon Brown's photon theory.

Hi John. I haven't had much sleep lately. I just realized that the sequence of points wasn't properly structured in a way that makes sense. I've been working with lists in Mathematica and I sometimes mix things up. Basically, what I am asking for is an exponential function that produces the following: [math]F(1)=1[/math] [math]F(2)=2[/math] [math]F(3)=3[/math] [math]F(4)=4[/math] [math]F(5)=5[/math] The function must be in the form: [math]F(x)=a^{f(x)} \, b^{g(x)} \, c^{h(x)}[/math] etc... Where [math]a[/math], [math]b[/math], [math]c[/math], etc.. are constants and [math]f(x)[/math], [math]g(x)[/math], [math]h(x)[/math], etc.. are functions of [math]x[/math] such as [math]x^2+2\, x + 1[/math]. I designed the challenge to show how an exponential function can approximate a linear function within a closed interval such as [math]\{x : 1 \le x \le 5\}[/math] and to demonstrate how we can derive an exponential function for any sequence of numbers. I'll give you a hint in that the solution involves mathematics similiar to the answer I gave for the second part of Daedalus' Second Challenge. Except I am only looking for the exponential function which produces the above sequence and not the formula that I derived to solve it : ) However, I'll give a five star rating to anyone who can provide the formula along with the exponential function.

My senior year in high school, I discovered a way to manipulate exponential functions to produce any sequence of numbers I desired. The challenge I am setting forth asks for the exponential function that produces the sequence: Edit: {{1,1}, {2,2}, {3,3}, {4,4}, {5,5}} That is, when [math]x[/math] is equal to one, [math]y[/math] is equal to one and so forth up to {5, 5}. {1, 2, 3, 4, 5} Such that: [math]F(1)=1[/math] [math]F(2)=2[/math] [math]F(3)=3[/math] [math]F(4)=4[/math] [math]F(5)=5[/math] The answer I am looking for only uses exponential functions of the form [math]a^{f(x)} \, b^{g(x)} \, c^{h(x)} \text{etc...}[/math] You are only allowed to use elementary operators. No infinite series, trigonometry, or any mathematics higher than algebra. The result must be in the form as expressed above and contain only one term. I will post the answer along with the formula in a couple of weeks unless someone can solve this problem : )

A frame of reference refers to a coordinate system used by an observer to measure position, orientation, and other related properties. Jack is watching the train go by, so from his frame of reference the train is moving and the world is stationary. Jill is on the train, so from her frame of reference the train is stationary and the world is moving. Jack and Jill can choose any frame of reference, but they would typically choose one that would simplify their measurements or calculations. You can think about this much like astronomers did long ago when they tried to determine the motions of the planets. The path of the Mars from an Earth centered coordinate system is very complex with loops, where a sun centered coordinate system showed that Mars has a very simple elliptical path.

Hummingbird UAV:

Agreed. However, I based my response on the fact that you experience no force while travelling at a constant speed (ignoring gravity of course). That is why I made a statement about acceleration in that [math]F=m\, a[/math]. Even though the question was a hypothetical about if we somehow managed to move at the speed of light in our three dimensional space, one could argue that we are moving at the speed of light in four dimensions because the magnitude of the 4-velocity of a massive particle in the rest frame is equal to c. However, I did not answer whether we would be conscious of everything all at once. Just that we would still have consciousness.

You are welcome Appolinaria. I figured you were just refering to a simple 4D shape such as the tesseract to demonstrate your point. I think you will find that my theory does provide adequate answers to some of your questions. However, Pantheory has a really good theory too which may be able to explain things differently. Here is a link to his theory of Pan : ) He often posts in the forums and will be able to answer some of your questions as well.

I was browsing the forum when I noticed your thread. I can answer most of these within the confines of accepted science, but I will have to explain a few of your questions using my theory : ) a.) 1.) Relativity defines the fourth dimension as time. Other theories, such as string theory and M theory, add many more dimensions. 2.) Depth is just another dimension. Light only slows down when moving through matter - Slow Light 3.) Light would act just like it would in a 3D world. It would just have one less dimension to travel through b.) 1.) A tesseract is a four-dimensional cube. Yes you can apply 3D geometry to create the 4D hyper-geometery. In essence the Tesseract is to a cube as a cube is to a square. 2.) Normally time and length in four dimensions are interpreted much like in relativity where time dilates and lengths contract. This is due to Lorentz transformations. 3.) Parallel universes can be derived from M theory. My theory of Temporal Uniformity (read the entire thread) describes something similiar to what you have, except I use a 3-sphere instead of a tesseract. c.) I believe we would be conscious no matter what speed we travelled at. However, we would lose consciousness if we accelerated / decelerated to fast. Obtaining a speed to where you were not moving at all is relative to your frame of reference. If you believe you had obtained such state, I could always choose a coordinate system to where I was stationary and you were moving. So there is no prefered frame of reference or rest frame. d.) Physics currently states that there is no center to the expansion of the universe. Space appears to be expanding everywhere and not from a common center. However, I hypothesize in Temporal Uniformity that the universe is an expanding 3-sphere which is why we do not see this center. e.) This depends on the theory you choose to reference. M theory proposes that two branes came together and that collision provided the energy which created our universe. The Big Bang does not define how the universe began unless you consider the Big Bounce theory. My theory falls more in line with the Big Bounce.

IrishCommander, you may be interested in a thread of mine: Quantization of Length. Heresy or Merit?

I believe Pantheory and I have the best or simplest definition for what time actually is: Time is an interval of motion / change

Next week we will discuss the equation for the path of rotating body moving outward along the W axis and derive time dilation accordingly. As promised, I will also post the interpolation equation that allows us to specify locations with respect to intervals that can be sampled at any given time. This is different from Newton's interpolation formula which requires each location to be sampled within equal intervals of time. Newton's interpolation formula: [math]\sum_{i=0}^{n-1} \left [ \sum_{j=0}^{i} \left [ \left ( -1 \right )^{j} \binom{i}{i-j} S_j \right ] \times \binom{i-t-1}{i} \right ][/math] The variable [math]n[/math] is the number of measurements or specified locations, [math]S_j[/math] is the location specified by the [math]j[/math] index, the [math]i[/math] index works in conjunction with the [math]j[/math] index, and [math]t[/math] is time.

That is exactly the conclusion that I have derived using mathematics in my theory of temporal uniformity. We move through four dimensional space at the speed of light.

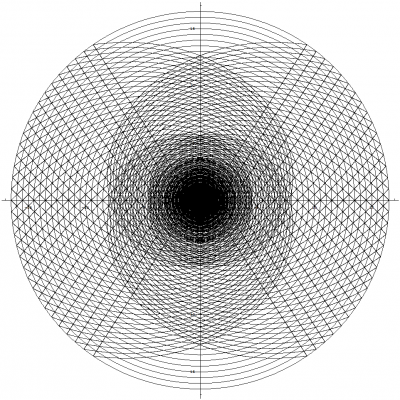
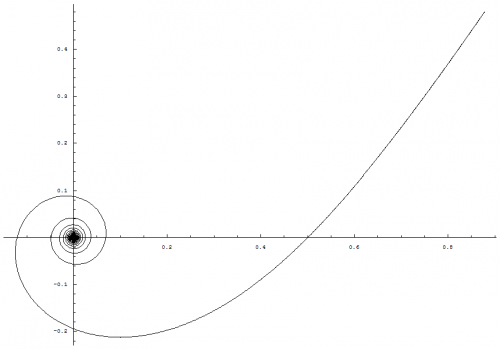
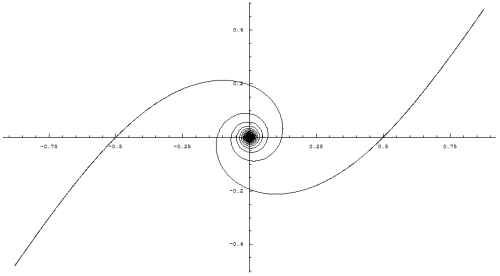
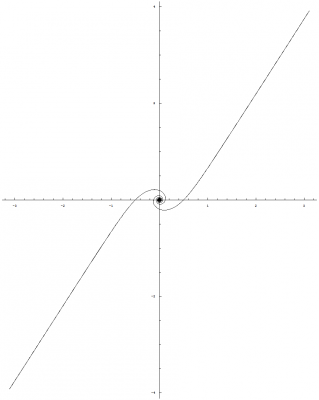
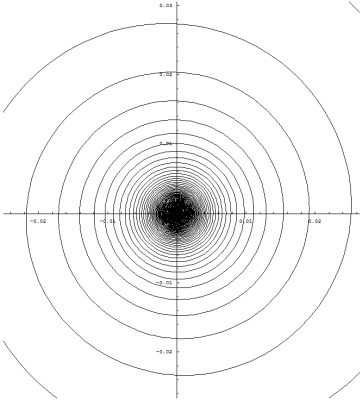
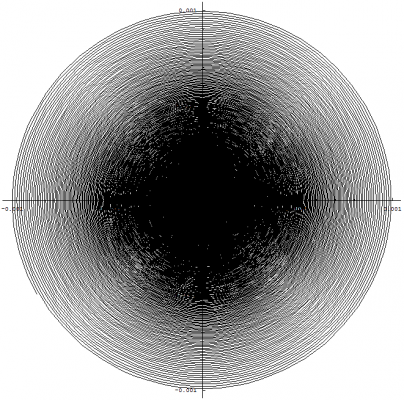
I know it has been a while since I last made a post, but I would like to continue and discuss the spiraling singularity and how I have interpreted this mathematical result of my equations. Before we get into the details, I would like to recap on what has brought us here and why I believe this mathematical framework gives us some insights into the nature of the universe. My original goal for Temporal Uniformity was to explain the phenomena of time by stating a hypothesis that dark matter is temporally displaced matter. This requires us to view the temporal dimension no differently than we do any other spatial dimension. This brings into question why we do not perceive this dimension to have any physical length, but experience a forward direction through time. This was derived by applying the mathematics of special relativity in such a way that when we solved for the speed along the W axis, we obtained the speed of light regardless of our motions through the other three observable spatial dimensions (I will re-derive the equation for the benefit of newcomers): The concept: Special relativity takes into account two main frames of reference. One is the rest frame where the observer is at rest and the other is a frame of reference in motion relative to the observer. Temporal uniformity takes into account an additional frame of reference called the Big Bang frame of reference. The Big Bang FoR has its origin located at the center of a four dimensional sphere that is expanding. This expanding sphere represents the Big Bang and we denote the subscript, [math]b[/math], to identify this FoR. The rest frame is called the time-normal FoR and is denoted with the subscript, [math]n[/math]. This leaves us with the FoR that is in motion relative to the time-normal FoR. We call this frame of reference the time-relative FoR and denote the subscript, [math]r[/math], to identify it. Both the time-normal and time-relative FoRs share the same magnitude of their space-time vectors from the Big Bang FoR's origin. In other words... from the Big Bang FoR we can say that the space-time vector with the tail located at the origin and the head located at the position of any observable body is equal in magnitude and therefore must be temporally aligned such that these bodies exist at the same point in time (i.e. everything you can see and touch exists at the same point in time). The time-normal FoR moves away from the Big Bang FoR's origin only along the W axis. But, the time-relative FoR not only moves away from the origin along the W axis, but also moves away from the time-normal FoR along dimensions perpendicular to the W axis. The key component to this view is that an observer located at the origin of the Big Bang FoR can rotate their FoR such that the time-relative FoR can become the time-normal FoR and vice-versa. This results in both, time-normal and time-relative, FoRs moving away from the Big Bang FoR's origin at the same rate as derived below: Time as defined by SR for an observer positioned at the origin of the Big Bang FoR: [math]\Delta t_{b} = \frac{2L}{c}[/math] where [math]L=|AB|[/math] Time as defined by SR for a body in the time-normal FoR being observed by an observer positioned at the origin of the Big Bang FoR (or vice-versa): [math]\Delta t_{n} = \frac{2\, N}{c}[/math] where [math]N=\sqrt{\left (\frac{V_{w} \times \Delta t_{n}}{2}\right )^{2}+L^{2}}[/math] [math]V_{w}[/math] is the velocity through the fourth dimension and [math]L=|AB|[/math] Multiply both sides by [math]c[/math] and square the results: [math]c^2 \, \Delta t_{n}^2 = 4 \, \left( \frac{V_{w}^2 \, \Delta t_{n}^2}{4} + L^2\right )=V_{w}^2 \, \Delta t_{n}^2 + 4\, L^2[/math] Subtract [math]V_{w}^2 \, \Delta t_{n}^2[/math] from both sides: [math]c^2 \, \Delta t_{n}^2 - V_{w}^2 \, \Delta t_{n}^2 = 4\, L^2[/math] Factor out [math]\Delta t_{n}^2[/math] from the left side: [math]\Delta t_{n}^2\, \left(c^2 - V_{w}^2\right ) = 4\, L^2[/math] Factor out [math]c^2[/math] from [math]c^2 - V_{w}^2[/math] on the left side: [math]\Delta t_{n}^2\, c^2\, \left(1 - \frac{V_{w}^2}{c^2}\right ) = 4\, L^2[/math] Divide both sides by [math]c^2\, \left(1 - V_{w}^2 / c^2\right )[/math]: [math]\Delta t_{n}^2 = \frac{4\, L^2}{c^2\, \left(1 -\frac{V_{w}^2}{c^2}\right )}[/math] Take the square root of both sides: [math]\Delta t_{n} = \frac{2\, L}{c\, \sqrt{1 - \frac{V_{w}^2}{c^2}}}[/math] Substitute [math]\Delta t_{b}[/math] in place of [math]2\, L / c[/math]: [math]\Delta t_{n} = \frac{\Delta t_{b}}{\sqrt{1 - \frac{V_{w}^2}{c^2}}}[/math] Time as defined by SR for a second body in the time-relative FoR being observed by an observer positioned at the origin of the Big Bang FoR without rotating the FoR (or vice-versa): [math]\Delta t_{r} = \frac{2\, R}{c}[/math] where [math]R=\sqrt{\left (\frac{V_{w} \times \Delta t_{r}}{2}\right )^{2}+\left (\frac{V_{r} \times \Delta t_{r}}{2}\right )^{2}+L^{2}}[/math] [math]V_{w}[/math] is the velocity through the fourth dimension, [math]V_{r}[/math] is the velocity relative to the first body in the time-normal FoR, and [math]L=|AB|[/math] Performing the same steps as we did above yields: [math]\Delta t_{r} = \frac{\Delta t_{b}}{\sqrt{1 - \frac{V_{w}^2}{c^2} - \frac{V_{r}^2}{c^2}}}[/math] Relating time dilation for both, time-normal and time-relative, FoRs through [math]\Delta t_{b}[/math]: [math]\Delta t_{b} = \Delta t_{n} \, \sqrt{1 - \frac{V_{w}^2}{c^2}}[/math] [math]\Delta t_{b} = \Delta t_{r} \, \sqrt{1 - \frac{V_{w}^2}{c^2} - \frac{V_{r}^2}{c^2}}[/math] This give us the following relationship: [math]\Delta t_{r} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}=\Delta t_{n} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}}[/math] We need to solve for [math]\Delta t_{r}[/math]. First we'll divide [math]\sqrt{1-V_{w}^{2}/c^2}[/math] by both sides: [math]\Delta t_{r} \frac{\sqrt{\left(1-\frac{V_{w}^{2}}{c^{2}}\right)-\frac{V_{r}^{2}}{c^{2}}}}{\sqrt{\left(1-\frac{V_{w}^{2}}{c^{2}}\right)}}=\Delta t_{n}[/math] Simplify the fraction by moving everything inside the square root and dividing out the terms in parentheses: [math]\Delta t_{r} \sqrt{1-\frac{\frac{V_{r}^{2}}{c^{2}}}{1-\frac{V_{w}^{2}}{c^{2}}}} = \Delta t_{r} \sqrt{1-\frac{\frac{V_{r}^{2}}{c^{2}}}{\frac{c^{2}-V_{w}^{2}}{c^{2}}}} = \Delta t_{r} \sqrt{1-\frac{V_{r}^{2}}{c^{2}-V_{w}^{2}}} = \Delta t_{n}[/math] Solve for [math]\Delta t_{r}[/math] by dividing the square root and its contents by both sides: [math]\Delta t_{r} = \frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}-V_{w}^{2}}}}[/math] Interpreting the result: This result makes sense because all observable bodies have a relative temporal velocity of zero, [math]V_{w}=0[/math], with all other observable bodies. In other words, we can see these objects and they do not disappear or appear at our point in time. This suggests that they are moving at the same rate through the temporal dimension as we are. This in turn yields the standard time dilation equation: [math]\Delta t_{r} = \frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}-0^{2}}}}=\frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}}}}[/math] However, we can determine our temporal velocity by solving for [math]V_{w}[/math]: [math]V_{w}=\frac{\sqrt{c^{2}(\Delta t_{n}^{2}-\Delta t_{r}^{2})+\Delta t_{r}^{2}\times V_{r}^{2}}}{\sqrt{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}=\sqrt{c^{2}+\frac{\Delta t_{r}^{2}\times V_{r}^{2}}{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}[/math] Since all observers will place themselves in the time-normal frame of reference, or the rest frame, they will have a zero relative velocity and their temporal velocity is equal to the speed of light, [math]V_{w}=c[/math]: [math]V_{w}=\sqrt{c^{2}+\frac{\Delta t_{r}^{2}\times 0^{2}}{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}=\sqrt{c^{2}}=c[/math] Because we move through the temporal dimension, W, at the speed of light, this fourth spatial dimension has collapsed according to length contraction. This is a valid statement if we consider the Big Bang FoR and vice-versa. This results with us perceiving three observable dimensions of space and one spatial dimension that becomes our temporal dimension, time: [math]L'=L\, \sqrt{1-\frac{V_{w}^{2}}{c^{2}}}=L\, \sqrt{1-\frac{c^{2}}{c^{2}}}=0[/math] This explains why we experience a forward motion through time but do not perceive a length along the temporal axis. I also explain this with a little more detail in the following section about the theory behind the math. The theory behind the math: The consequence of this result is that we are located on a layer of a four dimensional sphere, or 3-sphere, that is expanding at the speed of light: The mathematics in the previous posts demonstrate that as this sphere gets larger, the mathematics approach the equations found in special relativity due to the diminishing curvature of this expanding 3-sphere: [math]w'(u)^2+x'(u)^2+y'(u)^2=\Delta \tau^2 \left ( \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)+\frac{\mathit{Vl}_w^2}{c^2}\right )[/math] Taking the limit as [math]\mathit{Wl}_0[/math] approaches infinity: [math]\lim_{\mathit{Wl}_0 \to \infty} \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}=1[/math] [math]\lim_{\mathit{Wl}_0 \to \infty} \frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)=\left (\frac{\mathit{Vl}_x}{c}\right )^2[/math] [math]\lim_{\mathit{Wl}_0 \to \infty} \left (\frac{\mathit{Vl}_w}{c}\right )^2=\left (\frac{\mathit{Vl}_w}{c}\right )^2[/math] Time dilation - X and W axes: [math]\Delta \tau \left(\sqrt{ 1 - \left (\frac{\mathit{Vl}_x}{c}\right)^2-\left(\frac{\mathit{Vl}_w}{c}\right)^2}\right)^{-1}[/math] Note: Because we are talking about an expanding sphere, the W axis can be considered parallel to the local direction of the expansion when choosing a frame of reference which labels the temporal dimension as the W axis. We can hypothesize that dark matter fills the layers of this 3-sphere much like the layers of an onion, which would be nothing more than temporally displaced mass-energy. Because all mass-energy would be expanding with this 3-sphere, everything would be moving locally in the same direction and expanding outward at the speed of light. This means that the light from temporally displaced mass-energy will never be able to reach us and vice-versa. This explains why we don't see dark matter or any length along the W axis. This can be demonstrated if we visualize two photons travelling in the same direction, but offset from each other along the W axis. The photon at the end will not be able to catch up with the photon ahead of it. The photon at the front will not be able to change direction, and therefore will never share or intersect the same location with the photon behind it. However, this temporally displaced mass-energy would still be affected by gravitational fields from all spatial dimensions. This would explain why gravitational effects of dark matter can be seen as a halo around a galaxy and possibly explains why gravity seems to be weaker than the other forces of nature due to it propagating through all four dimensions of space. It would also explain why galaxies can rotate as fast as they do without flying apart as well as provide mass-energy located at our point in time with a scaffold to form around. If we look at any type of sphere, we can clearly form rays which propagate from the center of the sphere outward at any angle we wish to specify. Even though these rays would be moving away from the center of this sphere at an equal rate, they would have a different relative velocity from each other across the surface of this sphere in accordance to the angle they are propagating away from the center. This concept, along with considering localized effects of four-dimensional space, explains why the spaces between galaxies are expanding and why we do not see a center for this expansion. This brings us to an explanation for dark energy as discussed below. Massive bodies cannot go faster than the speed of light. Because the above mathematics shows us that everything is moving at the speed of light along the temporal axis, temporally displaced mass-energy cannot accelerate us toward the "future" because it would theoretically take an infinite amount of energy to do so. The inverse of this statement is that it would take an infinite amount of energy to decelerate a massive body that is moving at the speed of light. Therefore, temporally displaced mass-energy cannot pull us towards the "past". The only thing temporally displaced mass-energy could do is produce gravitational effects at our point in time and pull us along dimensions that are perpendicular to the temporal axis. Dark energy, which accelerates the expansion of space, can be visualized as temporally displaced mass-energy closer to the outer edge of this 3-sphere that is pulling us along with its expansion. Not only could there be more mass-energy closer to the edge of this expanding sphere, but it would also have had more time to expand resulting in much larger spaces between galaxies. This can be visualized by examining the cross section of the 3-sphere as shown in the above graphic. Not only can temporally displaced mass-energy explain dark matter, and possibly dark energy, but it can also explain dark flow if we consider that there is more mass-energy closer to the outer edge of this 3-sphere and that it has grouped into larger super clusters of galaxies than what we observe at our point along the temporal axis because it has had more time to do so: For the same reasons as above, we can also explain the Great Attractor: The reason why there would be a higher concentration of mass-energy toward the outer edge of this 3-sphere is due to the size of layers that radiated outward first. If we visualize a cross-section of a sphere that is composed of layers, we can see that the outer layers would have more mass-energy than the inner layers. Mass-energy in the outer layers would have been expanding longer than the inner layers. This implies that super clusters in the outer layers are composed of more galaxies than the inner layers resulting in a higher density for these outer layers. Also, the spaces between the galaxies in the outer layers would have had more time to expand and therefore would be larger than the spaces between the galaxies located in the inner layers. These spaces and super clusters can be seen as structures in the image of the WMAP for our point in time located along the W axis. I hypothesize that all layers along the W axis would have similiar composition: The mathematics I have derived in the previous posts can explain other cosmic phenomena such as the smoothness of the CMBR, or cosmic microwave background radiation. This has to do with the spiraling singularity as shown below: We normally think that everything expands away from each other much like what happens during an explosion. This causes a problem for what we see with the CMBR in how it can have such a uniform temperature. How is it possible for the entire CMBR to have this uniformly distributed temperature when one side of the expanding universe hasn't had enough time to communicate its temperature with the other side? However, the mathematics that I have derived tells a very different story: By analyzing a single photon path we can see that it actually forms a type of hyperbolic spiral. This means that the energy of the Big Bang did not just expand outward in all direction instantly, but converged to its present state as can be seen in the first image of the spiral that combines multiple photon paths. The above graph clearly shows that the photon path becomes incredibly dense towards time zero of the expansion of the 3-sphere, or Big Bang. We can also see the symmetry of two photon paths moving in opposite directions as shown below: By zooming out, we can see how these paths converge to straight lines as time approaches infinity: But we must zoom in on the spiral so that we can see how mass-energy could have communicated its temperature before expanding outward: Zooming in closer: The above image clearly illustrates how our mass-energy came into contact with mass-energy from the other side of the universe before expanding outward and converging to the expansion we see today, solving the horizon problem. The mathematics I have derived, along with the evidence provided by dark matter, dark energy, and dark flow, suggests that the idea of temporally displaced mass-energy is plausible. The big question now is what happens with inflation? Does this model allow for inflation or is it no longer valid within the context of temporal uniformity? I call on the experts to shed light on these questions to either validate or invalidate some of the speculative and hypothetical claims made within this post. That concludes tonight's posting. I hope you have enjoyed reading this and I look forward to any debate that may arise.

Oh no... the FErs are attacking!!!

A few posts back I provided a link to my theory of Temporal Uniformity. If the theory is correct, then time travel to the past or future is impossible. The effects of special relativity do not allow us to disappear from our present point in time and reappear in the past or future. Wormholes from general relativity, in theory, are suppose to be able to do this. Temporal Uniformity does not allow time travel to a memory of the past or to a memory that will exist in the future and resolves temporal paradoxes that these wormholes can create by treating time as a spatial dimension (i.e. we are currently located at a point along the temporal axis and continue to move forward from that point leaving the past behind. Therefore, a time traveller will encounter whatever mass-energy is currently located at whatever point they travel to along the temporal axis). This is how I explain dark matter and consequently dark energy, but that is getting off topic. You are more than welcome to read about it using the above link and we can discuss it on that thread. Also, there are many many threads here at SFN that discuss time and time travel. Feel free to search for those as well.

JustinW, you can edit your post and fix the quotation by pasting the text between the quote tags. I don't think that speed is truly behind the phenomena involved with relativity that affects time and space. Even though this is purely speculative, I would go as far as saying that it is energy density that drives time dilation and length contraction. The deeper the gravity well or the faster you go, the more energy is involved. Things tend to move faster through environments that have less energy. Superconductors are good examples of this in that electrons encounter very little to no resistance through the conductive material. Another way to look at this statement, is that it is easier to move through air than it is to move through water. Perhaps as you travel faster, energy density is what is slowing down clocks, atomic processes, aging, etc..., which affects our perception of reality. But, that is just a speculation.

Agreed. Which is why I pointed out the difference between relativity and clocks vs. the effect temperature has on a measuring rod. Relativity shows us that time dilation and length contraction is not based on flaws in the devices used to measure the phenomena, but an actuality of nature which affects our perception of reality.

Myuncle, it seems to me that you are getting wrapped up in the semantics of relativity. My idea on what time is may not be what is accepted by mainstream science. But... just because speed and gravity affects a clock's measurement of time, does not necessarily mean that "time", whatever it may actually be, is truly slowing down or speeding up. It simply states that our measurements of time are affected by these things due to the constancy of the speed of light, which in turn affects our physical nature and our perception of reality. Just because GPS satellites have a higher speed which affects their clock does not mean that the satellites are moving towards the future faster than we are and therefore measure a shorter time. It's not the same as a car that moves outside of your view because it is moving faster or slower and arrives at a destination sooner or later. In other words, the GPS satellites remain observable and do not disappear from our view leaving us behind while racing into the future. Even though relativity describes completely different phenomena, you can compare its effects similar to how temperature affects a measuring rod which will either contract or expand the rod. This changing of the rod's length due to temperature not only affects your measurements, but also affects any calculations of area, volume, speed, etc..., that you derive using those measurements. The greater the temperature differences between two identical rods, the greater the difference in measurements obtained by each rod. Your measurements and calculations are "relative" to your measuring rod. If we both have identical rods, I could use an equation that takes into consideration the temperature of both rods and derive the values you would measure by converting the measurements of my rod using the equation. The difference between relativity and this analogy is that, according to relativity, we would actually perceive a difference in time and space. In the above analogy, the difference in the measurements are due to temperature's effect on the rods and not that of perception. Just because we have invented clocks to measure time does not mean that the actual phenomenon of time is just an idea that we invented to facilitate our needs. My theory of Temporal Uniformity describes time as motion through a fourth spatial dimension. It doesn't mean that I am correct, but I try to back up my claims with either evidence or mathematical reasoning instead of just stating that time is as I say it is. The proof that you seek is as swansont has stated: However, as I have stated above, it is up to one's interpretation of perception to whether or not the phenomenon of time speeds up or slows down due to speed or gravity.

Wikipedia is always a good place to start. The following link will help refresh your memory as well as provide some other references for you to look at: http://en.wikipedia....iki/Precalculus I wish I could suggest a few books for you. I suppose you could go to Barnes & Noble, but I would imagine Amazon.com would have some good books as well as some electronic books you could buy. http://www.amazon.co...r/dp/0070572615 With Amazon you can at least check the ratings for the book and perhaps read a few reviews before buying : )

You are welcome : )

The rule is as follows: [math]\text{ln}(a \times b) = \text{ln}(a) + \text{ln}(b)[/math] We also know that: [math]\text{ln}(a^x)=x \, \text{ln} (a)[/math] and [math]\text{ln}(e)=1[/math] So we can conclude that: [math]\text{ln}(x \times e^{r\, t})=\text{ln}(x)+\text{ln}(e^{r\, t})=\text{ln}(x)+r\, t \, \text{ln}(e)=\text{ln}(x)+r\, t[/math]