Daedalus

Sorry uncool, [math]0^0[/math] is not defined and must be handled as an indeterminate form. This leads us to evaluate the limit of [math]0^x[/math] as [math]x[/math] approaches zero which would not produce the desired solution: [math]\lim_{x \, \to \, 0}0^x=0[/math] We could consider: [math]\lim_{x \, \to \, 0}x^0=1[/math] But, this would not produce the correct solution either. The solution itself does not rely on Calculus and, as stated, requires only elementary operators such as addition, subtraction, multiplication, division, and exponents that operate on the variable, [math]x[/math]. However, at risk of giving away the answer, you are on the right track by considering exponents : ) To up the ante, I will give the person who solves this five stars and reputation if they do so before I post the solution.

Perhaps the information provided by Wolfram will help you: Cubic Formula .

Part 1: About the same time that I discovered how to modify a function as to only affect a single output, I also discovered a way to produce the following sequence using only elementary operators {+, -, *, / and ^}: {1, 1, 2, 2, 3, 3, 4, 4, etc...} I do realize that a solution could be found using the floor and ceiling operators, but that will not be accepted for the answer. As in my first challenge, you are only allowed to use addition, subtraction, multiplication, division and exponents. No other operators are allowed. Also the function is restricted to the set of integers. Because the domain can be shifted to start with whatever input you choose, I will accept any solution that produces the above sequence that only uses the elementary operators stated previously. Part 2: I will also give a five star rating and reputation to the person who can give me a single solution for the following sequences where the values are repeated according to [math]2^x[/math]: {1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, etc...} {1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, etc...} {1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, etc...} The solution that I am looking for in this case uses the elementary operators as stated for part 1 in conjunction with the series operators, [math]\Sigma[/math] and [math]\Pi[/math]. I will also accept a solution using [math]\Sigma[/math], [math]\Gamma[/math], factorials, or Pochhammer. I will give this challenge a few weeks before posting the solution unless someone solves it or requests more time : )

One more hint... The modification must produce zeroes for all inputs except [math]f(3)[/math] which must produce [math]\pi - 9[/math].

It can be quite a challenging problem. But, it will make you smile once you figure it out . Plus, the simplicity of the solution is actually quite impressive for what it actually does. The main hint in the problem is that the domain is restricted to the set of integers. Plus, the output [math]\pi[/math] is as arbitrary as the input 3. I figured you already made that determination. I made this statement for others who are trying to solve this problem. I'm going to go watch a movie. I'll check back periodically : ) One more thing.... I did not use the modulo operator or modular arithmetic ; )

You are allowed to assume anything, except piecewise functions, as long as it only uses elementary operators. Otherwise, I solved this problem using only addition, subtraction, multiplication, division, and powers. Oh, and of course, the variable [math]x[/math].

I'm sorry Schrödinger's hat, but I only used elementary operators. No Calculus, or any higher mathematics except Algebra. I'll give you a hint in that the input, 3, is an arbitrary value. I could've chosen any integer value for the input.

The modification that I am looking for only makes use of elementary operators (+, -, *, /, ^) and nothing more. I did not use a piecewise function, series operators, trigonometry, or any other higher operators. I do realize that it seems impossible, but I assure you that it can be done using simple math.

I'm sorry I didn't cleary define the rules. I actually thought about stating that one could not just define [math]f(3)=\pi[/math], but I figured that was obvious enough. Also, I will not accept any form of interpolation or piecewise functions. The answer is actually quite simple. However, it takes a little thought. It took me about 2 hours to figure it out when I first thought about this problem. But, I had been working on similiar problems at the time : )

A long time ago, I discovered how to modify a function in such a way as to only affect a single output for a given input. The function's domain is restricted to the set of integers. The following is an example of what I am describing: [math]f \colon \mathbb{Z} \rightarrow \mathbb{R}[/math] defined by [math]f(x)=x^2[/math] Without affecting any other output of [math]f(x)=x^2[/math], can you figure out how to modify the function such that [math]f(3)=\pi[/math] ? The modified equation must still produce all other outputs of [math]f(x)[/math] and only change the output of [math]f(3)[/math] such that it would produce the following sequence (ignoring negatives in the example): {..., 0, 1, 4, [math]\pi[/math], 16, 25, 36, ...} If you have read this post carefully, you might be able to figure out the missing piece: [math]f(x)=x^2 \, + \, ?[/math] I will post the answer at the end of the week unless someone solves this problem or requests more time : ) Edited to state the rules: You cannot define [math]f(3)=\pi[/math] or use piecewise functions. You can only use addition, subtraction, multiplication, division, exponents, and the variable [math]x[/math] and nothing else. No higher order operations such as series operators, trigonometry, etc.. is allowed (This includes modular arithmetic).

A nuclear fission reactor.

I never stated that it actually predicts all of the primes. I stated that it generates primes. Sorry, I wasn't clear on that. But being a generator of primes, it is very interesting.

I have found something very interesting on generating prime numbers: http://www.primenumbersformula.com/ I have checked the equations using Mathematica and so far they do produce primes. I would like to see what you guys have to say about these equations. Also, the links to your site aren't working. So I can't see the math you are doing.

First of all you need to check your math: [math]\frac{4\, m}{340 \, m/s} \ne 0.011 \, s[/math] Then, you will need to know how to set up the proper equation: You have the distance - [math]4 \, m[/math] You have a value for the speed of sound through air (use the value the homework specified) - This is what Wikipedia gives [math]343.2 \, m/s[/math] at [math]20^\circ C[/math] You know how to derive the time in seconds given a distance and a velocity - [math]s=\frac{m}{m/s}[/math] you know that it takes longer for the sound to travel through air. So, you would then know that [math]Air_{(time)} \left(\frac{m}{m/s}\right) - Material_{(time)} \left(\frac{m}{m/s}\right)=\Delta t[/math]. Next, you are looking for the speed of sound through the material where the change in time between pulses is [math]\Delta t=11 \, ms=0.011\, s[/math]: [math]\frac{4\, m}{343.2 \, m/s} - \frac{4\, m}{X \, m/s} = 0.011 \, s[/math] Finally, it is up to you to solve for [math]X[/math].

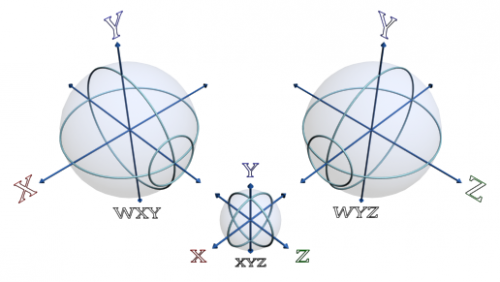
To try and explain it better Michel, it is not the galaxies, stars, or planets that are expanding. Rather, it is the space between the galaxies that is expanding. The mathematics is based on a four dimensional sphere that is growing in size which represents the space that is expanding. The clocks are not expanding. Their size remains constant. We can break the four dimensional sphere into two, three dimensional, spheres that combine to represent the "bubble" of space that we exist in. The surface of one sphere represents the XY plane and the other is the YZ plane. Because the overall four dimensional sphere is expanding, these three dimensional spheres are also expanding. The effect is such that we perceive an expanding space with no center for the expansion. If we could somehow see four dimensional space, we would see that there is a center which is located at time zero. I have created the following image to demonstrate the concept: The image decomposes the four dimensional sphere into two, three dimensional spheres labeled, WXY and WYZ. The middle, XYZ, sphere is a result of combining the XY surface of the WXY sphere with the YZ surface of the WYZ sphere. The smaller circles on both, WXY and WYZ, spheres demonstrate the portion of the two spheres which combine to make our three dimensional "bubble". Please note that this image is not drawn to scale as it would be impossible to accurately show the relationships. Also, I have not labeled the W axis as it could lead to confusion because it is very difficult to render four dimensional space. One might misinterpret the W axis as being perpendicular to itself when combining the WXY and WYZ spheres when in fact it is the same axis for both spheres. The image is intended to show how we lose the W axis as a result of how we perceive a four dimensional sphere that is expanding at the speed of light. I hope this clarifies any confusion with this system and to how the mathematics was derived.

I don't think that it would be proper to think of this as a scaling system. The clocks remain the same size as the sphere is getting larger. You could think of the clocks as getting smaller, but there is no need for both to scale in size. If the sphere and the clocks both expanded, then the space surrounding the clocks would never eventually flatten out. Time Dilation Before we continue this discussion it is important to note that I have choosen natural units for the speed of light in the equations from the previous posts such that [math]c=1[/math]. This is a result of parameterizing the equations such that the photon traverses the length, [math]L[/math], in the interval [math]u=0[/math] to [math]u=1[/math]. I'm sorry I didn't mention this in the previous posts. I've just had other things on my mind lately. I realized that I omitted the fact that I had used natural units in my graphs and in deriving the time dilation equations when I reviewed my notes. This means that all positions, velocities, and accelerations are proportional to [math]c[/math]. We can rewrite the equations such that [math]c=1[/math], and undo this naturalization once we have derived our equations. We will also use the arc length integral to derive the length of the path and ultimately the time dilation equation: [math]\int_{0}^{1}\sqrt{w'(u)^2+x'(u)^2+y'(u)^2}\, du[/math] where [math]w(u)=\left (W_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]x(u)=\left (W_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]y(u)=\left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (W_{\gamma}\right ) \, \sin(\Delta \theta_{y})[/math] We will use the simplifed version of the above equation and we will not consider acceleration as previously stated: [math]w(u)=\left (\Delta W\right ) \cos\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]x(u)=\left (\Delta W\right ) \sin\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]y(u)=\left (\Delta W\right ) \sin\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] Time Dilation - W Axis This post is only going to look at deriving time dilation for motion along the W axis. We will derive time dilation along both the W and X axis in the next post. Since we are not going to be changing our X position, our equations simplify to the following (Note: [math]c=1[/math] so it has been removed due to using natural units, also we are not considering acceleration): [math]w(u)=\Delta \tau\left (\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0\right ) \cos \left (\pm \frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right )[/math] [math]x(u)=0[/math] [math]y(u)=\Delta \tau\left (\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0\right ) \sin \left (\pm \frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right )[/math] Now that we have the equation in the form that defines motion with uniform velocity along the W axis, we can simplify the terms inside the square root of the arc length integral (Note: I have factored the result and arranged the terms so that we can easily derive time dilation in the following steps): [math]w'(u)^2+x'(u)^2+y'(u)^2=\Delta \tau^2 \left ( \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\mathit{Vl}_w^2\right )[/math] Next we will undo the natural units for the speed of light: [math]\Delta \tau^2 \left ( \frac{\left(\frac{\mathit{Vl}_w}{c} \left(2\, n+1\right ) + 2\, \frac{\mathit{Wl}_0}{c}\right)^2}{\left(2\, \frac{\mathit{Vl}_w}{c} \left(n+u\right ) + 2\, \frac{\mathit{Wl}_0}{c}\right)^2}+\left(\frac{\mathit{Vl}_w}{c}\right)^2\right )=\Delta \tau^2 \left ( \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\left(\frac{\mathit{Vl}_w}{c}\right)^2\right )[/math] Finally, we can substitute this result into the arc length integral and factor out [math]\Delta \tau[/math]: [math]\Delta \tau \int_{0}^{1}\sqrt{ \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\left(\frac{\mathit{Vl}_w}{c}\right)^2}\, du[/math] Now that we have the length of our path, we can easily derive the time dilation equation: [math]\Delta \tau \left(\int_{0}^{1}\sqrt{ \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}-\left(\frac{\mathit{Vl}_w}{c}\right)^2}\, du \right)^{-1}[/math] Because the curvature of a sphere diminishes as it gets larger we must include [math]\mathit{Wl}_0[/math] as it does affect the radius of the sphere. We can also show that this time dilation equation for an expanding sphere approaches those in SR as time approaches infinity. This can be done by evaluating the limit as our integer multiple of [math]\Delta \tau[/math], or the variable [math]n[/math], approaches infinity: [math]\lim_{n \to \infty}\Delta \tau \left(\int_{0}^{1}\sqrt{ \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}-\left(\frac{\mathit{Vl}_w}{c}\right)^2}\, du \right)^{-1}=\Delta \tau \left(\sqrt{ 1-\left(\frac{\mathit{Vl}_w}{c}\right)^2}\right)^{-1}[/math] That concludes tonights post. I have some serious family matters to attend to, so I will not be able to conclude the discussion on time dilation until next week.

I made this post to "entertain" the possibility of FTL in response to the "possible" discovery at CERN. Also, I originally created this thread in the speculation forum back in July 2011. It is not that I choose to ignore you Pincho Paxton. I simply have not considered an Aether. So any response that I could make would most certaintly be ignorant of your ideas.

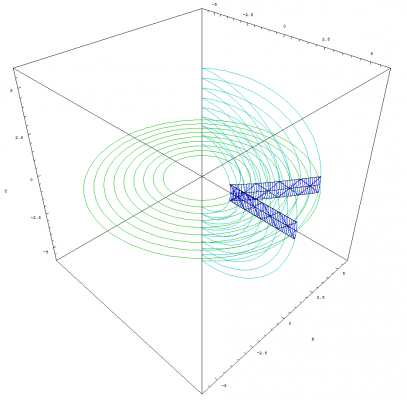
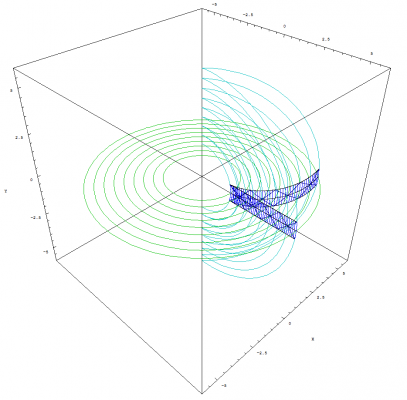
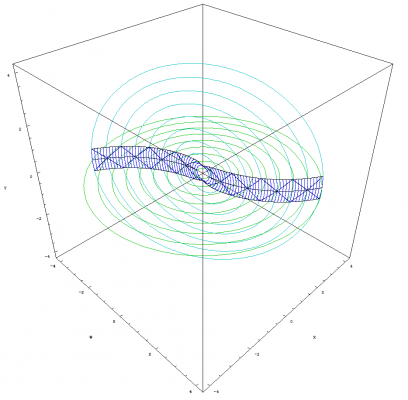
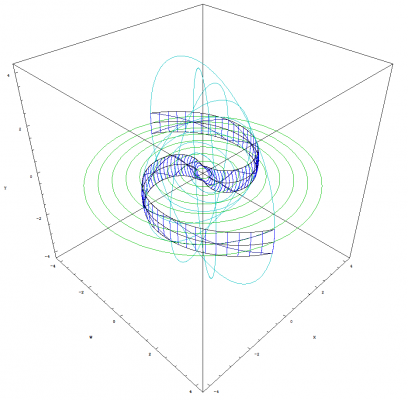
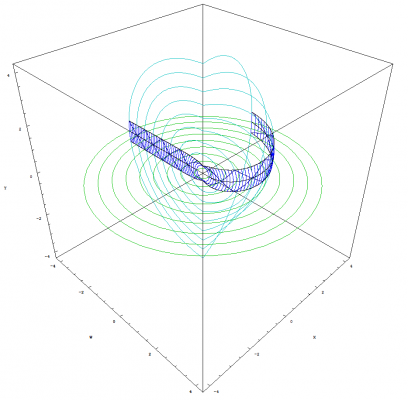
Hi Michel, I can render some different views of the graph for you. But I will try and explain what you are seeing. 1.) Mathematica renders the graphs inside a box. I can remove this box if you like. It is only there to show the axes and provides a ruler. 2.) I'm sorry about that effect. I simply set the view such that the axis lined up that way. It removed a lot of clutter while keeping certain lines that I wanted to display. 3.) The green and aqua rings represent the expansion of the sphere which are growing at a constant velocity. Those rings also can be viewed as temporally displaced views. The blue strips, which represent the clocks, encompasses those triangles structures you are talking about. I can remove all of the reference points around the trianglular paths if you like. They are there to show you how everything stays aligned with the sphere. If you look at the triangle structure in the blue strips, they are getting wider and wider for the images that show acceleration. The acceleration you see in the above graphs does not mean that the 4D sphere is expanding at an accelerated rate. The sphere is expanding at the speed of light. It is the clocks, that are traversing across the surface of this expanding sphere, that are accelerating as shown in most of the images from the previous post. I also forgot to mention that I plot the up and down path of photons for each clock. That is why you see the diamond shape paths inside the blue strips.

I thought I would post an update to this thread in regards to a possible finding at CERN which may have actually found neutrinos that moved faster than the speed of light. This finding is still being analyzed by physicist and is currently being talked about here at ScienceForums.net in the following thread: Faster than lightspeed achieved? I will quote Swansont regarding this finding because he has made an excellent point: With that being said, I would like to discuss the point I have made in this thread regarding a hypothetical correction to the Lorentz factor. This correction was meant to imply that it is impossible for length to contract to zero, but it can also allow for the possibility of a particle to travel faster than light. I am not suggesting that the mathematics proposed here is correct or that the physicist have in fact confirmed this finding. Instead, I am making this post to entertain the notion of how a particle could move faster than light using the proposed mathematics. My proposed modification to the Lorentz factor: [math]\gamma=\sqrt{1-\frac{v^{2}}{c^{2}}\times (1-l^{2})}[/math] We know that SR has a value for [math]l[/math] which is equal to zero. However, if [math]l\ne 0[/math] then a particle could hypothetically move faster than light: [math]\gamma=\sqrt{1-\frac{v^{2}(1-l^{2})}{c^{2}}}[/math] We can clearly see that if [math]l\ne 0[/math], it would act to reduce the numerator in [math]\frac{v^{2}}{c^{2}}[/math] and allow for higher relative velocities than [math]c[/math].

As promised Michel, here are some more images that show how bodies remain temporally aligned. This image shows one clock moving away from the other at a constant velocity: This image shows one clock accelerating away from the other: This image shows both clocks accelerating along what we perceive to be the X axis: This image shows both clocks having a ridiculously extreme acceleration:

I was just making a joke Neo : ) But, I am sorry about what you are going through and it is good to see that you are making the best of a bad situation. Even though I haven't been sick, I could say that the past 2 years has been the worst years of my life because I lost everything in my divorce which came after I was laid off of a 91K / yr job. However, I feel as you do. I've never been as close to my family as I am now, and I am free to do as I please. I was married / enslaved for 15 years : ( But, she did give me some of the best things I have in life... my two wonderul sons.

I also agree with Pantheory. My belief is that a universe cannot exist without mathematics and that mathematics would not exist without the universe. I have given a more detailed explanation of that statement in my theory of temporal uniformity on page 2 posting #37. The point of the statement is that all things mathematical must have existed at time zero or before the birth and expansion of our universe. Since everything in Physics is based upon a mathematical model, gravity must have also existed at time zero or before our universe came into being.

That definitely gives me something to think about. Hi Michel, the following image shows the clock that is moving outward with positive time, accelerating along what we perceive to be the X axis: That is why I labeled this section, "On The Temporal Uniformity of Accelerating Bodies". We clearly see that all bodies will remain temporally aligned regardless of thier motion. The point I am trying to make is that time dilation is not some form of temporal displacement that allows us to disappear from our view of the universe and reappear at a point in the future. Time dilation only slows down or speeds up clocks. As stated before, all clocks work by some form of oscillation. The effect that we perceive to be a dilation of time, is nothing more than our atomic processes slowing down or speeding up which does effect our motions and aging process. That is how time dilation is viewed in Temporal Uniformity. I will post more images tonight that demonstrate accelerating bodies : ) Tommorow we will begin to discuss time dilation. We will only include velocity and not acceleration as defined in SR. After we have covered time dilation, I will post detailed images of the spiraling singularity and we can discuss its properties.

Next time you feel like giving some of that money away, I'd be more than obliged to take it off your hands : )