Daedalus

You are most definitely pardoned Pantheory : ) I made that reference to SR because I have not yet considered gravity except in stating a hypothesis about temporally displaced mass-energy that could explain dark matter and galactic rotation curves. But as you and I have discussed, Temporal Uniformity does have something to say concerning the Big Bang. The next step is to either tackle gravity / GR or attempt to relate Temporal Uniformity to QM. I personally feel that integration with QM is the next logical step because I believe the solution regarding gravity will emerge as a result. However, I do not have illusions of grandeur in that I will achieve this step or that the work I have done thus far will be considered "Nobel Prize" material. But like many of us who pose theories, I do hope that the work I am doing will, in some way, prove to have merit. It is on that note that I would like to extend an invitation to everyone who has the knowledge and is willing to be a part of developing this theory to join in on the fun : ) I would also like to thank AJB, Michel123456, and you Pantheory for all of the support you guys have given me as well as Klaynos and Swansont for debating the topic. I absolutely agree. The main reason which sparked the idea of Temporal Uniformity was due to some of these theories regarding time and QM. My friends and I were watching "The Universe" the Saturday before Easter Sunday. It was the episode that discussed different theories of time. They were talking about the possibility of time travel when I looked over at my friend, Jim, and said "That mechanism for time travel it preposterous!". I don't quite remember which theory they were discussing, but I proceeded to explain to him why I felt that way. The next day, I began developing Temporal Uniformity and have been working on the theory in my spare time ever since.

Well put AJB, I couldn't have said it better : )

I appreciate the comment Pantheory. As you can probably tell, I managed to pick up a few things in graphic design while developing class 2 casino gaming devices. To answer your question, Temporal Uniformity by itself is currently just an extension to SR. I am researching QM to see if there is a common ground between my spiraling singularity in comparison to that of ring singularities. I found some interesting material by Don J. Stevens referring to Alexander Burinskii's model which describes electrons as naked ring singularites. Read up on what Don J. Stevens has to say about the electron as a ring singularity: Electron - Ring Singularity Granted, they may be correct or they could be wrong. But, I must consider all sources of information if I am going to find a possible link between the mathematics that I have currently produced with those of QM. To achieve this, I must consider other forces and physical constants within my mathematical model and explore many other theories in Physics.

Considering the nature of Neo's views, I figured someone would debate the subject. But I do agree with you AJB, it will not be much of a debate : ) Neo, I recommend that you read up on relativity. Documentaries on the Science Channel are fun to watch, but they do not provide you with a good foundation for which to pose theories into the nature of the universe. The link I provided you will at least give you a good place to start, but you will need more than just Wikipedia if you truly want to pose educated questions. As for your question regarding Chaos theory, you can also read about it at Wikipedia: http://en.wikipedia....ki/Chaos_theory One thing you need to consider is that you cannot have chaos without order. They are two sides of the same coin. That is why you see chaos, as you have stated, where I see balance.

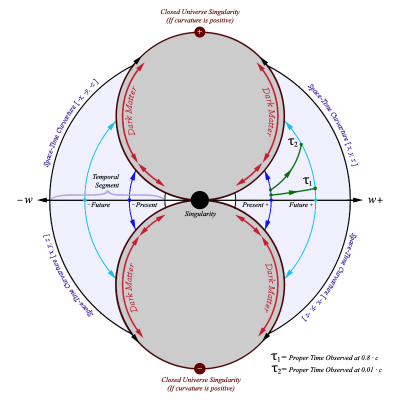
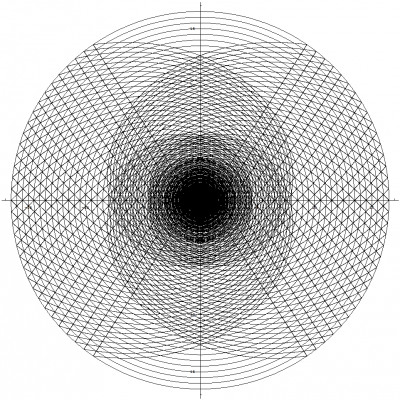
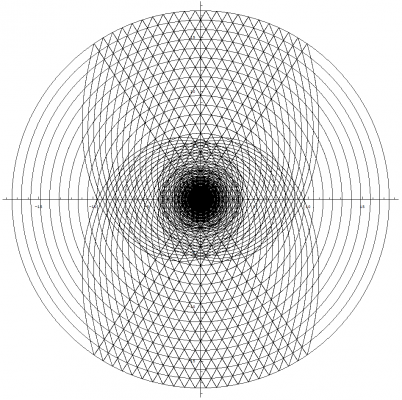
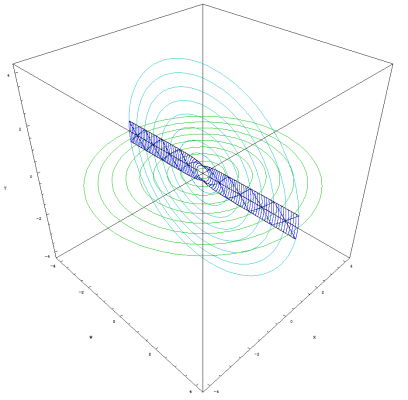
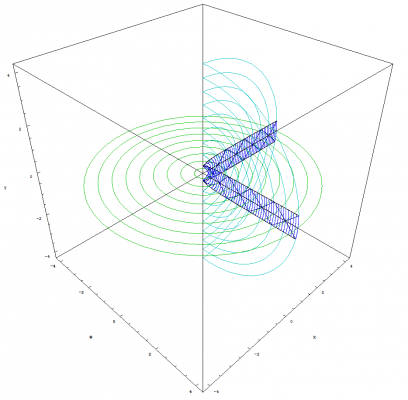
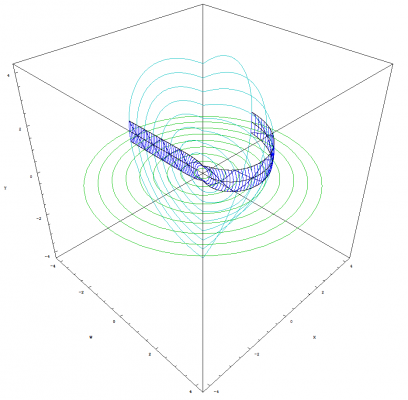
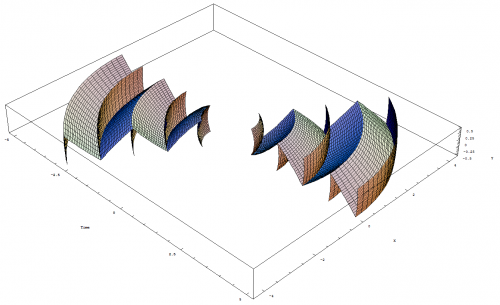
I'm glad you asked Pantheory as these equations and graphs are the result of five months of work. I developed my idea for Temporal Uniformity April 24th, 2011 on Easter Sunday. I opened Photoshop and began to draw the image that I had imagined would explain the phenomena of time and made a hypothesis that dark matter could be temporally displaced matter that caused gravitional effects in our view of the universe. Temporally Uniformity states that regardless of a bodies motion, that body will remain temporally aligned with all other bodies. The graphs from the previous post demonstrates this concept (especially if you look at the image that demonstrates acceleration). The graphs also demonstrate that the space-time vector for all observable bodies, with the tail at the center of the expansion and the head located at the body's current position, is equal in magnitude as demonstrated by graphing two or more clocks. The mathematics and graphs also show that, from our view of the universe, all three observable dimensions of space would appear to be expanding. The image showing one clock that is moving [math]90^\circ[/math] from the other illustrates this concept. A better example of this expanding space would be to plot two clocks that have a smaller angle between them. The image below was created before I had derived any of the equations for the theory. You can see that my equations and graphs fits pretty close to what I was trying to achieve by comparing the above image to the image I have graphed by combining multiple light clocks as seen below. Except, I have only considered the constancy of the speed of light. The above image is soley produced by graphing multiple photon paths, that are radiating outward with the expansion, and by removing the restriction on the parameter, [math]u[/math], so that the path is allowed to continue beyond the boundaries of the reflective plates in the light clock. The rings are reference points as stated previously and can also be thought of as temporally displaced views of the universe. We can also see that the equations produce a spiraling singularity at the center of the expansion. I have rendered detailed graphs of this singularity and we will discuss this topic once we have concluded deriving the time dilation equations. The mathematics also allows for a time before the expansion and, by working backwards from time zero, I produced the following image showing the path of photons flowing inward into the spiraling singularity. I never intended for the mathematics to produce the singularity. My goal was to derive time dilation equations for a path across an expanding sphere so that I could make a post about how we can derive such things for spaces other than flat Euclidean space. You can only imagine my excitement when I was able to produce the mathematics and graphs, based on my original image, that seem to support my ideas. I hope this explanation clarifies as to why I have developed this mathematical model and how it fits within the framework of Temporal Uniformity.

lol... you are too much Neo : ) Although, I will say that you can expect some debate on your [math]e=m\, c^2[/math] busted theory.

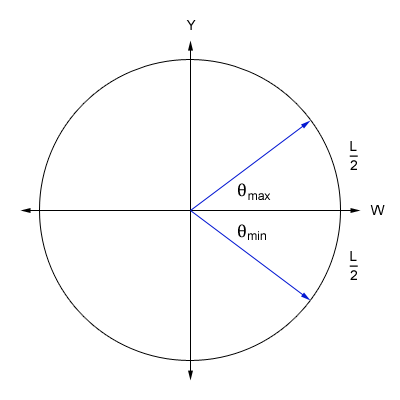
We discussed the equations for describing the angles and path in the previous post, but we really didn't define the path for the photon or parameterize the equations. So we will start by discussing how we will define this path, and the mathematics needed to parameterize the equations. The above image allows us to visualize the problem. We can see that I have positioned the arc of length [math]L[/math] so that it is centered along the horizontal W axis. This bisects the arc into two parts of equal length. We do this so that we can simplify the maximum and minimum angles (shown in blue) that the photon traverses for both, the up and down paths. Using the equation from the previous post that defines the angles, we can calculate the maximum and minimum angles as follows: [math]\theta_{max}=\frac{L/2}{r}=\frac{L}{2\, r}[/math] [math]\theta_{min}=-\frac{L/2}{r}=-\frac{L}{2\, r}[/math] We know that the photon will traverse the length of the arc at the speed of light. The amount of time it takes for the photon to traverse this distance is [math]\Delta \tau[/math] as we have previously discussed. But instead of defining the equation for the change in angle as [math]c\, \Delta t / r[/math], we need to parameterize the equation such that the photon starts its journey when the parameter [math]u=0[/math] and has traversed the length of the arc by the time [math]u=1[/math]. We still preserve the speed of light and [math]\Delta \tau[/math] in that the parameter, [math]u[/math], only operates within the range of zero to one. This allows us to define the equations for the change in angles of the path of the photon as follows: [math]\Delta \theta_{u}=\frac{u\, L}{r}[/math] where [math]\left \{u \in \mathbb{R} \ | \ 0 \le u \le 1 \right \}[/math] [math]\Delta \theta_{up}=\theta_{min}+\Delta \theta_{u}=-\frac{L}{2\, r}+\frac{u\, L}{r}=\frac{L\, \left (2\, u-1\right )}{2\, r}[/math] [math]\Delta \theta_{down}=\theta_{max}-\Delta \theta_{u}=\frac{L}{2\, r}-\frac{u\, L}{r}=\frac{L\, \left (1-2\, u\right )}{2\, r}[/math] As expected, [math]\Delta \theta_{down}=-\Delta \theta_{up}[/math]. We can now substitute [math]c\, \Delta \tau[/math] in place of [math]L[/math] and arrive at the parameterized equation which describes the angles that the photon traverses for both paths. We will also redefine this angle as: [math]\Delta \theta_{\gamma}=\frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}[/math] Because the photon starts at the coordinate, {w, 0, y}, we can now define the equation which describes the path of the photon. Since we only consider the horizontal W axis and the vertical Y axis in our initial coordinate, the equation is simply that which defines a circle: [math]w'=r\, \cos \left (\pm \Delta \theta_{\gamma}\right )=r\, \cos \left (\pm \frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}\right )[/math] [math]y'=r\, \sin \left (\pm \Delta \theta_{\gamma}\right )=r\, \sin \left (\pm \frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}\right )[/math] Before we can substitute this result into the equation that we derived in the previous post for the path that traverses an expanding sphere, we must also parameterize all of the equations we have previously defined. Luckily, this step is easy to accomplish as we only have to replace [math]\Delta t[/math] in these equations with [math]\left (u+n\right )[/math]. The variable, [math]n[/math], defines integer multiples of [math]\Delta \tau[/math]. This is because we need to be able to advance the up and down paths of the photon by the amount of time it takes for the photon to traverse the length of the arc. We will also be using the modified [math]\Delta \tau[/math] versions of the equations for motion where [math]\mathit{Sl}_{0}[/math], [math]\mathit{Vl}_{S}[/math] and [math]\mathit{Al}_{S}[/math] notation will be used to represent the modified constants. We finally have all of the pieces to the puzzle (not including the mechanical clock)!!! The equations which describe motion in the form of uniform acceleration ([math]\Delta W[/math] defines the radius of the sphere): [math]\Delta W=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right )[/math] [math]\Delta X=c\, \Delta \tau\left (\mathit{Xl}_0+\mathit{Vl}_x \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_x \, \left (u+n\right )^2\right )[/math] [math]\Delta Y=c\, \Delta \tau\left (\mathit{Yl}_0+\mathit{Vl}_y \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_y \, \left (u+n\right )^2\right )[/math] The equations which describe the angles as the clock traverses across the expanding sphere (take note that [math]c\, \Delta \tau[/math] is canceled out as a result of the division): [math]\Delta \theta_x=\frac{\Delta X}{\Delta W}=\left (\frac{2}{2}\right ) \frac{\mathit{Xl}_0+\mathit{Vl}_x \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_x \, \left (u+n\right )^2}{\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2}=\frac{2\, \mathit{Xl}_0+2\, \mathit{Vl}_x \, \left (u+n\right )+\mathit{Al}_x \, \left (u+n\right )^2}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] [math]\Delta \theta_y=\frac{\Delta Y}{\Delta W}=\left (\frac{2}{2}\right ) \frac{\mathit{Yl}_0+\mathit{Vl}_y \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_y \, \left (u+n\right )^2}{\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2}=\frac{2\, \mathit{Yl}_0+2\, \mathit{Vl}_y \, \left (u+n\right )+\mathit{Al}_y \, \left (u+n\right )^2}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] The equations which describe the coordinates for the untransformed path of the photon (Describes what we perceive to be a stationary clock that is only moving through the temporal dimension): The photon path angles: [math]\Delta \theta_{\gamma}=\frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, \Delta W}=\frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] The untransformed path of the photon (+ angles describe the up path and - angles describe the down path): [math]W_{\gamma}=\Delta W \cos \left (\pm \Delta \theta_{\gamma} \right )[/math] [math]Y_{\gamma}=\Delta W \sin \left (\pm \Delta \theta_{\gamma} \right )[/math] or [math]W_{\gamma}=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right ) \cos \left (\pm \frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}\right )[/math] [math]Y_{\gamma}=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right ) \sin \left (\pm \frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}\right )[/math] The equations which describe the coordinates for the transformed path of the photon: The full non-simplified version: [math]w'=\left (W_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]x'=\left (W_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]y'=\left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (W_{\gamma}\right ) \, \sin(\Delta \theta_{y})[/math] The simplified version with [math]\Delta \theta_{w}=0[/math]: [math]w'=\left (\Delta W\right ) \cos\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]x'=\left (\Delta W\right ) \sin\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]y'=\left (\Delta W\right ) \sin\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] We can also specify initial angles from which to start the path. This modification is very easy to do as shown below: [math]w'=\left (\Delta W\right ) \cos\left (\Delta \theta_{x}+\phi_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] [math]x'=\left (\Delta W\right ) \sin\left (\Delta \theta_{x}+\phi_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] [math]y'=\left (\Delta W\right ) \sin\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] Images produced by graphing the equation: The rings that are seen in the images below are only used for reference points. The paths of the photons are the triangle like structures. The arcs that can be seen along with the photon paths are all of length [math]L[/math]. We can see from the images that this mathematical framework models space in such a way that it will eventually appear flat as time approaches infinity. This image shows two light clocks. One is moving outward with positive time and the other is moving outward with negative time (see page 2 posting #34 for an explanation of positive / negative time): This image shows one clock moving outward at [math]90^\circ[/math] from the other: This image shows acceleration in the clock that is moving through positive time (please note that I used extreme values for the acceleration so that I could produce this very cool image): This image shows a multitude of clock paths: This image is very interesting indeed as we get our first glimpse of the spiraling singularity: Next, we will use the completed equation and derive time dilation. After we have derived the time dilation equation, I will describe the singularity and post detailed images that I have graphed of it. Good night everyone. I hope that you all have enjoyed reading this thread, reviewing the mathematics, and looking at the images of the graphs : )

Thank you for the reference Pantheory. I will try to make time ; ) to explore all of the many theories that discuss time. I have considered what you have said about time in regards to an interval of change. I must conclude that you and I are debating two sides of the same coin. I have referred to motion in many of my posts as a mathematical description of a rate of change. Mathematics is purely abstract in that any motion is described as a rate of change. I relate this concept to the reality or concreteness of our universe as pure physical motion. With that being said, one can argue that both of our concepts are balanced through opposition and are one and the same no different than up is to down. So I will concede and define that time is as you specify, "an interval of motion / change" as these are both one and the same. One being mathematically abstract, the other realized in a concrete / physical sense. P.S. I was browsing the forums when I seen you posted. You can expect my e-mail tomorrow when I wake up as I will not post the remainder of the mathematics for another day or so to allow everyone to view and interpret the math. This will give you some time to review what I have derived so that you can prepare your responses to what I will post and how you might be able to use it in your theories.

I am going to let my posting tonight stand for a day or so. But, I will be more than happy to send you an e-mail of what I have so far as I do have your e-mail address. Right now my brother is demanding that I go and jam on the guitar with him, but I will send it to you as soon as I can : )

You are welcome Pantheory and I also agree that time can best be understood and explained by definition alone. However, temporal uniformity is not just concerned with explaining the phenomena of time. The purpose of the mathematical framework that is being set forth is to redefine the Lorentz factor and show how we can begin to explain even more complex phenomena as a result. The mathematics and graphs that I will be posting may be of some interest to you as they do produce vortices. I understand that your latest thread, Pushing Gravity, deals with such things in the aether.

I am familiar with the phenomenon, aberration of light. The mathematics set forth does not conflict with this phenomenon as our space is practically flat as supported by the mathematics. Perhaps we can discuss this phenomenon in detail after I have presented this mathematical framework to see how well it fits vs. observation or we can start a new thread regarding that discussion. Also, could you please edit your quote of my latest post to not include the entire posting as you are only referring to my repsonse to your statement. Thank you : )

That is correct Michel. The concept that I have been examining is that where a four dimensional sphere is expanding through all dimensions. Perhaps I wasn't clear in explaining how we perceive this four dimensional sphere. But to try and respond to your statement, it is true that we are enclosed locally in an expanding three dimensional sphere. The 4D distance that you are referring to, only explains why massive bodies do not speed up or fall behind us temporally. If this 4D distance was not uniform for all observable bodies, then these bodies would either appear or disappear from our view of the universe. Continuing with the discussion, we now have to define the parametric equation that describes a path across that of a sphere. For this we must use trigonometry. Before we can define this equation, we must start by defining a line segment as an arc that traverses across the surface of the sphere. The equation for the length of an arc across a sphere with radius [math]r[/math] can be derived as follows (We will simplify this example by examining a circle): The circumference of a circle is given by: [math]2\, \pi \, r[/math]. The angle, in degrees, encompassing the arc is proportional to [math]360^\circ[/math] where [math]\frac{\theta^\circ}{360^\circ}[/math] defines the percentage of the circle that the arc traverses across. This allows us to calculate the length of the arc by multiplying the circumference of the circle by this ratio: ArcLength or distance, [math]d=\frac{2\, \pi \, r\, \theta^\circ}{360^\circ}=\frac{\pi \, r\, \theta^\circ}{180^\circ}[/math] Now that we know how to calculate the length of an arc, we must solve for [math]\theta[/math]. This is because [math]\theta[/math] changes as a body traverses across the sphere or circle. [math]\theta^\circ=\frac{180^\circ \, d}{\pi \, r}[/math] We can simplify this result by converting degrees to radians (When referring to an angle from this point on we will always be using radians as it truly simplifies the mathematics): [math]\theta_{rad}=\left ( \frac{\pi}{180^\circ} \right ) \frac{180^\circ \, d}{\pi \, r}=\frac{d}{r}[/math] We discussed the equations for motion in the previous post and can now substitute that result for the variable, [math]d[/math], in the above equation which describes the angles that such motion produces as a body traverses across the sphere. The hypothesis states that this sphere is expanding at the speed of light. This means that the radius, [math]r[/math], of the sphere is expanding at the rate [math]c[/math]. However, we will substitute [math]V_w[/math] because it represents the temporal velocity that we have been discussing since the beginning of this thread. We will also define the motion of this expanding sphere no different than how we have defined motion in the previous post. This results in allowing temporal acceleration for completeness. However, this does not imply that we accelerate through time as it is hypothesized that this temporal acceleration, [math]A_w[/math], is now equal to zero. The reason for including it is so that we can experiment with inflation which states that the universe expanded faster than the speed of light during its initial birth as hypothesized by Alan Guth in 1980. If inflation did in fact occur, then it would be possible to have temporal acceleration. However, we will not be discussing inflation at this time. It is important to understand that our measurement of time in this mathematical model is nothing more than a count of cycles as provided by some form of clock. We can convert these cycles to seconds by using a conversion factor, frequency, as previously discussed. This results in mathematical time as being calculated by taking the distance travelled and dividing it by the speed at which such distance was traversed. With that being stated, it is still proper to define time with the variable, [math]t[/math], which is equivalent to: [math]time=\frac{cycles}{frequency}=\frac{meters}{meters / seconds}[/math] Combining everything discussed, we can now derive the equation which describes [math]\Delta \theta[/math] for a body as it traverses across the surface of an expanding sphere. We will use the standard equation for uniform acceleration from which we will substitute our modified [math]\Delta \tau[/math] version in later. The equation which describes the motion along the axis S: [math]\Delta S=S_0+V_s \, \Delta t+\frac{1}{2}A_s \, \Delta t^2[/math] The equation which describes the motion of the expansion of the sphere: [math]\Delta W=W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2[/math] The change in angle that such motion produces as a body traverses across the expanding sphere: [math]\Delta \theta_s=\frac{\Delta S}{\Delta W}=\frac{S_0+V_s \, \Delta t+\frac{1}{2}A_s \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] Now that we can calculate the [math]\Delta \theta[/math] for such motion we can define the parametric equation which describes the path of the body starting from the coordinate, {w, 0, y}: [math]w'=w \, \cos(\theta_{yaw}) \, \cos(\theta_{pitch})\, -\, y \, \cos(\theta_{yaw}) \, \sin(\theta_{pitch}) \, \cos(\theta_{roll})\, +\, y \, \sin(\theta_{yaw}) \, \sin(\theta_{roll})[/math] [math]x'=w \, \sin(\theta_{yaw}) \, \cos(\theta_{pitch})\, -\, y \, \sin(\theta_{yaw}) \, \sin(\theta_{pitch}) \, \cos(\theta_{roll})\, -\, y \, \cos(\theta_{yaw}) \, \sin(\theta_{roll})[/math] [math]y'=y \, \cos(\theta_{pitch}) \, \cos(\theta_{roll})\, +\, w \, \sin(\theta_{pitch})[/math] The coordinate, {w, 0, y}, is the starting position of the photon that travels between the reflective surfaces of the light clock. The angle, [math]\theta_{yaw}[/math], is a rotation about the vertical Y axis and describes the angle that changes as the clock traverses what we perceive to be the X axis. We will redefine [math]\theta_{yaw}[/math] to be [math]\theta_x[/math] to avoid confusion between which angle causes horizontal translatory motion along the X axis. The angle, [math]\theta_{pitch}[/math], is a rotation about the horizontal X axis and describes the angle that changes as the clock traverses what we perceive to be the Y axis. We will also redefine [math]\theta_{pitch}[/math] to be [math]\theta_y[/math] to avoid confusion between which angle causes vertical translatory motion along the Y axis. The angle, [math]\theta_{roll}[/math] is a rotation about the W axis. We will redefine [math]\theta_{roll}[/math] to be [math]\theta_w[/math] as it defines the angle of rotation for the mechanism in a mechanical clock as will be discussed much later. The above parametric equation is derived by multiplying the rotation matrix for each axis in a specific order that describes the angles as yaw, pitch and roll. The equation can also be derived by applying the following equation, which describes the rotation of a point about a specific axis, in the same manner as the matrices: [math]x'=x \, \cos(\theta)\, - \, y \, \sin(\theta)[/math] [math]y'=x \, \sin(\theta)\, + \, y \, \cos(\theta)[/math] Now that we have our equations which describe the changes in angles and the path across a three dimensional sphere, we will end this post with the following summary: The equations which describe motion in the form of uniform acceleration: [math]\Delta W=W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2[/math] [math]\Delta X=X_0+V_x \, \Delta t+\frac{1}{2}A_x \, \Delta t^2[/math] [math]\Delta Y=Y_0+V_y \, \Delta t+\frac{1}{2}A_y \, \Delta t^2[/math] The equations which describe the angles as the clock traverses across the expanding sphere: [math]\Delta \theta_x=\frac{\Delta X}{\Delta W}=\frac{X_0+V_x \, \Delta t+\frac{1}{2}A_x \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] [math]\Delta \theta_y=\frac{\Delta Y}{\Delta W}=\frac{Y_0+V_y \, \Delta t+\frac{1}{2}A_y \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] The parametric equation which describes a path across the sphere: [math]w'=w \, \cos(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, y \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, y \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]x'=w \, \sin(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, y \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, -\, y \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]y'=y \, \cos(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, w \, \sin(\Delta \theta_{y})[/math] The next posting will complete the mathematics presented in this post by deriving the equations which predict the coordinates that a photon in the light clock traverses for both the up and down paths. I will also be posting images of the graphs that these equations produce for the path of the photon. We will discuss [math]\Delta \theta_w[/math] when we get to the point where we are describing the path for a mechanical clock. For now, we will set [math]\Delta \theta_w=0[/math]. Once we have completed the mathematics which describe the path that light from a light clock takes as it traverses the expanding sphere, we will substitute our equations for motion that make use of [math]\Delta \tau[/math] and derive the time dilation equation. Please keep in mind that even though I have made great effort to ensure that the mathematics that I have posted is correct, I have been known to reverse and mix things up from time to time. Also, my grammar isn't the best in the world : ) Everything that I have posted has been graphed and verified using Mathematica. With that being said, please message me if you do find an error so that I can make the appropriate corrections. Thank you.

On The Temporal Uniformity of Accelerating Bodies The view that is to be set forth attempts to describe the universe from the point of view of a four dimensional sphere that is expanding at the speed of light. We can simplify the equations by breaking this sphere into two, three dimensional, spheres. This results in one sphere being comprised of W, X and Y axes, and the other dealing with W, Y and Z axes. The W axis is the spatial dimension of time and is shared along with the vertical axis, Y, between both spheres. If one considers that we exist on the surface of such spheres, then we can take a section of each sphere and combine them to form our three dimensional view of the universe. The spheres would be aligned such that one sphere provides the X, Y plane and the other provides the Y, Z plane. Because the curvature of a circle or sphere diminishes as the radius increases, and due to the enormous size of these spheres, our space will appear to be flat. Also, we would lose the W dimension because the four dimensional sphere is expanding at the speed of light and length contraction would have collapsed the fourth dimension to have no perceivable length. For the sake of simplicity, we will only consider the W, X and Y sphere. This will allow us to derive time dilation equations across what we perceive to be a two dimensional plane. The purpose of exploring time dilation for the path of a clock as it traverses across the surface of an expanding sphere is to derive the mathematics for the Lorentz factor which is affected by such surface which is not flat. We will explore the paths for a light clock and a rotating mechanical clock and show that both approach the equation for time dilation as defined in SR as time, and subsequently the radius of the sphere, approaches infinity. The equations that are to be discussed are not new and by no means considered complex as they simply deal with the basic mechanics for motion as defined in classical physics. The equations that will be discussed will include uniform acceleration and we will begin by discussing Newton's interpolation formula as it allows us to derive a single equation for simple motion that is only dependent on the locations of a body along its trajectory. This allows us to extend the equations for motion beyond that of uniform acceleration. Newton's interpolation formula can be written using the binomial theorem as follows (The locations of a body's trajectory combine in such ways that use binomial coefficients when interpolating such simple motions. We can also use the Gamma function to generate these coefficients): [math]\sum_{i=0}^{n-1} \left [ \sum_{j=0}^{i} \left [ \left ( -1 \right )^{j} \binom{i}{i-j} S_j \right ] \times \binom{i-t-1}{i} \right ][/math] The variable [math]n[/math] is the number of measurements or specified locations, [math]S_j[/math] is the location specified by the [math]j[/math] index, and [math]t[/math] is time. It is important to note that the locations are sampled within equal intervals of time. As a bonus, I will post the interpolation formula for locations sampled at any given time once we have completed this journey : ) If we let [math]n=1[/math], the formula yields the initial position [math]S_0[/math]. When [math]n=2[/math], the formula yields the equation for motion as defined by the initial position and velocity: [math]S_0 +\left (S_1 - S_0\right )t[/math]. Finally, we can derive the equation for uniform acceleration by specifying [math]n=3[/math] which yields the following: [math]S_0 + \left (\left (S_1-S_0\right ) - \frac{1}{2} \left (S_2-2\, S_1+S_0\right )\right ) t + \frac{1}{2}\left (S_2-2\, S_1+S_0\right )t^2[/math] We can see from the above results for [math]n=3[/math], that we can easily derive the constants for acceleration and velocity as follows: [math]a=\left (S_2-2\, S_1+S_0\right )[/math] [math]v=\left (\left (S_1-S_0\right ) - \frac{1}{2} \left (S_2-2\, S_1+S_0\right )\right )[/math] However, this does not help us derive time dilation as we need to define acceleration, velocity, and the initial position in terms of the time it takes for light to travel between the reflective surfaces of a light clock that are separated by a length [math]L[/math], or the distance [math]\left \vert AB \right \vert[/math]. This results in redefining the locations, [math]S_j[/math], in terms of [math]L[/math] such that [math]S_j=\mathit{l}_j \times L[/math] where [math]\mathit{l}_j[/math] is a length scalar or multiple of [math]L[/math]. The amount of time it takes light to travel between the two reflective plates of a light clock is equal to [math]\Delta \tau = L / c[/math] such that [math]L = c \, \Delta \tau[/math]. Substituting this result back into Newton's interpolation formula allows us to completely factor out [math]c \, \Delta \tau[/math] as follows: [math]c \, \Delta \tau \sum_{i=0}^{n-1} \left [ \sum_{j=0}^{i} \left [ \left ( -1 \right )^{j} \binom{i}{i-j} \mathit{l}_j \right ] \times \binom{i-t-1}{i} \right ][/math] We can now reconsider the constants of acceleration, velocity, and initial position when [math]n=3[/math] as follows: [math]a=c \, \Delta \tau \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )[/math] or [math]a=c \, \Delta \tau \ a_l[/math] where [math]a_l=\left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )[/math] [math]v=c \, \Delta \tau \left (\left (\mathit{l}_1-\mathit{l}_0\right ) - \frac{1}{2} \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )\right )[/math] or [math]v=c \, \Delta \tau \ v_l[/math] where [math]v_l=\left (\left (\mathit{l}_1-\mathit{l}_0\right ) - \frac{1}{2} \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )\right )[/math] and [math]S_0=c \, \Delta \tau \ \mathit{l}_0[/math] [math]S_1=c \, \Delta \tau \ \mathit{l}_1[/math] [math]S_2=c \, \Delta \tau \ \mathit{l}_2[/math] It is important that [math]\Delta \tau[/math] is completely factored out. Otherwise, it will get trapped inside the parametric equations which describe the path that light from a light clock takes as it traverses across the expanding four dimensional sphere and we would not be able to derive time dilation accordingly when using the arc length integral to calculate the length of the path. The usage of Newton's interpolation formula to describe simple motion will only be used in this post as we will only concern ourselves with uniform acceleration. The reason for discussing this equation was so that we can establish a foundation for which simple motion of any form, including that beyond uniform acceleration, can be used to derive the time dilation equation and ultimately the Lorentz factor. Next, we will apply the equation for uniform acceleration to a light clock that is traversing across an expanding sphere. But, that is for the next post.

I'm sorry StringJunky. I made that post late last night and hadn't really edited what I wrote. But, thank you for paragraphing it for me : )

It has been a while since I have been able to browse the forums but I feel that I must comment on this particular topic as I have made good money in ordering chaos to produce casino gaming devices which brings us to your topic of life being random or predictive in nature and the odds of such things occurring. While there is no simple answer to why life has formed and why it seems to be so rare, one cannot make an argument for whether it is random or predictive as both are two sides of the same coin. It is impossible to define order without its opposite, chaos, no different than up is to down. Making a statement that life on Earth has had a "lucky" streak that seems impossible implies that you understand the rules of the game that life is based upon and as far as I know we are still working on figuring that out. You are refering to all of the mechanisms that must be in place for life on Earth to exist while dismissing that creation and destruction both drive the mechanism of life. An asteroid impact my indeed sterilize the Earth but it may also combine organic molecules into structures that spawn a new era of life that may be similiar to ours or different based upon the chemistry that is formed and the laws that govern evolution. It is the laws that govern life and evolution that make life "predictive" or ordered as you suggest, but it is also the randomness of such things that give us variety and allow for such things to come into existence. Some may argue that our universe is such that we hit the jackpot and physics allows for such things as complex organisms to evolve to question their own existence while others will cling to a creationists point of view. But in the end, it takes both predictability and randomness to make life work. Without randomness our world may not have even formed as all worlds would have a predictable outcome which may not have included our Earth, but without predictability life would not be able to adapt to a completely random universe that is constantly changing in the short term. You state that the odds for this lucky streak the Earth has experienced is to good to be random and you are partially correct IMHO. However, you cannot dissmiss the role randmoness plays in our universe. Even though I control the odds in every casino game that I have created, I cannot control when such plays occur or how the player will experience the result. Given enough time, my games will play out to how I design them within a given tolerance. Regardless of how improbable I set the odds for the jackpots in my games they do occur. But that by no means suggests that the Earth came into being by design. Instead, it would seem that life is a deliberate act of randomness that is guarenteed to occur given enough time.

Perhaps you are correct Pantheory and time is nothing more than an interval of change. However, I ask you to consider what is change? We typically think of change as an explanation for why something is different than how it was, but this does not clearly define why something changes or how it has changed. If we dig deeper into the mechanism of change, we will find physical motion as the cause. This can be demonstrated in that a change in a body's position is caused by the motion of the body relative to our own position. The erosion of a landscape is caused by the motions of matter and energy as it applies forces upon the land that it is acting upon. Even when considering sources of change that do not seem to have motion, such as that of the wave of colors produced by electrochemical processes in a cuttlefish, there is always an underlying mechanism which is in motion that produces such change. The colors in our clothing fade due to exposer to photons and chemicals which strip the pigments from the material. I can continue to list many more examples of things that change. The point is that we will always find that it is actual physical motion that drives change. That is my reason for not accepting that time is just an interval of change because it is physical motion that drives change and not change that drives physical motion. If we take the example where we can define time by dividing the distance traveled by the speed at which we traversed such distance and then place ourselves in the rest frame where our displacement and speed equals zero, then when we try to determine our time we get a division by zero which is undefined. One could state that this is a relative matter but we are still left with mathematics for which only works if we are in fact in motion relative to something else. This mathematical paradox of an undefined time for the rest frame of reference can only be resolved if we consider that we are always in motion through the dimension of time and that we do indeed traverse a physical distance through this fourth dimension. I now have internet and my ISP has provided me with web space to upload the images I have created so that we can continue this discussion and explore the mathematics that I have derived as explained earlier in my posts. I understand that this mathematical framework does not assure that the theory is correct, nor does it mean that temporal uniformity will gain acceptance by my peers as Swansont has pointed out. However, a theory without a mathematical basis is forever doomed to failure as it cannot provide us with a means to check the validity of such theory. A good theory not only provides us with definitions that describe the mechanics of the universe, but provides us with the means to rule it out by checking its assertions as provided by the mathematics. I will start by breaking the mathematics into simpler components from which I will make seperate posts describing the mechanics of each component. Once all of the equations have been defined I will assemble them together and post the images that they graph along with a link to the Mathematica file that I have produced so that everyone with Mathematica 5.2 or greater can reproduce the graphs and images. We will begin the discussion this week once I have set up my web space and have uploaded the images and files that I will be posting : )

Sorry I haven't been active in a long time. I have everything ready to post but I cannot find a site that will host the images so that I can link them directly to my posts. If someone knows of a good site that will allow me to upload the images so that I can link them here, I would appreciate it. Otherwise, I will have to wrap everything up in a PDF file and upload it to Google Docs so that I can provide a link.

Thank you for changing the thread title MooeyPoo. I just didn't want this thread to be confused with the "time" poll thread or its author.

When you consider that motion can be defined as frequency times meters per cycles, or: [math]f \frac{m}{cycles}[/math] We can clearly define the mechanics of time as a statement of the total distance traveled divided by the distance traveled within an interval of oscillation where frequency is the time conversion factor and cycles represent our measurement or unit of time. Let's say that we traveled 3 meters within one interval of oscillation as provided by a pendulum. The pendulum is not tuned to oscillate within an interval of a second and therefore each oscillation is a measurement of time of its own temporal unit as provided by the pendulum. We can use a conversion factor, frequency, to convert the cycles of the pendulum to seconds, but this is not as important as the distance traveled within the interval of oscillation. If our speed remained constant, and we lost our pendulum, then we could divide the distance traveled as stated by our odometer, with the fact that we travel 3 meters within the interval of oscillation and derive the time, in units of the pendulum's cycle. 300 meters divided by 3 meters / cycle equals 100 cycles of the pendulum. If the frequency of the pendulum was tuned so that one cycle equals one second, or frequency equals one, then a total of 100 seconds would have passed for the 300 meters we traversed. In essence, any measurement of time is actually a statement of the total distance traveled divided by the distance traveled within an interval of oscillation. Since we know from the equations of relativity and that of temporal uniformity, that we move through the fourth dimension of space at the speed of light, then we can use an oscillator and calculate the distance traveled through this fourth spatial dimension. The same principles work for all other observable spatial dimensions as stated previously and as shown in the above example using the pendulum. The equations and plots that I will be posting in a week or two, clearly demonstrate these principles. I have successfully derived time dilation in accordance to the path that light from a light clock traverses across an expanding four dimensional sphere. I have checked my new equations against the equations for time dilation in special relativity. My equations produce near identical results and converge to the equations of relativity as our distance through the fourth dimension, or time, approaches infinity. This is a result of the diminishing curvature of a sphere or circle as it gets larger and larger. The equations also produced something that was unexpected, a singularity that spirals towards time zero of the big bang. This is a result of light racing around an extremely small sphere that has just started to expand. As time progresses, the light can no longer complete the journey around this expanding sphere due to the size of the sphere itself. This results in the light path tapering off from a spiral to progressing in straight lines away from the singularity as the universe expanded. Also, I have calculated the maximum viewing angle, based on the speed of light, that we can see across this expanding sphere. This results in our space as being an isolated three dimensional sphere that is expanding away from the Big Bang at the speed of light. Granted, I have not considered any other physical forces or constants except that of the speed of light. However, I will make a conjecture that this spiraling singularity should form a ring singularity once these forces are added into the equations and QM affects are considered. Also, one must consider Occam's razor which suggests that we should tend towards simpler theories which provide explanations regarding the subject matter at hand. This does not imply that my theory of temporal uniformity is correct, but instead shows that we should consider temporal uniformity because it provides simple explanations for all phenomena of time which is based on the accepted theory of relativity.

I have been extremely busy getting ready to go back to OU this fall. I do not have internet at the moment and am using a friends computer to post this message. I have more of the mathematics worked out and I will post the results as soon as I get moved into my new apartment. Everything has been done with Mathematica and I will post the equations and images of the plots so that you all can reproduce my results. I must say that you guys are in for a real treat : )

Olvin, I never got to see your original documents. I will read through the one you posted, so I can understand what you are describing.

Ok I couldn't resist. I will give you guys a hint. I better not .

Swansont, I do realize and respect the arguments that you have made in regards to QM and time. I appreciate you taking time to debate the topic. I hope we all have a little better understanding of what time may be. The question is definitely not answered with 100% certainty. But if we do discover temporally displaced mass-energy, then this will have huge implications. A huge part of my theory uses Bose-Einstein condensates. Check out this discovery made by physicist at the University of Bonn in Germany. I hypothesize that the singularity at the heart of every black hole is a super-photon or Bose-Einstein condensate of mass-energy in some form. Since we know that light is related to electron - positron pairs at high energies, then it could be possible that the singularity is actually a matter Bose-Einstein condensate associated with an anti-matter Bose-Einstein condensate. Once black holes throughout the entire universe consume all of the mass and energy, space collapses and causes all of the black holes from the center of galaxies to come back together at time zero at the center of the big bang. This falls in line with the principles of temporal uniformity because of the hypothetical Einstein Rosen bridges, or wormholes that may exist inside supermassive black holes linking two or more points in three-dimensional space or through the [math]w[/math] axis of space-time. The warping of space due to all of this mass-energy would cause these two condensates, at the center of the singularity, to collapse into each other resulting in another big bang. The condensates could form in a similiar manner as shown in the experiment that the physicists at Bonn have conducted. Except the massive pressure induced by the collapsed space inside the singularity provides the cooling effect as it restricts the motion of particles or waves allowing for the condensates to form. However, this third part of my theory is purely speculative. But, it does allow us to derive a theory of quantum gravity that is based on GR, QM, and temporal uniformity. Once I have created such model, I will be able to determine the validity of these extended claims unless the hypotheses I made towards dark-matter is observed in star wobbles, giving validation through observation. Considering the consequences of this view, it may be possible that Hawking radiation does not evaporate supermassive black holes at the center of galaxies. The virtual anti-particles caught in the event horizon that fall in would either be absorbed by the anti-matter condensate, or if it collided with the matter condensate it would just be converted back to light and be split up between both matter and anti-matter condensates where the process repeated in a chain reaction until this new mass-energy was distributed equally. This would work identically for the virtual matter particles. We could also further hypothesize that any form of mass-energy transforms into a super-photon that splits into matter / anti-matter pairs due to the acceleration from falling towards the singularity. This would allow both matter and anti-matter condensates at the heart of the singularity to always be balanced and it provides an explanation for the cause of the big bang. Therefore, infinity is expressed through recursion in cycles of big bangs and the finite quantity of space-time and mass-energy is conserved. Thus my general theory of temporal uniformity pretty much relates all things that exist in the abstraction of mathematics to the reality of our concrete physical universe and even though it may be wrong, it appears to be balanced. Since no one has pointed out why it is incorrect or proved it wrong, then my claims stand. I would be happy to retract my claims in light of other truths. It does not mean that I would abandon the theory altogether. It just means that I could align my thought process towards the facts and derive new hypotheses accordingly. I make this conjecture towards supermassive black holes because the current accepted theories tell us micro black holes will evaporate. However, we cannot ignore the implications of what it would mean if my view is correct and that we cannot destroy a singularity once it has been created. This means that the LHC could actually end life on Earth due to micro black hole creation which may not actually evaporate. Not to be superstitious but 2012 is next year and the LHC keeps increasing the levels of energy used in collisions. However, the scientist predict that it will be 2014 before the LHC runs at full power and current theories support black hole evaporation. I just want to end with this; "extraordinary claims require extraordinary evidence", Carl Sagan. I have actually constructed a device that is very extraordinary and it is not an anti-gravity device or anything as such. But once the patents go through, I can reveal what it actually is and it is quite remarkable. I believe it embodies everything I have debated to be true and the evidence that it does exist is hard to deny.

Point taken and well made. I didn't mean to actually imply that you agree with my theories. My intention was to show how scientists are looking for a more accurate and precise metric for space-time and to point out that my theory aligns itself along this view.