Daedalus

Eureka!!! I just proved the Collatz conjecture to be true!!! I' m in total disbelief, and I'm sure you all are as well, but I can finally prove it! However, since I'm a software engineer and not a mathematician, I'm sure any paper that I write would be inadequate at best. If my proof is verified to be correct, then such a paper needs to be written and structured correctly. What should I do? This is a tremendous opportunity to involve our community here at SFN to help me produce a paper and get it submitted to a respectable journal but, since the forum is not a journal and is open to the public, I risk someone else claiming my ideas as their own if share them here. Since it would take me a long time to learn everything I need to know to tackle such a paper, perhaps it would be better for me to hire a mathematician to write the paper on my behalf. What do you all think I should do? I'm almost done writing my proof in Mathematica and I really want to post it.

Yeah there is the tasty human consideration, but I think that would be unlikely as they would most definitely have an established food chain and meals that don't involve human burgers with a side of fries. Don't forget that they evolved on a planet and, just like us, would most likely enjoy having a home with a view where radiation and decompression wasn't a concern. Sure, but that's covered by my first post because such contact is peaceful. Given our medical technologies and advances in nanotechnologies, it's most likely that aliens have solved the biological and medical problems associated with coming into contact with life that has evolved independent from their own. They would most likely have nano tech that allows them to exist in most toxic environment and combat bacteria and viruses. I'm sure we wouldn't set foot on a planet without the tech to keep us alive and healthy, and the same things apply to them.

I think it's highly unlikely for a "District 9" situation to occur. Yes there is a chance of that happening, but any species that is capable of traveling intergalactic distances will have the technology to sustain such a journey. Therefore, it is most likely that if aliens did come to Earth, they would most definitely have the ability to wipe us from the planet. If they came here in peace, after seeing how we behave, I'm sure they would limit the contact their people have with ours. I'm pretty sure we can make some reasonable speculations. Given our own technological achievements, it's safe to say that any species that has achieved the ability to travel intergalactic distances (from one star system to another) would have computational and robotic technologies to mine and harness resources from any planetary sized or smaller celestial body. With these technologies, it would be easier to obtain needed resources from places where humans don't exist than it would be to come to Earth and try to barter for them or take them from us by force and, because they would be able to get any resource Earth provides from any other body orbiting the sun, we can safely say that the likelihood that they have come to Earth to harvest our resources is unlikely. That is, of course, assuming that aliens haven't come to Earth for a place to live. Of course, aliens might have discovered that we exist and want to make peaceful contact, but for that to be the case they either had to be close enough to us for enough time to have passed for our radio broadcasts to have reached them, they reached a point in space to where they could detect us, or they have telescopes powerful enough to determine that we exist without needing to detect our radio signals. Although all of these cases are possible, it's most likely aliens would come here looking for a new home. It makes perfect sense. Since we can determine the chemical composition of an exoplanet's atmosphere, we can conclude that aliens would have better technologies to do the same thing. If Earth meets all the requirements for life on their world, then surely they'd want to spread their species throughout the galaxy. It's evolutionary suicide to only stay on one planet when you can travel intergalactic distances. Furthermore, because of resource demands, we would never launch a mission to just any solar system without having a good reason to go there. Aliens would also have the same requirements. So, we can safely speculate that if aliens did come to Earth, they intended to come here regardless if they knew we were here before they left or not. The only other thing to consider in this view is if they need the Earth and / or if they are willing to fight us for it if we did not want them to live here.

Congratulations Fatih!!! The equation you derived is absolutely correct, and you definitely have mathematical ability! I truly believe that if you love mathematics, then you should definitely pursue it regardless of what your teacher or anyone else thinks of you (shame on your teacher for saying you're an idiot). I started out doing the same type of mathematics that you have demonstrated here in this thread and it grew into a love for the subject that allowed me to explore and discover new mathematics (new to me anyway). Even if the equations that you discover are already known, the fact that you took the time to figure them out for yourself places you far ahead in the game. Don't let anyone deter you from doing the things you love. As for your equation: Given [math]m[/math] rows and [math]n[/math] columns of 1x1 squares where [math]m \le n[/math], we can construct [math](m-1)[/math] rows and [math](n-1)[/math] columns of 2x2 squares, [math](m-2)[/math] rows and [math](n-2)[/math] columns of 3x3 squares, and so forth until we reach [math](m-m+1)[/math] rows and [math](n-m+1)[/math] columns of [math]m[/math] x [math]m[/math] squares. Using the upper limits and working backwards, we can show that there are [math](1)(n-m+1)[/math] number of [math]m[/math] x [math]m[/math] squares, [math](2)(n-m+2)[/math] number of [math](m-1)[/math] x [math](m-1)[/math] squares, [math](3)(n-m+3)[/math] number of [math](m-2)[/math] x [math](m-2)[/math] squares, and so forth such that for any [math](m-i+1)[/math] x [math](m-i+1)[/math] sized square where [math]1 \le i \le m[/math] there are a total of [math](i)(n-m+i)[/math] squares. To find the total number of squares in the [math]m[/math] x [math]n[/math] rectangle, all we have to do is sum [math](i)(n-m+i)[/math] on the interval [math][1,m][/math]: [math]\sum_{i=1}^m\,i\left(n-m+i\right)=\sum_{i=1}^m\,n\,i-\sum_{i=1}^m\,m\,i+\sum_{i=1}^m\,i^2[/math] Find the polynomial solutions for each sum: [math]\sum_{i=1}^m\,n\,i=\frac{n(m)(m+1)}{2}[/math] [math]\sum_{i=1}^m\,m\,i=\frac{m^{2}(m+1)}{2}[/math] [math]\sum_{i=1}^m\,i^2=\frac{m(m+1)(2m+1)}{6}[/math] Simplify the resulting algebra: [math]\frac{n(m)(m+1)}{2}-\frac{m^{2}(m+1)}{2}+\frac{m(m+1)(2m+1)}{6}=\frac{m(m+1)(3n-m+1)}{6}[/math] Proving that the total number of squares in a [math]m[/math] x [math]n[/math] rectangle of 1x1 squares is defined by the equation: [math]\frac{m(m+1)(3n-m+1)}{6}[/math] The following image demonstrates the process for a [math]6 \times 10[/math] rectangle: Number of 6x6 squares equals [math]1 \times 5 = 5[/math] Number of 5x5 squares equals [math]2 \times 6 = 12[/math] Number of 4x4 squares equals [math]3 \times 7 = 21[/math] Number of 3x3 squares equals [math]4 \times 8 = 32[/math] Number of 2x2 squares equals [math]5 \times 9 = 45[/math] Number of 1x1 squares equals [math]6 \times 10 = 60[/math] Total number of squares in a [math]6 \times 10[/math] rectangle is equal to [math]5+12+21+32+45+60=175[/math] or [math]\frac{6(6+1)(3(10)-6+1)}{6}=175[/math] When [math]m=n[/math] we get back the polynomial for [math]\sum x^2[/math] as expected: [math]\sum_{i=1}^m\,i^2=\frac{m(m+1)(3m-m+1)}{6}=\frac{m(m+1)(2m+1)}{6}[/math]

I took the time and solved this problem. However, it does sound a lot like homework. So, I'm going to guide you through how to set up the problem, but you will need to do the math. Without considering the area for the base of the cone, what can you determine about the remaining area? If we look at a 2d cross section of the cone and cylinder cut through the center, we get the following image: Now, the equation for the area of the cone minus the base, or the lateral surface area of the cone, is equal to [math]\pi[/math] times the radius of the cone [math]\left(r+x\right)[/math] times the length of the slant or the hypotenuse of the large triangle shown in the image [math]\left(\sqrt{x^2+h^2}+\sqrt{y^2+r^2}\right)[/math]. [math]A_L(x,y)=\pi r l[/math] Plugging in all of the variables yields the following equation: [math]A_L(x,y)=\pi \left(r+x\right) \left(\sqrt{x^2+h^2}+\sqrt{y^2+r^2}\right)[/math] Now, there is a trigonometric relationship that you need to use. From the image, we know that: [math]\frac{r}{y}=\frac{x}{h}[/math] Using this trigonometric relationship, you should be able to solve for [math]y[/math] in terms of [math]x[/math] (or vice-versa) and substitute that result into the equation for the lateral surface area of the cone and arrive at an equation in one variable ([math]r[/math] and [math]h[/math] are constants). From there, you need to find the minima of this equation by taking the derivative and setting it equal to zero and solving for [math]x[/math] or [math]y[/math] (whichever variable you used during substitution). Once you know the value of the singled out variable ([math]x[/math] or [math]y[/math]) , you can solve for the other variable and arrive at the answer. I've set you on the path, now all you need to do is the work. I'll help if you get stuck, and I can even check your results, but it would be best if your worked the math.

You're welcome!

I'm not 100% sure about question 1 and, since I'm at work right now, I can't research the question, but I already provided you the answer to question 2: So yes, if you give us a set of points, we can use Lagrange interpolation to find the minimum degree polynomial that goes through them, which is unique. Let me demonstrate Lagrange interpolation: [math]S(i,j)=j-\frac{1}{2}\left((-1)^{\frac{\left\vert j-i \right\vert+j-i}{2}}+(-1)^{\frac{\left\vert j-i+1 \right\vert+j-i+1}{2}}\right)+1[/math] [math]\mathcal{L}(x)=\sum_{i=1}^n \left(y_i\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] Given a set of points that are clearly cubic, [math]\{\left(1,1^3\right),\left(2,2^3\right),\left(3,3^3\right)\}[/math], the polynomial produced by Lagrange interpolation is of degree 2 instead of degree 3 as one would expect: [math]\mathcal{L}(x)=6x^2-11x+6[/math] As we can see, if you plug in the values of [math]x[/math] from the points in our set, we get back the corresponding values of [math]y[/math]: [math]\{\left(1,1\right),\left(2,8\right),\left(3,27\right)\}[/math] I attached a Mathematica 7 file that demonstrates Lagrange interpolation using the above points. LagrangeInterpolation.zip

The bridge does use steel beams as can be clearly seen in the following image.

Actually, it's more complicated than you can imagine. Swansont, Phi for All, and the other moderators and admins use the infinite improbability bot that was created by Klaynos to detect sock puppet accounts. And that is how the admins and moderators detect sock puppet accounts.

I'm not sure what the standard is, but we do seem to have a problem with trucks hitting our bridges. I can't seem to find the pic, but a few years back we had a truck get stuck under the bridge because the trailer wouldn't fit. Here's one that happened in Tulsa, OK: http://www.newson6.com/story/18992207/truck-gets-stuck-under-railroad-bridge-near-downtown-tulsa Here's another one that happened in OKC: http://www.news9.com/story/29546329/semi-stuck-under-railroad-bridge-near-downtown-okc I found the one that I was talking about: http://okcfox.com/archive/semis-continue-to-get-stuck-under-worst-overpass-in-the-city This happens more than it should...

Yeah, we don't have many roundabouts, but we do have a few. For some reason, Americans love building bridges and overpasses and, yes, we drive on the wrong side of the road. Actually, this bridge was hit before back in the 90's but on the other side. So yes, the structural integrity of the bridge had been previously compromised, and I'm fairly sure that our earthquakes are at least partially responsible for the degradation of our infrastructure. I remember as a kid, we never felt the earthquakes. Most people that live here didn't even know that Oklahoma was seismically active. I experienced my first earthquake, where the building actually shifted, about 5 years ago. Before that, I never had experienced the effects of an earthquake. So, that should tell you something about the increased frequency and strength of Oklahoma's earthquakes. I think that bridge uses concrete beams, but I'm not sure. Here's a better pic of the damage. Sirona and iNow (really any of my friends here at SFN), if you happen to make your way to Oklahoma City, send me a PM. I'll be more than happy to show you around and treat you to dinner. If you like hibachi, then we can eat at Musashi's (Japanese steak house). Hmmmmm.... I love hibachi

Luckily, no one was actually on the bridge.

Well, it was all but an ordinary day for me at the office. I'm the Sr. Software Engineer at Factor, and we are located on the 15th floor of one of the towers on the N.W. side of Oklahoma City. Just a few hours before it was time to leave, everyone started gathering near windows on the East side of the office because a semi-truck with some kind of heavy machinery loaded on its trailer tried to drive under a bridge that wasn't tall enough. So, I took the opportunity to take a few pics that actually made it on the news. As you can see, it collapsed the N.E. side of the bridge. Unfortunately, I'll have to take a different route to Guitar Center and Best Buy when I take my lunches. Luckily, no one was hurt. Here's a pic someone else took from the other side showing how badly the bridge is damaged. The building in the center of the image (maroon with tinted glass) is where my office is located.

I know some of these challenges are super hard and crazy, but this one really is an oversight on my previous work. The solution is so simple that if you take a look at the links I posted, there's a good chance you'll see how to solve this challenge. Any takers?

It has definitely been a weekend for solving problems that I've been working on for a few years, and this challenge is about a discovery that I made today involving interpolation and iterated exponentials or nested exponentials as I like to call them. Some of you are aware of my thread, Discoveries by Daedalus, where I prove various relationships for iterated exponentials and the nested logarithm operation that I discovered. Ever since the work I did on nested exponentials, I've been trying to find a nested / iterated exponential interpolation formula, and today I have discovered exactly that. The discovery occurred to me after making a few posts in the thread, Finding a Polynomial, where I talk about mine, Newton's, and Lagrange's interpolation formulas. This challenge is to use the equations that can be found in the above links and find at least one of the nested / iterated exponential interpolation formulas hidden within. I realize that this challenge is a tough one, but 90% of the work is already done for you. If you understand how those equations work, it's not very far leap to arrive at nested / iterated exponential interpolation. The interpolation formula must produce an equation of the form [math]f(x)=a^{\left \langle x \right \rangle} = a^{a^{x-1}}[/math] and interpolates either a linear sequential set of points or any set of points. I'll give bonus points if you find both nested / iterated exponential interpolation formulas. While I wait to see if anyone else can solve this challenge, I'm going to start writing up a paper on it Graphs of Interpolating [math]y=x[/math] Using Increasing Sets of Points Here are some graphs of using iterated exponential interpolation on increasing values of [math]y=x[/math] where [math]x \ge 2[/math]. As we interpolate more points of [math]y=x[/math], the generated iterated exponential function matches the curve better. If the last value of [math]x[/math] in the set of points used to generate the function is odd, then the output goes to infinity. However, if the last value of [math]x[/math] is even, then the equation is asymptotic to [math]y=1[/math] where it begins to follow [math]y=x[/math] along the interpolated points and then sharply approaches 1 at both ends. The equation failed for slopes less than or equal to 1/2. When we approach the slope of 1/2 from the right, we can see that the iterated exponential equations begin to oscillate wildly around [math]y=\frac{1}{2}x[/math]. The oscillations grow larger as the slope gets closer to 1/2.

Neat... I just realized a really cool relationship between the polynomial and exponential interpolation formulas. Polynomial / Summation [math]\mathcal{L}_{\sigma}(x)=\sum_{i=1}^n \left(y_i\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] Exponential / Multiplication [math]\mathcal{L}_{\pi}(x)=\prod_{i=1}^n \left(y_{i}^{\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)}\right)[/math] Because the exponential equation is the product of the terms, we can take the natural logarithm of the equation and rewrite it as [math]\mathcal{L'}_{\sigma}(x)=\text{ln}\left(\mathcal{L}_{\pi}(x)\right)=\text{ln}\left(\prod_{i=1}^n \left(y_{i}^{\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)}\right)\right)=\sum_{i=1}^n \left(\text{ln}\left(y_{i}^{\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)}\right)\right)=\sum_{i=1}^n \left(\text{ln}\left(y_i\right)\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] So, if we modify the polynomial interpolation formula [math]\mathcal{L}_{\sigma}(x)[/math] to take the natural log of the [math]y[/math] coefficient [math]\text{ln}\left(y_i\right)[/math] we can use the equation as the exponent for [math]e[/math] and get back the exponential interpolation formula [math]\mathcal{L}_{\pi}(x)[/math]. [math]\mathcal{L}_{\pi}(x) =e^{\mathcal{L'}_{\sigma}(x)}=e^{\sum_{i=1}^n \left(\text{ln}\left(y_i\right)\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)}[/math]

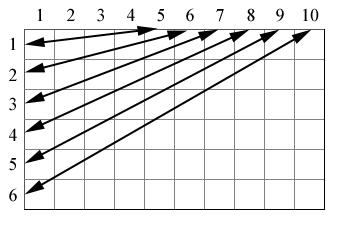
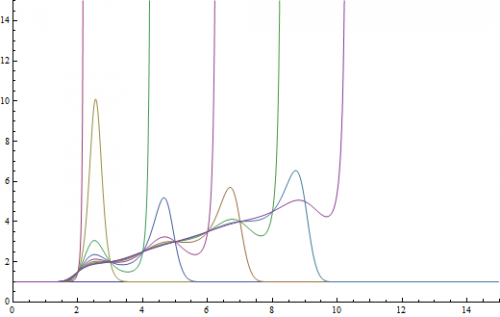
This thread brought back some old memories of when I discovered my own interpolation formulas that generate polynomials and exponential equations for sets of points. Since the topic is about finding a polynomial for a given set of points, I'll share with you all the methods that I discovered myself along with the methods that I later learned as a result of researching my own. Interpolating [math]F(x)[/math] for a Set of Points First, we need to define the function [math]S(i,j)[/math] that gives us the subscripts for [math]x[/math] and [math]y[/math] that is used by the interpolating formula to derive the polynomial. You'll notice that this function has two inputs, [math]i[/math] and [math]j[/math]. These represent the summation and product indices used by [math]\Sigma[/math] and [math]\Pi[/math]. [math]S(i,j)=j-\frac{1}{2}\left((-1)^{\frac{\left\vert j-i \right\vert+j-i}{2}}+(-1)^{\frac{\left\vert j-i+1 \right\vert+j-i+1}{2}}\right)+1[/math] When we examine the outputs of [math]S[/math] by holding [math]i[/math] constant allowing [math]j[/math] to be the variable, we see that [math]S[/math] produces a linear sequence that skips [math]i[/math] in the sequence. [math]i=1,\ j\Rightarrow \{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...\}[/math] [math]i=2,\ j\Rightarrow \{1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...\}[/math] [math]i=3,\ j\Rightarrow \{1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...\}[/math] [math]i=4,\ j\Rightarrow \{1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...\}[/math] [math]i=5,\ j\Rightarrow \{1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...\}[/math] I discovered this equation back in 1999 right after I graduated high school and was attending OU. I was interested in interpolation because when I was in high school, I discovered Newton's interpolation formula on my own and extended it to account for increasing summations of f(x). I used the knowledge gained from working that problem to create an exponential interpolation formula that works like the polynomial version except it produces an exponential equation and accounts for increasing products of the interpolated function. However, these formulas didn't work for any set of points. They had to be ordered. So, I started working the numbers and discovered the equation that interpolates any given set of points. [math]S(i,j)=j-\frac{1}{2}\left((-1)^{\frac{\left\vert j-i \right\vert+j-i}{2}}+(-1)^{\frac{\left\vert j-i+1 \right\vert+j-i+1}{2}}\right)+1[/math] [math]\mathcal{D}(x)=\sum_{i=1}^n \left(y_i(x_i-x+1)\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] The resulting polynomials always have a degree that is equal to the number of points in the set. So, my equation does not produce the lowest degree polynomial that interpolates the set of points. However, a few years later while taking Numerical Analysis at OU, I learned that my equation was actually a variation of an already known interpolation formula called Lagrange interpolation that produces the polynomial of least degree that interpolates the set of points. Interpolating [math]F(x)[/math] for a Set of Points using Lagrange Interpolation My equation was so close to Lagrange Interpolation that I only had to remove a single factor, [math](x_i-x+1)[/math], to make my equation equal to his. 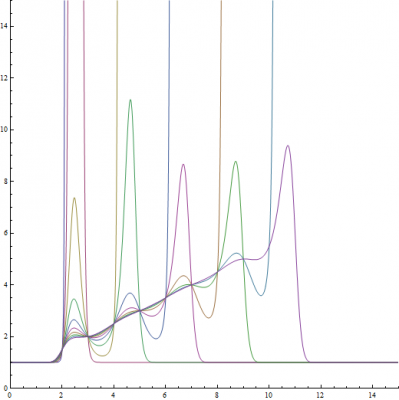[math]\mathcal{L}(x)=\sum_{i=1}^n \left(y_i\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] You can only imagine my amazement when I seen my equation staring back at me and was not only simplified, but also did something unique by producing the polynomial of least degree that interpolates the set of points. Well, I amazed myself once again when I discovered that the method I used to extend Newton's interpolation formula to exponential equations also works for Lagrange interpolation! I love mathematics!!! Extending Lagrange Interpolation to Exponential Functions for a Set of Points The work I did in high school to extend Newton interpolation to exponential functions also works for Lagrange interpolation. If we think of polynomials as summing the terms [math]F_{\sigma}(x)[/math] and exponentials as multiplying the terms [math]F_{\pi}(x)[/math], then we can easily extend interpolation formulas from polynomials to exponential functions. Polynomial / Summation [math]\mathcal{L}_{\sigma}(x)=\sum_{i=1}^n \left(y_i\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)\right)[/math] Exponential / Multiplication [math]\mathcal{L}_{\pi}(x)=\prod_{i=1}^n \left(y_{i}^{\prod_{j=1}^{n-1} \left(\frac{x-x_{S(i,j)}}{x_i-x_{S(i,j)}}\right)}\right)[/math] As we can see, sigma [math]\Sigma[/math] is replaced with [math]\Pi[/math] to multiply the terms. Then, instead of multiplying [math]y_i[/math] by the product series, we apply the exponent operation. 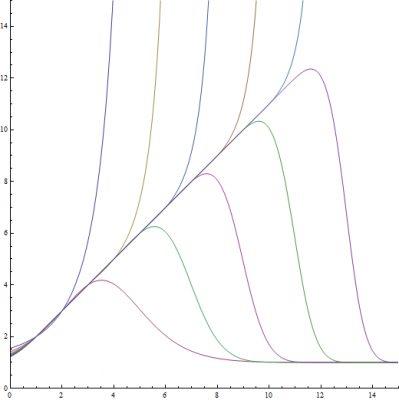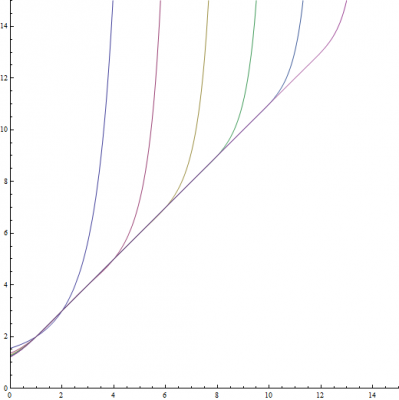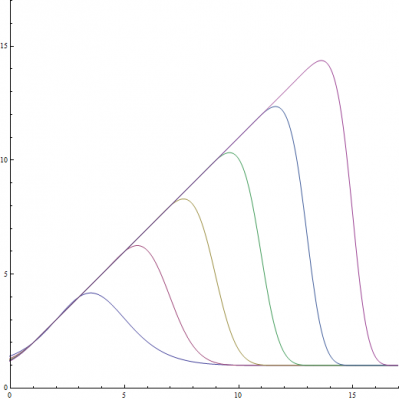Using Mathematica to Explore my Method and Lagrange's If you made it all the way to the end of this post, I have attached a Mathematica 7 file so you can play around with my method and Lagrange's. Enjoy!!! Interpolation.zip

For all the music I've written, can you set mine to be "Maestro"

You can dig through the Lounge and find them, or you can just click on the following link which takes you to my finished composition play list: https://youtu.be/BYwf3Zl9Keg?list=PLE2UaWXtygiLMeyasnGb2D17OWqu0ZlSX