Daedalus

Either you are messing with me... or you think I don't know what chords are lol... Arpeggios are chords. I was just referring to how those chords are played sequentially and not at the same time as in the way you are talking about. Standard chords are comprised of three notes separated by intervals of a third - minor third or major third in any combination e.g Augmented chord: M3 + M3, Major chord: M3 + m3, Minor: m3 + M3, or Diminished: m3 + m3. Special chords, such as Major 7th chords, contain an interval that is not found in standard chords. I also gave you credit for noticing that I didn't write any non-broken chords for a single instrument (even with the sheet music). However, the composition as whole has chordal structure and we can identify the chords played through the piece. Basically... chords are just various harmonies that accompany the melody. The different harmony structure to chords are actually model compositions of scales. The different parts of the composition could be played by a single instrument and, even though the parts can share the same note, there are parts where they form chords. Also, my keyboard died 6 years ago and I don't have a replacement. So, all of the music I write is from what I hear in my mind. ps... I just noticed you typed H,D,F... there is no H only A - G. So, it's A,D,F, which is a D minor chord in 2nd inversion

Hehehe... Thanks for the comment Sensei, but there are actual chord structures in all of my songs. I realize that you are referring to how a single instrument, such as the piano part, isn't playing what we normally refer to as chords, but the left hand is actually playing broken chords or arpeggios. When you combine all of the different instruments, the harmonies and melody do create chordal structures. This is because I write each part / voice for the instruments using different modes. Anyways, I'll see what I can do to write you something where the harmonies are played in chords on a single instrument. +1 to you for noticing!

After listening to the song for several hours, I realized that it needed to be softer is certain areas and that the piano part needed to stand out more. So, I made several adjustments and modifications, and have arrived at a very beautiful recording. Enjoy!!!

Actually Imatfaal, I was feeling a little sad over the weekend. So, I wrote this song. For myself, writing music is better than any therapy I could get.

I finished another song today. The melody is a little melancholy, and it's one of my slower pieces but still beautiful nonetheless. Enjoy!!!

I do apologoize Swansont. I didn't mean to insinuate that my ignorance was your fault. I am investing time to learn physics. Granted, it's at a slow pace, but we all have our lives to tend to and how we invest our time is on us; not you. Furthermore, I don't expect you to teach me or anyone else physics here on the forum. It would be very difficult to teach someone calculus here on the forums. However, when I reply to someone's thread, I try to be as insightful and helpful as I can, but that's me. I don't expect you to have any obligation or even find joy in trying to have a conversation about QM with someone who doesn't have all the prerequisites. I was just hoping for the kind of discussion where you might give us some inights, clues, or perhaps a lengthy conversation regarding the finer points of how atomic clocks work and why my statements are wrong. I'm currently reading and working the problems in the book, "University Physics", and I plan on getting the Feynman Lectures and a few other books on QM, but I'll start reading about spin-flip. I'm also reading material provided by Mordred. I may not fully understand it until I get a little more background in advanced physics, but I really do want to know how physics explains the universe. Unfortunately, I don't have access to the university here to perform the type of experiments that a professor would normally have the student do, but I'll manage.

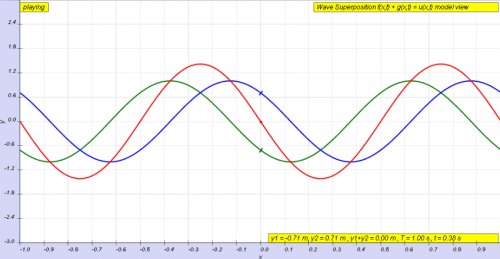
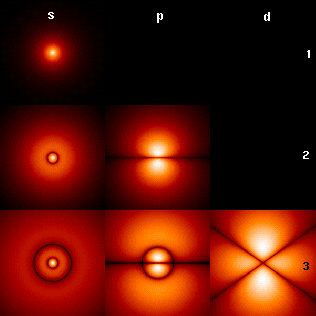
Let me clarify my definition for motion. Swansont says it's ill defined, but that's not true. In temporal uniformity motion has a very general but precise definition that encapsulates all forms of motion. Motion is simply a change in position through space, which is a measurement of distance that describes the rate of motion. [math]\text{motion} \rightarrow \Delta x[/math] However, we have to have a way to compare various motion, no different than measuring distances. If a point on a wheel or a photon in a light clock traversed [math]x[/math] units through space, I can compare that measurement of distance to the measurements of distance for objects in space that have moved around me and define a speed for each object relative to my frame of reference or coordinate system. However, we don't call these measurement of distance by what they are. Without regard to atomic clocks, the distance the clock mechanism has traversed within a mechanical clock is normallized to a unit of time that we call seconds. So, we define speed as distance over time instead of the ratio of distance an object moves through space versus the distance the clock mechanism has traversed as occurrs in actuality. The only descrepancy is to how atomic clocks work. Now, most people define motion as having a trajectory, but this doesn't encapsulate every form of motion. We cannot think of motion as being defined in the classical sense because it's relative to the observer's frame of reference. When you throw a ball through space, you see it move along its trajectory. If you placed yourself in the ball's local frame of reference, then the ball would not be moving. It would be at rest within that coordinate system. So, we simply cannot define motion as having a path. The trajectory describes a path through space, but the ball moved because it changed position relative to the observer. The path it took was a consequence of forces acting upon the ball. However, we also have motion the occurs because the shape of something is changing position through space. For instance, let's look at a waves. If you clicked on the link, you will see three waves colored blue, green, and red. The cool thing about waves, is that some of them always change position through space regardless of the frame or reference you choose. This completely defies the relativity of motion as defined in the classical sense. We are taught that the only thing that can change position through space regardless of one's coordinate system is light. That light will always move through space at the rate of [math]c[/math] regardless of your frame of reference. However, try to define a frame of reference where the red wave appears at rest. You'll find that it is mathematically impossible to do. The blue and green waves have frames of reference where the wave appears to be at rest. Define a frame of reference with the origin at one of the peaks on the blue or green wave, and it will no longer appear to change position through space. The structure of the blue and green waves is not changing position through space. However, the points in space that define the red wave always change position through space regardless of your frame of refrence, and that is motion too. The most general and precise way to define motion with regards to all forms of it is to define motion as a change in position through space. If motion does exist in QM, it would have to be wave motion. Otherwise, we could choose a frame of reference that would simply negate it, which would completely destroy the model. Regardless of our frame of reference, atoms and particles and fields exist. If we accept that motion is simply the act of something changing position through space, then we can demonstrate motion in QM relating to atomic electron transition. Here we have the definition for what it means for an electron to change from one quantum state to another where the quantume state is represented by a state vector in Hilbert space. A Hilbert space is still a complete metric space. Therefore, spatial position is defined. Atomic orbitals define the shape of the electron cloud by associating the probability of detecting an electron at a point in space. When an electrons transitions to different orbitals, the distances between like probabilities change as a result of the shape of each orbital. This is still a change in position through space even though it was the probabilities of detecting the electron in space that changed position. From the above image we can infer that different orbitals ecompass different points in space such that an electron that jumps from one orbital to another can actually change position through space. We do not have to define a trajectory to see that it can occupy points in space that were only possible after the jump was made. My conclusion is that atomic orbitals define a region in space where an electron can be detected. The only way a single electron can jump to a different orbital that defines a completely different set of points in space is if the electron itself can change position through space to occupy the different orbital. It doesn't matter if the electron teleported by some discreet distance or if it literally travelled through space. For an electron to occupy an orbit that defines points in space that were previously unobtainable or very low probaility, the electron has to change position through space to occupy the new orbital. By calculating the distance between points located on these orbitals with like probabilities, we can calculate the probabilities for the shortest or longest distances the electron can move during a jump. Given the time it takes to complete the transition, we can define probabilities for the speed at which the transition occurred. If we say the electron instantaneously jumped to the new orbital, it still changed position through space. The speed would be indeterminate but, nonetheless, a change in position through space has occurred and the electron has moved. You can say that such motion is ill-defined, but a change in position through space is all we need to infer motion. If we had a way to make an electron jump between two orbitals at a constant rate, we could take the most likely distance the electron could move during the jump, and create a clock based on QM that uses this distance to measure time no different than mechanical clocks. We can either add up this quantized distance each time a jump is made, or we can count the number of times the jump occurred. One is a measure of distance and the other is a measure of time. Both measurements can be equally used to describe processes in physics.

Oh, I am very familiar with the mathematics. The equations aren't that hard to understand. However, it's the processes working at the QM level that are a lot harder to define and describe. The mathematics of QM isn't structured like that of classical physics. Motion in QM is really not defined. So, I can't explain how the particles and fields would change position through space in an atom to cause decay, but can you? Can you describe how the energy contained within an atom gets transfered about? How it behaves? How it forms decay particles?

I might not be able to discuss the QM nature of radioactive decay, but we do know that the decay components move away from the decaying particle where such motion is a consequence of the act of decaying. However, the fact that I can use measurements of distance traversed by some mechanism instead of units of time to formulate the equation for decay is what I am discussing. See, we can easily replace measurements of time with measurements of distance. This is a very important piece of evidence. Time as measured by mechanical clocks can only do so by using some mechanism that changes position through space. There's simply no denying that with regards to classical physics that change cannot occur without matter and energy changing position through space. Otherwise, everything would be static. The real question is, as put forth by swansont, does this hold true for QM? Swansont simply says my statements aren't true within the QM world, and he really won't eloborate as to why. He says he can lead the horse to water, but that simply isn't true. When I asked why my statements were wrong, the reply given was: So, OptimisticCynics... don't hold your breath. He'll tell us QM doesn't work that way, and the horse is left thirsty for water. I would like to know why a generalization that given matter and energy the only thing it can do with respect to space is to change position is wrong with regards to QM. Classicaly, change in a system within space can only do so by stuff changing position through it. However, swansont has not elaborated as to why this is untrue with respect to QM. The problem I have with his point of "It's not [his] job to teach [us] QM" is that it's not really helpful in progressing the discussion. Why even reply to a discussion if you really aren't going to provide any input besides saying it's wrong? I am very good at math, and that would be similiar to me posting in the Calculus forum about how someone got integration wrong: OP: "Check out this new way I'm integrating the area" Daedalus: "What you are doing is wrong." OP: "Why?" Daedalus: "Integration doesn't work that way." OP: "Can you explain what is wrong?" Daedalus: "It's not my job to teach you Calculus." OP: " Then why even reply if you won't explain your statments?" Perhaps, swansont is used to dealing with people who won't accept the answers he gives them. Perhaps, the answer is way over our heads, but that doesn't mean I wouldn't investigate. I might even be able to utilize some of that knowledge to come to the same conclusions as the good doctor himself. After all, I do hold swansont in high regards even if he won't teach us QM I will continue to learn and study QM and cosmology until I can better debate my claims or retract them.

I don't think displacement is the correct term either because displacement is just a vector with the head at your current location and the tail at the origin. Although we can't define equations for motion dealing with atomic clocks and QM, we can still infer motion even if it is an "ill-formed concept". I agree with swansont that QM doesn't need to define motion in the classical sense. However, given space and "stuff" that fills it, the only thing matter and energy can do with respect to space is change position through it. Without that, then the equations of QM can't even be defined. You still need a metric space and, by defining such space, then matter and energy can only change position through it regardless of how this occurs. So, if such a concept is "ill-formed" when dealing with QM, then I can accept such a statement because logically and mathematically with respect to space the only thing this "stuff" can do is change position through it. Although I do not have a complete understanding of QM as Swansont does, our argument is pretty close to one that Schrodinger and Bohr had in Copenhagen. I absolutely love this passage from Walter Moore's book, Schrodinger Life and Thought. Like Schrodinger, I am arguing that atomic phenomena must change position through space and, although I can't describe how this would work, I also realize that we can't describe QM in the classical sense. However, my argument is not based on how this motion occurs. QM works completely different than the "old physics" because "we see the discontinuities, the jumps, quite directly in atomic phenomena". All I need to defend motion as the act of changing position through space as far as atomic clocks are concerned is the notion that given a metric space, matter and energy can only change position through space. I agree that this idea is "ill defined" with regard to how the equations of QM are derived. However, we do not need to define such classical motion to study the QM affects that arise from it. QM ignores this because we only care how the QM system behaves. This is because we simply cannot observe or derive equations of motion in the classical sense to describe quantum phenomena. However, my argument is not how motion is carried out but, given space, the only thing matter and energy can do with respect to such space is move through it. We don't need to define a trajectory; only recognize that change in a system can only occur when matter and energy changes position through space. Even though a change in position through space is "ill defined" for QM, without it, QM system would not arise. As for swansont, he approaches the argument much like Bohr. We simply can't describe such motions in a classical sense, but the equations derived by Schrodinger means that we don't have to define it in such a way. So, swansont, realizing this, defends his argument that we can't describe QM affects using motion. However, I feel like he is being as adamant as Bohr and ignores that the energy of the atom must change position through space even though the equations of QM do not define such behaviour using this classical concept but, if we redefine motion as simply the act of changing position through space, then such a definition encapsulates both classical and QM. Granted, defining how particles and energy changes position through space is "ill formed" with regard to QM, I feel that we can't dismiss it completely because, if these particles and waves do not change position through space in some way, then change in the QM will not occur. I realize that my argument will still not be satisfactory for swansont but, much like Schrodinger who never reached an agreement with Bohr, I am content with not reaching an agreement with him. Although I cannot describe such motions in regard to QM, I believe I have provided enough evidence to infer motion within QM even though it cannot be described with an equation and is therefore "ill defined".

Hehehe. I'm the Sr. Software Engineer for an oil and gas company in OKC, OK. So, I can definitely afford text books. Actually, I prefer them, and I have several regarding mathematics and software engineering. I have a few engineering physics books, but I really don't know which advanced books on physics I should get. So, I do appreciate the links and references. I plan on getting as many of those books as I can. I bought a book on tensors, but it's not easy to understand and there aren't many problems to work through. So, I'm still looking for better books on the subject.

Mordred, thank you for the material you provided. I've been reading "Infationary Misconceptions and the Cosmological Horizon" by Brian Powell, and I find it all very intriguing. Of course, I haven't read through all of the papers and links you've provided, but I do want to point out that I have stated previously that my four-dimensional spherical model is at best speculation. After reading back on what I posted in my break down that got this thread going again, I noticed that I didn't put the "speculation" disclaimer in the section, "Temporal Uniformity". Because I don't quite yet know how to use tensors to play with the mathematics of general relativity, it's easier for me to use the "balloon" model to describe how four-dimensional space accounts for our observations but, like I mentioned earlier, I fully realize that it's flawed. Once I can play with Einstein's field equations, I plan on having some fun So, I do apologize to you and everyone else for not clarifying that the 3-sphere shape of the universe in temporal uniformity is just speculation used more like an analogy to describe what we observe. The main goal of temporal uniformity is to define the nature of time in order resolve problems associated with time when dealing with "time travel". The more I began to develop the ideas regarding how we measure time using motion, the more fun it became to speculate about how four-dimensional space can be used to describe thing such as dark matter and the multiverse. However, it's mainly my statements about how we measure time and how change propagates is what I consider to be my argument. Vivec, basically what this all boils down to is how we measure things. In order to measure distance we have to use predefined distances. The same is true for anything else. We use unit masses to measure mass, and we use properties of electromagnetism to measure electric and magnetic properties. So, in order to take a measurement, we have to use the thing we are measuring. When measuring time, we find that we use motion to take the measurement. Of course, all mechanical clocks do this. However, the current discussion is whether or not we can infer motion in atomic clocks. The point is if we measure time using motion and motion is nothing more than a change in position through space, then time doesn't exist as some separate temporal dimension that's intertwined with space. So, "time travel" would be impossible because instead of three-dimensions of space and one of time, there would only by four-dimensions of space where time is a mathematical consequence of "stuff" changing position through space at finite speeds.The evidence I provide for this is based on being able to replace the time variable [math]t[/math] in every equation of physics that uses time with measurements of distance. The reason why we can replace the time variable [math]t[/math] with distance is because change only occurs when "stuff" changes position through space.

Granted, I can't describe the motion of an electron, nor can I define a trajectory, or the momentum in a classical sense, but you really can't either. QM doesn't deal with such things. It's mainly concerned with probabilities associated with other physical characteristics that describe the behavior of matter. Given how we measure properties of electrons, none of that makes any sense. How can one ascribe momentum to the probability of detecting an electron at a point in space? How could we use equations that are derived from observations that rely on such probabilities to even determine motion in a classical sense? You haven't really been paying much attention to anything I've said, or at least you are playing devil's advocate. QM came about in this discussion because I made a claim that all clocks use motion to measure the time. You can't make a mechanical clock that doesn't use motion to measure time. However, you and Klaynos introduced QM as it applies to atomic clocks because you state that QM properties of matter can't be described as motion. Of course, you are correct because measurements in QM such as those for atomic orbitals are based on probabilities. However, my argument towards clocks doesn't care about how things move. The only statement I have to defend is that change in a system can only be propagated if "stuff" is allowed to change position through space. If change can occur without "stuff" changing position through space, then my statements about measuring time with motion would be false. So, you keep hounding me to take equations that are based on probabilities to demonstrate that motion in the classical sense occurs in QM because if I can't then you have proven your point, but that's simply not true in relation to my argument at all. The fact that we have to assign a probability to a point in space where an electron might be is all I need to infer motion in QM system such as atomic orbitals. Either you find the electron at the point in space, or you don't. Surely, you can see how this infers motion? Something changed position, and really that is all that matters regarding my claim. Arguing that I have to be able to define classical motion for a set of probabilities is ludicrous, but you continue to assert your argument that if I can't define motion in QM in such way that I must be wrong. I guess we'll have to agree to disagree. It simply doesn't make sense to take billions of measurements of how many times you detected an electron at a point in space and then expect someone to define an equation using those measurements that will describe the motion of an electron in a classical way when all that is needed to support the claim is the fact that "stuff" is changing position through space. Given nothing but space and the stuff that occupies it, the only thing this stuff can do with respect to space is change position through it. So, it should be a logical conclusion that change is propagated by "stuff" changing position through it. Otherwise, how could anything interact with anything else?

You're right. I should've put more thought into my reply. When I get home from work, I'll try to come up with a better argument relating back to electron clouds. In your reply, you are still assuming that I'm viewing motion in a classical sense. I could be wrong, but it seems to me that you are cherry picking parts of my argument that falls short or is lacking while ignoring other points that I believe are valid. For instance, I have defined motion as the act of changing position through space. I haven't specified how the change in position occurs. Only that a change in position through space is motion. Given atomic orbitals, we know there is a defined shape for each orbital that represents the probability of detecting an electron at a specific point in space. Furthermore, we know that when electrons become excited, they will jump to different orbitals and then back to their original orbital releasing radiation when they do. Because they change orbitals, regardless of how they do this, the electron is changing position through space, which is motion as I have defined it. Even if you say the electron exists everywhere within this region of space, we know that when "stuff" interacts with it, the shape of this electron cloud changes. Again, I've never stated how this motion occurs, but a change in position in space is still required for the "structure" of the electron cloud to change shape. This is motion, and I have clearly stated this. However, like I said, you seem to ignore this and cherry pick only parts of the argument that you know you can dismiss, which I find surprising of you. If you haven't cherry picked things that I have stated, then why not address everything including the standing wave description or how I've stated that something doesn't have to move like a baseball because its structure, e.g. the shape of the atomic orbital, can change position through space. Lunch is over but, when I get home tonight, I will include other references that demonstrate this "motion" of the electron, which is what I intended by referencing the pop-sci article.

Well, I haven't retracted my statements. However, I'm willing to look at the evidence Mordred presented. I think that's just as important, if not more so, than trying to come up with some idea.

I'll definitely take a look at those links when I can Mordred. During the week, I don't have much time for fun stuff like this because of work, but I'll definitely check it out this weekend.

I realize those things too. My point is that we don't need to define time as some physical dimension to formulate the laws of physics. Clocks use motion to measure time, and we can replace the time variable [math]t[/math] with measurements of distance no different than I showed in my post.

I realize that energy is a property of objects. They only reason why I decided to go ahead and state energy and its various forms was to differentiate between space and the "stuff" that occupies it. I'm perfectly fine with not being able to rigorously define motion in QM. You and I both know that trying to specify an equation for the motion of an electron in an atom is a fool's errand for a novice such as myself or for any other quantum number. Besides, demanding an equation for the motion of something to prove that it moves is no different than demanding the equation for the motion of a car in order to prove that the car can change position. We simply don't need an equation to infer that such things can move or that their structure can change position through space. Furthermore, the concept of the energy contained within electrons changing position through space is studied: http://newscenter.lbl.gov/2010/08/04/electrons-moving/ I might not be able to prove that electrons move by defining an equation that predicts their motion, but I could demonstrate that they are not stationary, which infers motion. "The electrons do not orbit the nucleus in the sense of a planet orbiting the sun, but instead exist as standing waves." The structure of a standing wave actually changes position through space. "The electrons are never in a single point location". Sounds like they move around to me. I'm sorry about using Wikipedia, but I'm sure if I went down to the physics library at OU, I can get you better references and maybe even a quote from a professor. Of course, I realize this isn't a satisfactory answer to your question of motion in QM, but neither is the answer that there is no motion of any kind of structure at all. Michel123456, when considering space-time, you get time-like, light-like, and space-like intervals. However, the equation are the exact same when considering four-dimensional space. The only difference is the [math]c\,\Delta\,t[/math], which is a distance, is simply specified as the distance light has traveled [math]w_c[/math]. You just rewrite the equation as: [math]s^2 = \Delta\,r^2 - \Delta\,w_c^2[/math] Instead of negative time, you'd get negative spatial displacement in four-dimensional space.

Sorry Sensei, The solution to this challenge had nothing to do with programming.

Again, thank you Mordred! I really do appreciate it

Thank you Mordred and Studiot! I really do appreciate the help, and I will study the material and begin researching those topics as soon as I can. Swansont, I'm not sure if any answer that I reply with will be satisfactory. Right now I'm at work programming a new module for the company. So, I am unable to give a lengthy reply at the moment. Once I get home from work, I will see what I can come up with for a reply.

I appreciate both of you taking the time to familiarize yourselves with my theory of temporal uniformity. I look forward to discussing the theory with both of you and anyone else that wants to join in the conversation. Please note, that I posted my theory when I first joined SFN. Back then I was definitely a green horn when it comes to discussing science and, even though I have extended my knowledge of physics, I still do not have all of the knowledge needed to fully argue all of the finer points needed to construct a full scientific theory. However, I have been working rigorously to remedy my ignorance. With that being said, I am very talented when it comes to mathematics and I love solving mathematical problems and discovering new mathematical relationships (new to me anyway ). The following links are to various posts here at SFN that I have made regarding mathematical relationships that I've discovered: Discoveries by Me - Deadalus and mathematical challenges that I have posted (most of them are my own design): Deadalus' First Challenge Deadalus' Second Challenge Deadalus' Third Challenge Deadalus' Fourth Challenge Deadalus' Fifth Challenge Deadalus' Sixth Challenge Deadalus' Seventh Challenge Deadalus' Eighth Challenge Deadalus' Ninth Challenge Deadalus' Tenth Challenge Deadalus' Eleventh Challenge I mention this because as you review the entire thread, you will notice that I have matured in my ability to make a valid argument. However, the mathematical models that I have proposed within this thread are flawed, and I fully realize this. I'm still teaching myself Tensor Calculus so that I can properly apply my theory and incorporate general relativity. As you have no doubt noticed, most of the mathematics presented thus far are based solely on special relativity. So, you could state that what I have constructed is actually a special theory of temporal uniformity. Of course, I have no problem collaborating with others that can help me incorporate general relativity into temporal uniformity, but I have no problem attempting this on my own. After all, learning new mathematics and physical concepts is the fun part. Plus, I love making mathematical models whether they are accurate or not. It's still good practice. With that in mind, I look forward to debating temporal uniformity and I hope that I can continue to refine and mold my theory into an actual scientific theory that can be considered to have merit. Of course, the only way I can do this is by exposing what I have thus far and debating the concept with my peers. Again, thank you for taking interest in my work.

This idea of yours that attempts to measure natural processes vs. intelligent processes based on how many solutions are available is logically flawed. So, if being hungry is a natural process and you consume food as a solution to this, you are assuming that consuming food is the only solution available and hence it must be a natural process. Then, to determine if it's an intelligent process, you are stating that it will have more than one solution. So, if I bring my manager two or more paperclips and a stapler, then I have put some thought into the process and have arrived at multiple solutions to my managers problem. So, what about planetary formations? There are a billion different way ways that matter can come together to form the planets as they exist today. According to you, this results in planetary formation as being an intelligent process, but clearly it's a natural one. See what I mean? Just because something has multiple solution doesn't indicate that it's a natural process vs. an intelligent one. There is nothing Nobel Prize worthy in your statements at all. It's not even interesting. If you were to demonstrate how entropy could be used to determine natural processes vs. intelligent ones, then you might have something. For instance, natural processes usually always increases the entropy of a system or collection of particles because it takes more energy to reorganize a collection or particles than it does to cause them to be disorganized. However, intelligent beings usually take disorganized collections of particles such as metal ores and such, and organize them into cars, tools, and even paperclips. So, intelligent processes could arguably reduce the entropy of a system or collection or particles while natural processes increase the entropy of a system or collection of particles. However, even these statements about entropy aren't always true, but at least it would've made a more interesting argument than stating intelligent processes are those that have multiple solutions to the problems at hand and natural processes only have one solution. Such an argument is horribly flawed from the start. Please, don't...

There has been a lot of talk about the nature of time in the forums here lately. So, I'm going to try and answer these questions here in my thread on temporal uniformity. Before I can do this, I think it's important to bring everyone up to speed on how time is defined within the framework of temporal uniformity. I'm going to start from the beginning and make a series of falsifiable statements that I believe encompass the very nature of time itself. However, I have to apologize up front for such a long post, but it's necessary to introduce simple building blocks and go from there. What is Time? In order to understand the nature of time, we need to understand what it does and how it behaves. This requires making valid observations about time and its properties, and then construct a definition for time that encompasses these observations. So, let's list all of the observations we can make about time that we know are true. We experience the passage of time as a duration, which is relative to the observer's frame of reference. Therefore, time is observed to speed up or slow down relative to various frames of reference. Although the passage of time is relative to an observer, the passage of time is continuous. e.g. we don't observe objects disappearing and reappearing at different points in time because their clocks speed up or slow down. We observe a clear direction through time such that we exist in the present moving towards the future leaving the past behind. Although we experience a direction through time, we cannot see the dimension of time. When plotting the path matter and energy takes through space, an extra variable is required to order events such as changes in position. In physics, we define this extra variable as time and we use clocks to measure it. Because it is mathematically impossible for anything to move the space with an infinite speed, the act of changing position through space requires a duration of time. This is what it all boils down to in the end. This entire post is meant to emphasize this observation which demonstrates that time is a mathematical consequence of traversing distances through space at finite speeds. This will be the theme for my arguments regarding the nature of time. I really can't think of anything else that we can say about time that is an actual observation, but there are a few preconceptions that we can list that fall right in line with surreptitious57's questions. These preconceptions usually revolve around time travel; the idea of being able to physically move through space-time in such a way that allows matter and energy to travel to the past. Time might exist physically as a temporal dimension where matter and energy continues to exists along this dimension arranged the way it was in the past and will be arranged in the future. Time might exist as some physical dimension that everything moves through, but only in one direction such that we could travel to the past if we could reverse our direction through time. Time might exist according to the many worlds interpretation of quantum mechanics and there could be an infinitude of parallel universes that are defined by every possible event that can happen. If time travel is possible, then temporal paradoxes are possible, and you could go back in time and kill your grandfather before your father was born. The paradox that I find most interesting is the one Michio Kaku mentioned about traveling to the past and killing yourself right before you time traveled. Temporal Uniformity attempts to explain our observations of time and reconcile our preconceptions using a consistent mathematical definition for what time actually is. In doing so, we can explain all of our observations of time while demonstrating that time travel, as understood as the act of traveling to the past and interacting with matter and energy as it was arranged back then, is impossible. This frees us from temporal paradoxes, defines parallel universes which allow dark matter, dark energy, and dark flow to exist, and provides us with answers to some of surreptitious57's questions. We'll begin by discussing space and energy. Space and Energy In temporal uniformity, space is defined as a collection of points where each point is separated by some distance from each other and are organized along dimensions. Basically, it's just a metric space that is occupied by energy in all of its various forms. As will be demonstrated, there is no need to introduce some temporal dimension. However, we still need a way to order events, but we don't need time in order to do so. After all, there are really only two things the make up the universe; space and the various forms of energy that occupies it. I think most people have this misconception that there exists some fabric of space that can expand or shrink. I could be wrong, but it seems more likely that what we perceive as expanding or contracting space is actually the result of how various fields that are generated by matter and energy affect the motion of matter and energy that traverses such fields. Furthermore, things like "quantum foam that is theorized to be the 'fabric' of the Universe, but cannot be observed yet because it is too small" and virtual particles that pop in and out of existence are the result of how energy behaves at different points in space and at different scales. If we existed as charged particles moving through a magnetic field, then the space around us would be defined by the shape of the magnetic field, which is definitely non-Euclidean. Of course, gravitational fields are very different than magnetic fields. However, both fields are generated by the energy contained within matter and both fields affect how energy moves through space. The important thing about these fields is that they change the metric of space for the energy that exists in it, which in turn affects how energy moves through it. Regardless if space actually bends or not, once you define a metric space and introduce energy, there is only one thing that is physically possible; energy can now change position through space. After all, the only thing energy can do with respect to space is change position through it. Granted, energy can interact with itself and other forms of energy in several different ways, but it can only do so if it is allowed to change position through space and come into contact with other forms of energy in the environment. If energy could not change position through space, then no interactions could take place, and the universe would be forever static. Light wouldn't be able to traverse the vast distances between galaxies, and it would be impossible to perceive the universe because electrical signals in our brains wouldn't be able to traverse the neural pathways. The universe as we experience it can only exist when energy is allowed to change position. Now, I need to introduce a point of clarity here for the sake of our experts, moderators, and everyone else. There has been much debate regarding motion when it comes to quantum mechanics (QM) where motion is not as easily defined. Most people assume that motion is simply the act of a solid body changing position through space such as a baseball. However, subatomic particles such as electrons do not behave as if they were tiny baseballs orbiting a tightly packed nucleus of protons and neutrons that are also like tiny sized baseballs. So, this idea of motion simply doesn't suffice to explain what is observed. In order to resolve this discrepancy, we are forced to define motion simply as the act of energy changing position through space. After all, doesn't this encompass the very essence of what is observed at any scale? For example, when we look at standing waves or just waves in general, we see motion. However, it is not the same type of motion exhibited by a baseball. Figure 1 - Wave motion. Are the particles of the wave moving up and down creating the appearance that the wave is moving to the right, or are the particles actually moving to the right? How can we define the position of the wave? It's not like we can define a center point that allows us to track how the wave changes position like the baseball. Regardless of how complicated the motion is, we still know that the structure of the wave is in motion and its energy is changing position through space. So far, we have defined the universe as being comprised of only two things; space and the energy that occupies it. Time has not been included in our definition for space because, as it will be shown later, it exists as a property of space and not as a separate phenomenon. We will define what time is but, for or now, let's recap the finer points discussed thus far. The universe only consists of space that is occupied by energy in its many forms. Motion is defined as the act of energy changing position through space. If you agree with these statements, then the discussion can move forward. Now that we have defined space and energy, we need to discuss how we measure and quantify it. Measurements Whenever we take measurements, we can only do so by exploiting an attribute inherent to whatever it is we are measuring. For instance, space is composed of points that can be organized along spatial dimensions where each point is separated by some distance. One of the defining attributes inherent to space is distance separating the points within it. Without distance separating the points, there wouldn't be any space. So, the only way we can directly or explicitly measure distance through space is by using a predefined unit of distance. The unknown distance through space is quantified in multiples of this predefined unit of distance. Direction through space is also quantified using predefined units of distance along the dimensions of space defined by a coordinate system. Therefore, distance is an attribute that defines what space is and we can only directly measure space using a unit of distance. Just look at how we measure length, direction, areas, and volumes. All of these things that define what space is, are the result of measurements of distance. The same is true for anything else we measure. We are forced to use mass to measure mass. Given a balance / scale and several unit masses, we can measure the unknown mass of some object. If we are measuring probabilities, then we are forced to take measurements of the number of times something happened in a particular way. No matter what it is we are measuring, we always have to use the thing we are measuring to take the measurement. Otherwise, it would be impossible to measure. The fact of this statement can be seen in our basic units of measurement such as feet, meters, grams, kilograms, etc... Each one defines a predefined unit of the thing we are measuring. Now, you might argue that you can use measurements of time and speed to derive the value for the measurement of distance an object has traversed. However, such a value is implicit because it relies on measurements that are directly / explicitly taken of other physical phenomena that are plugged into an equation provided by a theory of ones choosing that defines how one or more of these explicit measurements relate to the value of the unknown quantity. The derived value of the measurement was not directly observed and relies on the accuracy and precision of the theory that defines such relationship. This provides further evidence that we can only use the physical phenomena itself to explicitly measure it. Let's recap. In order to explicitly take a measurement of physical phenomena, you have to use the phenomena itself to take the measurement. Values derived for measurements using equations defined by physical theories are implicit because the measurements were not directly observed and rely on the correctness of the theories that provided the equations. Since we are forced to use the phenomena itself in order to measure it, we simply have to ask ourselves how we measure time. Understanding the mechanics that drives our measurements of time should reveal the very nature of time itself. Such an understanding should resolve temporal paradoxes, define the driving mechanism for change, describe relativistic affects such as time dilation, and explain the arrow of time. Measuring Time with Motion Why is it important to define and understand how we take measurements? How can we even begin to answer questions about time if we don't even understand the underlying nature inherent to time itself? It all comes back to the statement that In order to measure any physical phenomena, we are forced to use an attribute inherent to the phenomena itself. When we examine how we measure time, we find that we always use motion to take the measurement. A sun dial works because the Earth rotates, grandfather clocks works due to the swing of their pendulum, spring watches use a spring to turn gears, digital watches use electricity to cause crystals to oscillate, light clocks reflects photons between two plates, and atomic clocks measure quantum mechanical properties derived from the motion of the energy contained within atoms (I will address atomic clocks later in this post). The mechanism that measures time in all of these devices does so by some form of energy changing position through space. If we can agree that we use motion as defined by energy changing position through space to measure time, then motion must be inherent to time. If motion is inherent to time, then time is purely spatial and is governed by distance, which makes sense because the only thing that exists in the universe is energy and space. Because it is mathematically impossible for energy to traverse distances through space with an infinite speed, the passage of time must occur. So, our experience of the passage of time is a mathematical consequence of motion being restricted to finite speeds and nothing more. This is no different than how objects seem smaller at greater distances. Such things are mathematical consequences of distance. Therefore, in temporal uniformity, time is defined as a mathematical consequence of energy changing position through space with finite speeds. However, we measure motion as a change in space over a change in time. How can time be a consequence of motion if our definition for motion is based on units of distance and time? This contradiction can be resolved by analyzing how we use motion to measure motion. Because energy has to change position through space for change in the environment to occur, when we use a clock to measure the rate of change of a physical property, we are actually using the motion of the mechanism in the clock to measure the motion of the energy causing the physical property to change. In essence, we are using motion to measure motion no different than how we use distance to measure distance. Besides, a change in position [math]\Delta\,x[/math] does not require measurements of time. The change in position is purely a spatial property which relates back to measuring distances. We introduced the concept of measuring time because energy can change position at different rates. However, we don't need measurements of time to measure these different rates at which energy can change position through space. All we need are measurements of the distance traversed for some unit of motion compared to the distance traversed by some form of energy. If this is true, then we should be able to remove the time variable [math]t[/math] from every equation in physics, and replace it with a measurement of distance. We can demonstrate this concept using a light clock. Figure 2 - The light clock to the left is at rest and the clock to the right is moving relative to the observer's coordinate system. The light clock to the left is stationary in the coordinate system or frame of reference (FoR) of the observer, and the clock to the right is in motion relative to the observer's FoR. For now, let's examine the light clock to the left that is stationary. There are only two ways to use the clock. We can either count the number of times photons have traversed the distance between the two reflective plates and define that measurement as a unit of time, or we can measure the distance the photons traversed between the plates. Both measurements are equally valid and allows us to quantify motion and order events. [math]t = d_c[/math] where [math]t[/math] equals a unit of time and [math]d_c[/math] is the distance traversed by the clock mechanism. Therefore, a unit of time is nothing more than a normalization of a unit of distance. If we choose to use measurements of distance, then we can define speed as the change in distance traversed by energy divided by the change in distance traversed by the clock mechanism. [math]\text{speed} = \frac{\Delta\,d_e}{\Delta\,t} \ \ \text{or} \ \ \frac{\Delta\,d_e}{\Delta\,d_c}[/math] where [math]\Delta\,d_e[/math] is the change in distance traversed by energy when the change in distance traversed by the clock mechanism equals [math]\Delta\,d_c[/math]. If the speed is constant, we could multiply the total distance our clock mechanism has traversed by our newly defined speed, and we can derive the distance the energy traversed through space without having to use units of time. [math]d = \frac{\Delta\,d_e}{\Delta\,d_c} \times d_c[/math] where [math]d[/math] is the calculated distance. Again, this is no different than measuring distance with a ruler. We are simply quantifying the distance traversed by energy in multiples of the unit distance traversed by the clock mechanism. So instead of measuring motion in units of distance per units of time, we are comparing distance to distance, which adheres to the rule that we have to use the phenomena itself to take measurements. The standard equation for motion using only measurements of distance is defined no differently than when we use values of time. So, we can completely rewrite every equation in physics that uses measurements of time to use measurements of distance instead. [math]d = \frac{1}{2} \left(\frac{\Delta\,d_e}{\Delta\,t^2}\right) t^2+\left(\frac{\Delta\,d_e}{\Delta\,t}\right) t + d_0[/math] [math]d = \frac{1}{2} \left(\frac{\Delta\,d_e}{\Delta\,d_c^2}\right) d_c^2+\left(\frac{\Delta\,d_e}{\Delta\,d_c}\right) d_c + d_0[/math] As a result, measurements of time are the only units in physics that can be replaced by units of distance. Such a contradiction is a violation of dimensional analysis, which provides further evidence that when we use time to measure rates of change in physical properties, we are actually using motion to measure the motion of energy changing position. Again, let's recap. There are only two measurements a clock can make; a measure of the number of times the clock mechanism has completed a cycle, or the distance the clock mechanism traversed throughout the cycle. What we experience as the passage of time is the mathematical result of energy being restricted to finite speeds. Since it is mathematically impossible for energy to traverse space with an infinite speed, the passage of time must occur. For any equation in physics, we can replace the time variable [math]t[/math] using measurements of distance. Units of time become normalizations for units of distance and are interchangeable. Although we can demonstrate that we use motion to measure time, there exists a different view regarding time that is based on change. That it is change that drives the mechanism of time. So, let's now discuss how change is propagated throughout space. Change in a System Newton said it best in his laws for motion. For every action there is an equal and opposite reaction, and an object will maintain a constant velocity unless acted upon by an outside force. Although these statements apply to the classical world of physics, they also apply to the QM world as well when we consider that the only thing energy can do within space is change position. If energy was not allowed to change position, then how could it interact with other energy in the environment? How could the window break if the ball did not change position through space, and how could we observe the ball breaking the window if the energy of the light emitted from these object is also not allowed to change position through space? The only observation we can make is that change in a system can only occur when energy is allowed to change position through space and interact with other energy in the environment. Thus, the very definition of interaction is energy changing position. Because energy can change position through space, an organized collection of particles will become disorganized if the particles are allowed to move around freely. However, although physics allows it, we never see the disorganized particles reverse their motions and reorganize. So, we observe what we call the arrow of time. However, entropy and the arrow of time can be explained by energy changing position. Let's take our collection of particles and place them at the origin point of a coordinate system. Each particle in the collection has a defined position in that coordinate system, and the amount of disorder in the collection increases as the particles move farther away from their original positions. So, we could define the measure of entropy for the collection of particles as the total sum of each particles change in distance from its original position in the collection. If all the particles were at their original position, then measure of entropy would be zero. As entropy increases, the particles move farther away from their original position. However, this doesn't explain the arrow of time. To understand why smoke doesn't go back into the cigarette or why an ice berg doesn't jump out of the water and reform the glacier, we only have to examine the physics of a single particle. In order to set the particle in motion, we have to apply some amount of energy [math]E_1[/math] to it. Now that the particle is changing position, the disorder or entropy of the collection of particles is increasing. To stop entropy from increasing, we have to apply the same amount of energy [math]E_1[/math] to bring the particle to rest. However, the entropy of the collection of particles is still higher than it was before we applied energy to the particle. In order to reverse entropy and restore the collection of particles to its original form, we have to apply some energy [math]E_2[/math] to the particle to reverse its motion. Then, we have to apply the same amount of energy [math]E_2[/math] to bring the particle to rest at its original location restoring the collection of particles to their original state. Therefore, it takes more energy to restore the collection of particles to their original state than it does to increase its entropy. The amount of energy needed to set a single particle in motion and increase the entropy of the collection of particles is [math]\text{increase entropy} \rightarrow E_1[/math] The amount of energy needed to reverse the motion of the particle and lower the entropy of the collection of particles is [math]\text{reverse entropy} \rightarrow E_1 + 2 E_2[/math] Because the amount of energy needed to increase the entropy of a system is less than the amount of energy needed to restore the system to its original state, the collection of particles will continue to become disordered and the arrow of time is observed. So, although physics allows for these particles to reorganize themselves, it takes more energy to restore a collection of particles to their original form than it does to cause them to become disordered. This is why the arrow of time seems to move in only one direction, Entropy and the arrow of time are caused by energy changing position through space. It takes more energy to organize a collection of particles than it does to cause them to be disordered. The only thing various forms of energy can do as a result of interacting with other forms of energy or itself is to change position through space such that change in the environment can only occur when energy is allowed to change position through space. So, even entropy and the arrow of time can be explained by energy changing position, but we still need to consider atomic clocks. After all, they are based on QM where the motion of energy is not so easily defined. QM and Motion I believe the biggest confusion regarding QM for most people is what we are actually measuring when we apply energy to a quantum mechanical system. Because we cannot physically see these subatomic particles such as electrons, we cannot directly measure how energy within the system is changing position. Instead, we attempt to detect their position in space by using some form of energy to interact with these particles or fields. Then, we determine the position where they occurred along with how many times we were able to detect the particle at that position. This allows us to build a probability space of where the particle occurs and the probability that you will find it at any given position in that space. The following image demonstrates these atomic orbitals, which "can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus." Figure 3 - False-color density images of some hydrogen-like atomic orbitals (f orbitals and higher are not shown). (Wikipedia atomic orbitals) Measurements in QM such as those taken for quantum numbers or quantum fields are completely different than measuring how the energy contained within these particles or fields is changing position through space as defined in the classical sense. QM deals with aspects of energy that can't be explained using classical mechanics. However, QM behaviors occur within space and must be caused by energy changing position and interacting with energy in the QM system / environment. As defined earlier, the only thing energy can do within space is change position. Granted, energy takes on many forms where each form has special properties that cause different forces to be generated that in turn affect the motion of energy in the QM system but, despite the cause that set it in motion, the only thing energy can do as far as space is concerned is move through it, which allows energy to interact with the environment. Even if we never learn how energy within these particles or waves is changing position through space, how could change in an atom or particle occur if energy wasn't allowed to change position and interact with other energy within the system? Just because we don't know or can explain how this energy changes position doesn't mean that motion does not occur within QM systems. Furthermore, force is propagated in QM through force carriers. If the energy contained within these particles was not allowed to change position through space, then the universe would not be able to exist much less use them to take measurements of QM systems. An argument was made that we cool the atoms in atomic clocks to near absolute zero as to eliminate motion from the QM system, and yes this is somewhat true. However, it is not an honest argument. We don't super cool the atoms to eliminate the motion of the energy in the atoms. We super cool the atoms to eliminate the motions of any energy within the environment that would interfere with the motion of the energy contained in our atoms. Then, when we use energy to interact with these atoms to create atomic clocks, we can measure the QM affects that result from the energy changing position within the atoms themselves. We may never know how the energy within atoms is actually changing position through space in a classical sense but, because energy has to change position through space to interact with other energy in the system, we observe QM properties that are a result of such motions. Our entire existence occurs because energy changes position through space. Measurements of quantum numbers, fields, and other QM effects are not the same as measurements of energy changing position through space. QM effects arise when energy changes position through space. Energy contained within atomic clocks must change position through space for the clock to work. Because we can't measure how energy in atomic clocks change position through space, we have to count the number of times some quantum number completes a cycle. I realize that my argument for QM might be considered weak. However, if we agree that the universe is comprised of space and the energy that occupies it, then the only way change can propagate is by energy changing position through space, which includes QM systems. I would also like to add that even though quantum teleportation seems to allow information to traverse distances through space instantaneously, energy must still be allowed to change position through space for it to work. I figured this additional statement was required to make because I can see someone arguing this point. Temporal Uniformity So far, we have explained a few of our observations of time: We experience the passage of time as a duration, which is relative to the observer's frame of reference. The passage of time occurs because energy cannot move through space with an infinite speed. We observe a clear direction through time such that we exist in the present moving towards the future leaving the past behind. It takes more energy to restore a collection of particles to their original arrangement than it does to cause them to become disordered. When plotting the path matter and energy takes through space, an extra variable is required to order events such as changes in position. Instead of measurements of time, we can now use measurements of distance when plotting that path energy takes through space and to order events. We still need to explain why time can speed up or slow down, why we don't see a dimension of time, and how we can resolve temporal paradoxes by removing the temporal dimension of time altogether. In order to do this, we have to discuss how four spatial dimensions can be used to describe how we experience time including relativistic affects such as time dilation and length contraction. Temporal uniformity states that the universe consists of four dimensions of space where the energy contained within this space is moving away from a single point at the speed of light where the big bang event occurred. Once the energy from the big bang cooled enough to form matter, this matter became trapped in a manifold of space defined by the boundary of a 3-sphere or four-dimensional sphere that is radially expanding at the speed of light. The reason why matter and energy is bound to a 3-sphere is because the energy that formed this matter started its journey moving away from a four-dimensional point in space at the speed of light where the big bang event occurred. Because matter and energy is moving at the speed of light along a radial vector of a 3-sphere, we can only observe light that moves in the three remaining dimensions that are perpendicular to these radial vectors. So, this three-dimensional boundary of this four-dimensional sphere becomes the space that we and everything that is observable exists; essentially our view of the universe. Figure 4 illustrates a two-dimensional cross-section of a four-dimensional sphere with the observer [math]O_b[/math] located at the coordinate where the big bang event occurred and the observers [math]O_n[/math] and [math]O_r[/math] located on a boundary defined by the four-dimensional sphere. Figure 4 - A two-dimensional cross-section of a 3-sphere with three observers defined at various locations. This view of space and the energy that occupies it gives us a natural explanation for why we observe the space in between galaxies expanding. It also explains why space is expanding everywhere with no observable center to the expansion. We simply can't see the center to this expansion because it exists in four-dimensional space. However, it's not space or time that is moving or expanding. Instead, it's the energy radiating away from a four-dimensional point at the speed of light that is causing the observers [math]O_r[/math] and [math]O_n[/math] to move away from each other with a velocity [math]V_r[/math]. Although this provides us with an explanation for how space can expand, it doesn't explain the acceleration that is observed, or provide us with an explanation for gravity. However, the affect of the expansion for this 3-sphere is numerically identical to the "bug on a band" problem. The following is from a post I made in the thread, "Is Krauss looking at this right?". "Two views of an isometric embedding of part of the visible universe over most of its history, showing how a light ray (red line) can travel an effective distance of 28 billion light years (orange line) in just 13 billion years of cosmological time. Click the images to zoom. (Wikipedia)" The point I was making in the quote is that if space is the rope and it stretches in accordance with the ΛCDM scale factor and we think of the ant's speed as the speed of light, then this analogy is numerically accurate to the observed expansion of space. Therefore, the concept that we are bound to a 3-sphere that is expanding at the speed of light through four-dimensional space fits within our current framework of physics. So, in order to explain dark matter, dark energy, and dark flow we have to expand upon the idea of being bound to a 3-sphere in four-dimensional space, which we will do later in the section on Space, Gravity, and Time Dilation. The reason why it is important to introduce this into the discussion is because it provides us with a mechanism that explains why we can't perceive four-dimensional space directly and allows us to explain gravity and gravitational time dilation. As explained above, since we are bound to a 3-sphere that is expanding radially at the speed of light, we can only see light that moves along dimensions of space that are perpendicular to radial vectors that comprise the 3-sphere. Thus, we cannot physically see this four-dimensional space, and can only observe how it affects energy as it moves through it. Furthermore, if we consider that the energy of the big bang event didn't radiate away from this four-dimensional origin point all at once, there would exist layers of 3-spheres each expanding radially at the speed of light that contain their own matter and energy. Each layer would be a separate universe altogether, but each layer would still exist in the same four-dimensional space and potentially interact with each other through gravitational fields. Because each layer has a radial velocity that is zero relative to the radial velocity of other layers, matter and energy within these other layers could still affect each other gravitationally. However, because each layer has a radial velocity equal to the speed of light relative to the four-dimensional point in space where the big bang event occurred, the gravitational affects of each layer could only affect matter and energy along dimensions that are perpendicular to radial vectors that comprise the 3-spheres. Because matter and energy within layers along the outermost edge of the expansion of the big bang are moving away from each other with a greater velocity [math]V_r[/math] than the inner layers, these outer layers would pull the matter and energy within the inner layers along with it. This not only explains dark matter, but also provides a mechanism for dark energy, which would also be observed as dark flow. Figure 5 illustrates these layers as three-dimensional spheres. Figure 5 - A three-dimensional representation of the universe demonstrating various layers defined by the surface of the spheres that contain individual local views of space. Figure 6 illustrates how these 3-spheres are comprised of matter and energy, and how dark matter and dark energy can be represented as different 3-sphere layers. Figure 6 - A two-dimensional cross-section of four-dimensional space showing how dark matter existing at different layers or 3-spheres can give rise to dark energy and dark flow. Some of you might disagree with this view space and time because we are taught that anything with mass cannot move at the speed of light. However, when we use special relativity to derive our four-velocity through space-time for an object at rest, we find that the magnitude of this four-velocity is equal to the speed of light. Now that we have defined space as being four-dimensional, and that matter and energy moves through this space at the speed of light restricted to the boundary of 3-spheres, we can explain why time dilates. This has nothing to do with some actual physical dimension of time. Instead, it relates back to how energy can only traverse distances through space at finite speeds. If the metric of space changes how distances are traversed, then naturally clocks will measure time differently based on an observer's FoR. Space, Gravity, and Time Dilation If we consider that time is just a property of space that is a consequence of energy moving with finite speeds, then it becomes easy to explain time dilation. Figure 7 - The light clock to the left is at rest and the clock to the right is moving relative to the observer's coordinate system (figure 2 revisited). If we examine the light clock on the right that is in motion relative to the observer's FoR, we will notice that the path the photons have to traverse between the two plates has been elongated. Because the speed of light is the same for all observers, the observer at rest relative to the clock in motion will notice that the clock ticks more slowly. The tick of the clock doesn't change because it moves through time slower than the observer. The tick of the clock changed because the metric of space has changed causing distances to be affected. The path that the photons have to traverse has been elongated, which affects how the energy of the photons changes position through space. It's as simple as that. There is no special temporal dimension where the clock is moving slower than the observer. In order to understand gravity, we have to understand that what we observe in the universe is actually a three-dimensional projection of matter within four-dimensional space. Because energy is moving away from a four-dimensional point in space at the speed of light in all directions (where the big bang event occurred), we lose the ability to perceive light along our local radial vector of space. So, if the universe was three-dimensional, and we were bound to the surface of a three-dimensional sphere that was radially expanding at the speed of light, we would only perceive the universe as having two-dimensions as defined by the surface of the sphere. However, the universe would still consist of three dimensions of space. As previously discussed, when we apply this concept to four-dimensional space, we end up with three observable dimensions of space. Now, as objects gain mass they slow down as a result of conservation of momentum. This is also applies to motion through four-dimensional space. However, objects that gain mass don't seem to slow down along the radial vector of expansion and fall outside of the boundary defined by the 3-sphere and completely disappear from our local view of the universe. You can think of this no different than cars moving down the highway at different speeds. Eventually, cars that are moving slower down the highway will disappear from the view of cars moving faster. So, we are forced to expand upon the concept of being bound to a 3-sphere that is expanding radially at the speed of light because just defining a boundary that arises as a consequence of the speed of light isn't enough to explain how conservation of momentum plays its part and why objects with mass simply don't vanish from this boundary. To explain why matter and energy remains bound to these 3-spheres, we have to speculate that these layers that were formed by matter and energy moving away from a four-dimensional point in space at the speed of light where the big bang event occurred is more than just a result of speed. Instead, if we consider that most of the energy from the big bang event is in the form of gravitational waves, then we can consider that this boundary defined by 3-spheres are actually gravitational waves that formed when the big bang event occurred. Therefore, not only do these 3-spheres arise from matter and energy moving at the speed of light away from a four-dimensional point in space, but that most of the energy contained within these layers is in the form of four-dimensional, spherical, gravitational waves. If we can consider this speculation, then we can explain why objects with mass don't disappear from our own boundary defined by the 3-sphere, and we arrive at a natural explanation for gravity and gravitational time dilation. First of all, due to the law of the conservation of momentum, as objects gain or lose mass its speed will change along all dimensions of space. This includes the higher four-dimensional space that, as explained previously, we can't physically see. However, if these layers defined by the 3-spheres are also gravitational then, as objects gain mass or energy, they will attempt to slow down along their local radial vector. However, instead of completely moving outside of the boundary defined by the 3-sphere, they can only move so far until this extra mass / energy is countered by the gravitational field that is defined by the 3-sphere itself. As the objects gain mass, they can only move so far until the field counters this motion and continues to carry this matter and energy along with the expansion. So, instead of a smooth boundary as defined by the 3-sphere, it's more like the surface of a golf ball where the dimples represent the displacement of objects with mass relative to the smooth boundary of the 3-sphere itself. Figure 8 - Gravity as demonstrated from a two-dimensional space that exists in a three-dimensional universe. As figure 8 illustrates, if we existed on the two-dimensional surface of a three-dimensional sphere that is expanding radially at the speed of light, then objects with mass would create an impression in the higher three-dimensional space the comprises the universe. This causes an elongation of distances when observed from the higher, three-dimensional space as can be seen in figure 8. However, we cannot observe this higher dimension of space because we are moving at the speed of light along our radial vector from the center of the sphere to the point we are located. The means that we can only see light that is perpendicular to this radial vector. Although the true distance through the higher dimension of space is the length of the green curve from the points C to D, we'd only perceive the distance through space as the orange line from the points A to B. To us, it would appear flat. This distortion of distance in higher dimensional space, is why gravity and gravitational time dilation exists. As an observer moves along the green path starting from point C moving towards the massive object in between C and D, for every unit of distance the observer traverses in the two-dimensional space, the distance traversed in the higher three-dimensional space increases. Although we can't see this higher dimension of space, the observer would still be traversing greater and greater distances for each unit of distance traveled in the two-dimensional space. This is why the observer experiences the force of gravity. The distance in the higher dimension of space is actually increasing for each unit of distance traversed within the two-dimensional manifold, and it is this effect that causes clocks to tick more slowly in gravitational fields. No different than distances being elongated for the light clock that is in motion relative to the observer, the distances as observed in the higher dimensional space is being elongated by the gravitational field and causing the clock to tick more slowly. Again, none of this has to do with the existence of some physical dimension of time that we call the temporal dimension. Instead, time dilation, gravity, and gravitational time dilation can all be explained by changes in the metric of space that causes distance to contract or expand, which in turn affects the distance the mechanism in the clock has to traverse in order to measure time. It's as simple as that, and we don't have to invoke some temporal dimension to measure time and order events. The Nature of Time When we apply this concept to four-dimensional space, we can explain why we perceive the universe as having three spatial dimensions while experiencing time. However, we do not need to invoke some physical temporal dimension where energy exists as it was in the past or as it will in the future. When we consider that time is a mathematical consequence of energy traversing distances through space at finite speeds, then the only way one can "time travel" is to physically arrange all of the matter and energy to the way it was in the past or how it will be arranged in the future, which is physically impossible. When our equations, such as those in general relativity, give us a negative change in our time variable [math]t[/math], we don't have to interpret this as a way to travel back in time. The view as provided by temporal uniformity suggest that instead of traversing some temporal dimension, that we are really traversing the higher, four-dimensional space that comprises the the universe such that we end up at a point in four-dimensional space outside of the boundary as defined by the four-dimensional sphere or 3-sphere that comprises our local three-dimensional view of the universe. In the case of wormholes, we'd just end up in a different three-dimensional space defined by a completely different 3-sphere. The matter and energy located in our manifold of space would still be expanding outward with the rest of the layers and you'd simply end up in a different layer. So, using the framework of temporal uniformity, we can now answer some of surreptitious57's questions. Time is a mathematical consequence of matter and energy being restricted to changing position through space at finite speeds. It's simply impossible for anything to traverse space with an infinite speed, which is required in order to change position without any duration of time to be experienced. We perceive the universe because electrical signals in our brains traverse the distances that separate our neurons. If these electrical signals could traverse the neural pathways with infinite speed, then our brains could process every single piece of information received from the environment and we could have every single thought instantaneously. If the electrical signals in our brains traversed the distances along our neural pathways with infinite speed, then they could traverse these pathways an infinite number of times before any amount of time would pass. The result of this would be as though time stopped. So, at least within temporal uniformity, time is not a dimension at all and, as demonstrated earlier, we don't even need measurements of time in order to formulate the laws of physics or order events. Because points in space exist regardless if time is defined or not, the energy that occupies space can change position within it. The result is the occurrence of motion, and it is the motion of energy through space that causes change in the environment to occur. Therefore, matter and energy can only move through space because time does not exist as a physical dimension all by itself or even as a part of space. Time is nothing more than a mathematical consequence of distance. As explained in the section, Change in a System, the arrow of time occurs because it takes more energy to restore a collection of particles to a particular arrangement than it does to cause the collection of particles to become disordered. The amount of energy required for entropy to increase is [math]\text{increase entropy} \rightarrow E_1[/math] where the amount of energy required to reverse entropy is [math]\text{decrease entropy} \rightarrow E_1 + 2 E_2[/math] In the section, Temporal Uniformity, we demonstrate how space can expand naturally without having to invoke some fabric of space that is expanding itself. The effect is best illustrated in the following image. Although we didn't discuss black holes, we did define how gravitational fields affect the metric of space causing distances to expand or contract. If distances become elongated, then the mechanism inside a clock that uses motion to measure time will tick more slowly. Time dilation occurs because the metric of space changes how distances are defined and, even if we can't perceive this contraction or expansion of space as is the case for gravitational fields, the effect arises because distances are affected. Because relativity theory has shown that the speed of light is the same for all FoRs when measured using the same units, then energy itself and not just clocks is affected by this contraction or expansion of space. So, not only do clocks tick more slowly, but energy itself has to traverse distance for change in the environment to occur. So, observers / people will also age more slowly when placed within gravitational fields relative to observers / people outside of theses fields. However, just because physical processes are affected by the elongation or contraction of distances within or outside gravitational fields doesn't mean that these processes are literally moving slower or faster through time. Sure, people will age differently when observed from varying FoRs, but this effect is purely spatial. That is why my theory is called temporal uniformity. Although we can experience time differently, we still remain temporally uniform as energy changes position through space. In other words, we don't observe object disappearing and reappearing because clocks slow down or speed up. From the FoR of a photon, if such a thing could be said, time could not be measured at all. Take a look at the light clock to the right that is in motion relative to the observer. As the speed of the clock approaches the speed of light relative to the observer, the path that the light has to traverse increases more and more. If the clock was allowed to travel at the speed of light, then the path the photon's have to traverse between the reflective plates becomes stretched to infinity. Therefore, it would be impossible for such a clock to measure time. As for the question, "Has time always existed?", I believe the answer depend on if space has always existed. Although my reply to this is pure speculation, I believe that space and energy has always existed because energy cannot be created or destroyed. So, I believe that space had to exist in order for energy to fill it. If we consider the universe as described by temporal uniformity, not only can we define the big bang resulting in multiple layers of 3-spheres that represent separate three-dimensional universes, but also multiple big bang events that can occur throughout this physical four-dimensional space. So, not only have we defined time within the framework of temporal uniformity beyond the simple definition of that which clocks measure, but we also have derived a definition that encompasses all of our observation of time while demonstrating that our preconceptions regarding time travel are wrong. Sure, there are some speculation on my part, but these speculations fit within our current framework of physics. To demonstrate this I'll will re-post the mathematics I derived that uses the equations of special relativity for time dilation to derive the notion that we traverse four-dimensional space at the speed of light. Thank you for reading this post. I hope that I have clarified, at least within the framework of temporal uniformity, what time actually is. In doing so, we have resolved temporal paradoxes by showing that time travel is impossible, provided explanations for the multi-verse and how dark matter, dark energy, and dark flow exists within our four-dimensional universe, and have defined a consistent definition to explain time.