Everything posted by Daedalus
-
Temporal Uniformity
You are most definitely pardoned Pantheory : ) I made that reference to SR because I have not yet considered gravity except in stating a hypothesis about temporally displaced mass-energy that could explain dark matter and galactic rotation curves. But as you and I have discussed, Temporal Uniformity does have something to say concerning the Big Bang. The next step is to either tackle gravity / GR or attempt to relate Temporal Uniformity to QM. I personally feel that integration with QM is the next logical step because I believe the solution regarding gravity will emerge as a result. However, I do not have illusions of grandeur in that I will achieve this step or that the work I have done thus far will be considered "Nobel Prize" material. But like many of us who pose theories, I do hope that the work I am doing will, in some way, prove to have merit. It is on that note that I would like to extend an invitation to everyone who has the knowledge and is willing to be a part of developing this theory to join in on the fun : ) I would also like to thank AJB, Michel123456, and you Pantheory for all of the support you guys have given me as well as Klaynos and Swansont for debating the topic. I absolutely agree. The main reason which sparked the idea of Temporal Uniformity was due to some of these theories regarding time and QM. My friends and I were watching "The Universe" the Saturday before Easter Sunday. It was the episode that discussed different theories of time. They were talking about the possibility of time travel when I looked over at my friend, Jim, and said "That mechanism for time travel it preposterous!". I don't quite remember which theory they were discussing, but I proceeded to explain to him why I felt that way. The next day, I began developing Temporal Uniformity and have been working on the theory in my spare time ever since.
-
Temporal Uniformity
I appreciate the comment Pantheory. As you can probably tell, I managed to pick up a few things in graphic design while developing class 2 casino gaming devices. To answer your question, Temporal Uniformity by itself is currently just an extension to SR. I am researching QM to see if there is a common ground between my spiraling singularity in comparison to that of ring singularities. I found some interesting material by Don J. Stevens referring to Alexander Burinskii's model which describes electrons as naked ring singularites. Read up on what Don J. Stevens has to say about the electron as a ring singularity: Electron - Ring Singularity Granted, they may be correct or they could be wrong. But, I must consider all sources of information if I am going to find a possible link between the mathematics that I have currently produced with those of QM. To achieve this, I must consider other forces and physical constants within my mathematical model and explore many other theories in Physics.
-
Temporal Uniformity
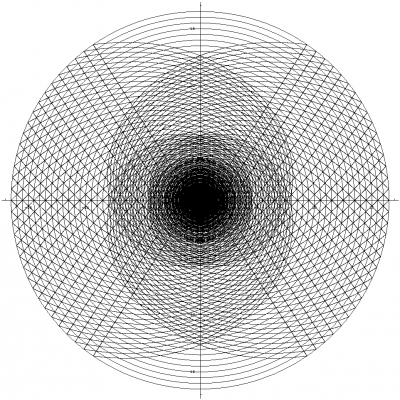
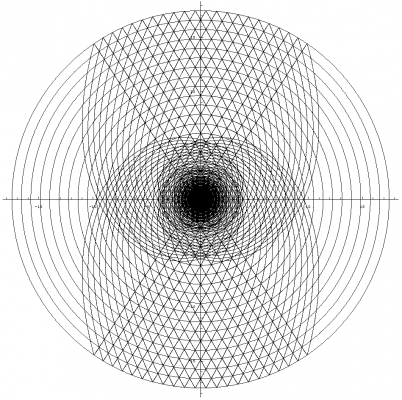
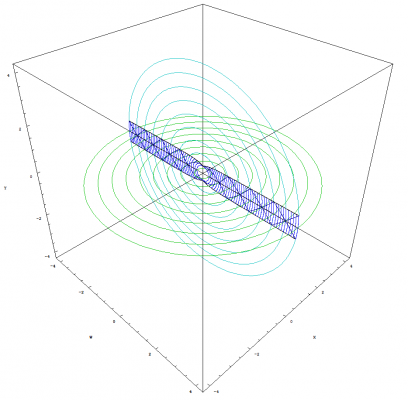
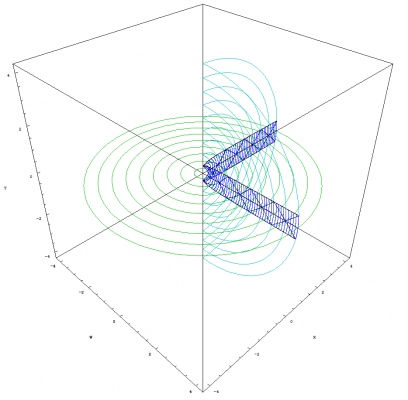
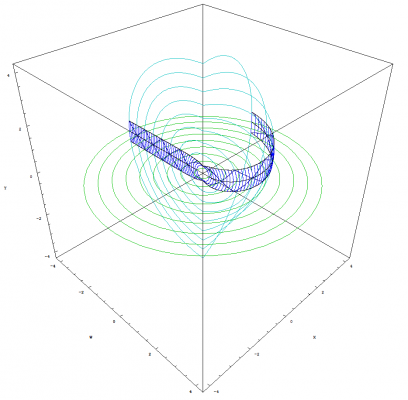
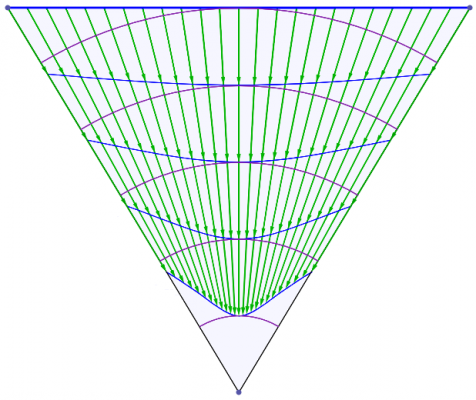
I'm glad you asked Pantheory as these equations and graphs are the result of five months of work. I developed my idea for Temporal Uniformity April 24th, 2011 on Easter Sunday. I opened Photoshop and began to draw the image that I had imagined would explain the phenomena of time and made a hypothesis that dark matter could be temporally displaced matter that caused gravitional effects in our view of the universe. Temporally Uniformity states that regardless of a bodies motion, that body will remain temporally aligned with all other bodies. The graphs from the previous post demonstrates this concept (especially if you look at the image that demonstrates acceleration). The graphs also demonstrate that the space-time vector for all observable bodies, with the tail at the center of the expansion and the head located at the body's current position, is equal in magnitude as demonstrated by graphing two or more clocks. The mathematics and graphs also show that, from our view of the universe, all three observable dimensions of space would appear to be expanding. The image showing one clock that is moving [math]90^\circ[/math] from the other illustrates this concept. A better example of this expanding space would be to plot two clocks that have a smaller angle between them. The image below was created before I had derived any of the equations for the theory. You can see that my equations and graphs fits pretty close to what I was trying to achieve by comparing the above image to the image I have graphed by combining multiple light clocks as seen below. Except, I have only considered the constancy of the speed of light. The above image is soley produced by graphing multiple photon paths, that are radiating outward with the expansion, and by removing the restriction on the parameter, [math]u[/math], so that the path is allowed to continue beyond the boundaries of the reflective plates in the light clock. The rings are reference points as stated previously and can also be thought of as temporally displaced views of the universe. We can also see that the equations produce a spiraling singularity at the center of the expansion. I have rendered detailed graphs of this singularity and we will discuss this topic once we have concluded deriving the time dilation equations. The mathematics also allows for a time before the expansion and, by working backwards from time zero, I produced the following image showing the path of photons flowing inward into the spiraling singularity. I never intended for the mathematics to produce the singularity. My goal was to derive time dilation equations for a path across an expanding sphere so that I could make a post about how we can derive such things for spaces other than flat Euclidean space. You can only imagine my excitement when I was able to produce the mathematics and graphs, based on my original image, that seem to support my ideas. I hope this explanation clarifies as to why I have developed this mathematical model and how it fits within the framework of Temporal Uniformity.
-
Temporal Uniformity
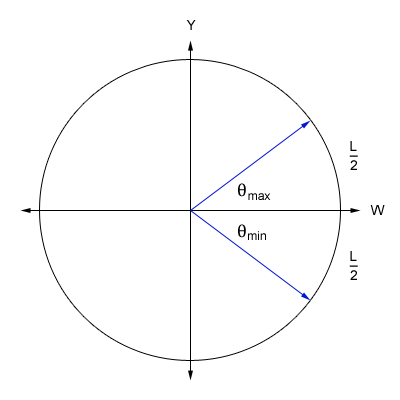
We discussed the equations for describing the angles and path in the previous post, but we really didn't define the path for the photon or parameterize the equations. So we will start by discussing how we will define this path, and the mathematics needed to parameterize the equations. The above image allows us to visualize the problem. We can see that I have positioned the arc of length [math]L[/math] so that it is centered along the horizontal W axis. This bisects the arc into two parts of equal length. We do this so that we can simplify the maximum and minimum angles (shown in blue) that the photon traverses for both, the up and down paths. Using the equation from the previous post that defines the angles, we can calculate the maximum and minimum angles as follows: [math]\theta_{max}=\frac{L/2}{r}=\frac{L}{2\, r}[/math] [math]\theta_{min}=-\frac{L/2}{r}=-\frac{L}{2\, r}[/math] We know that the photon will traverse the length of the arc at the speed of light. The amount of time it takes for the photon to traverse this distance is [math]\Delta \tau[/math] as we have previously discussed. But instead of defining the equation for the change in angle as [math]c\, \Delta t / r[/math], we need to parameterize the equation such that the photon starts its journey when the parameter [math]u=0[/math] and has traversed the length of the arc by the time [math]u=1[/math]. We still preserve the speed of light and [math]\Delta \tau[/math] in that the parameter, [math]u[/math], only operates within the range of zero to one. This allows us to define the equations for the change in angles of the path of the photon as follows: [math]\Delta \theta_{u}=\frac{u\, L}{r}[/math] where [math]\left \{u \in \mathbb{R} \ | \ 0 \le u \le 1 \right \}[/math] [math]\Delta \theta_{up}=\theta_{min}+\Delta \theta_{u}=-\frac{L}{2\, r}+\frac{u\, L}{r}=\frac{L\, \left (2\, u-1\right )}{2\, r}[/math] [math]\Delta \theta_{down}=\theta_{max}-\Delta \theta_{u}=\frac{L}{2\, r}-\frac{u\, L}{r}=\frac{L\, \left (1-2\, u\right )}{2\, r}[/math] As expected, [math]\Delta \theta_{down}=-\Delta \theta_{up}[/math]. We can now substitute [math]c\, \Delta \tau[/math] in place of [math]L[/math] and arrive at the parameterized equation which describes the angles that the photon traverses for both paths. We will also redefine this angle as: [math]\Delta \theta_{\gamma}=\frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}[/math] Because the photon starts at the coordinate, {w, 0, y}, we can now define the equation which describes the path of the photon. Since we only consider the horizontal W axis and the vertical Y axis in our initial coordinate, the equation is simply that which defines a circle: [math]w'=r\, \cos \left (\pm \Delta \theta_{\gamma}\right )=r\, \cos \left (\pm \frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}\right )[/math] [math]y'=r\, \sin \left (\pm \Delta \theta_{\gamma}\right )=r\, \sin \left (\pm \frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, r}\right )[/math] Before we can substitute this result into the equation that we derived in the previous post for the path that traverses an expanding sphere, we must also parameterize all of the equations we have previously defined. Luckily, this step is easy to accomplish as we only have to replace [math]\Delta t[/math] in these equations with [math]\left (u+n\right )[/math]. The variable, [math]n[/math], defines integer multiples of [math]\Delta \tau[/math]. This is because we need to be able to advance the up and down paths of the photon by the amount of time it takes for the photon to traverse the length of the arc. We will also be using the modified [math]\Delta \tau[/math] versions of the equations for motion where [math]\mathit{Sl}_{0}[/math], [math]\mathit{Vl}_{S}[/math] and [math]\mathit{Al}_{S}[/math] notation will be used to represent the modified constants. We finally have all of the pieces to the puzzle (not including the mechanical clock)!!! The equations which describe motion in the form of uniform acceleration ([math]\Delta W[/math] defines the radius of the sphere): [math]\Delta W=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right )[/math] [math]\Delta X=c\, \Delta \tau\left (\mathit{Xl}_0+\mathit{Vl}_x \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_x \, \left (u+n\right )^2\right )[/math] [math]\Delta Y=c\, \Delta \tau\left (\mathit{Yl}_0+\mathit{Vl}_y \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_y \, \left (u+n\right )^2\right )[/math] The equations which describe the angles as the clock traverses across the expanding sphere (take note that [math]c\, \Delta \tau[/math] is canceled out as a result of the division): [math]\Delta \theta_x=\frac{\Delta X}{\Delta W}=\left (\frac{2}{2}\right ) \frac{\mathit{Xl}_0+\mathit{Vl}_x \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_x \, \left (u+n\right )^2}{\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2}=\frac{2\, \mathit{Xl}_0+2\, \mathit{Vl}_x \, \left (u+n\right )+\mathit{Al}_x \, \left (u+n\right )^2}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] [math]\Delta \theta_y=\frac{\Delta Y}{\Delta W}=\left (\frac{2}{2}\right ) \frac{\mathit{Yl}_0+\mathit{Vl}_y \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_y \, \left (u+n\right )^2}{\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2}=\frac{2\, \mathit{Yl}_0+2\, \mathit{Vl}_y \, \left (u+n\right )+\mathit{Al}_y \, \left (u+n\right )^2}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] The equations which describe the coordinates for the untransformed path of the photon (Describes what we perceive to be a stationary clock that is only moving through the temporal dimension): The photon path angles: [math]\Delta \theta_{\gamma}=\frac{c\, \Delta \tau\, \left (2\, u-1\right )}{2\, \Delta W}=\frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}[/math] The untransformed path of the photon (+ angles describe the up path and - angles describe the down path): [math]W_{\gamma}=\Delta W \cos \left (\pm \Delta \theta_{\gamma} \right )[/math] [math]Y_{\gamma}=\Delta W \sin \left (\pm \Delta \theta_{\gamma} \right )[/math] or [math]W_{\gamma}=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right ) \cos \left (\pm \frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}\right )[/math] [math]Y_{\gamma}=c\, \Delta \tau\left (\mathit{Wl}_0+\mathit{Vl}_w \, \left (u+n\right )+\frac{1}{2}\mathit{Al}_w \, \left (u+n\right )^2\right ) \sin \left (\pm \frac{2\, u-1}{2\, \mathit{Wl}_0+2\, \mathit{Vl}_w \, \left (u+n\right )+\mathit{Al}_w \, \left (u+n\right )^2}\right )[/math] The equations which describe the coordinates for the transformed path of the photon: The full non-simplified version: [math]w'=\left (W_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]x'=\left (W_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, \left (Y_{\gamma}\right ) \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, -\, \left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]y'=\left (Y_{\gamma}\right ) \, \cos(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, \left (W_{\gamma}\right ) \, \sin(\Delta \theta_{y})[/math] The simplified version with [math]\Delta \theta_{w}=0[/math]: [math]w'=\left (\Delta W\right ) \cos\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]x'=\left (\Delta W\right ) \sin\left (\Delta \theta_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] [math]y'=\left (\Delta W\right ) \sin\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}\right)[/math] We can also specify initial angles from which to start the path. This modification is very easy to do as shown below: [math]w'=\left (\Delta W\right ) \cos\left (\Delta \theta_{x}+\phi_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] [math]x'=\left (\Delta W\right ) \sin\left (\Delta \theta_{x}+\phi_{x}\right)\, \cos\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] [math]y'=\left (\Delta W\right ) \sin\left (\Delta \theta_{y} \pm \Delta \theta_{\gamma}+\phi_{y}\right)[/math] Images produced by graphing the equation: The rings that are seen in the images below are only used for reference points. The paths of the photons are the triangle like structures. The arcs that can be seen along with the photon paths are all of length [math]L[/math]. We can see from the images that this mathematical framework models space in such a way that it will eventually appear flat as time approaches infinity. This image shows two light clocks. One is moving outward with positive time and the other is moving outward with negative time (see page 2 posting #34 for an explanation of positive / negative time): This image shows one clock moving outward at [math]90^\circ[/math] from the other: This image shows acceleration in the clock that is moving through positive time (please note that I used extreme values for the acceleration so that I could produce this very cool image): This image shows a multitude of clock paths: This image is very interesting indeed as we get our first glimpse of the spiraling singularity: Next, we will use the completed equation and derive time dilation. After we have derived the time dilation equation, I will describe the singularity and post detailed images that I have graphed of it. Good night everyone. I hope that you all have enjoyed reading this thread, reviewing the mathematics, and looking at the images of the graphs : )
-
Temporal Uniformity
Thank you for the reference Pantheory. I will try to make time ; ) to explore all of the many theories that discuss time. I have considered what you have said about time in regards to an interval of change. I must conclude that you and I are debating two sides of the same coin. I have referred to motion in many of my posts as a mathematical description of a rate of change. Mathematics is purely abstract in that any motion is described as a rate of change. I relate this concept to the reality or concreteness of our universe as pure physical motion. With that being said, one can argue that both of our concepts are balanced through opposition and are one and the same no different than up is to down. So I will concede and define that time is as you specify, "an interval of motion / change" as these are both one and the same. One being mathematically abstract, the other realized in a concrete / physical sense. P.S. I was browsing the forums when I seen you posted. You can expect my e-mail tomorrow when I wake up as I will not post the remainder of the mathematics for another day or so to allow everyone to view and interpret the math. This will give you some time to review what I have derived so that you can prepare your responses to what I will post and how you might be able to use it in your theories.
-
Temporal Uniformity
I am going to let my posting tonight stand for a day or so. But, I will be more than happy to send you an e-mail of what I have so far as I do have your e-mail address. Right now my brother is demanding that I go and jam on the guitar with him, but I will send it to you as soon as I can : )
-
Temporal Uniformity
You are welcome Pantheory and I also agree that time can best be understood and explained by definition alone. However, temporal uniformity is not just concerned with explaining the phenomena of time. The purpose of the mathematical framework that is being set forth is to redefine the Lorentz factor and show how we can begin to explain even more complex phenomena as a result. The mathematics and graphs that I will be posting may be of some interest to you as they do produce vortices. I understand that your latest thread, Pushing Gravity, deals with such things in the aether.
-
Temporal Uniformity
I am familiar with the phenomenon, aberration of light. The mathematics set forth does not conflict with this phenomenon as our space is practically flat as supported by the mathematics. Perhaps we can discuss this phenomenon in detail after I have presented this mathematical framework to see how well it fits vs. observation or we can start a new thread regarding that discussion. Also, could you please edit your quote of my latest post to not include the entire posting as you are only referring to my repsonse to your statement. Thank you : )
-
Temporal Uniformity
That is correct Michel. The concept that I have been examining is that where a four dimensional sphere is expanding through all dimensions. Perhaps I wasn't clear in explaining how we perceive this four dimensional sphere. But to try and respond to your statement, it is true that we are enclosed locally in an expanding three dimensional sphere. The 4D distance that you are referring to, only explains why massive bodies do not speed up or fall behind us temporally. If this 4D distance was not uniform for all observable bodies, then these bodies would either appear or disappear from our view of the universe. Continuing with the discussion, we now have to define the parametric equation that describes a path across that of a sphere. For this we must use trigonometry. Before we can define this equation, we must start by defining a line segment as an arc that traverses across the surface of the sphere. The equation for the length of an arc across a sphere with radius [math]r[/math] can be derived as follows (We will simplify this example by examining a circle): The circumference of a circle is given by: [math]2\, \pi \, r[/math]. The angle, in degrees, encompassing the arc is proportional to [math]360^\circ[/math] where [math]\frac{\theta^\circ}{360^\circ}[/math] defines the percentage of the circle that the arc traverses across. This allows us to calculate the length of the arc by multiplying the circumference of the circle by this ratio: ArcLength or distance, [math]d=\frac{2\, \pi \, r\, \theta^\circ}{360^\circ}=\frac{\pi \, r\, \theta^\circ}{180^\circ}[/math] Now that we know how to calculate the length of an arc, we must solve for [math]\theta[/math]. This is because [math]\theta[/math] changes as a body traverses across the sphere or circle. [math]\theta^\circ=\frac{180^\circ \, d}{\pi \, r}[/math] We can simplify this result by converting degrees to radians (When referring to an angle from this point on we will always be using radians as it truly simplifies the mathematics): [math]\theta_{rad}=\left ( \frac{\pi}{180^\circ} \right ) \frac{180^\circ \, d}{\pi \, r}=\frac{d}{r}[/math] We discussed the equations for motion in the previous post and can now substitute that result for the variable, [math]d[/math], in the above equation which describes the angles that such motion produces as a body traverses across the sphere. The hypothesis states that this sphere is expanding at the speed of light. This means that the radius, [math]r[/math], of the sphere is expanding at the rate [math]c[/math]. However, we will substitute [math]V_w[/math] because it represents the temporal velocity that we have been discussing since the beginning of this thread. We will also define the motion of this expanding sphere no different than how we have defined motion in the previous post. This results in allowing temporal acceleration for completeness. However, this does not imply that we accelerate through time as it is hypothesized that this temporal acceleration, [math]A_w[/math], is now equal to zero. The reason for including it is so that we can experiment with inflation which states that the universe expanded faster than the speed of light during its initial birth as hypothesized by Alan Guth in 1980. If inflation did in fact occur, then it would be possible to have temporal acceleration. However, we will not be discussing inflation at this time. It is important to understand that our measurement of time in this mathematical model is nothing more than a count of cycles as provided by some form of clock. We can convert these cycles to seconds by using a conversion factor, frequency, as previously discussed. This results in mathematical time as being calculated by taking the distance travelled and dividing it by the speed at which such distance was traversed. With that being stated, it is still proper to define time with the variable, [math]t[/math], which is equivalent to: [math]time=\frac{cycles}{frequency}=\frac{meters}{meters / seconds}[/math] Combining everything discussed, we can now derive the equation which describes [math]\Delta \theta[/math] for a body as it traverses across the surface of an expanding sphere. We will use the standard equation for uniform acceleration from which we will substitute our modified [math]\Delta \tau[/math] version in later. The equation which describes the motion along the axis S: [math]\Delta S=S_0+V_s \, \Delta t+\frac{1}{2}A_s \, \Delta t^2[/math] The equation which describes the motion of the expansion of the sphere: [math]\Delta W=W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2[/math] The change in angle that such motion produces as a body traverses across the expanding sphere: [math]\Delta \theta_s=\frac{\Delta S}{\Delta W}=\frac{S_0+V_s \, \Delta t+\frac{1}{2}A_s \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] Now that we can calculate the [math]\Delta \theta[/math] for such motion we can define the parametric equation which describes the path of the body starting from the coordinate, {w, 0, y}: [math]w'=w \, \cos(\theta_{yaw}) \, \cos(\theta_{pitch})\, -\, y \, \cos(\theta_{yaw}) \, \sin(\theta_{pitch}) \, \cos(\theta_{roll})\, +\, y \, \sin(\theta_{yaw}) \, \sin(\theta_{roll})[/math] [math]x'=w \, \sin(\theta_{yaw}) \, \cos(\theta_{pitch})\, -\, y \, \sin(\theta_{yaw}) \, \sin(\theta_{pitch}) \, \cos(\theta_{roll})\, -\, y \, \cos(\theta_{yaw}) \, \sin(\theta_{roll})[/math] [math]y'=y \, \cos(\theta_{pitch}) \, \cos(\theta_{roll})\, +\, w \, \sin(\theta_{pitch})[/math] The coordinate, {w, 0, y}, is the starting position of the photon that travels between the reflective surfaces of the light clock. The angle, [math]\theta_{yaw}[/math], is a rotation about the vertical Y axis and describes the angle that changes as the clock traverses what we perceive to be the X axis. We will redefine [math]\theta_{yaw}[/math] to be [math]\theta_x[/math] to avoid confusion between which angle causes horizontal translatory motion along the X axis. The angle, [math]\theta_{pitch}[/math], is a rotation about the horizontal X axis and describes the angle that changes as the clock traverses what we perceive to be the Y axis. We will also redefine [math]\theta_{pitch}[/math] to be [math]\theta_y[/math] to avoid confusion between which angle causes vertical translatory motion along the Y axis. The angle, [math]\theta_{roll}[/math] is a rotation about the W axis. We will redefine [math]\theta_{roll}[/math] to be [math]\theta_w[/math] as it defines the angle of rotation for the mechanism in a mechanical clock as will be discussed much later. The above parametric equation is derived by multiplying the rotation matrix for each axis in a specific order that describes the angles as yaw, pitch and roll. The equation can also be derived by applying the following equation, which describes the rotation of a point about a specific axis, in the same manner as the matrices: [math]x'=x \, \cos(\theta)\, - \, y \, \sin(\theta)[/math] [math]y'=x \, \sin(\theta)\, + \, y \, \cos(\theta)[/math] Now that we have our equations which describe the changes in angles and the path across a three dimensional sphere, we will end this post with the following summary: The equations which describe motion in the form of uniform acceleration: [math]\Delta W=W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2[/math] [math]\Delta X=X_0+V_x \, \Delta t+\frac{1}{2}A_x \, \Delta t^2[/math] [math]\Delta Y=Y_0+V_y \, \Delta t+\frac{1}{2}A_y \, \Delta t^2[/math] The equations which describe the angles as the clock traverses across the expanding sphere: [math]\Delta \theta_x=\frac{\Delta X}{\Delta W}=\frac{X_0+V_x \, \Delta t+\frac{1}{2}A_x \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] [math]\Delta \theta_y=\frac{\Delta Y}{\Delta W}=\frac{Y_0+V_y \, \Delta t+\frac{1}{2}A_y \, \Delta t^2}{W_0+V_w \, \Delta t+\frac{1}{2}A_w \, \Delta t^2}[/math] The parametric equation which describes a path across the sphere: [math]w'=w \, \cos(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, y \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, y \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]x'=w \, \sin(\Delta \theta_{x}) \, \cos(\Delta \theta_{y})\, -\, y \, \sin(\Delta \theta_{x}) \, \sin(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, -\, y \, \cos(\Delta \theta_{x}) \, \sin(\Delta \theta_{w})[/math] [math]y'=y \, \cos(\Delta \theta_{y}) \, \cos(\Delta \theta_{w})\, +\, w \, \sin(\Delta \theta_{y})[/math] The next posting will complete the mathematics presented in this post by deriving the equations which predict the coordinates that a photon in the light clock traverses for both the up and down paths. I will also be posting images of the graphs that these equations produce for the path of the photon. We will discuss [math]\Delta \theta_w[/math] when we get to the point where we are describing the path for a mechanical clock. For now, we will set [math]\Delta \theta_w=0[/math]. Once we have completed the mathematics which describe the path that light from a light clock takes as it traverses the expanding sphere, we will substitute our equations for motion that make use of [math]\Delta \tau[/math] and derive the time dilation equation. Please keep in mind that even though I have made great effort to ensure that the mathematics that I have posted is correct, I have been known to reverse and mix things up from time to time. Also, my grammar isn't the best in the world : ) Everything that I have posted has been graphed and verified using Mathematica. With that being said, please message me if you do find an error so that I can make the appropriate corrections. Thank you.
-
Temporal Uniformity
On The Temporal Uniformity of Accelerating Bodies The view that is to be set forth attempts to describe the universe from the point of view of a four dimensional sphere that is expanding at the speed of light. We can simplify the equations by breaking this sphere into two, three dimensional, spheres. This results in one sphere being comprised of W, X and Y axes, and the other dealing with W, Y and Z axes. The W axis is the spatial dimension of time and is shared along with the vertical axis, Y, between both spheres. If one considers that we exist on the surface of such spheres, then we can take a section of each sphere and combine them to form our three dimensional view of the universe. The spheres would be aligned such that one sphere provides the X, Y plane and the other provides the Y, Z plane. Because the curvature of a circle or sphere diminishes as the radius increases, and due to the enormous size of these spheres, our space will appear to be flat. Also, we would lose the W dimension because the four dimensional sphere is expanding at the speed of light and length contraction would have collapsed the fourth dimension to have no perceivable length. For the sake of simplicity, we will only consider the W, X and Y sphere. This will allow us to derive time dilation equations across what we perceive to be a two dimensional plane. The purpose of exploring time dilation for the path of a clock as it traverses across the surface of an expanding sphere is to derive the mathematics for the Lorentz factor which is affected by such surface which is not flat. We will explore the paths for a light clock and a rotating mechanical clock and show that both approach the equation for time dilation as defined in SR as time, and subsequently the radius of the sphere, approaches infinity. The equations that are to be discussed are not new and by no means considered complex as they simply deal with the basic mechanics for motion as defined in classical physics. The equations that will be discussed will include uniform acceleration and we will begin by discussing Newton's interpolation formula as it allows us to derive a single equation for simple motion that is only dependent on the locations of a body along its trajectory. This allows us to extend the equations for motion beyond that of uniform acceleration. Newton's interpolation formula can be written using the binomial theorem as follows (The locations of a body's trajectory combine in such ways that use binomial coefficients when interpolating such simple motions. We can also use the Gamma function to generate these coefficients): [math]\sum_{i=0}^{n-1} \left [ \sum_{j=0}^{i} \left [ \left ( -1 \right )^{j} \binom{i}{i-j} S_j \right ] \times \binom{i-t-1}{i} \right ][/math] The variable [math]n[/math] is the number of measurements or specified locations, [math]S_j[/math] is the location specified by the [math]j[/math] index, and [math]t[/math] is time. It is important to note that the locations are sampled within equal intervals of time. As a bonus, I will post the interpolation formula for locations sampled at any given time once we have completed this journey : ) If we let [math]n=1[/math], the formula yields the initial position [math]S_0[/math]. When [math]n=2[/math], the formula yields the equation for motion as defined by the initial position and velocity: [math]S_0 +\left (S_1 - S_0\right )t[/math]. Finally, we can derive the equation for uniform acceleration by specifying [math]n=3[/math] which yields the following: [math]S_0 + \left (\left (S_1-S_0\right ) - \frac{1}{2} \left (S_2-2\, S_1+S_0\right )\right ) t + \frac{1}{2}\left (S_2-2\, S_1+S_0\right )t^2[/math] We can see from the above results for [math]n=3[/math], that we can easily derive the constants for acceleration and velocity as follows: [math]a=\left (S_2-2\, S_1+S_0\right )[/math] [math]v=\left (\left (S_1-S_0\right ) - \frac{1}{2} \left (S_2-2\, S_1+S_0\right )\right )[/math] However, this does not help us derive time dilation as we need to define acceleration, velocity, and the initial position in terms of the time it takes for light to travel between the reflective surfaces of a light clock that are separated by a length [math]L[/math], or the distance [math]\left \vert AB \right \vert[/math]. This results in redefining the locations, [math]S_j[/math], in terms of [math]L[/math] such that [math]S_j=\mathit{l}_j \times L[/math] where [math]\mathit{l}_j[/math] is a length scalar or multiple of [math]L[/math]. The amount of time it takes light to travel between the two reflective plates of a light clock is equal to [math]\Delta \tau = L / c[/math] such that [math]L = c \, \Delta \tau[/math]. Substituting this result back into Newton's interpolation formula allows us to completely factor out [math]c \, \Delta \tau[/math] as follows: [math]c \, \Delta \tau \sum_{i=0}^{n-1} \left [ \sum_{j=0}^{i} \left [ \left ( -1 \right )^{j} \binom{i}{i-j} \mathit{l}_j \right ] \times \binom{i-t-1}{i} \right ][/math] We can now reconsider the constants of acceleration, velocity, and initial position when [math]n=3[/math] as follows: [math]a=c \, \Delta \tau \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )[/math] or [math]a=c \, \Delta \tau \ a_l[/math] where [math]a_l=\left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )[/math] [math]v=c \, \Delta \tau \left (\left (\mathit{l}_1-\mathit{l}_0\right ) - \frac{1}{2} \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )\right )[/math] or [math]v=c \, \Delta \tau \ v_l[/math] where [math]v_l=\left (\left (\mathit{l}_1-\mathit{l}_0\right ) - \frac{1}{2} \left (\mathit{l}_2-2\, \mathit{l}_1+\mathit{l}_0\right )\right )[/math] and [math]S_0=c \, \Delta \tau \ \mathit{l}_0[/math] [math]S_1=c \, \Delta \tau \ \mathit{l}_1[/math] [math]S_2=c \, \Delta \tau \ \mathit{l}_2[/math] It is important that [math]\Delta \tau[/math] is completely factored out. Otherwise, it will get trapped inside the parametric equations which describe the path that light from a light clock takes as it traverses across the expanding four dimensional sphere and we would not be able to derive time dilation accordingly when using the arc length integral to calculate the length of the path. The usage of Newton's interpolation formula to describe simple motion will only be used in this post as we will only concern ourselves with uniform acceleration. The reason for discussing this equation was so that we can establish a foundation for which simple motion of any form, including that beyond uniform acceleration, can be used to derive the time dilation equation and ultimately the Lorentz factor. Next, we will apply the equation for uniform acceleration to a light clock that is traversing across an expanding sphere. But, that is for the next post.
-
Temporal Uniformity
Perhaps you are correct Pantheory and time is nothing more than an interval of change. However, I ask you to consider what is change? We typically think of change as an explanation for why something is different than how it was, but this does not clearly define why something changes or how it has changed. If we dig deeper into the mechanism of change, we will find physical motion as the cause. This can be demonstrated in that a change in a body's position is caused by the motion of the body relative to our own position. The erosion of a landscape is caused by the motions of matter and energy as it applies forces upon the land that it is acting upon. Even when considering sources of change that do not seem to have motion, such as that of the wave of colors produced by electrochemical processes in a cuttlefish, there is always an underlying mechanism which is in motion that produces such change. The colors in our clothing fade due to exposer to photons and chemicals which strip the pigments from the material. I can continue to list many more examples of things that change. The point is that we will always find that it is actual physical motion that drives change. That is my reason for not accepting that time is just an interval of change because it is physical motion that drives change and not change that drives physical motion. If we take the example where we can define time by dividing the distance traveled by the speed at which we traversed such distance and then place ourselves in the rest frame where our displacement and speed equals zero, then when we try to determine our time we get a division by zero which is undefined. One could state that this is a relative matter but we are still left with mathematics for which only works if we are in fact in motion relative to something else. This mathematical paradox of an undefined time for the rest frame of reference can only be resolved if we consider that we are always in motion through the dimension of time and that we do indeed traverse a physical distance through this fourth dimension. I now have internet and my ISP has provided me with web space to upload the images I have created so that we can continue this discussion and explore the mathematics that I have derived as explained earlier in my posts. I understand that this mathematical framework does not assure that the theory is correct, nor does it mean that temporal uniformity will gain acceptance by my peers as Swansont has pointed out. However, a theory without a mathematical basis is forever doomed to failure as it cannot provide us with a means to check the validity of such theory. A good theory not only provides us with definitions that describe the mechanics of the universe, but provides us with the means to rule it out by checking its assertions as provided by the mathematics. I will start by breaking the mathematics into simpler components from which I will make seperate posts describing the mechanics of each component. Once all of the equations have been defined I will assemble them together and post the images that they graph along with a link to the Mathematica file that I have produced so that everyone with Mathematica 5.2 or greater can reproduce the graphs and images. We will begin the discussion this week once I have set up my web space and have uploaded the images and files that I will be posting : )
-
Temporal Uniformity
Sorry I haven't been active in a long time. I have everything ready to post but I cannot find a site that will host the images so that I can link them directly to my posts. If someone knows of a good site that will allow me to upload the images so that I can link them here, I would appreciate it. Otherwise, I will have to wrap everything up in a PDF file and upload it to Google Docs so that I can provide a link.
-
Temporal Uniformity
Thank you for changing the thread title MooeyPoo. I just didn't want this thread to be confused with the "time" poll thread or its author.
-
Temporal Uniformity
When you consider that motion can be defined as frequency times meters per cycles, or: [math]f \frac{m}{cycles}[/math] We can clearly define the mechanics of time as a statement of the total distance traveled divided by the distance traveled within an interval of oscillation where frequency is the time conversion factor and cycles represent our measurement or unit of time. Let's say that we traveled 3 meters within one interval of oscillation as provided by a pendulum. The pendulum is not tuned to oscillate within an interval of a second and therefore each oscillation is a measurement of time of its own temporal unit as provided by the pendulum. We can use a conversion factor, frequency, to convert the cycles of the pendulum to seconds, but this is not as important as the distance traveled within the interval of oscillation. If our speed remained constant, and we lost our pendulum, then we could divide the distance traveled as stated by our odometer, with the fact that we travel 3 meters within the interval of oscillation and derive the time, in units of the pendulum's cycle. 300 meters divided by 3 meters / cycle equals 100 cycles of the pendulum. If the frequency of the pendulum was tuned so that one cycle equals one second, or frequency equals one, then a total of 100 seconds would have passed for the 300 meters we traversed. In essence, any measurement of time is actually a statement of the total distance traveled divided by the distance traveled within an interval of oscillation. Since we know from the equations of relativity and that of temporal uniformity, that we move through the fourth dimension of space at the speed of light, then we can use an oscillator and calculate the distance traveled through this fourth spatial dimension. The same principles work for all other observable spatial dimensions as stated previously and as shown in the above example using the pendulum. The equations and plots that I will be posting in a week or two, clearly demonstrate these principles. I have successfully derived time dilation in accordance to the path that light from a light clock traverses across an expanding four dimensional sphere. I have checked my new equations against the equations for time dilation in special relativity. My equations produce near identical results and converge to the equations of relativity as our distance through the fourth dimension, or time, approaches infinity. This is a result of the diminishing curvature of a sphere or circle as it gets larger and larger. The equations also produced something that was unexpected, a singularity that spirals towards time zero of the big bang. This is a result of light racing around an extremely small sphere that has just started to expand. As time progresses, the light can no longer complete the journey around this expanding sphere due to the size of the sphere itself. This results in the light path tapering off from a spiral to progressing in straight lines away from the singularity as the universe expanded. Also, I have calculated the maximum viewing angle, based on the speed of light, that we can see across this expanding sphere. This results in our space as being an isolated three dimensional sphere that is expanding away from the Big Bang at the speed of light. Granted, I have not considered any other physical forces or constants except that of the speed of light. However, I will make a conjecture that this spiraling singularity should form a ring singularity once these forces are added into the equations and QM affects are considered. Also, one must consider Occam's razor which suggests that we should tend towards simpler theories which provide explanations regarding the subject matter at hand. This does not imply that my theory of temporal uniformity is correct, but instead shows that we should consider temporal uniformity because it provides simple explanations for all phenomena of time which is based on the accepted theory of relativity.
-
Temporal Uniformity
I have been extremely busy getting ready to go back to OU this fall. I do not have internet at the moment and am using a friends computer to post this message. I have more of the mathematics worked out and I will post the results as soon as I get moved into my new apartment. Everything has been done with Mathematica and I will post the equations and images of the plots so that you all can reproduce my results. I must say that you guys are in for a real treat : )
-
Temporal Uniformity
Ok I couldn't resist. I will give you guys a hint. I better not .
-
Temporal Uniformity
Swansont, I do realize and respect the arguments that you have made in regards to QM and time. I appreciate you taking time to debate the topic. I hope we all have a little better understanding of what time may be. The question is definitely not answered with 100% certainty. But if we do discover temporally displaced mass-energy, then this will have huge implications. A huge part of my theory uses Bose-Einstein condensates. Check out this discovery made by physicist at the University of Bonn in Germany. I hypothesize that the singularity at the heart of every black hole is a super-photon or Bose-Einstein condensate of mass-energy in some form. Since we know that light is related to electron - positron pairs at high energies, then it could be possible that the singularity is actually a matter Bose-Einstein condensate associated with an anti-matter Bose-Einstein condensate. Once black holes throughout the entire universe consume all of the mass and energy, space collapses and causes all of the black holes from the center of galaxies to come back together at time zero at the center of the big bang. This falls in line with the principles of temporal uniformity because of the hypothetical Einstein Rosen bridges, or wormholes that may exist inside supermassive black holes linking two or more points in three-dimensional space or through the [math]w[/math] axis of space-time. The warping of space due to all of this mass-energy would cause these two condensates, at the center of the singularity, to collapse into each other resulting in another big bang. The condensates could form in a similiar manner as shown in the experiment that the physicists at Bonn have conducted. Except the massive pressure induced by the collapsed space inside the singularity provides the cooling effect as it restricts the motion of particles or waves allowing for the condensates to form. However, this third part of my theory is purely speculative. But, it does allow us to derive a theory of quantum gravity that is based on GR, QM, and temporal uniformity. Once I have created such model, I will be able to determine the validity of these extended claims unless the hypotheses I made towards dark-matter is observed in star wobbles, giving validation through observation. Considering the consequences of this view, it may be possible that Hawking radiation does not evaporate supermassive black holes at the center of galaxies. The virtual anti-particles caught in the event horizon that fall in would either be absorbed by the anti-matter condensate, or if it collided with the matter condensate it would just be converted back to light and be split up between both matter and anti-matter condensates where the process repeated in a chain reaction until this new mass-energy was distributed equally. This would work identically for the virtual matter particles. We could also further hypothesize that any form of mass-energy transforms into a super-photon that splits into matter / anti-matter pairs due to the acceleration from falling towards the singularity. This would allow both matter and anti-matter condensates at the heart of the singularity to always be balanced and it provides an explanation for the cause of the big bang. Therefore, infinity is expressed through recursion in cycles of big bangs and the finite quantity of space-time and mass-energy is conserved. Thus my general theory of temporal uniformity pretty much relates all things that exist in the abstraction of mathematics to the reality of our concrete physical universe and even though it may be wrong, it appears to be balanced. Since no one has pointed out why it is incorrect or proved it wrong, then my claims stand. I would be happy to retract my claims in light of other truths. It does not mean that I would abandon the theory altogether. It just means that I could align my thought process towards the facts and derive new hypotheses accordingly. I make this conjecture towards supermassive black holes because the current accepted theories tell us micro black holes will evaporate. However, we cannot ignore the implications of what it would mean if my view is correct and that we cannot destroy a singularity once it has been created. This means that the LHC could actually end life on Earth due to micro black hole creation which may not actually evaporate. Not to be superstitious but 2012 is next year and the LHC keeps increasing the levels of energy used in collisions. However, the scientist predict that it will be 2014 before the LHC runs at full power and current theories support black hole evaporation. I just want to end with this; "extraordinary claims require extraordinary evidence", Carl Sagan. I have actually constructed a device that is very extraordinary and it is not an anti-gravity device or anything as such. But once the patents go through, I can reveal what it actually is and it is quite remarkable. I believe it embodies everything I have debated to be true and the evidence that it does exist is hard to deny.
-
Temporal Uniformity
Because of the law of balance, I believe that it may be true that length cannot by reduced to zero as a result of a mathematical tranformation of actual physical space. There must always exist some distance in between any two points. Anyone who has taken calculus knows this because of having to calculate integrals using the Riemann sum. Applying the same concept to deriving points in space, shows that there will always exist some distance in between any two infinitesimal points. The universe implements this abstract mathematical concept, of a physical distance always existing between two points, using mechanics that drive the cosmological constant. This would explain the anti-gravitational effects we observe for these things. This is why I posed the question here on this site, "Quantization of Length? Heresy or Merit?". These questions are important because they affect the underlying space-time metric. The Lorentz transformation affects all aspects from length contraction to time dilation. If we know that the current metric that we use does not properly describe all apsects of physical space, then we must consider such questions and hypotheses that affect this attribute to space-time. Combining all of my proposed ideas allows us to redefine gamma as: [math]\gamma=\frac{1}{\sqrt{1-\frac{v_{r}^{2}}{c^{2}-v_{w}^{2}}(1-l^{2})}}=\frac{1}{\sqrt{1-\frac{(v_{r} + v_{r} l)(v_{r} - v_{r} l)}{(c + v_{w})(c - v_{w})}}}[/math] Where [math]v_{r}[/math] is the relative velocity perpendicular to the temporal axis, [math]v_{w}[/math] is the temporal velocity relative to time zero at the center of the big bang (equals zero with respect to the time-normal and time-relative frames of reference), [math]l[/math] is the length quantization number (which could actually be zero), and [math]c[/math] is the speed of light.
-
Temporal Uniformity
Dimensional Collapse A Thought Experiment on Obtaining Light Speed When dealing with the construct of the universe it is necessary to use the microscope of the mind to gain insight into the problem at hand. We will take a journey on a spaceship that is designed to test how light speed affects our vision. Our scientists have invented a device that, for the purpose of this discussion, allows two astronauts to defy relativity and reach the speed of light. Taking into account the dangerous nature of this mission, the two astronauts prepare their estates, take care of any last minute business, and say their good byes to their friends and family. Because according to relativity, if the anti-relativity device fails, they could end up being crushed into a singularity as a result of having infinite mass. The day finally arrives and the two astronauts pilot the spaceship to the location where the test is to begin. After some time of acceleration along their flight path, the two astronauts finally obtain light speed. At the point in time they obtained light speed, both astronauts looked at the other in anticipation of celebrating the moment. It is at this moment, the anti-relativity device malfunctions. For sake of discussion, we will not be so cruel as to crush our astronauts into a singularity by observing the effects of relativity. However, the view has changed entirely for our astronauts. According to special relativity it takes an infinite amount of energy to reach the speed of light. We must also conclude that the reverse is true and, unless the anti-relativity device begins to function properly, our astronauts are now forever trapped going the speed of light in the direction they are traveling. We must also conclude that all motion, in the direction the spaceship is traveling, has been restricted to a plane perpendicular to the direction of forward motion. This is because special relativity states that nothing can go faster than the speed of light. So our astronauts can only move in the direction of up, down, left, or right. All forward and backward motion would be impossible and because our astronauts were looking at each other, they would also notice that each appear to the other as a vertical strip. This is because we have two eyes and since our astronauts are traveling at the speed of light, they can only see light perpendicular to the direction they are moving. Since the brain combines the images from our eyes to form a single image with the perception of depth, our astronauts would really see each other as a single vertical strip. For all intents and purposes, both astronauts actually appear to be two dimensional in how they view each other and how they are restricted to movement along a two-dimensional plane. They are experiencing dimensional collapse in the direction of motion and because of the definitions in relativity, they also appear two dimensional to observers on Earth. The consequence of dimensional collapse is a reality of the Lorentz contraction and combined with the constancy of the speed of light, we can explain how we experience time. Even if the astronauts could move around freely, they would not be able to see the light from anything behind them in the direction of motion. And if everything else in the universe was also moving at the speed of light parallel to and in the direction of their motion, they would not be able to see the light from anything in front of them. Due to dimensional collapse from the Lorentz contraction, they would be restricted to only being able to view the universe along dimensions that are perpendicular to their motion. The speed of light accounts for why we cannot see objects in the future or past, and the Lorentz contraction collapses the dimension of time to where it is no longer perceived to have any length and restricts us by no longer allowing us to traverse forward or backward in the direction of motion. This means that the future and past would be nothing more than physical points along the spatial dimension of time where all observable phenomena co-exists at a definite point along with all other non-observable phenomena existing at different points along the temporal dimension, all traveling with uniform direction at the speed of light. If we apply the same scenario as explained above to a four dimensional space where all matter and energy are co-moving at the speed of light along a spatial dimension, such as the dimensional axis the astronauts are traversing, then we can account for having three spatial dimensions and one temporal dimension. Since the astronauts are now traveling at the speed of light through four-dimensional space, the temporal axis collapses and we are left with three observable spatial dimensions. This is logical because mathematics defines that all spatial dimensions share a common origin point and must be perpendicular to each other regardless of number. The previous statement only holds for Euclidean space as it is not referring to projected or transformed spaces. Since the speed of light is constant, both astronauts would forever be at rest with each other along the temporal axis and could only perceive their forward motion through time by observing motions through dimensions perpendicular to the temporal axis. And because they would no longer be able to observe objects in front of them or behind them, they would no longer be able to measure their forward velocity in the traditional sense as they would not have a reference point to measure their motion against along the collapsed temporal dimension. If for some reason both our astronauts developed amnesia and could not remember their initial velocity, they would have to derive a new way to measure their forward motion as they can no longer physically move or see along the dimensional axis they are traversing at the speed of light. This is identical to how we experience time, as a perceived forward motion, with no reference to the velocity, distance traveled, or physical size along the temporal axis, while existing in three-dimensional space. Thus we are restricted to only being able to see and interact with the objects that co-exist with us at our point in time. The only way we could measure our forward motion through time, is by using a device with a mechanism that can oscillate with intervals of known length along the dimensions perpendicular to the forward motion. If the astronauts recovered from their amnesia, they could remember that they are traveling at the speed of light. And even though they can no longer perceive the dimension in the direction of their forward motion, they could use an oscillator of specified interval, along with the rediscovered knowledge of their velocity, and calculate the distance they traveled. We can also deduce why our space is nearly flat. This is because if the entirety of space is curved, as shown in the image from an earlier post visualizing the big bang, then light would travel along this larger curvature of space. We can only percieve this large curvature as straight lines due to the nature of light. The gravitational lensing from super massive bodies that bends light and show us that space is curved, warps the existing topology of this larger curvature comprising the entirety of space allowing us to see that space is warped. But this does not mean that we should be able to look out through the entirety of space and see this larger curvature. Another way to think about this is from the stanpoint of space being shaped as a sphere. Since light must follow the shape of space and we use light to measure lines, then we would be able to see galaxies and stars on the other side of this sphere. If space didn't expand faster than the speed of light, we would eventually and "theoretically" be able to see the entire history of Earth from start to end (as long as we weren't on the planet when it ended : ) This shows how the universe deals with infinity using a finite amount of space and mass-energy. Law of Balance We can also argue that the primary law of the universe is balance in the form of opposition. Even though we cannot completely prove assumptions based on the law of balance, we can still determine if our thought process is balanced. From this I can state, "The opposite of dimensional axes where I have the freedom to change my speed and direction and where I can perceive size in the form of width, height and length, is a single dimensional axis of space where I do not have the freedom to change speed or direction and where I cannot perceive any physical length along the restriced axis. Therefore, space and time are balanced through opposition. Space gives rise to time and time gives rise to space. They are one and the same no different than how up is the same as down. I understand that this view is more a philosophical one, but the logic can also be applied to science and religion. Science and religion are both philosophies which are opposite in nature. Science demands belief by evidence and religion demands belief by faith. Therefore science and religion are balanced through opposition. Religion gives rise to science which in turn gives rise to religion. But even if the law of balance cannot directly prove a statement, we can show that it holds true for all things. This can be demonstrated in the fact that if there was no up, there would be no down. If there was no religion, a philosophy where belief is governed by faith, then how could science exist? The fact that science demands belief based on evidence shows that its opposite, belief based on faith, must also exist. Because, we could not define one without the other. This is why the law of balance is so important. It provides us with a way to do consistency checks on our logical pathways no different than that of a computer. Swansont could use the law of balance to argue that motionless physics, QM, is balanced by opposition in relation to classical physics where motion is realized. He would be partially correct in that definition. But this is also where balance can be misinterpreted by thinking in opposites and explains why we cannot use it for the basis of a proof. Physics is based on mathematics and from this fact it would be better to say, "Mathematical space, being a set of motionless points, is opposite in nature from motion that moves through these points in space. Therefore, space and motion are balanced by opposition and are one and the same. Space gives rise to motion which in turn gives rise to space. You cannot have one without the other. This may not seem logical to most people. But the truth is that we move through space because all points in space have distance between them. You may try to argue that space can exist without motion but then how could you explain the big bang from the standpoint of a singularity? It is a dimensionless point. There are no other points one could move to and if motion did not exist, there would be no distance between the points in any metric space. Motion can only exist if there are distances between points, so a space that has distance between points implies motion because we now have a distance to move through. It is the same paradox relating to, "What came first? The chicken or the egg?". The only truth is that the chicken and the egg are opposite in nature. Therefore the egg gave rise to the chicken which in turn gave rise to the egg. You can't have one without the other. We call the science the explains how the egg derived the chicken, evolution, and the science of biology explains how the chicken derives an egg. We can infer that if there exists opposites that must simultaneously exist, such as up and down, then there are also opposites that are not simultaneous (one must come before the other). But you still cannot have one without the other. This is what I meant by stating that [math]f(x)[/math] implies motion along the [math]x[/math] or [math]y[/math] axis. This explains "why" the space in our universe is actually expanding. Balance is a binary mathematical relationship that stores information about the existence of any and all things and It would be impossible to store any type of information if the law of balance did not exist or hold true. This is as stated before, without up you cannot have down. The fact that up and down does exist, adds an informational bit to the structure of the universe. But it does not tell us "how" a physical system works or allow us to make statements about the accuracy and precision of the measurements we can make within the physical system. You cannot have physical space with distances between points without motion extending these points, and according to Swansont, QM works without motion in regards to atomic clocks. I asked him to remove all "motion" from the physics for which QM is based on and show that we can still have QM. Even though he may be completely 100% correct in his definitions for QM, if we removed all physical motion, even time, then QM would not exist. Therefore this idea of QM requiring no motion at all to measure time, is not balanced.
-
Temporal Uniformity
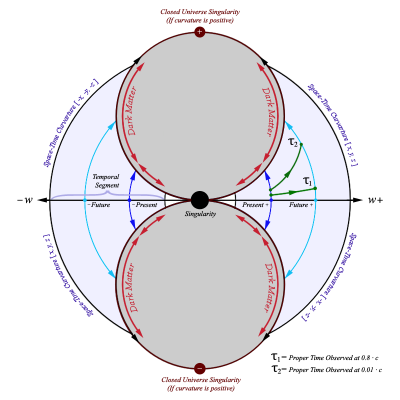
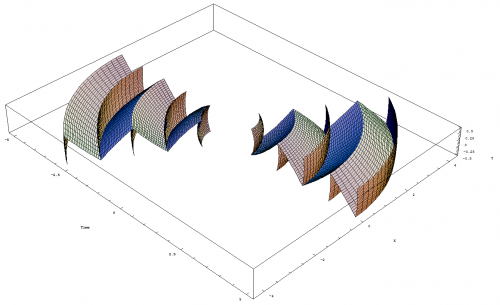
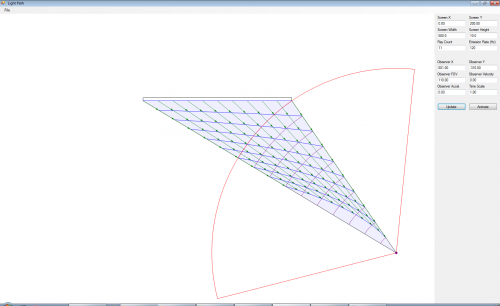
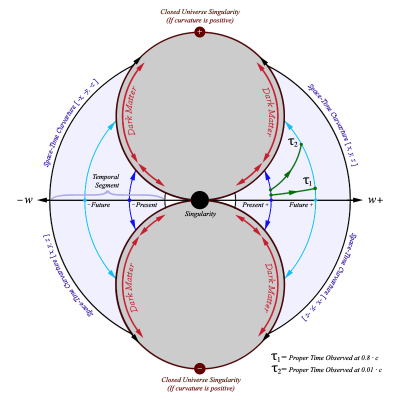
Considering that my theory deals with time from the point of view of SR / GR, that it is improper to compare such theory to QM when the theory does not make any assertions to QM. To this date no one person has proved a link between SR / GR and QM that would allow us to make such assertions. Furthermore, the mathematics complements the framework as defined in SR and does not conflict with relativity in any way. Unless the mathematics or the logic can be proven wrong, I recommend that we elevate this speculation to the status of being a valid scientific theory for which will be the basis for the "Principle of Temporal Uniformity". This theory will suffice for the attainment of a simple and consistent theory of the temporal uniformity of rigid bodies as pertaining to temporal displacement which would result in altering the past in any way that would affect the present or allow the transmission of information from either the future or past into the present. The notion of temporal displacement in regards to being able to travel forwards or backwards through time to alter the present is impossible as the view here developed will not allow one to travel through time in such a way that would allow them to view or interact with the same matter and energy from their original point in time. It shows that the notion of being able to travel to any time, that only exists as a memory of the past, or will exist as a memory in the future, is impossible. I must also ask you to consider the attached image I provided earlier. This view of the universe aligns itself with all aspects of mathematical spaces. We can see that the image demonstrates a relationship between three dimensional space to a fourth dimensional time axis. The birth of our universe is centered at the origin of the coordinate system and there is an imaginary psudeo-fifth dimensional axis that goes through the positions of the closed universe singularities due to space-time curvature. The true nature of mathematics is one of recursion and not that of heuristic shortcuts which simplify the equations. We cannot construct a universe from math without including all aspects of which is entailed in mathematics. This can be logically deduced as follows: "Mathematics cannot exist without the universe and the universe cannot exist without mathematics. Therefore the universe gave rise to mathematics which in turn gave rise to the universe. In short, the proof comes from the fact that if it was impossible to do mathematics in a universe no different than ours, then this universe would exist as a paradox unto itself because the beings that inhabit it would still be able to group, identify, count and measure objects that exist in their universe. If the true laws of physics were known by these beings, then they would be able to deduce the existence of other universes and therefore these other universes are observable even if they are void of life. This is a complicated way of saying that every mathematical property and relationship must have existed at time zero or before the birth and expansion of our universe and because life exists in our universe, then the laws that govern life also existed at the creation of the universe. Who am I to say what form this life took before my universe was created when I do not know the mathematics which govern it? The only truth I can derive is that the universe is so perfectly balanced that it is also unbalanced." When you begin to consider all the possible options, whether you believe in a big bang that was created as M theory proposes or any other theory, you have to consider black holes as the source for the big bang. I am working on the mathematics that shows the shape of the universe from the point of view of a spherical shaped singularity, based on the Schwarzschild radius, that exploded along an arbitrary spatial dimension simliar to gamma ray burts, quasars, and pulsars. This arbitrary spatial dimension is the axis of space we call time and the outer edge of the sphere to the center represents the length of the temporal segment. I have already worked out the mathematics that shows the field lines of each layer radiating away from the singularity. Oddly enough this idea is based on mathematics that I have been developing that shows the field lines that light from an image form to reach an observer. I've transfered this concept to the shape of a sphere where we consider the inverse of the mathematics as shown in the image I have attached to this post and allows for the cosmological constant to govern the expansion. The green vectors are all of equal length, the blue lines represent the photon fields, and the purple arcs represent the light we see instantaneously. The triangle represents the observer's field of view. The photon fields extend from negative infinity to positive infinity and have a horizontal asymptotic relationship with the dimension along the width of the screen, or any other geometrical shape that emits / reflects an image. Once I am done, I should have a good estimate for the geometry of space because the photon field lines would represent the space we exist in and I can substitute any geometrical shape in place of the singularity. I will post the mathematics once I am done. The following parametric equation is incomplete but does allow us to produce the image below: [math]x_{\{t,u\}}=t-(I_{y}-u) \frac{t}{\sqrt{t^{2}+I_{y}^{2}}}[/math] [math]y_{\{t,u\}}=I_{y}-(I_{y}-u) \frac{I_{y}}{\sqrt{t^{2}+I_{y}^{2}}}[/math] The variables [math]t[/math] and [math]u[/math] are the parameterized inputs, [math]I_{y}[/math] is the screen's [math]y[/math] position with the [math]x[/math] position being located at zero, and the observer is at the origin.
-
Temporal Uniformity
My original point can be summarized as follows: When we measure motion, we are actually making a statement about a rate of change in the measurement of distance travelled. For example, to state that we are traveling at 100 m/s, is to declare that one hundred meters will be measured for each second of time measured. This defines a relationship between distance and time in terms of speed. It is a relationship that is expressed as the physical measurement of the distance traveled within an interval of oscillation of known length as provided by a clock. This leads us to the conclusion, that motion in terms of velocity or acceleration, is actually a statement of directional motion compared to a rotational or cyclic motion. This allows us to mathematically redefine motion in terms of frequency times distance traveled per unit cycle, [math]f \times m / cycles[/math], which is exactly what we are doing when we measure motion using clocks. This can be demonstrated using dimensional analysis as follows: [math]v = \frac{m}{s}=f \times \frac{m}{cycles}[/math] [math]f = \frac{cycles}{s}[/math] [math] \frac{m}{s}=f \times \frac{m}{cycles}=\frac{cycles}{s} \times \frac{m}{cycles}=\frac{m}{s}[/math] [math]time=s=\frac{cycles}{f}[/math] Where [math]v[/math] is velocity, [math]cycles[/math] is the number of oscillations, [math]f[/math] is the frequency of the oscillation, [math]m[/math] is meters, and [math]s[/math] is seconds. Before we can interpret our motion through time as having a velocity, we must understand what it means to have velocity. This is because we measure our motion through space with respect to our motion through time. Therefore, when we try to measure our velocity through the temporal dimension we can only obtain a normalized velocity of one. This is a result of how we measure speed as a change in space over a change in time and, according to relativity, is the same as measuring a change in space over a change in fourth dimensional space. We could use any dimensional axis as a replacement for time. The only difference is that we have the ability to change our speed and direction in the other spatial dimensions, creating consistency issues with this pseudo-temporal dimension. This leads us to the conclusion that, even though motion through time is the same as motion through space, we cannot measure our speed through time in the same manner that we do for space as a result of [math]dt / dt[/math]. This is why we are forced to measure motion through time using constant oscillations of known intervals. Oscillation allows us to normalize our measurements of motion through time. The fact that we measure time in seconds is irrelevant because this unit of measurement is just an interval of oscillation that we have created to measure the passage of time. A second could have lasted for any length of duration. However, it is the relationships imposed on these measurements which are important as they define the mechanics that describe the universe. The mathematics I posted near the beginning of this thread supports this notion of time as demonstrated in the attached image from my post above yours: We can see from the attached image that the observers, at [math]\tau_{1}[/math] and [math]\tau_{2}[/math], would radiate away from the big bang frame of reference at the speed of light frozen in place along the temporal segment. We can show that the space-time vectors, with the head at each observer's position and the tail remaining at the center of the singularity at time zero, is equal in magnitude. This means that no matter how fast each observer moves in directions perpendicular to the axis of time, each observer will remain "radially" frozen along the temporal segment radiating outward from the big bang frame of reference at the speed of light, with a relative temporal velocity of zero with respect to each others frame of reference as shown by the mathematics. The result of which does not refute the possibility of temporally displaced mass-energy. This is because the magnitude of the space-time vectors as defined from the big bang frame of reference to the observer's frame of reference, can be used to determine which "universe" the observer is located in. Furthermore, because I related all three frames of references to each other we can use the following relationship to show that even though both observers experience time differently, they are moving through time equally from the big bang frame of reference. From the big bang frame of reference, both observers place themselves in the time-normal frame of reference placing the other in the time-relative frame of reference. So from the big bang frame of reference both observers have a zero relative velocity, [math]V_{r}=0[/math], and experience the time equally: [math]\Delta t_{b} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{0^{2}}{c^{2}}}=\Delta t_{b} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}}[/math] However, I do not imply that this proves that mass-energy is temporally displaced. Therefore, I have provided science with a way to test this hypothesis: Have I not followed the scientific method? I base my claims on existing characterizations of the subject matter being discussed as SR and GR deals with space and time. I stated a hypotheses about a theoretical notion to the nature of time. I derived mathematics from which lead to a prediction which can prove the hypotheses true or false. And, I have submitted my theory for peer review so that scientists, astronomers, and cosmologists can conduct experiements based on my predictions.
-
Temporal Uniformity
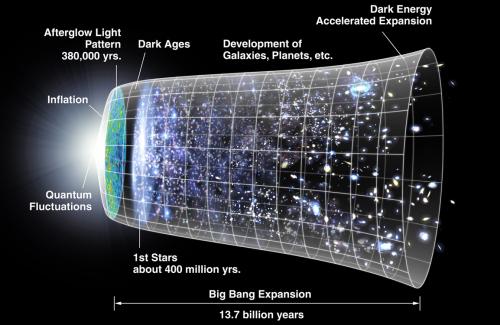
If we look at the second half of my hypothesis in regards to temporally displaced mass-energy, we must consider the big bang and the metric expansion of space. The following image from wikipedia inadvertently demonstrates temporally displaced mass-energy: From this view of the universe we can see our own unique history radiating away from time zero of the big bang. The vertical slices in the image above are different points through the fourth dimension, time. We can also view the vertical slices as temporally displaced parallel "universes" all co-moving at the speed of light in a uniform direction through time. These "universes" would just be different views of our single universe. Each universe would have its own unique history because any observer located along the temporal axis could record events using space-time coordinates that would be unique to their view of the universe. We could also show that time should be bi-directional. Even though SR may not perfectly describe the metric of space, we know that it involves functions that specify a rate of change that includes square roots. Mathematically, square roots have two solutions. However, it is customary to choose the solution that satisfies the physical system. If we make a conjecture that the big bang expanded space in a similiar manner that a gamma ray burst, or quasar radiates energy into space along both directions of an arbitrary spatial dimension, then we can interpret the results of the mathematics by introducing positive and negative time as shown by an image I produced to visualize the concept:
-
Temporal Uniformity
For anyone wondering what started this debate in regards to the inference of motion, I have pasted the hypothesis from the original post below:
-
Temporal Uniformity
Sure it is when you consider that you cannot, with 100% certainty, measure the length or position of such object. This can be shown with the laws of thermodynamics. Since a body's temperature affects the QM state of the atoms, the matter either contracts or expands. So the length of the body is in motion with respect to temperature. You would not only have to calculate the length and trajectory of the body from your choosen frame of reference, but you would also have to account for QM affects to even be able to determine the center of mass for the body to be able to tell me the object's true position or size in relation to your choosen coordinate system. I have not described motion using any form of classical physics. I never said that position, length, or any other quantity can be determined absolutely. That is an assumption you made by not clearly reading my posts. It may be that I have not properly explained myself. Regardless of your stance, you cannot dismiss my claims by stating such things without demonstrating why or how I have used such notions in physics in a classical, non-modern way. Also, you have not shown any mathematics to support your claims. Am I to believe that you are free from the burden of proof and that this only applies to me or anyone else that proposes theories that might not necessarily fit within your current views on Physics? My point is simple in that QM uses a metric mathematical space which represents our physical universe. Because physics makes assertions and claims using the abstraction of mathematics, you cannot say that [math]f(x)[/math] does not imply physical motion. This is because the input [math]x[/math] implies motion along the [math]x[/math] axis of the mathematical space that QM uses to describe its processes. Therefore we can infer motion from functions operating in mathematical spaces that represent our physical world. I could use any physical process, classically defined or accepted by modern science, and still arrive at the same conclusion regarding motion. Motion is still infered even from your own arguments of the deBroglie matter wave as you cannot describe the deBroglie Matter Wave without velocity or any other form of motion. This implies that motion is still an integral part of QM from which you cannot ignore or get rid of by dismissing my comments. And, the Heisenberg uncertainty principle is only true because motion exists. We cannot relate such simple HS mathematics to the mechanics which describe the laws of nature. When dealing with abstract notions of a definite static length, position, or any other classically defined notion, we must accept that these are pure mathematical abstractions and cannot be used to describe the universe with 100% certainty. Plus any mathematical functions you choose to describe a physical system are inherently bound to describing the rate of change for such functions with respect to the input or output of the function. Let me clarify a relevant point on the topic of rates of change. When looking at any form of [math]d?/d?[/math] with the concept that this rate of change represents a physical process, then the mathematical construct which represents the rate of change becomes a description of physical motion whether it is related to time, temperature, or any other physical quantity. I understand that you are referring to motion as defined below: However, I must ask you to consider that we can infer motion in relation to time even when stating rates of change that do not describe its motion or change with respect to time. This is because, as mentioned in Wikipedia, motion signifies any temporal change in a physical system. Therefore I can imply that any physical rate of change is motion in relation to time regardless if the physical rate of change uses time or not. Because you relate motion with respect to time is irrelevant. I can relate my displacement along the [math]x[/math] axis to any other physical quantity because the physical system from which this quantity is defined relates such quantity to time. This means that I could use the rate at which a given species of bacteria reproduces as the basis for my time keeping device. Therefore I can relate my [math]x[/math] position to the number of bacteria in my time keeping device. I can also relate any other physical quantity to the [math]x[/math] position of a car that I am riding in instead of using time. I could state that for every meter I travelled along the [math]x[/math] axis, that I measured a displacement of two meters along the [math]y[/math] axis. The reason why we do not do this is because we cannot derive consistent relationships which can describe such mechanics in an accurate and precise way. This is why time works for our purposes and gives us an explanation as to why we can always describe rates of change with respect to time. This is because regardless of our frame of reference, we cannot choose a coordinate system where motion through time can no longer be implied. If you claim that you can, then by all means go live at a position defined by that coordinate system. You will live longer : ) So my statement regarding motion still stands: Unless you can show that you can define the wave function without using any form of metric space and functions from which we can infer motion through that space, then the above statement holds true. Time can be considered as motion through a spatial dimension no different than the other three observable spatial dimensions. The only reason why we relate motion to time is that we are expanding with the big-bang through all spatial dimensions. We can deduce that we move at the speed of light through the fourth dimension. I explained this near the top of this thread. Plus, AJB was nice enough to demonstrate how we can arrive at my same conclusion using physics that I have yet to learn. From the big-bang frame of reference, a coordinate system that is always positioned at time zero in the center of the big-bang, we can deduce that we move at the speed of light through the dimension of time. If we choose this coordinate system, we can state that the space we are moving through is stationary or vice-versa. This means that the Lorentz contraction would have collapsed the dimension of time to having no perceivable length. This explains why we are unable to see the objects temporally displaced from our position in time. It also gives us a reason for why it is nearly impossible to displace our position temporally due to the constancy of the speed of light. Plus, if mass-energy is temporally displaced it would move at the same rate as we do through this fourth dimension of space. There is one way to test this theory. If we observe a star that wobbles as if locked into a binary star system and we cannot detect this other star, then based on the wobble of the star to rule out any other cosmic possibilities we can determine if mass-energy is truly displaced temporally. Otherwise, it will either require a consistent theory of quantum gravity or solutions in cosmology that solves the dark matter, energy, and flow problems, to prove or disprove this notion. Even though my knowledge of physics may not be equivelant to yours, you cannot deny the logic in the statements I have made in regards to motion and mathematics. I know that you all do not know me very well and, as such, I must prove myself. When I find some extra time, I will post some of the mathematics that I have derived. I mainly work in game theory, probability and statistics, and finite calculus and numerical analysis as required by the industry for which I have based my career. You are more than welcome to read about it in my profile. On a seperate matter, how often do you get a theory proposed in the Speculation group where there is math to support it and the author provides a way for you to check to see if the second half of his hypothesis, temporally displaced mass-energy, is true or false by observing the motions of stars in the heavens?
-
Temporal Uniformity
Plus you have to be able to show why this is false The short hand version is that [math]\frac{dx}{dt}[/math] is no different than [math]\frac{dx}{dy}[/math], or [math]\frac{dx}{dx}[/math], and you cannot define a function, [math]f(x),f'(x),f''(x)[/math], etc... such that I am unable to infer motion as a rate of change along the axes of the specified mathematical space. This would mean that you would have to be able to describe QM without a mathematical space and use functions from which I would not be able to infer motion.