Enthalpy

In case the electron had a rather well defined direction before the slit, it implies that its lateral position wasn't so precise. A slit narrower than the width of the previous electron's wavefunction (the lateral position) makes the wave narrower if the electron passes through, and then the electron's direction is less defined, so the electron can be detected in a position that was not attainable to it before it passed the slit. This is described in more details for light and is called "diffraction", so you can read for instance the Wiki articles. Electrons do the same for being waves too.

Please remember that a patent is nothing more than a proof that you might use before judges. It doesn't prevent anyone to infringe your invention. In that case, a patent only serves if you're willing to go to court. This can be lengthy, expensive, and random. If an infringing company is in China, Brazil or the US you must go to a court there, and need a patent in said country. Applying for a patent is already expensive, then you must pay very year to keep the patent. This holds for every country, and you must provide the text in all the languages (the EU simplifies that a bit). So do it only if you're wealthy enough. Most patents bring money only to the governments and patent attorneys.

The way I understand it, the bent wire is immobile versus B while the skewed one, of identical nature, moves and is in contact with the bent one. d(flux)/dt gives an induced voltage (with a sign) while the summed wire length gives a resistance. Neglecting the self-inductance (="the field produced by the wires themselves") you get a current. Note that 8T is unusually strong. It take a superconductor or a small duration. 32ohm/m is much even for a resistor wire.

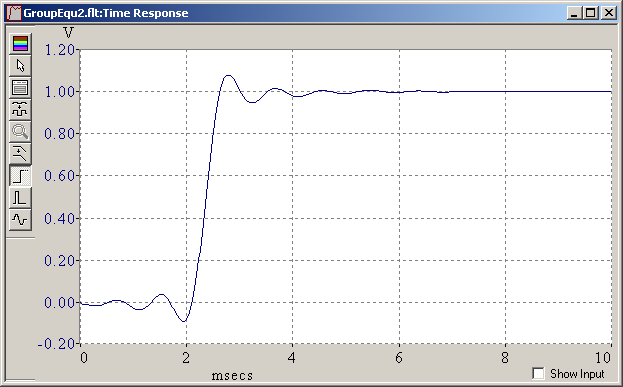
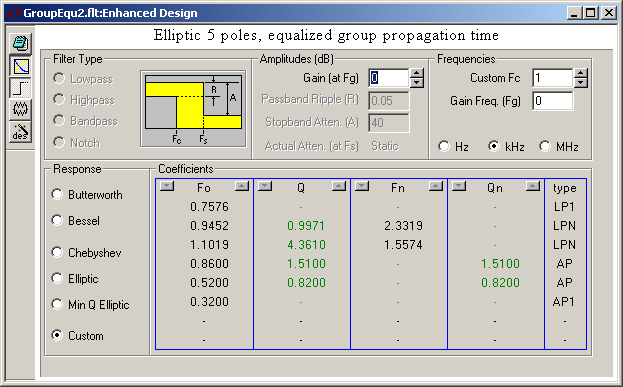
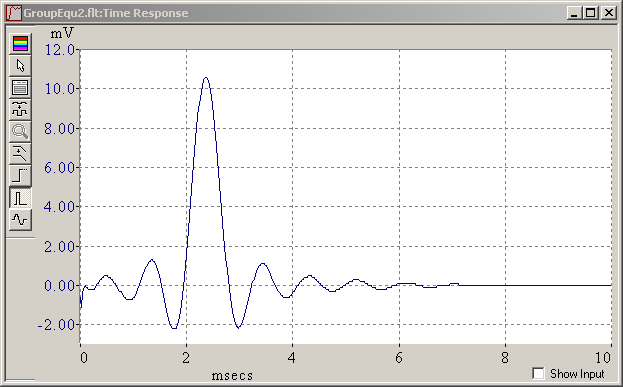
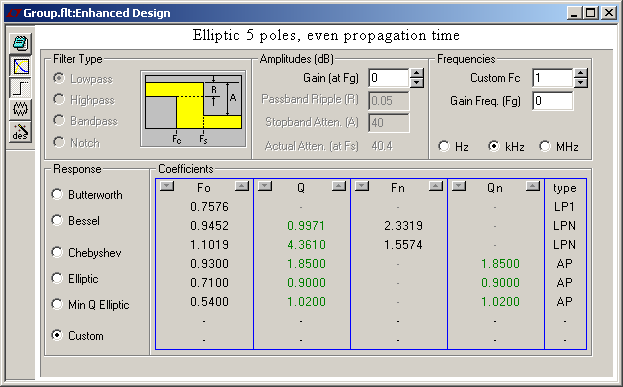
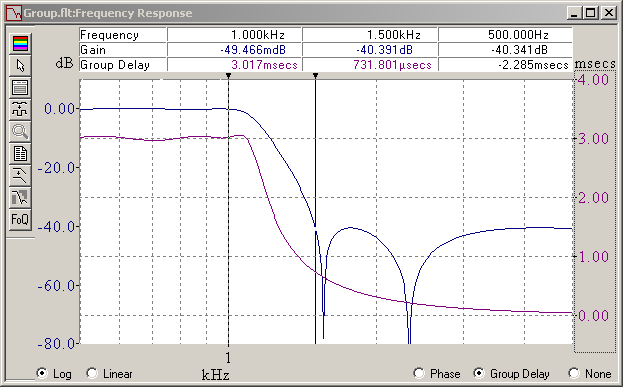
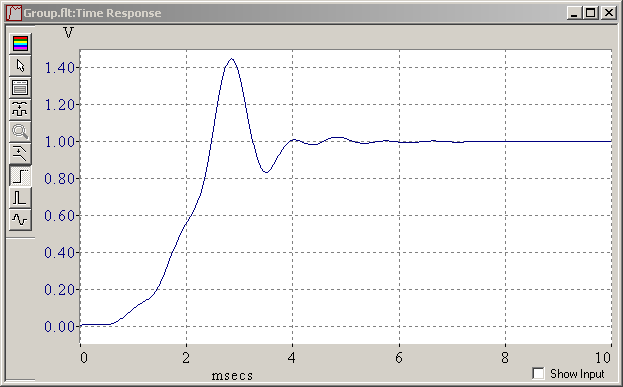
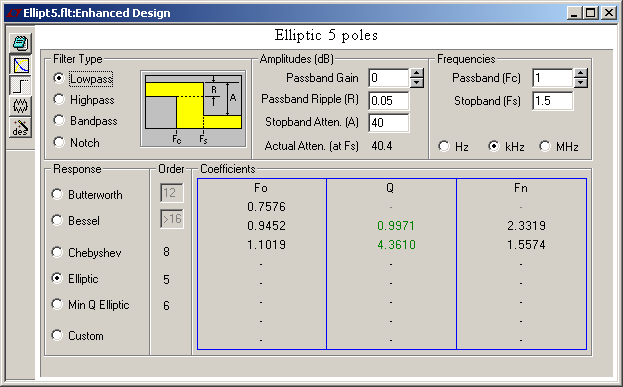
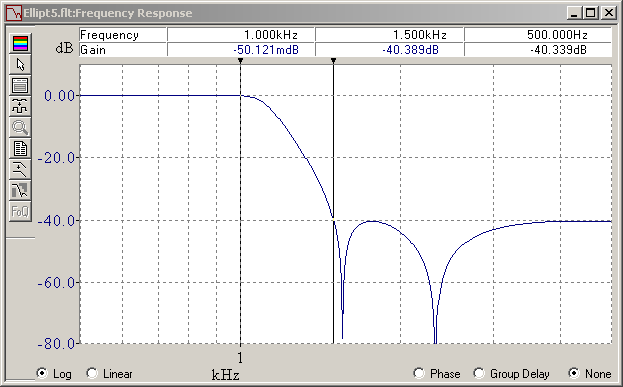
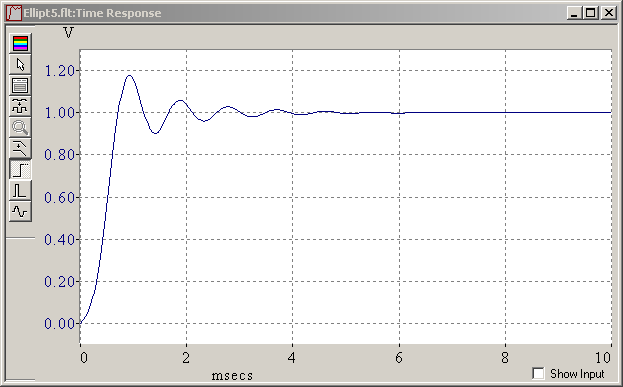
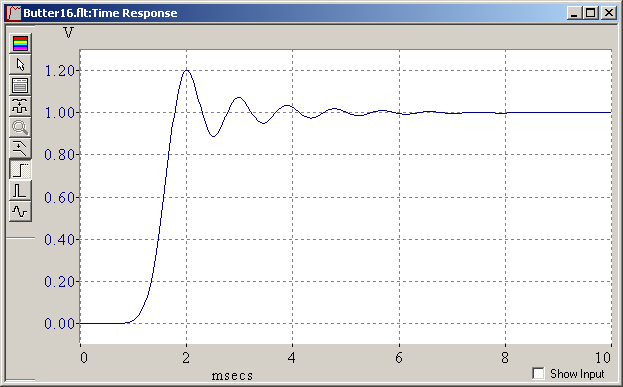
And I was wrong. Equalizing the group delay time works, at least in a first approximation. My mistale was that I had never observed frequencies low enough. Equalizing only 2-3 octaves below the cutoff doesn't suffice and made the time response unbalanced. This is again the 5th order elliptic low-pass, with a 5-pole phase corrector, tuned if not perfectly, and its impulse and step responses: Tuned phase correction cuts in half the ringing amplitude but adds as much before the main transition, in one pulse per corrector pole. This improves much the visual impression on a real filtered signal. A quieter filter keeps its advantage after phase correction. The phase corrector adds group delay below the peak around the cutoff frequency. Above is useless. If keeping the peak in the group delay at cutoff, the filter still delays the signal by as much, but the time response isn't quite pleasant. A nicer time response results from more corrector poles, which increase the group delay up to the cutoff included, and increases the signal delay. On a recorded signal, the delay can be compensated, but then the filtered signal begins to wobble before the raw one. As can be seen above, best symmetric ringing needs a somewhat uneven group delay, more so with fewer corrector poles, and needs hand tuning, which isn't finished here. A continuous time filter or IIR can't be really symmetric, since its response is finite on the left. Marc Schaefer, aka Enthalpy

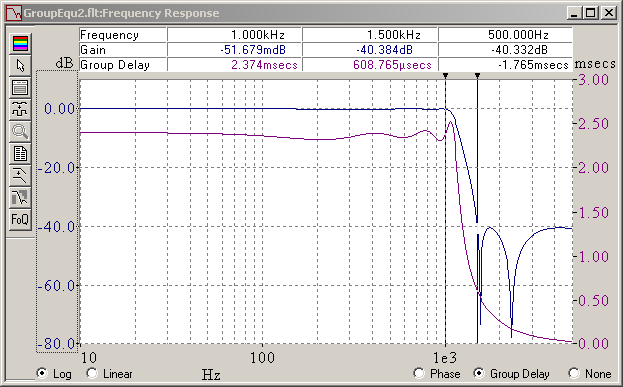
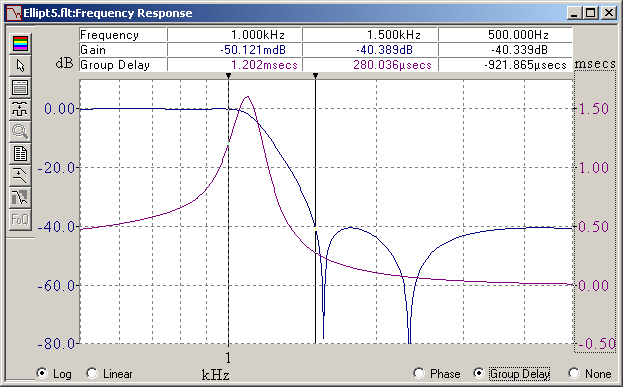
To improve the step response, a phase corrector is the answer. It appends a few second-order and possibly first-order "all-pass" cells, active or passive, which let the phase rotate around some frequency but leave the amplitude uniformly untouched. But how to tune these all-pass cells ? The universal answer, in all books and courses, is "make the propagation group constant in the passband", or equivalently, "make the phase linear". This is inspired by the pure time lag, whose propagation time is constant and phase linear. At digital FIR filters it works. Either I've understood zilch, or all these authors just repeat something that sounds good but they have never done, because each and every time I tried that way, it failed miserably. As a hint, I have never-ever seen an example of step response by those who recommend a constant propagation group from the phase corrector. Not a single time. So here's a example of failure. I first repeat the frequency response of the 5th order elliptic lowpass, this time with the group delay displayed, where you see the typical big bump around the corner frequency. Then I append three second-order allpass cells and optimize for uniform group delay in the passband. And then the step response is megayuk, much worse than the bare filter. More cells above the corner frequency don't improve. I plan to show a successful phase corrector on that elliptic filter. Marc Schaefer, aka Enthalpy

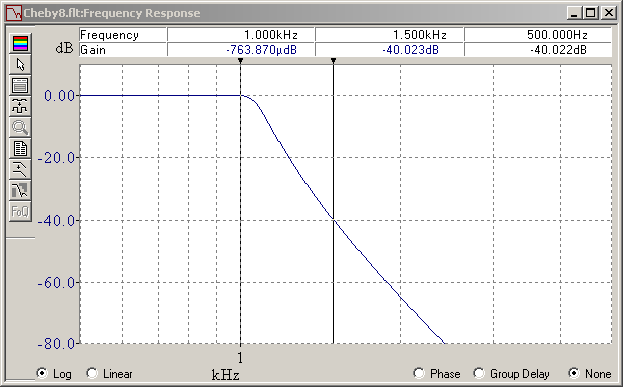
And this is an elliptic (or Cauer) filter that fulfils the same requirements. With five poles and two notches, it isn't simpler to build than the Chebyshev, but it reacts sooner and steeper than both the Butterworth and Chebyshev, and it rings for shorter. Maybe I put an inverse (or type II) Chebyshev here some time. It rings clearly less and for shorter than the elliptic, very similar to an hourglass filter. But as none is native to FilterCad, it takes me longer. Marc Schaefer, aka Enthalpy

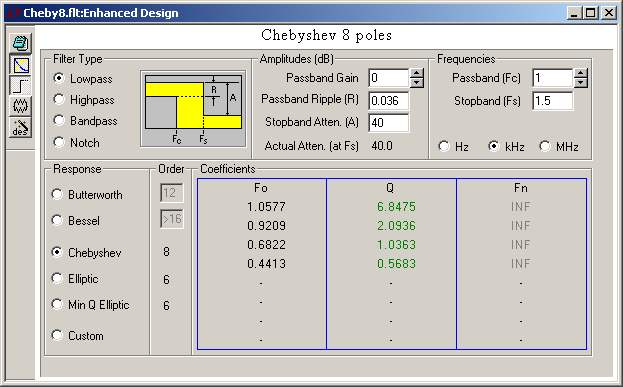
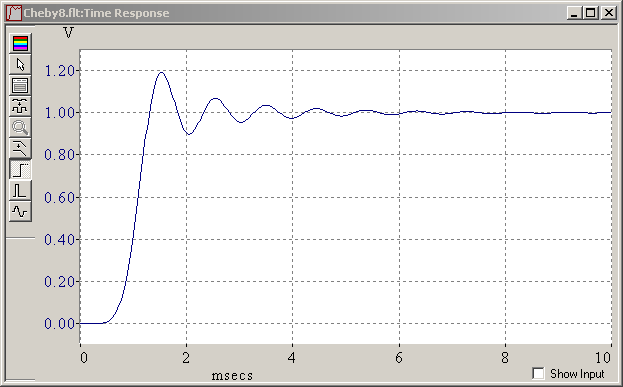
Here comes a Chebyshev with the same passband and stopband requirements. It rings for as long, but it reacts sooner and steeper than the Butterworth, and is half as complex. Marc Schaefer, aka Enthalpy

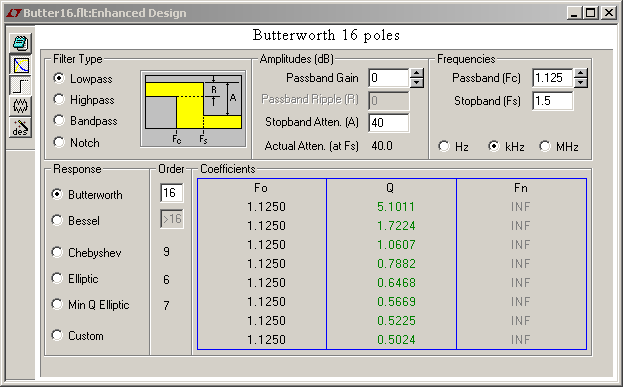
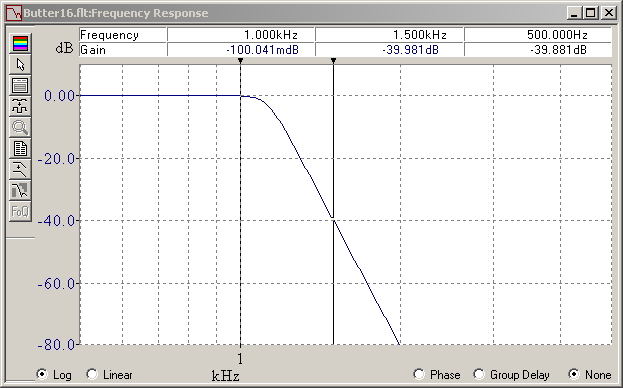
I use the excellent FilterCad 3.0 software that Linear Technologies made nicely general filtercad.software.informer.com The application is said to run on recent Windows after helping the installer a bit. The first case is a Butterworth. It has 16 poles because the competitors need less. While -3dB is meaningful for audio applications, metrology and present datacomms demand more. Here 0.1dB attenuation or ripple in the passband, which equals 2% power or 1% voltage, is more realistic. This is not the usual "corner frequency" of a Butterworth given at -3dB. The big Butterworth gives unimpressive 40dB attenuation at 1.5* the passband edge, which shall be the definition of the stopband and its attenuation for the other transfer functions. For its built-in transfer functions, FilterCad determines automatically the poles and zeros and draws the frequency and step responses. Marc Schaefer, aka Enthalpy

If the generator shall provide one positive and one negative smooth pulses per turn, it's called a two-poles alternator. Then the good design lets a magnet be the rotor, and the coil surrounds it at the stator. Called Gramme design. Check the drawing there https://en.wikipedia.org/wiki/Alternator https://en.wikipedia.org/wiki/File:Alternator_1.svg Iron at the stator is useful, among others to shield the world from the dangerous magnetic field, but with rare-earth magnets the iron is not mandatory for a decent induction.

Same query as Studiot. Looks quite feasible, but needs more information. Desired stability, what voltage, possibly temperature range, and so on.

Hello everybody! Frequency filters lets signals within the passband through and attenuate everything in the stopband, for instance noise or an adjacent communication channel. Much theory exists for them, works nicely. The stopband attenuation can be big, and the "selectivity", the ratio of the nearest frequencies of the stopband to the passband surprisingly small. But as the frequency response gets sharper, the time response gets slower and bumpier. No wonder, since a Fourier transform links them, like the diffraction rings of a lens, or the noise created by jpeg compression, or Delta(t) and Delta(E) for a particle. I'll consider only lowpass filters here. They are the most common, and only their time response makes much sense for the eye. Simple theorems only restrict the quickness (vague) of the filter for a given selectivity, not how much it rings. But as a typical filter rings at the extreme frequency of its passband, both seem related. The time response of a filter matters in some uses, for instance if you observe shocks with an accelerometer. Then the frequency response can't be too sharp. But some kinds of filters, or "transfer functions" out(F)/in(F), offer a better compromise than others. All the books and courses I know compare the step response of varied transfer functions at identical number of poles - identical complexity more or less. Then, the Butterworth is quietest, the Chebychev is in between, and the elliptic is bumpiest. The Bessel shows no overshot but filters too badly for most uses. (There are a dozen well-known named transfer functions). But the aim of a filter is not to build a cetain number of poles! It must fit some passband with a maximum attenuation there and some stopband with a minimum attenuation. Then an elliptic filter needs fewer poles than a Chebychev that needs fewer than a Butterworth. When comparing at identical constraint on the frequency response, hence with different numbers of poles, I claim that the step response of a Butterworth is bumpier than a Chebychev and an elliptic is quieter. Examples shall follow. Marc Schaefer, aka Enthalpy

In the first message, the link to (previously Dartigalongue) Sophie Dervaux playing Saint-Saëns' sonata is broken, but here's an other record: i0M1AIDLX8Y at 39:50 the very caring pianist let the bassoon play at a reasonable volume hence with a softer sound. The difference with the narrower French bassoon played by Julien Hardy remains.

Jazz on a bassoon is uncommon, not least because bassoonist are scarce. The instrument has strong arguments: easy emission, very easy articulation, comfortable air consumption, flexible tone height and... OK, its weak voice is a bad drawback next to a drummer, and the fingerings aren't quite fluid. But it swings better than a saxophone! The examples on Youtube are from Alexandre Silverio and co - few others exist. Here in usual small formations Invitation - Chorinho pra ele - Alone together that's a duet with himself Vou vivendo and here the Camaleon bassoons My favorite things - Take five - In a sentimental mood they are the bassoonists of São Paulo state symphonic orchestra.

A high input resistance doesn't always result in high noise. In a Jfet or Mosfet for instance, we use to take the inverse of the transconductance to compute the voltage noise produced by the transistor itself, at least at frequencies where 1/F noise gets negligible. Then you have the noise at the input impedance, which sees the signal source in parallel (often a lower resistance than the amplifier), and which can be shorted by the varied capacitances, depending on the frequency and the compared values. With piezoelectric or with capacitive sensors, at frequencies not very low, the capacitance uses to dominate. Then the voltage noise drops strongly. One can use for noise voltage and currents the standard computations. A big resistance provides a small noise current sqrt(4kTB/R) that gets shorted by the parallel capacitance. Then, the noise is minimized by a bigger resistance that produces a smaller noise current. This is the reason for my proposed bias or feedback using photodiodes there https://www.scienceforums.net/topic/88763-photocurrent-bias/ when no bias correction is needed, the conductance is essentially zero, removing this noise source. In an instrumentation differential amplifier, the resistances defining the gain are not connected to the sensor, and their noise is not shorted by the sensor's impedance. Their noise add to the source's and amplifier's ones. That's why application notes tell to use small ohmic values. When the amplifier's input is shorted by the signal source, the smaller resistance applies, or better, the combination of both. This often means that the noise of the source remains, and the amplifier adds some. The goal of a low-noise amplifier is to add little noise. Sometimes the source produces less noise than its equivalent resistance at 300K. This is typically the case for antennas over roughly 300MHz. Having low losses, they convert little feed power to heat as a transmitter, so their temperature produces little noise as a receiver (thermodynamics). Most of their noise is picked from the surrounding and converted efficiently. A dish antenna at 6 or 10GHz pointing to the sky picks little noise from its main lobe, and while it may show resistive 75ohm or 300ohm, its "noise temperature" is much lower than 300K, rather 100K. Than a quiet preamplifier is much more important. 1dB rather than 2dB noise figure (where 0dB refers to 300K) makes more than 1dB difference in the noise. Then we prefer to indicate a "noise temperature" in K rather than a noise figure. This background noise depends much on how visible our warm Earth is for the antenna. This explains why UHF TV antennas better point slightly upwards, to remove some Earth from their main lobe while losing little signal near the maximum. More importantly, dishes for satellite TV have their primary source below the dish's axis to point strongly upwards, so the part of the primary's radiation that misses the dish aims at the sky rather than Earth. More refined low-noise antennas exist that minimize the secondary lobes of the primary source - but absorption by some material at 300K isn't an option, only reflection injects no reception noise.

With two op amp stages, the non-inverting first stage can use low resistances, since the output provides abundant current. This reduces the voltage noise, and at this location the current noise is unimportant. Differential instrumentation amplifiers with low voltage noise, typically meant to amplify thermocouple signal, use resistor values under 100ohm for that reason.

Hi JC, the source's internal impedance shorts the amplifier's input impedance.

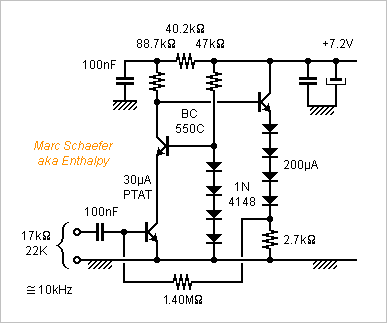
This slightly unusual circuit combines low noise with constant gain from discrete bipolars. The first stage amplifies voltages by 100. It's cascoded because I believed a big G22 in a datasheet. The follower brings only 0.8 voltage gain. Stability is uncertain at some source impedances. A capacitor at the cascode's output, or the general input, or very few pF across the feedback resistor would help. The junctions at the follower increase at heat the voltage drop across the cascode's load. With 7.2V supply, the current is proportional to the absolute temperature, and the transconductance and voltage gain constant. It's more a gadget here, but fun. Voltage regulators use to be extremely noisy, like 100nV/sqrt(Hz). The capacitor and split resistor at the cascode's load bring some 45dB @10kHz, power supply rejection by the closed loop does the rest. The second and third transistors add very little noise, which results essentially from the lone first transistor, advantage over an IC. At 10kHz and reasonably higher, it corresponds to Ic=30µA, Ib=10nA and 170ohm base spread resistance. The cascode's load resistor and the feedback add a bit. For 17.1kohm synthesized resistance, I find 4.5nV/sqrt(Hz) in open circuit, while a physical resistor would have 16.5nV/sqrt(Hz). At room temperature, the circuit is as quiet as a resistor at 22K. The emitter of the follower can provide an amplified output, to measure the circuit's impedance and noise, alone or connected to a similar one or a physical resistor. Marc Schaefer, aka Enthalpy

I would already have done it if I had my workshop here. Anybody should feel free to test it.

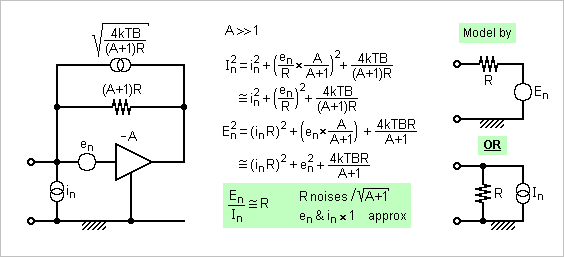
Indeed. I computed En and In from the open-circuit voltage and the short-circuit current. The setup can be modelled by a noise voltage or current source, not both, and a noiseless resistor R. The resistance and the noise voltage source give the short-circuit noise current and reciprocally. That's why I had found fully correlated noise and voltage sources. They were the same noise. So the setup doesn't double the amplifier's current and voltage noises, it just keeps them. Nice !

The Wiener oboe is still played, but essentially at the Wiener Philharmoniker, so it is uncommon wikipedia its fingerings differ from the usual conservatoire oboe and its bore is wider, producing a different sound. Hear it there JG86-Tm1ddY at 00:56 and hear the Wiener cor anglais there JG86-Tm1ddY at 01:25 The sound of the usual conservatoire oboe varies a lot among the instruments and oboists, nice example there 6m5zE9Eue9A softer because it's narrower. An oboe is not a cornet. More sounds by the conservatoire oboe family there yQ0ziInWbF4 jump there to the oboe, oboe d'amore and cor anglais; yQ0ziInWbF4 at 1:58 and 5:46 and 6:33 and 7:22 yQ0ziInWbF4 at 4:05 yQ0ziInWbF4 at 5:02 If you wonder, the language is Portuguese. From Portugal, with a rhythm very different from Brazil. And the oboe with unusual bell shape is from Dupin.

The bass flute is a tenor, one octave below the soprano, and is quite rare in symphonic music because it plays far too softly, but louder than the miniumm achievable on a saxophone. Amplification is mandatory. It also empties the flutist's lungs far too quickly. This one flutist gives the best demo I've found on the Web, jump to 6:07 here 0ogwt5yvmbw at 6:07 She achieves decent articulation by mere virtuosity, but the instrument has by nature a huge inertia, especially on low notes, and the score is chosen accordingly. I suppose the inertia results from the big tube fed by a small blowhole to fit human lungs. At organs, the low flute pipes articulate well. Already the alto flute, a fourth below the soprano, makes rarely sense at a symphonic orchestra in its huge hall. Fainter than a soprano, especially at low notes, and squanders breath even more. Same flutist and video, jump to 5:19 here 0ogwt5yvmbw at 5:19 and to other times to hear a piccolo or metal and wooden sopranos. By the way, the wooden soprano must be the Yamaha; others sound much more like metal, so only a part of the sound results from the material. Even lower flutes are built. The musicians use to play one spicato note per breath, which sounds like a noise vaguely suggesting a note height, as the note has too little time to appear. I won't link examples of that. That's why I suggest to amplify the air throughput by some Venturi for low flutes, building them as recorders if necessary.

I'll put my time elsewhere.

No, they propose a contact and measure a DC current.

I wanted to recommend a current feedback op amp or a transconductance feedback op amp, which enable low resistance value in the feedback loop and have a internal polarization that make the transconductance independent of the temperature. Alas, the IC I've seen are noisy. The designers had other priorities. One can still design a bias current proportional to the absolute temperature (PTAT) for a discrete bipolar transistor. Then, the voltage gain is not badly defined, and the noise minimum. A low resistance value increases the noise current In2 = 4kTB/R so there is an optimum in the impedances giving a minimum noise. We have little choice in the RF impedances. Too high, and stray capacitances limit the speed. Too low, stray inductances do. Around 50-100ohm, the impedance of usual printed lines, both stray capacitances and inductance act the same, and with proper design they add a constant propagation delay instead of slowing down the frequency response. Departing from the best impedances is avoided wherever possible. It was necessary for high-power RF amplifiers using bipolars because the transit time limits the epitaxy's thickness hence the breakdown voltage and the supply voltage. MOS do that better for being fast and allowing higher voltages, so the load impedance can be less low. But you still see very broad striplines in power amplifiers, and difficult emitter or source grounding.

Hi JC, thanks for your interest! With op amps, I'd use two of them (hence beware the stability). The first non-inverting, so its feedback doesn't load the input at all, the second inverting. Using at the first stage an amplifier stable on capacitive loads, you can have a mainly capacitive feedback divider that adds no noise. Such amplifiers are common within IC to make switched capacitor filters. After significant gain at the first stage, the noise of the second stage matters little. Though, I'd rather consider a lone bipolar transistor in common emitter as the amplifier. With ideality factor =1, the voltage gain is just the voltage drop in the load resistor divided by 26mW, so some bias help can stabilize the gain. A small resistor at the emitter would define the gain better. Other stages can reduce the output impedance.