-
Posts
3887 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by Enthalpy
-
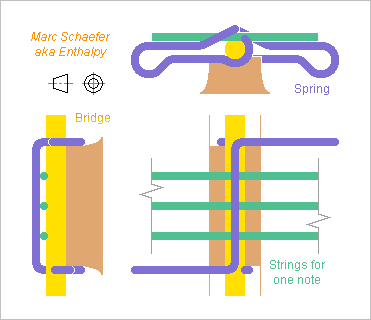
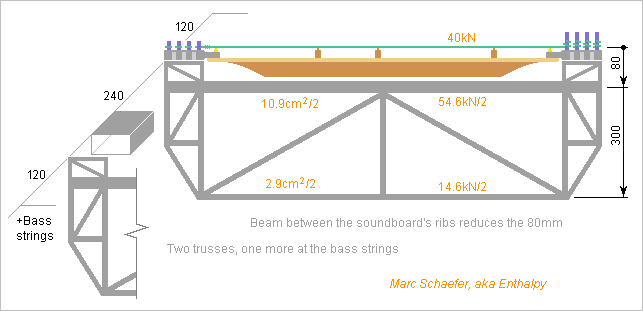
Manufacturer sites suggest that cimbalists rarely tune their 133 strings. A street musician can't often enough. But humidity and temperature let the wooden frame and soundboard detune the instrument. A metal frame shall stabilize the cimbalum's tuning, once its temperature matches the strings. Some manufacturers have steel or graphite between the wooden pinblocks, but metal everywhere would improve. Someone wanting the typical detuned cimbalom sound can still achieve it. So here it goes, and much applies to other instruments. ========== When humidity and temperature change the soundboard's stiffness, string passing the bridge straight keep their tension at the piano. Avoiding the push enables also a thinner, louder soundboard. The same at a cimbalom: Every second strand of strings arrives higher at the saddles and optionally the tuning pins and hitch (hanger) pins. The dampers, saddles, optionally pinblock must adapt to this. I happily leave this design to someone else. At most pianos' bridge, the strings make a zigzag around two inclined nails agraffes exist too, by phoenix phoenixpianos.co.uk and since the strands are spaced at the bridge of a cimbalom, dulcimer or zither (and this could apply to more instruments), we might pinch the strings delicately so they glide more easily: Spring manufactures bend spring wire to any shape, nonrecurring costs are reasonable. Many designs are possible, including one spring for many notes. The top shape must push on all strings. Here the ends centre the top on the bridge. One end hard to detach would prevent losing the spring. Springs give a force more predictable than screws or others. A layer of catalytic nickel loaded with Ptfe would ease the friction where possible, including at the saddles, but on the springs it's uneasy. When redesigning a cimbalom bridge, one might try strings of equal length within a note. At high notes, when the fundamentals of the short steel strings are in unison, different lengths prevent it for the partials, and possibly we perceive it. Pianos make this effort. ========== To match steel strings, I propose a frame of duplex stainless steel, but normal ferritic or martensitic steel, or cast iron, or austenitic stainless, would be decent to: scienceforums A grand cimbalom has 20 strands of 4 plain steel strings. I take D=0.7mm and D=0.8mm stretched to 1.1*C, or 1111MPa, so they cumulate 40kN roughly, spread over 0.48m. To simplify, I take uniform 0.8m from left to right pins, and the frame must preserve accurately the 4200µm string stretch. I can't estimate decently the bass strings. They will need some more frame, extrapolated from the plain steel strings section. Beams 80mm and 300mm below the strings receive 54.6kN and 14.6kN. 10.9cm2 and 2.9cm2 duplex there cumulate 8.8kg (more for the bass strings) and deform by 200µm, acting together 346µm on the strings. So tuning needs 3 passes after re-stringing, but in normal use, even if all strings had been a quartertone wrong, the first string drifts by 0.24% as all others get tuned, and this is inaudible to most people. The 50MPa stress doesn't determine the metal amount. If spread at two locations, 1/4 and 3/4 of the 0.48m, it leaves 5.5cm2 at the beams compressed by 27.3kN each. Even a 15mm*37mm plain section buckles at 32kN, and much more if supported laterally by skewed beams. Tubes reach more quickly the air temperature, but welded struts, cast parts, or a plate milled or laser-cut, are resistant enough. The pinblock of (duplex stainless) steel scienceforums can be welded on the beams and deforms little between the beams. If it's 80mm wide and keeps 2*140mm2 steel at the rims, EI=83000 SI, and over 4*0.12m with two support, 4*10kN bend it by 9µm only. 20mm thick plates would weigh 2*6.0kg but they can be cast or milled to leave steel just at the top, around the pins and at ribs between the pins, for maybe 2*2kg. Intuitively, limited torsion needs a closed section, obtained by welding plates or a truss. ========== The drawing shows strings at one single height, hiding complexity around the pinblocks. The soundboard holds at the metal frame but must be free enough to expand. Some flexible metal parts could contribute its movements, as on some Camac harps. This first attempt claims a metal frame is feasible, stable and light. Simpler and cheaper must be possible. Marc Schaefer, aka Enthalpy
-
Small corporate file servers, web servers, database servers and number crunchers are commonly built of few dozen blades holding each a pair of big recent expensive processors, with a rather loose network between the blades, and a Dram throughput that follows less and less the Cpu needs. I propose to use the better networks already described here and assemble more of used outfashioned cheap processors. This shall cumulate more throughput from the Dram, the network, optionally the disks. ========== Here I compare old and recent processors. All from Intel as they made most servers recently, but I have nothing against Amd, Arm and the others. I checked few among the 1001 variants and picked subjectively some for the table. North- and southbridges are soldered on existing mobos, hence not available second-hand nor usable, and new ones should remain expensive when outfashioned. So I checked only Cpu that directly access the Dram and create many Pci-E links to make the network. Chips on Pci-E links shall make ports for Ethernet and the disks like on add-on cards; I like Pci-E disks but they rob too much mobo area here. I didn't check what the Bios and monitoring need. One special card shall connect a screen, keyboard etc. I excluded Pci-E 2 Cpu for throughput and Pci-E 4 Cpu for price in 2019. Pci-E 3 offers 8GT/s per link and direction, so a good x16 network provides ~16GB/s to each Cpu. Line e is a desktop Cpu, less cheap. Lines f g are modern big Cpu that make a server expensive for a medium company. Lines a b c d are candidates for my proposal, in 2019 these have Avx-256 and Ddr3. None integrates a Gpu that draws 15W. | # GHz 64b | # MT/s | W | W/GHz | Cy/T | =========================================================== a | 4 2.8 (4) | 3 1333 | 80 | 7.1 (1.8) | 2.8 (11) | b | 6 2.9 (4) | 4 1600 | 130 | 7.5 (1.9) | 2.7 (11) | c | 8 2.4 (4) | 4 1600 | 95 | 4.9 (1.2) | 3.0 (12) | d | 6 2.4 (4) | 4 1600 | 60 | 4.2 (1.0) | 2.3 (9.0) | <<== =========================================================== e | 6 3.3 (4) | 4 2133 | 140 | 7.1 (1.8) | 2.3 (9.3) | =========================================================== f | 72 1.5 (8) | 6 2400 | 245 | 2.3 (0.3) | 7.5 (60) | g | 24 2.7 (8) | 6 2933 | 205 | 3.2 (0.4) | 3.7 (30) | =================================================================== a = Sandy Bridge-EN Xeon E5-1410. LGA1356, DDR3, 24 lanes, 20€. b = Sandy Bridge-EP Xeon E5-2667. LGA2011, DDR3, 40 lanes, 40€. c = Sandy Bridge-EP Xeon E5-4640. LGA2011, DDR3, 40 lanes, 50€. d = Ivy Bridge-EP Xeon E5-2630L v2. LGA2011, DDR3, 40 lanes, 40€. =================================================================== e = Haswell-E Core i7-5820K. LGA2011-3, DDR4, 28 lanes, 130€. =================================================================== f = Nights Landing Xeon Phi 7290. LGA3647, DDR4, 36 lanes, ++++€ g = Cascade Lake-W Xeon W-3265. LGA3647, DDR4, 64 lanes, 3000€ =================================================================== First # is the number of cores, GHz the base clock, 64b is 4 for Avx-256 and 8 for Avx-512. Next # is the number of Dram channels, MT/s how many 64b words a channel transfers in a µs. W is the maximum design consumption of a socket, called TDP by Intel. W/GHz deduces an energy per scalar or (Simd) computation. It neglects the small gains in cycle efficiency of newer Core architectures. Cy/T compares the Cpu and Dram throughputs in scalar and (Simd) mode, ouch! It's the number of cycles the cores shall wait to obtain one 64b or (Avx) word from the Dram running ideally. The price is for second hand, observed on eBay for reasonable bargains on small amounts in 2019. While an OS runs well from cache memory, most scientific programmes demand Dram throughput or are difficult to write for a cache. For databases, the Dram latency decides and it didn't improve for years. An Dram easy to use would read two data and write one per core and cycle, or Cy/T=0.33, which no present computer achieves. I favoured this ratio when picking the list. More cores make recent Cpu worse, wider Simd even worse. Assembling many old Cpu cumulates more Dram channels. Process shrinks improve the consumption per computation. If an oldfashioned Cpu draws 60W and a recent one saves the half by finishing faster, over 1/3 activity and 5 years the gain is 438kWh <100€, which doesn't buy a fashionable Cpu. If the Dram stalls the recent Cpu more often, the gain vanishes. ========== Each Cpu with its Dram, Ethernet and disk ports shall fit on a daughter board plugged by Pci-E x16 (or two x16 if any possible) on a big mobo that makes the network. But if Pci-E 3 signals can cross a Ddr4 connector, then carry 32+ lanes. The network comprises 16 independent planes where chips make a full crossbar, or if needed a multidimensional crossbar. Can a Cpu on the mobo make a 40*40 crossbar? It takes many Cpu there, and software makes slow communications. At least one crossbar Asic exists for Pci-E connections among Cpu. If that Asic isn't available, make an other. A 32*32 full matrix chip fits in a Dram chip package and can connect 1024 Cpu in a 2D crossbar. 15*16=240 Cpu and 8+8 lanes each take (15*16)*8=248 matrix chips. A chip can serve several smaller planes. The routing density needs a mobo with many layers. Repeaters may be necessary. A big machine with 480 Cpu connects any two Cpu in two hops and transfers 2TB/s through any equator in any direction. Better than a few fibres as a hypertorus. Many small Cpu outperform again few big ones. ========== Liquid cooling takes few mm over the Cpu. Some alkanes are insulators, good coolants, and hard to light Low-freezing rocket fuels New Dram chips soldered directly on the daughter boards, like on graphics cards, would enable 12.7mm spacing. Few 10€ pay 16GB presently. Used Dram modules would be bigger and more flexible, tilted connectors exist for Ddr4 at least au.rs-online.com and horizontal connectors for So-dimm. Or have a minimum Pcb to hold a second Dimm connector making the angle. Daughter boards need local regulators for the Cpu, Dram etc. Like graphics cards do, they can receive 12V from (many) Pc power supplies with minimum recabling. As the cabinet's sides are usefully reserved to Ethernet, the Sata disks and power supplies could reside in the doors. Using an Ivy Bridge-EP Xeon E5-2630L v2 or similar, each daughter board might sell for 250€. A small cabinet with 30 daughter boards would sell for 10k€, cumulate 3.5TFlops on doubles, Dram 1.5TB/s, network 240GB/s through the Equator. A big cabinet with 480 daughter boards would sell for 160k€. 56TFlops, 240TB/s, 1.9TB/s. 400MB/s disks, one per board, would cumulate 190GB/s. Drawings may come. Perhaps. ========== While not a competitor for the clean-sheet architectures I proposed previously, such machines assemble existing hardware. As Pci-E is fully compatible, the number and nature of the daughter boards can evolve, the size of the mobo too, and the boards can serve in successive machines at different customers. As they depend on available second-hand processors, the daughter boards would be diverse within a machine, and the software must cope with small variations in the instruction set. With reasonable capital, a startup company can buy used Cpu on eBay-Alibaba-etc, or rather complete old-fashioned servers with Dram and Ssd, and reorganize more components better around the superior network. Marc Schaefer, aka Enthalpy
-
And a (not favourable) opinion about a plastic trombone, with sound SITNi-5uVR0 it sounds terrible even with the metal mouthpiece. The musician gives more reasons against the instrument.
-
More opportunities to hear the baroque trumpet, played by Justin Bland here, wow: rRC1uN7r1mI and oeX8P0cqbUc on Youtube The modern trumpet can't imitate this sound desired by the composer and desirable. Incentive to build the semibaroque trumpet.
-
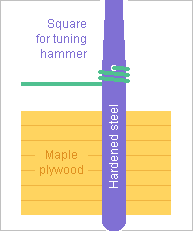
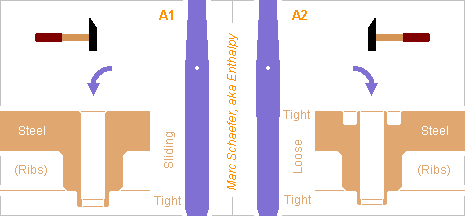
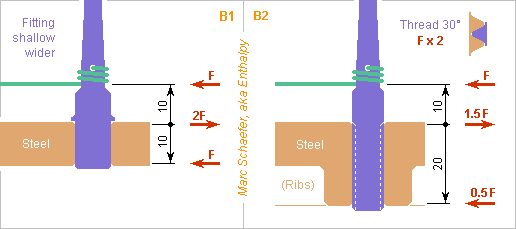
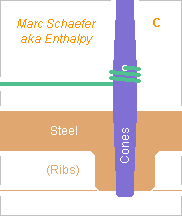
At instruments with many strings, the tuning pins and wrestplank (or pinblock) are uneasy to design, due to the big force, the many tuning pins fitting in limited space and budget, the quest for easy and stable tuning. At hitch pins (or hanger pins), the design without tuning is easier. Usually as depicted below, cylindrical accurate steel tuning pins hold by force in tight holes in a wooden wrest plank. Wood provides strong friction and, thanks to its elasticity, it demands a lesser accuracy in the hole tightness. Pins are of hardened steel at most zithers, dulcimers and cimbaloms but a nickel layer would prevent corrosion and bring smooth strong friction as at many pianos; maybe nickel adheres better on medium-carbon steel like 30CrMoV9 tempered at 500°C for hardness. At an example cimbalom, a D=0.8mm string that propagates at 1.3*C pulls almost 800N, and if it leaves the pin just 10mm above a stiff wrestplank, the bending moment is 8N*m. This induces 380MPa in a D=6mm pin, and wood's elasticity worsens the lever length. ========== If wood shall provide the pin 1600N friction from 0.4 coefficient on 25mm height, it needs 8MPa contact pressure at many close locations, too strong for the cross direction, demanding a plywood construction. Banal plywood may fail at hammered dulcimers; Steinway pianos have 7 plies of rock maple at 45° directions. Humidity and also heat let wood expand. Wood creeps also, letting the tuning drift within weeks and months at a new or restringed dulcimer. Here are suggestions for a steel pinblock that shall stabilize the tuning of steel strings. The steel isn't critical, it could be cast iron too, or match a frame steel for easier welding, or be duplex or austenitic stainless steel for best temperature stability of steel strings. Prior experience tells me that electroless nickel doesn't gall against stainless steel, but the pinblock may get electroless nickel too. On figure A1, the hole guides the pin on most height but a ring of metal holds it firmly. The stronger deformation is more easily adjusted. The coefficient of friction must be experimented. Taking 0.3 with nickel, 1600N friction result from elastic 300MPa in a h=2mm dR=1.4mm ring whose D=6mm is expanded by 9µm. Or plastic 550MPa in a h=1.5mm dR=1mm ring expanded by 0.1 to 0.3mm, but the initial force may drift due to creep. Reamers and grinding machines achieve the 9µm difference accurately. Reamers can be customized, here to several diameters. Without ribs, a customized milling tool guided by the hole can make the outer shape. A Cnc milling machine does it too and can leave ribs in the pinblock, and so does casting. The tight parts could have slits or other shapes that ease the deformations. I wouldn't use polymer nor elastomer rings as they creep badly, but separate metal parts could bring more elasticity, like coiled spring wire. They must hold without play at the pinblock. A second ring at the top would exclude dirt and guide even better the tuning pin, figure A2. On figure B1, the toppling moment creates 2*F+F on a shallow gliding fitting, so µ=0.3 would provide only 0.9*F, but the shaft widens. D=6mm to 9mm lets rub 1.35*F at the string, supposed to suffice even if µ=0.23. Maybe. On figure B2, the shaft and the pinblock have a thread whose 30° slope multiplies the rub force by 2 and diameter by 1.23, so 2*F with the deeper fitting and µ=0.3 bring 1.48*F at the string. On figure C, the tuning pin and the pinblock have fitting cones pressed in an other to rub enough. The user turns the pin as he presses, so little force suffices. Violinists do it with two fingers while holding the pegbox with the others, so the tuning hammer (=wrench) will suffice at a cimbalom or piano as it does at a harp. Reamers exist for the euronorm with dD/dh=0.02, but more slope might define the pin's height better. Rubbing 1600N at D=6mm H=25mm means some 11MPa compression or 57ppm deformation, so 12.6-10.7=1.9ppm/K mismatch between X2CrNiMoN22-5-3 and 30CrMoV9 change little over 10K variation. Or make the tuning pins of the same steel, cold-drawn if needed. Marc Schaefer, aka Enthalpy
-
Steel strings rust, slowly at a piano, faster at mallet instruments that play sometimes outside and are closer to the musician's hands, and more so at plucked instruments. While six strings are easily replaced, zithers and dulcimers can have 30 strands of 3 strings. But how stable can stainless strings be? Experiments shall decide. Stainless steel is abandoned at the piano; I suppose only austenitic steel was tried. Creep and losses may be worse than with carbon steel. All must be hardened by deep cold-work, but I don't have good data for this condition, so the following is unreliable. Martensitic stainless behaves much like carbon steel. Tempered below 300°C, the X20Cr13 stays tough and offers YTS>=1400MPa before cold-work improves it, as is expected but not documented. More alloying elements and less C, like Cr17Ni2Mo, resist corrosion better but offer less hardness and toughness. Variants of X20Cr13 with more carbon exist in some countries, others contain V and similar to form hardening carbides. Among them, X11CrNiMo12 (Böhler T552 and elsewhere) is a turbine alloy with known behaviour at 500-600°C, including creep. Cold-work and under-tempering aren't documented, logically. Tempered at 570°C and without cold work, it offers YTS>900MPa. Expansion 10.3ppm/K and E-modulus drift -174ppm/K (acting -87ppm/K on the frequency) suit a cast iron frame better than high-carbon steel does. Precipitation-hardening martensitic steels harden by ageing after easier cold-working and they resist corrosion far better than high carbon steel does. I have no modulus drift data about the Maraging Ni18Co12Mo5Ti (tough YTS~2360MPa without cold work) but expansion like 9.9ppm/K could fit cast iron. The stainless X3Cr13Ni8Mo2Al aka PH13-8 (Böhler N709 and elsewhere) offers tough YTS~1400MPa which cold work supposedly improves, expansion is 10.3ppm/K like carbon steel. The stainless PH15-7Mo becomes martensite by cold-work prior to ageing (YTS~1800MPa, can improve?), it expands by <9ppm/K to suit a cast iron frame better. Ledeburitic stainless resembles high-carbon steel. Hrc=57 to 60 as tempered nearly suffices, but can it be drawn, can wires be bent? Expansion 10.1ppm/K and E-modulus drift -174ppm/K for X90CrMoV18 suit a cast iron frame better than high-carbon steel does. Austenitic stainless harden by cold work and stay tougher than carbon steel. X12Cr17Ni7 achieves quickly 2000MPa and more, X2Cr17Ni12Mo2 needs deeper area reduction but resists finger corrosion better. Undrawn 15.6ppm/K would fit a frame of austenitic stainless steel or copper alloy. Precipitation-hardening austenitic steels expand even more: 16.2ppm/K for X5Ni26Cr15Ti, whose response to cold drawing isn't documented. Duplex stainless strings would excel against corrosion. YTS and toughness respond to cold reduction similarly to X12Cr17Ni7. 12.5ppm/K for X2CrNiMoN22-5-3 suggests a frame of duplex or austenitic stainless steel. CoCr20Ni16Mo7 resists corrosion better than all steels. It's known to exceed 2050MPa by cold-work plus ageing. 12.3ppm/K would match a duplex or austenitic frame. Nickel alloys for turbines are optimized against creep and known to harden by deformation. Expansion of 12.3ppm/K and E drift of -313ppm/K would let the alloy 718 fit an austenitic frame. Marc Schaefer, aka Enthalpy
-
What lets the tuning of a metal string drift? Humidity has no expected quick effect on steel. Creep acts very slowly at a piano, where margin below the proof strength might matter, knots quality too. Cold-drawn high-carbon steel expands by 10.4ppm/K. This compares with the string's stretch: 1111MPa/210GPa = 0.53% for 1.1*C. The sqrt drifts the frequency by -980ppm/K. Young's modulus drops by 300ppm/K or less: 210GPa to 205GPa from +20°C to +100°C, accelerates above. At constant length, the sqrt drifts the frequency by -150ppm/K. The change of the string's speaking length, for instance 12ppm/K, is negligible. The frame's expansion and deformation matters much. Stretching the string by 0.74% for 1.3*C reduces to -704ppm/K the thermal expansion effect. But if a string used at 0.8*C isn't overspun, the thermal expansion effect climbs to -1860ppm/K. The relative importance of Young's modulus drift goes the opposite way. Strings of cold-drawn titanium alloy, if practical, would expand less: 9.3ppm/K for Ti-Al6V4 vs 0.57% stretch at 1.1*C, while Young's modulus drops by 450ppm/K. Cold-drawn austenitic stainless steel seems to reduce its Young's modulus as quickly as carbon steel, but the X2CrNiMo17-12-2 expands by 16.2ppm/K (at least when annealed!) and the PH 15-7 Mo by 9ppm/K in condition RH950. Prior to cold-working, duplex X2CrNiMoN22-5-3 reduces its Young's modulus as quickly, but expands by 12.5ppm/K. Gut, polyamide and fluorocarbon polymers behave differently. ========== A perfect steel or cast iron frame expands by 10.4ppm/K too, leaving -150ppm/K due to the drift of Young's modulus. So if you tune at +20°C a cimbalom with hypothetic perfect steel frame and play it outdoors at +10°C, it goes sharp by 0.15%. Inaudible to most people, more so if all strings drift equally. In contrast, a wooden frame does drift, over temperature with some woods, and by humidity always. If the temperature changes by 2K in your room or concert hall, the piano with iron frame drifts by 0.03%, inaudible. ========== The strings' tension deforms the frame, whose Young's modulus drops with temperature too. So should its metal expand faster as a compensation? I don't believe so. The frame must deform far less than the strings to make the tunings independent. Also, the frame's deformation varies among the strings, so thermal expansion couldn't compensate it everywhere. Better a stiff frame whose expansion compensates only the strings. The frame is naturally bulkier than the strings anyway, and it must vibrate less, but its shape too must be stiff. ========== The frame can compensate the strings' Young's modulus drift too. At cold-drawn high-carbon steel stretched for 1.1*C, it acts as 0.15* the thermal expansion, so 12.0ppm/K at the frame would let play from 0°C to +40°C without the 0.3% frequency drift. For instance the stainless duplex X2CrNiMoN22-5-3 offers 12.5ppm/K, is strong and has nice fabrication capabilities. The martensitic X20Cr13 would be less perfect with 10.2ppm/K and the usual austenitic alloys less good with 15.8ppm/K. Aluminium expands more: AA2014 22.7ppm/K, AA5083 23.8ppm/K. 10K variation would detune steel strings by bad 1.1% and 2K by not good 0.2%. For Ti-Al6V4 strings too (harder alloys exist), a frame expansion of 11.9ppm/K would be good. That is, titanium strings could coexist with steel ones, overspun or not. Marc Schaefer, aka Enthalpy
-
More and more aeroplanes go electric, as the Beeb reports from Le Bourget bbc.com some claiming far better performance from battery-powered craft than my estimates here despite their wing isn't as wide. Hydrogen is missing in the report. Because of that, "electric" aeroplanes are said not to fly far, but the limit results from batteries. Hydrogen tanks and fuel cells give aeroplanes much more range than kerosene does.
-
Catalytic nickel protects against corrosion and is excellent against galling. I used some, with embedded Ptfe particles, at about 600MPa pressure and nearly no speed, against a martensitic stainless steel that galls horribly. The friction was tiny and very smooth without the stick-slip felt with zinc or phosphate layers against tempered steel. Embedded particles of MoS2 or graphite may be good too. Easy and smooth gliding would improve the bridges and saddles under the strings of some instruments. The piano uses steel nails to deflect the strings at the bridge. Wood receives already a gliding surface, the nails not, despite the force is bigger on them. Catalytic nickel with Ptfe should stabilize the tuning earlier. Some pianos have agraffes on the bridge instead. Same advantage. At least the cimbalum bends the strings over a metal rod at the many bridges. Easier gliding would equalize the tension among the sections between the bridges to improve the intonation. Especially important as the cimbalum has several strings per note. Many instruments have metal saddles or pins near the ends: harp, piano, cimbalom... where the deflection can be big. Better gliding would stabilize the tuning here too, just like violinists put graphite on the wood there. Tuning pegs would better rub smoothly too. They exist of hard wood or metal presently. At the violin, stick-slip of ebony pegs in the maple pegbox is a pain. But to replace ebony, nickel should rub strongly (no Ptfe), be black (graphite glides too easily), leave the fingers clean (embedded Ptfe doesn't). My gut feeling is that a hard polymer like LCP, possibly with a filler, has better chances than a metal. The piano, harp, cimbalom and others have metal tuning pins. Catalytic nickel protects against corrosion, rubs strongly without galling, and hopefully moves smoothly. Steinway pianos have already nickel-plated steel there. At string hooks, especially where piano strings make a U-turn without a knot, the strong friction of nickel might help tuning. Marc Schaefer, aka Enthalpy
-
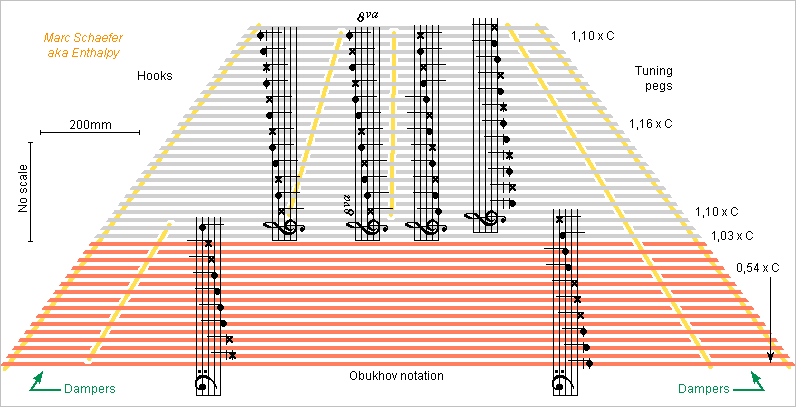
Here I propose a simpler notes chart for the cimbalom. The bass strands keep the usual positions up to B=234Hz, the rest differs: Semitones progress smoothly but for three jumps. At the jumps, the sections overlap by three semitones, similarly to trill keys at woodwinds. The sections have a constant interval. At the violin it helps. I imagine this chart makes the cimbalum easier to learn and play, but again I don't play it. Example of a usual (but incomplete) chart: beyondkarpaty.mutiny.net Hammered dulcimers would resemble more, but the intervals and bass strings differ. A pair of straight dampers can reach C=1051Hz while most Schunda-like models stop three semitones earlier. They are far from the struck positions. Schunda had achieved a nearly rectangular instrument shape at the cost of complicated notes chart and very inconsistent string sound speed even among consecutive notes. In my chart, the trapezoidal shape keeps the string sound speed between 1.10*C and 1.16*C at the treble and medium, varying very smoothly even at the section jumps, and decreasing gently to 0.54*C at the bass. Other string lengths would adjust these example figures, say between 1.20* and 1.27*. All bridges and saddles are straight on the drawing, but curves as at the piano could further equalize the string sound speed or limit the instrument's width. The outer bridges leave 10% non-speaking length in the corresponding strings, less than at a piano, but this can increase if accepting a slower propagation, at all these notes or only the lowest ones. Schunda's design has 39 strands, my chart has 43 with fewer spun strings. I suppose three strings per strand suffice. Marc Schaefer, aka Enthalpy
-
And oops. All pictures show one hook and one knot per string. Bad reason.
-
Here's a sketch of a big cimbalum that widens enough at the near strings to keep a good tension in the medium register, as suggested here yesterday. Its slope resembles much a small cimbalom. I fully ignore whether a wider instrument is difficult to play. If it helps to play near the centerline, the strings' tilt can be kept using taller bridges. For nicer and more uniform timbre, sound is here consistently 1.22* to 1.35* as fast in the medium strings as in the air. It remains faster than in air in half of the bass strings, whose plain steel saves money, then decreases in the spun strings to 0.58* at the lowest note. I'd keep the mass of the strings, that is, thinner if longer. Less stress is also welcome at the bigger frame. I've kept the distance from the bass bridges to the outer rails. Bringing less stiffness, strings passing the bridges straight might let shorten this distance. It is very short at a piano. Thanks to its metal frame, the piano also extends its soundboard very far under the agraffes and tuning pegs: to be copied if possible. Marc Schaefer, aka Enthalpy
-
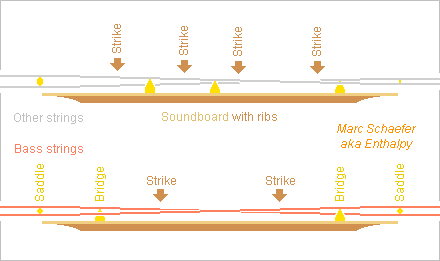
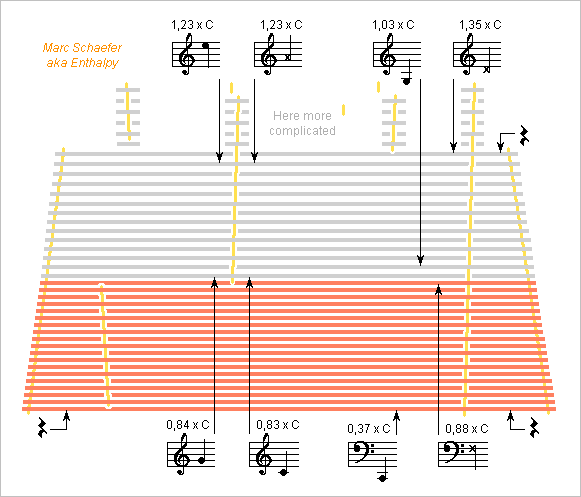
Here are some thoughts about the cimbalom. en.wiki - fr.wiki - cimbalombohak.sk - cimbalom.hu Big warning: I don't play the cimbalom nor any related instrument, so much here is probably b**ocks. If at the end one detail or an other makes sense, fine. Many instruments are called cimbalom, the name varies also much, and other instruments can be very similar. I consider the grand cimbalom, of Hungarian style, developed by Schunda around 1870. ========== If I see properly, the two sets of dampers are pushed down directly by long beams, possibly less stiff than needed. Hoping to make settings easier and more stable, I suggest: Individual movements for the dampers hold at a fixed beam; Individual springs to push each damper against a string course; One common action on each side, moved by the pedal, to pull all dampers from the strings; Optionally, the contact between the action and the dampers can be adjusted individually. The dampers for the central portions of treble strings still need some transmission. I wish the strings would sound for longer with the dampers. Enabling fine adjustments must help. ========== The medium alternates long string courses with others split in two by a bridge (bridges have voids for the uninterrupted strings). Angles by the bridges put courses higher at one end or the other to help the musician hit the desired note. If no bridge shortened these longer courses, an identical ratio between the full length, the longer part and the shorter part would be the golden number, (1+sqrt(5))/2 ~ 1.618. At identical sound speed in the strings, the intervals would be 8 or better 9 semitones (minor or major sixth) between full length, long part and short part, so 2*9 courses would span 27 semitones at uniform sound speed. The bridge loses about 2 semitones. That's still 4 semitones more than presently, with notes arranged more logically and with uniform sound speed. Whether this is advantageous, and enough so to learn a new string chart? ========== Why 4 strings per note? For a strong attack but longer sustain at medium and treble notes, 2 strings offer eigenmodes with no net force on the bridge and soundboard, and 3 strings suppress the roll moments too. 4 bring no further advantage here, and the piano has only 3. String inharmonicity improves with finer strings, and then more strings keep some moving mass. Though, I believe inharmonicity has been hugely overstated; it's not even a drawback with reasonable diameters like here. Maybe 4 strings cost less than 3. They replace a time-consuming knot on the instrument's left by a turn, plus one cheap tuning peg and its hole at the right. Pianos share some wires before and beyond the turn among adjacent notes, but their tension is very nearly the same, as opposed to the cimbalom. I suppose there is some design flexibility here. ========== Existing instruments widen very slowly at the low notes. Did Schunda consider his design already bulky and heavy enough? Consequently, the nearer strings are far too short, see the drawing: the farther medium strings are healthy 1.23*C or even 1.35*C long (as compared to the sound speed in air) but the nearer medium strings drop to 1.03*C or 0.83*C, and the nearer bass strings to meager 0.37*C, usually a receipe for bad sound. Small cimbaloms widen much more strongly at the nearer strings. Would it hamper playing the big instruments? At least, longer near strings would keep a decent sound speed. The farther medium strings could keep their length and the nearer be 1.3* as long. With the present notes chart, the nearer medium strings would be 1.08*C and 1.32*C long, perfect for plain steel strings and for the transition to spun bass strings. If keeping straight bridges, the lowest bass string would be 1.63* longer, or more decent 0.60*C. Drawing later and maybe. The instrument then widens from 1.5m to 2.1m. Many cimbaloms still have a wooden frame. I hope a metal frame would stabilize the tuning and let the instrument weigh less than Schunda's 1870 design, 100kg. Later and maybe. ========== The angles in the strings hamper the movements of the bridges and put also much pressure on the soundboard, which must be sturdy and is even supported by pillars under the bridges. Efficient reasons for the lack of sonority. Zig-zags at the bridge, like at the piano, would solve all. They are not possible at the highest strings. Elsewhere, they need an instrument higher at the sides, which a metal frame should enable. Later and maybe. Marc Schaefer, aka Enthalpy
-
From fresh pixel counting on grand pianos pictures, their treble and medium strings propagate the sound 1.2* as fast as air. The factor drops smoothly at the bass, which are spun with copper as soon as the factor is 1. Hungarian style grand cimbaloms have some strings long as 1.2* air half-waves, for few notes even 1.35*, but this drops to 0.83* at some plain steel strings, and to meagre 0.37* at the lowest spun strings. The puzzling arrangement of the strings gives very different string lengths to neighbour notes, jumping from 0.83 to 1.35 and back within semitones. So if the factor 0.83 contributes to the sound of some cimbalom notes, an imitating grand piano could be lowered by 6 semitones from 1.2. Or by 7, a fifth, for easier transposition. The cimbalom has also 3 or 4 strings per note except the lowest ones. At a piano, their tunes must match exactly to sound good. At a cimbalom, which has usually a wooden frame and produces from most strands several notes separated by bridges, the perfect match must be rare and brief. Unmatched tunes in strands may contribute to the cimbalom sound with its typical lisp. The prepared grand piano can imitate this easily. And of course, use special hard hammer heads or mallets. Marc Schaefer, aka Enthalpy
-
Algebraic proof that H5=H7=0 for the waveform with H3=-135dBc, having 35 transitions and T=210, here on June 01, 2019 Waveform ----------------------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + - + - + Positions | 0 5 6 9 12 14 17 25 27 31 33 36 37 42 43 50 51 52 | -5 -6 -9 -12 -14 -17 -25 -27 -31 -33 -36 -37 -42 -43 -50 -51 -52 ----------------------------------------------------------------------------------------- Harmonic 5 ----------------------------------------------------------------------------------------- Modulo T/5=42 | 0 5 6 9 12 14 17 25 27 31 33 36 37 0 1 8 9 10 | 37 36 33 30 28 25 17 15 11 9 6 5 0 41 34 33 32 ----------------------------------------------------------------------------------------- +21 if -Dirac | 21 5 27 9 33 14 38 25 6 31 12 36 16 0 22 8 30 10 | 37 15 33 9 28 4 17 36 11 30 6 26 0 20 34 12 32 ----------------------------------------------------------------------------------------- Ordered | 0 0 4 5 6 6 8 9 9 10 11 12 12 14 15 16 17 20 | 21 22 25 26 27 28 30 30 31 32 33 33 34 36 36 37 38 ----------------------------------------------------------------------------------------- Cycles | (0 14 28) (6 20 34) (8 22 36) | (0 21) (4 25) (5 26) (6 27) (9 30) | (9 30) (10 31) (11 32) (12 33) (12 33) | (15 36) (16 37) (17 38) ----------------------------------------------------------------------------------------- Harmonic 7 ----------------------------------------------------------------------------------------- Modulo T/7=30 | 0 5 6 9 12 14 17 25 27 1 3 6 7 12 13 20 21 22 | 25 24 21 18 16 13 5 3 29 27 24 23 18 17 10 9 8 ----------------------------------------------------------------------------------------- +15 if -Dirac | 15 5 21 9 27 14 2 25 12 1 18 6 22 12 28 20 6 22 | 25 9 21 3 16 28 5 18 29 12 24 8 18 2 10 24 8 ----------------------------------------------------------------------------------------- Ordered | 1 2 2 3 5 5 6 6 8 8 9 9 10 12 12 12 14 15 | 16 18 18 18 20 21 21 22 22 24 24 25 25 27 28 28 29 ----------------------------------------------------------------------------------------- Cycles | (2 12 22) (2 12 22) (5 15 25) | (8 18 28) (8 18 28) | (1 16) (3 18) (5 20) (6 21) (6 21) | (9 24) (9 24) (10 25) (12 27) (14 29) ----------------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy
-
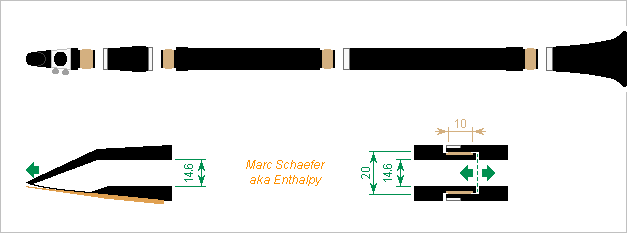
Most woodwind have corks where the joints fit in an other, and corks let woodwind bodies vibrate lengthwise. I take E=G=6MPa and losses=2.2% @1kHz for cork amorimcorkcomposites.com unexpected small losses, but cork does rebound, more so than many elastomers. ========== Let's take a soprano clarinet as an example, with D=14.6mm bore taken as uniform. At the mouthpiece, 1Pa creates 0.17mN axial force. At the fittings, the oscillating air pressure acts on Do~20mm Di=14.6mm to create forces as strong. The bell's flare too experiences axial forces. It the corks are 10mm long and 3mm thick (I have no clarinet at hand), their axial stiffness is 1.3MN/m. This resonates a 20g mouthpiece around 1.2kHz, and together with a 30g barrel at 0.8kHz. The bell resonates somewhat lower, and the driving force can originate elsewhere. If the upper and lower joints weigh 0.15kg each, their fitting resonates them around 0.6kHz. Or rather, these resonances combine. The joints, especially the bell, add their own lengthwise resonances. The frequencies reside at the fundamental's lower clarion to the upper registers, and at the strongest harmonics of the chalumeau register. Bad luck. 1Pa and 0.17mN would move the parts by 0.13nm in quadrature, but Q=45 resonances amplify this to 6nm in-phase. Facings create a lossy pulsation of 10-12m3. Compare with the air column: 1/2* 0.25m D=14.6mm make 21cm3 where 1Pa induce 1.5*10-10m3. A clarinet has Q>100 at these registers, so the lossy pulsation is 1.5*10-12m3. Corks create much losses at a clarinet, according to this model - but experiments decide as usual. It would be worse at an oboe or a bassoon, where the bore is a smaller fraction of the wood section. Q=45 lets affect one note and the neighbour semitones for being so strong. The resonance is too wide to conceal it between two notes, cork is too variable too. Not only is power lost. The blowing resistance is smaller, and the emission of the upper register may become harder. ========== A century ago, woodwinds had impregnated thread coiled on the tenons and bocals. Did it resonate less strongly? I didn't compare when I let install corks at my bassoon, alas. Many elastomers resonate less than cork does. Perfluoroelastomers are an extreme case, they are also hydrophobic and they glide well. Others are easier to glue and cheaper. A limit is that damping materials creep, so the fitting eases over time. ========== Some wooden flutes have silver tenons to connect the joints, for instance Yamaha's YFL-874W and YFL-894W europe.yamaha.com I had suggested that these tenons dampen the flexural resonances, here on Apr 01, 2019 they look also excellent to dampen the lengthwise resonances at the fittings of all wind instruments, since silver absorbs vibrations and is also stiffer than cork: 150MN/m for D=14.6mm e=0.35mm L=10mm. I take a perfectly stiff contact between the metal rings. On metal flutes, the bare accurate adjustment is airtight and slides gently, thanks to thin metal. I suppose that metal tenons in wooden flutes have a location where the diameter doesn't follow the deformations of wood. Maybe ebonite is stable enough that mouthpieces don't need an inner metal lining and the manufacturers don't learn new materials and fabrication methods. But the luthiers and workshops not used to flutes would have to learn adjusting metal rings. Besides (sterling) silver, PCM is a good instrument alloy, and some Ni+Co alloys are known dampers that can be electroformed too: easier for pure oboe or bassoon luthiers. More here on Nov 04, 2018 At a flute B-joint, the fitting is already much shorter than what a clarinet, oboe or bassoon needs. At a conical bore, the fitting must be cylindrical, hence a bit wider that the cone upwards and narrower downwards. Thin metal needs less wood thickness than cork and keeps more sturdy joints. When a clarinettist tunes his instrument down, this creates presently cavities at the air column with deep corrugations. Metal fittings improve this. But the chamber of a saxophone has important functions, so a new design must keep it. Marc Schaefer, aka Enthalpy
-
35 transitions improve further the waveforms with T=210: -135dBc. H1 H3 H5 H7 H9 H11 H13 | T a b c d e f g h i j k l m n o p q ============================================================================================= 0.52 -126 nil nil -11 -6 -8 | 210 2 7 8 10 12 14 15 16 19 27 28 31 33 40 42 50 51 0.47 -135 nil nil -28 -4 -8 | 210 5 6 9 12 14 17 25 27 31 33 36 37 42 43 50 51 52 ============================================================================================= T=140 and 180 with 35 transitions aren't quite as good as T=210. Neither did 15 transitions provide good waveforms with T<=702, T=840 nor T=1050. Marc Schaefer, aka Enthalpy
-
I had suggested an instruction copied from the Vax 11 's Subtract One and Branch, on 26 October 2015 and the 86 family has already one. ========== One computation I have quite often in my programmes is if (|x-ref| < epsilon) The operation on floating numbers is lighter and faster than a multiplication, hence easily done in one cycle. It's often in inner loops of heavy computations. Processors that don't provide this operation should. Depending on hardware timing, the instruction set could provide variants, preferibly the most integrated one: |x-ref| Compare |x-ref| with epsilon Branch if |x-ref| < epsilon Simd processors (Sse, Avx...) could compute on each component and group the comparisons by a logical operation, possibly with a mask, in the same instruction or a following one. Inevitably with Simd, it makes many combinations. ========== An other computation frequent in scientific programmes is if (|x-ref|2 < epsilon) It looks about as heavy as a multiplication-accumulation, but denormalizations take more time. If it fits in a cycle, fine, with the comparison and the branch, better, but it's obviously not worth a slower cycle. Here too, Simd machines could group the comparisons by a logical operation. I feel the square less urgent than the previous absolute value, which can replace it often. Also, a test is often done on the sum of the squared components of the difference instead, and such a sum is also useful alone, without a test nor a branch. Marc Schaefer, aka Enthalpy
-
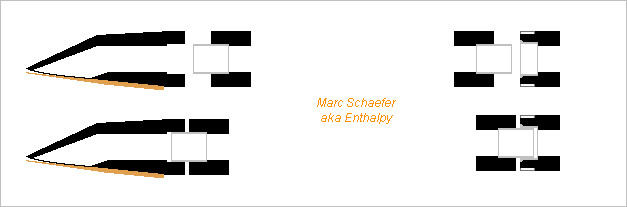
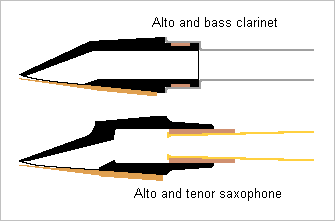
Hello everyone and everybody! I suggest to use the reed and mouthpiece from an alto or bass clarinet on an alto or tenor saxophone with a special bocal. The sound of a woodwind depends strongly on them, here it might resemble a tárogató. The bass clarinet and tenor saxophone can already swap the reed of similar size, but only a clarinet mouthpiece has a facing curve to match the clarinet reed's profile. The designs differ much. Not only is the clarinet facing's curve steeper at the tip, the bore is also much smoother. The bocal fits in the saxophone's mouthpiece but surrounds the clarinet's one, demanding a new bocal design. Proper intonation needs to tweak the evolution of the section at the new bocal and possibly put an insert in the mouthpiece. Corrugations may be necessary at the entrance to soften the sound, as the saxophone has much wider tone holes than a clarinet or a tárogató. I suggested to produce the bocal by metal deposition or graphite composite on Jan 01, 2018 - May 02, 2018 - Dec 04, 2018 Whether a saxophone can play pianissimo then? Marc Schaefer, aka Enthalpy
-
I suggested to replace spruce or sycamore with yew (Taxus baccata), here on February 10, 2019 12:33 AM, to increase the flexibility of the midrib of traditional harps while keeping the resistance. This applies to much of the harp's soundboard too. Wherever the strings' tension makes the soundboard too stiff, yew will be more flexible and louder. It would apply to any instrument whose strings tension limits the soundboard. How does yew sound in a harp? This must be experimented. Yew was sought after for mandolins, not only for long bows. The definitive way to build loud harps should be my soundboards parallel to the strings, which don't suffer the same limitations hence shouldn't benefit from yew. Marc Schaefer, aka Enthalpy
-
Hello dear friends! Here some thoughts and ramblings about an expert system seeking syntheses for organic compounds. ---------- Expert systems were among the first successful developments of artificial intelligence decades ago, well before machine learning https://en.wikipedia.org/wiki/Expert_system You can imagine them as a renunciation of the too complicated "if then else" control on the programmes by the programmer. Instead, the expert system comprises a knowledge base, that is a set of rules, possible actions applicable when their conditions are met, and an inference engine that has often zero knowledge of the topic but tries to apply billions of combinations of the rules to a situation proposed by the user. Expert systems are artificial intelligence in that sometimes they make "reasonings" far beyond what software is expected to, and in that the programmer doesn't try to predict their behaviour. Nice and successful ones existed for spectroscopy, geology, synthesis of digital circuits, and more. ---------- Seeking to produce a compound from more easily available reactants by applying reactions from a set of (at least here) known ones, organic synthesis resembles what an expert system can do. The case proposed by the user is the molecule to synthesize. The transformation rules are the the known reactions. Thousands exist, which is fine for an expert system. They have domains of validity, like the compatibility with other functions present on the intermediates: this is easy for expert systems. They are parameterized by some R, R', R"... parts of the compounds: nothing new for expert systems. Knowing the reactions in the reactants to products direction too can be useful, when the user asks "make this compound from this feed", which limits much the combinatorial explosion by starting the search from both ends. The system must know a set of reactants that tell "the retrosynthesis is finished". This is less usual, but easy to program. Perhaps as classes of reactants rather than individual ones, like "all 1-alkenes". As an interesting option, the system could first build from the known reactants a huge base of easily obtained intermediates, or classes of, that would short-circuit the time-consuming end of the retro-synthesis. Guides are necessary so the engine applies reactions towards ever simpler, or more easily obtained, intermediates. As these intermediates are not individually known, some sort of evaluation function must be very general, maybe by comparing some quick but fuzzy "distance" to the known reactants. This educated guess is not standard practice for expert systems. But allowing for a limited number of steps in a seemingly wrong direction is common practice. The combinatorial explosion is brutal in organic synthesis: thousands of known reactions, sometimes over 20 steps. The computer's brute force is the big argument of an expert system but it won't suffice by far. The evaluation function shall reduce the combinatorial explosion. Guidelines that indicate what reactions make probably more sense in a given situation may also help the inference engine. This is less common for expert systems, which tend to apply neutrally all possible rules. Some sort of "cost function" is necessary, not only to compare found syntheses, but also the guide the inference engine as it seeks syntheses. The function may consist of economic costs with al refinements (recurring, investment...) and include also the needs, desires, beliefs of the user, like "no poisons, no explosives" or "reactants from renewable sources" or "by-products easily disposed of" or "kg cost less important here". The cost function may compute more than a sum of the individual steps, for instance if no separation is needed between two reactions. Optional later refinement. ---------- This expert system seems bigger than the historical ones. Reorganizing digital circuits is simple in comparison with the application of thousands of reactions. The availability of vast chemical databases should help. The search for syntheses is naturally very parallel and can run on supercomputers. That's a detail, because artificial intelligence uses to succeed or fail by a factor of a zillion. Maybe the first thoughts should define a simpler first trial. One expected to provide encouraging results from a limited effort, even if it finds only very simple syntheses using few known reactions, as a proof-of-concept. Gentlemen, start your inference engines... Marc Schaefer, aka Enthalpy
-
Did I see such a circuit in Elektor or Radio Plans, to multiply the frequency of a reference transmitter? It was just after the last ice age, as the DCF77 antenna emerged from the melting shelf, so I don't remember quite accurately. Frequency *5 is perfectly reasonable with a transistor and a filter if you can adjust the resonant circuits, I did it a couple times. For series production, it demands serious precautions. Or individual tuning too. Nowadays, Pll and Dds are simpler, except for special needs. The standard way to get an accurate second is Gps. Horribly more complicated, but available ex stock. It resembles the electronic bubble level someone asked for elsewhere. He wanted to build the sensor, I suggested to put a webcam in front of a usual bubble level, plus image analysis software on a Pc. If you don't need to develop a webcam and a computer only for this, it can be considered. And, gasp!, the guy was happy to have a "simpler" solution than developing the sensor. Software has pretty much killed the fun in electrical engineering.
-
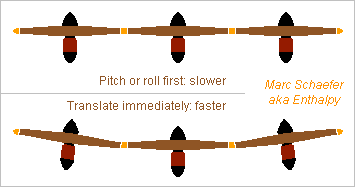
Multirotors use to have all rotors in the same plane. To translate longitudinally or sidewise, they must first pitch or roll, which takes time. The reaction time matters if flying in the wind near a moutain slope for instance, or near a building... I propose to tilt some or all rotors inwards, both length and sidewise. Increased thrust at some rotors and decreased at the opposite ones then creates immediately a net in-plane thrust and acceleration, even before the pitch or roll builds up. The tilt sketched here wastes 1% of the lift force for each tilt direction. Marc Schaefer, aka Enthalpy
-

Gravitational Interferometer and Kalman
Enthalpy replied to Enthalpy's topic in Astronomy and Cosmology
Light can cool at depth selectively. Still by photons that pick surrounding heat to achieve a transition of slightly bigger energy. The target transition could be introduced in the material's depth mainly. This can't be changed after manufacture. An improved version would introduce different transitions at varied depths, for instance colour centres that respond to different wavelengths. Varied light sources would cool different depths. Focussing the light at depth in a uniform material wouldn't cool more the focal plane, as the removed heat stays uniform after scanning. But a scheme where several photon absorptions produce the heat loss lets target a chosen depth of a uniform material. While two-photon absorption seems impractical, a multi-level absorption scheme, where for instance a first photon puts an electron on a higher energy level, from where a second photon puts the electron at an even higher energy with the help of heat, operates only where both beams illuminate the material. How to measure the heat profile? Maybe the comparison of Stokes and Antistokes does it - unclear to me: it's done for silicon at a high temperature. Rather, I suppose that the extinction coefficient of the cooling light tells the temperature. In itself a good thing, as light should cool the warmest locations faster, if the energy mismatch is well chosen. ========== Is cooling at selective depth interesting for the mirrors of a gravitational interferometer? I ignore that very accurately. But it looks interesting for thick optics, especially giant telescope mirrors and lenses that take a year to cool from the casting temperature. Are colour centres acceptable for them? Is their ceramic transparent enough? ========== The Kagra interferometer plans to cool mirrors down to 20K, but big optics must cool from the casting temperature, orange to dark red or near infrared. Thermal radiation is strong at these temperatures. Maybe well chosen dopants could be introduced at varied depths to emit more light at wavelengths that pass through the shallow material. Surrounding the material by mirrors that reflect or absorb specific wavelengths would then suffice to cool varied depths selectively. Marc Schaefer, aka Enthalpy -
Chains of frequency doublers, integrated on a chip, could be catalogue parts. To achieve frequencies above ~500MHz from a quartz or Saw resonator, Pll are more fashionable, but: Last time I searched for a prescaler at 40GHz, I didn't find any. Pll introduce phase noise, waste power and synchronize slowly on a new frequency. Frequency doublers pick the second harmonic from the nonlinear element with a frequency filter, usually narrowband and centred on each design's need. Careful design could make a larger passband and keep the rejection, especially with transmission zeros. The filter must pass the second harmonic and block the third and the fundamental, so the input frequency can't vary much. 1 to square root(2) ~1.414 input frequency band is (too) difficult: pass the second harmonic from 2.000 to 2.828 but block the third above 3.00, demanding 1.061 selectivity despite components tolerances and finite filtre steepness. 1 to cubic root(2) ~1.260 is reasonable: pass 2.000 to 2.520, block at 3.000 and beyond, selectivity 1.191. 1 to fourth root(2) ~1.189 is easier: pass to 2.378, block at 3.000, selectivity 1.261. A doubler chain chip would usefully expose the inputs and outputs of each stage, so the user chooses where his signal enters and leaves the chain according to the frequencies. The user then connects outside the chip the stages together, or sets control pins to do it internally and save buffer power. He may also shut down the unused stages. If the input frequency band is 1 to cubicroot(2), three catalogue chips cover all needs. [DoublerChain.png] A fast semiconductor, GaAs or more recent, can integrate the active and passive components up to 40GHz or 95GHz+ for instance. The passive components for the stages below few GHz reside better outside the chip, which can still provide the transistors. Alternately, a distinct chip can carry only wideband active components for a bunch of doublers and triplers, on a cheaper process like Cmos/Si. A hybrid circuit can carry passive components outside the chip and be still a catalogue part. On-chip or on-hydrid tuning would be useful if possible, at biasses to minimize the unwanted harmonics, and even better at the filters - not only for the present chain. The doubler circuit I proposed here on 03 December 2012 saves power and eases the harmonic filter. Expect more components at the selective wideband filter than the two resonating circuits I drew for the narrow passband. The tripler I proposed here on 18 May 2019 would be conceivable but it restricts the bandwidth even more, needing more catalogue chips to cover all frequencies, so I'd put some rather at an aperiodic (part of a) chip. One catalogue chip could also carry all the doubler chains needed to cover all input frequencies and let the user drop away and switch off the unecessary ones, through cabling or by setting control pins. Marc Schaefer, aka Enthalpy