Enthalpy

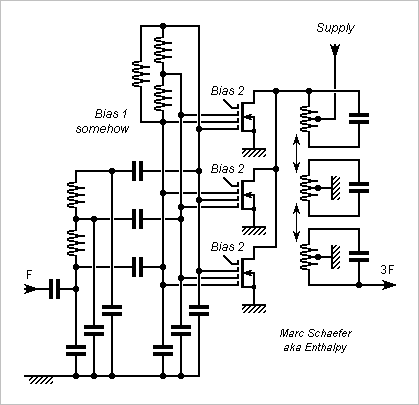
This frequency tripler starts like a distributed amplifier, with a circuit to provide signals 120° apart, and drives three nonlinear components whose outputs cumulate without phasing in a filter. This isn't uncommon, and attenuates the harmonics 1, 2, 4... when the third is wanted. Usual circuits would drive components, for instance bipolar transistors, to a strongly nonlinear amplitude. The small conduction angle lets the output current contain usable harmonics, in addition to the strong fundamental. Here I propose to use Fet with 3 or 4 gates connected to the three phases. Any gate can cut the drain current, which passe hence by zero three times per input period. This squeezes the fundamental amplitude in the drain current, and it also reduces the power consumption. The fourth gate is optional. It enables a smaller input power, and with the proper bias, it reduces the even harmonics. Three paired transistors, whose gates swap the input phases, symmetrize the output current, squeezing further the unwanted harmonics. I've drawn a three-phase ring resonator at the input, downstream the phaser. This one uses identical components and equalizes the amplitudes and phases that are sensitive to tolerances at the phaser. Additional ring resonators are possible. Two resonating circuits can suffice at the output, three are easier at a tripler because the filter must squeeze the fourth harmonic near the third. Traps would be sensible. The circuit could multiply the frequency by 5 with more transistors and gates, but the filters become uneasy and the output signal weak, as usual. For Hf, Vhf and Uhf, a Mos silicon chip could carry the three multigate transistors already connected, for use with an external filter. For microwaves, a chip of adequate semiconductor could integrate faster Fet and the passive components, as lumped constants, or at higher frequencies as microstrips and rings. Untested, but this one can only work. Marc Schaefer, aka Enthalpy

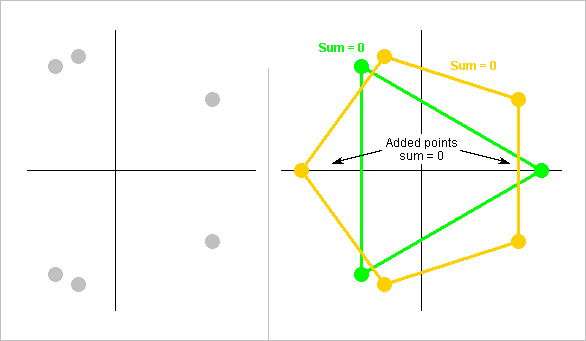
I suggested to add virtual points to a constellation to prove its sum is zero May 05, 2019 12:50 am It hasn't been necessary up to now, so here's an artificial case to illustrate it.

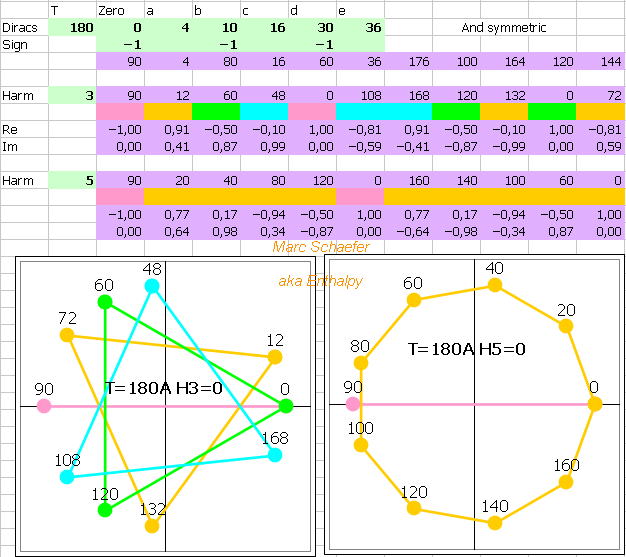
Algebraic proof that H5=H7=0 for the waveform with H3=-124dBc, having 33 transitions and T=210, from May 13, 2019 here Waveform ------------------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + - + - + - + Positions | 0 3 4 9 10 12 14 16 20 21 23 36 41 42 43 50 51 | -3 -4 -9 -10 -12 -14 -16 -20 -21 -23 -36 -41 -42 -43 -50 -51 ------------------------------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------------------------------- Modulo T/5=42 | 0 3 4 9 10 12 14 16 20 21 23 36 41 0 1 8 9 | 39 38 33 32 30 28 26 22 21 19 6 1 0 41 34 33 ------------------------------------------------------------------------------------- +21 if -Dirac | 0 24 4 30 10 33 14 37 20 0 23 15 41 21 1 29 9 | 18 38 12 32 9 28 5 22 0 19 27 1 21 41 13 33 ------------------------------------------------------------------------------------- Ordered | 0 0 0 1 1 4 5 9 9 10 12 13 14 15 18 19 20 | 21 21 22 23 24 27 28 29 30 32 33 33 37 38 41 41 ------------------------------------------------------------------------------------- Cycles | (0 14 28) (1 15 29) (4 18 32) (5 19 33) | (9 23 37) (10 24 38) (13 27 41) | (0 21) (0 21) (1 22) (9 30) (12 33) (20 41) ------------------------------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------------------------------- Modulo T/7=30 | 0 3 4 9 10 12 14 16 20 21 23 6 11 12 13 20 21 | 27 26 21 20 18 16 14 10 9 7 24 19 18 17 10 9 ------------------------------------------------------------------------------------- +15 if -Dirac | 0 18 4 24 10 27 14 1 20 6 23 21 11 27 13 5 21 | 12 26 6 20 3 16 29 10 24 7 9 19 3 17 25 9 ------------------------------------------------------------------------------------- Ordered | 0 1 3 3 4 5 6 6 7 9 9 10 10 11 12 13 14 | 16 17 18 19 20 20 21 21 23 24 24 25 26 27 27 29 ------------------------------------------------------------------------------------- Cycles | (0 10 20) (3 13 23) (7 17 27) | (1 16) (3 18) (4 19) (5 20) (6 21) (6 21) | (9 24) (9 24) (10 25) (11 26) (12 27) (14 29) ------------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy

33 transitions improve the waveforms with T=210. T=180 stays bad. The reduction in H3 to -124dBc is compatible with luck and a uniform distribution of the harmonic voltage amplitude. The many trials result from minor optimizations, overclocking, and patience. H1 H3 H5 H7 H9 H11 | T a b c d e f g h i j k l m n o p ==================================================================================== 0.48 -115 nil nil -10 -23 | 210 1 2 7 10 11 12 14 15 20 24 35 38 45 46 47 48 0.35 -124 nil nil +4 -12 | 210 3 4 9 10 12 14 16 20 21 23 36 41 42 43 50 51 ==================================================================================== An different attempt up to T=554 and at T=630 with 15 transitions was sterile. Marc Schaefer, aka Enthalpy

Algebraic proof that H5=H7=0 for some long waveforms listed on May 05, 2019 06:35 pm Since T=210 divides by 5 and 7, I don't multiply the Diracs' positions by 5 or 7 any more; instead, I keep them but compute modulo 42 or 30 respectively. ---------- Waveform (210, 2, 7, 14, 16, 19, 20, 26, 28, 42, 43) Waveform ------------------------------------------------------------- Dirac sign | + - + - + - + - + - + Positions | 0 2 7 14 16 19 20 26 28 42 43 | -2 -7 -14 -16 -19 -20 -26 -28 -42 -43 ------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------- Modulo T/5=42 | 0 2 7 14 16 19 20 26 28 0 1 | 40 35 28 26 23 22 16 14 0 41 ------------------------------------------------------------- +21 if -Dirac | 0 23 7 35 16 40 20 5 28 21 1 | 19 35 7 26 2 22 37 14 21 41 ------------------------------------------------------------- Ordered | 0 1 2 5 7 7 14 16 19 20 21 | 21 22 23 26 28 35 35 37 40 41 ------------------------------------------------------------- Cycles | (0 7 14 21 28 35) (7 21 35) | (1 22) (2 23) (5 26) | (16 37) (19 40) (20 41) ------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------- Modulo T/7=30 | 0 2 7 14 16 19 20 26 28 12 13 | 28 23 16 14 11 10 4 2 18 17 ------------------------------------------------------------- +15 if -Dirac | 0 17 7 29 16 4 20 11 28 27 13 | 13 23 1 14 26 10 19 2 3 17 ------------------------------------------------------------- Ordered | 0 1 2 3 4 7 10 11 13 13 14 | 16 17 17 19 20 23 26 27 28 29 ------------------------------------------------------------- Cycles | (0 10 20) (3 13 23) (7 17 27) | (1 16) (2 17) (4 19) | (11 26) (13 28) (14 29) ------------------------------------------------------------- ---------- Waveform (210, 1, 2, 4, 6, 10, 19, 25, 34, 35, 39, 41, 43, 46) Waveform ------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + Positions | 0 1 2 4 6 10 19 25 34 35 39 41 43 46 | -1 -2 -4 -6 -10 -19 -25 -34 -35 -39 -41 -43 -46 ------------------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------------------- Modulo T/5=42 | 0 1 2 4 6 10 19 25 34 35 39 41 1 4 | 41 40 38 36 32 23 17 8 7 3 1 41 38 ------------------------------------------------------------------------- +21 if -Dirac | 21 1 23 4 27 10 40 25 13 35 18 41 22 4 | 41 19 38 15 32 2 17 29 7 24 1 20 38 ------------------------------------------------------------------------- Ordered | 1 1 2 4 4 7 10 13 15 17 18 19 20 21 | 22 23 24 25 27 29 32 35 38 38 40 41 41 ------------------------------------------------------------------------- Cycles | (1 15 29) (4 18 32) (7 21 35) | (10 24 38) (13 27 41) | (1 22) (2 23) (4 25) | (17 38) (19 40) (20 41) ------------------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------------------- Modulo T/7=30 | 0 1 2 4 6 10 19 25 4 5 9 11 13 16 | 29 28 26 24 20 11 5 26 25 21 19 17 14 ------------------------------------------------------------------------- +15 if -Dirac | 15 1 17 4 21 10 4 25 19 5 24 11 28 16 | 29 13 26 9 20 26 5 11 25 6 19 2 14 ------------------------------------------------------------------------- Ordered | 1 2 4 4 5 5 6 9 10 11 11 13 14 15 | 16 17 19 19 20 21 24 25 25 26 26 28 29 ------------------------------------------------------------------------- Cycles | (1 6 11 16 21 26) (4 9 14 19 24 29) | (5 15 25) | (2 17) (4 19) (5 20) | (10 25) (11 26) (13 28) ------------------------------------------------------------------------- ---------- Waveform (210, 3, 4, 5, 6, 11, 14, 15, 17, 26, 27, 29, 31, 43, 45) Waveform ----------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + - + - + Positions | 0 3 4 5 6 11 14 15 17 26 27 29 31 43 45 | -3 -4 -5 -6 -11 -14 -15 -17 -26 -27 -29 -31 -43 -45 ----------------------------------------------------------------------------- Harmonic 5 ----------------------------------------------------------------------------- Modulo T/5=42 | 0 3 4 5 6 11 14 15 17 26 27 29 31 1 3 | 39 38 37 36 31 28 27 25 16 15 13 11 41 39 ----------------------------------------------------------------------------- +21 if -Dirac | 0 24 4 26 6 32 14 36 17 5 27 8 31 22 3 | 18 38 16 36 10 28 6 25 37 15 34 11 20 39 ----------------------------------------------------------------------------- Ordered | 0 3 4 5 6 6 8 10 11 14 15 16 17 18 20 | 22 24 25 26 27 28 31 32 34 36 36 37 38 39 ----------------------------------------------------------------------------- Cycles | (3 10 17 24 31 38) (4 11 18 25 32 39) | (0 14 28) (6 20 34) (8 22 36) | (5 26) (6 27) (15 36) (16 37) ----------------------------------------------------------------------------- Harmonic 7 ----------------------------------------------------------------------------- Modulo T/7=30 | 0 3 4 5 6 11 14 15 17 26 27 29 1 13 15 | 27 26 25 24 19 16 15 13 4 3 1 29 17 15 ----------------------------------------------------------------------------- +15 if -Dirac | 0 18 4 20 6 26 14 0 17 11 27 14 1 28 15 | 12 26 10 24 4 16 0 13 19 3 16 29 2 15 ----------------------------------------------------------------------------- Ordered | 0 0 0 1 2 3 4 4 6 10 11 12 13 14 14 | 15 15 16 16 17 18 19 20 24 26 26 27 28 29 ----------------------------------------------------------------------------- Cycles | (0 10 20) (4 14 24) (6 16 26) | (0 15) (0 15) (1 16) (2 17) (3 18) | (4 19) (11 26) (12 27) (13 28) (14 29) ----------------------------------------------------------------------------- ---------- Waveform (210, 2, 9, 18, 21, 22, 24, 28, 30, 32, 33, 38, 40, 43, 45, 51) Waveform --------------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + - + Positions | 0 2 9 18 21 22 24 28 30 32 33 38 40 43 45 51 | -2 -9 -18 -21 -22 -24 -28 -30 -32 -33 -38 -40 -43 -45 -51 --------------------------------------------------------------------------------- Harmonic 5 --------------------------------------------------------------------------------- Modulo T/5=42 | 0 2 9 18 21 22 24 28 30 32 33 38 40 1 3 9 | 40 33 24 21 20 18 14 12 10 9 4 2 41 39 33 --------------------------------------------------------------------------------- +21 if -Dirac | 21 2 30 18 0 22 3 28 9 32 12 38 19 1 24 9 | 40 12 24 0 20 39 14 33 10 30 4 23 41 18 33 --------------------------------------------------------------------------------- Ordered | 0 0 1 2 3 4 9 9 10 12 12 14 18 18 19 20 | 21 22 23 24 24 28 30 30 32 33 33 38 39 40 41 --------------------------------------------------------------------------------- Cycles | (0 14 28) (4 18 32) (10 24 38) | (0 21) (1 22) (2 23) (3 24) (9 30) (9 30) | (12 33) (12 33) (18 39) (19 40) (20 41) --------------------------------------------------------------------------------- Harmonic 7 --------------------------------------------------------------------------------- Modulo T/7=30 | 0 2 9 18 21 22 24 28 0 2 3 8 10 13 15 21 | 28 21 12 9 8 6 2 0 28 27 22 20 17 15 9 --------------------------------------------------------------------------------- +15 if -Dirac | 15 2 24 18 6 22 9 28 15 2 18 8 25 13 0 21 | 28 6 12 24 8 21 2 15 28 12 22 5 17 0 9 --------------------------------------------------------------------------------- Ordered | 0 0 2 2 2 5 6 6 8 8 9 9 12 12 13 15 | 15 15 17 18 18 21 21 22 22 24 24 25 28 28 28 --------------------------------------------------------------------------------- Cycles | (2 12 22) (2 12 22) (5 15 25) (8 18 28) (8 18 28) | (0 15) (0 15) (2 17) (6 21) | (6 21) (9 24) (9 24) (13 28) --------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy

Here's an algebraic proof that H3=H5=0 for the waveform (210, 3, 10, 15, 30, 32) of Jan 21, 2018 9:58 pm updated May 07, 2019 ------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + Positions | [ -32 -30 -15 -10 -3 0 ] 3 10 15 30 32 ------------------------------------------------------------------------- *3, +T/2 if - | 114 15 165 75 201 105 9 135 45 195 96 Increasing | 9 15 45 75 96 105 114 135 165 195 201 Cycles | (15 45 75 105 135 165 195) (96 201) (9 114) ------------------------------------------------------------------------- *5, +T/2 if - | 50 165 135 55 195 105 15 155 75 45 160 Increasing | 15 45 50 55 75 105 135 155 160 165 195 Cycles | (15 45 75 105 135 165 195) (50 155) (55 160) ------------------------------------------------------------------------- First cycles with 7 members. Marc Schaefer, aka Enthalpy

T was twice longer than needed on Jan 21, 2018 9:58 pm T=90 and T=210 allow H3=H5=0, so here's an aggiornamento: H1 H3 H5 H7 H9 H11 | T a b c d e ==================================================== 0.42 nil nil -2 2 -3 | 90 2 5 8 15 18 0.71 nil nil -9 -11 -3 | 90 4 9 10 15 16 0.79 nil nil -20 nil 1 | 210 3 10 15 30 32 ==================================================== H3=0 for the first time with T=210. More harmonics show that the second waveform outperforms the first one. The third suggests two matched resistors to squeeze H7. (210, 5, 14, 16) suggested already two matched resistors to squeeze H3 and H9 at once. Mar 04, 2018 9:05 pm

But no yellow fume from dry oak in chimneys. It is lead the cause. Presently in the lungs of people who breathed it. And on the clothes and walls, where it can still be removed.

Detail improvement let my dumb program Search2931357.zip find T=210 waveforms with 29 and 31 transitions per half-period. They increase the H1 amplitude or squeeze the H3 further, as compared with the waveforms of Mar 03, 2018 that make the top of the table here. H1 H3 H5 H7 H9 | T a b c d e f g h i j k l m n o ============================================================================ 0.73 -104 nil nil -23 | 210 2 7 14 16 19 20 26 28 42 43 0.34 -114 nil nil 6 | 210 3 6 7 14 22 35 36 38 43 45 46 0.59 -111 nil nil -19 | 210 5 6 10 14 16 17 19 20 29 32 44 46 0.38 -114 nil nil -8 | 210 1 2 4 6 10 19 25 34 35 39 41 43 46 ============================================================================ 0.61 -111 nil nil -19 | 210 3 4 5 6 11 14 15 17 26 27 29 31 43 45 0.42 -115 nil nil -9 | 210 1 2 4 9 16 19 24 26 29 31 35 36 41 43 51 0.30 -116 nil nil -6 | 210 2 9 18 21 22 24 28 30 32 33 38 40 43 45 51 ============================================================================ T=180 is bad but here T=210 improves a bit. Marc Schaefer, aka Enthalpy

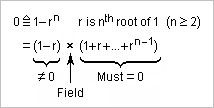
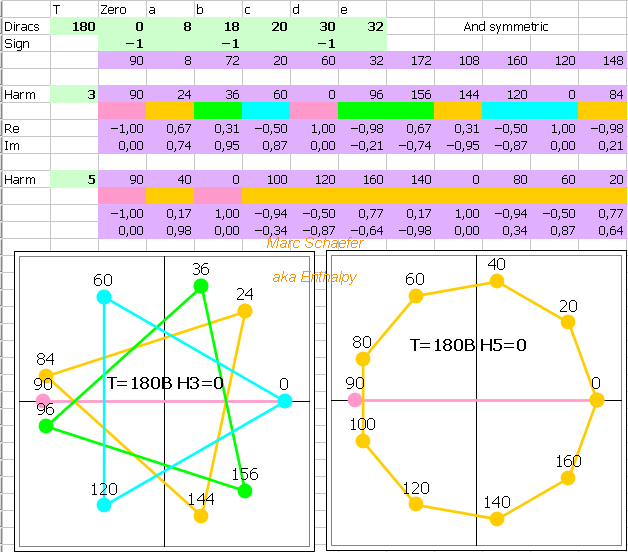
I forgot to explain in the last message that, when a Dirac is negative in the convolving sequence, and has the position p after multiplication by the harmonic rank, I replace it with a positive one at position T/2-p or T/2+p. The effect on the harmonic's amplitude is the same. Diracs all positive can then be grouped just by their spacings. ========== Here's a algebraic proof that H5=H7=0 in the (210, 5, 14, 16) sequence I proposed and depicted on Mar 04, 2018 9:05 pm and Mar 17, 2018 8:33 pm I multiply the positions by 5 respectively 7, replace the negative Diracs positions p by positive ones at T/2-p, compute modulo T=210, and sort by increasing positions: ================================ + - + - + - + H1 -16 -14 -5 0 5 14 16 ================================ H5 130 175 185 105 25 35 80 25 35 80 105 130 175 185 ================================ H7 98 203 175 105 35 7 112 7 35 98 105 112 175 203 ================================ Then I group the Diracs: H5 (25 130) (80 185) (35 105 175) H7 (7 112) (98 203) (35 105 175) The pairs are T/2=105 ticks apart, the triplets T/3=70, so the sums are zero. This very short sequence was manageable by looking at the numbers. The previous (180, 4, 10, 16, 30, 36) needed drawings. Sequences with 27 transitions need some better help. ========== The proofs explain why highly composite sequence lengths like 180 or 210 favour the suppression harmonics. They don't explain why the rank of a suppressed harmonic divides the length of the found sequences. Was it a coincidence? Marc Schaefer, aka Enthalpy

The cathedral's owner, that is the French government, was warned of the danger for an all-important monument, and got obvious recommendations. It didn't act. The catastrophe happened. You mean, it's less faulty because the government does it often? ========== The answer to early questions in the thread, "why was there no extinguishing system", is now known: carelessness. Prof. Vannucci also answers an other interrogation in this thread, whether water would do more harm than good. He proposed powder extinguishers. Definitely less harmful than a destruction. Even occasional malfunction is tolerable.

Here's eventually an algebraic proof that H3=H5=0 for both T=180 sequences with 11 transitions scienceforums on Jan 21, 2018 9:58 pm Of the convolving sequence explained there scienceforums on Jan 13, 2018 6:38 pm I represent the complex amplitude of a given harmonic, H3 or H5, at each position of a Dirac, including the ones before zero. These amplitudes are also the contributions of each Dirac to said harmonic, by Fourier series. The angles are computed modulo one turn, that is 180 ticks here. Then, I use the known property that in a (commutative?) field, here the complex numbers, the sum of the powers of a root of 1 is zero. On the diagrams above, I use n=3 and n=9. n=2 too if you decide that sqrt(1)=-1, or rather use 1-1=0. The 3rd and 9th roots of 1 are exp(j*2pi/3) and exp(j*2pi/9) in the complex plane. Any set of points regularly spaced on the unit circle has a null sum, including if all are multiplied by the same amount exp(j*angle). The positions of the Diracs in the sequance are multiplied by the harmonic's order, modulo one turn. I could decompose the constellations into sums of 2, 3 or 9 points regularly spaced. The set of 9 could also be 3 sets of 3. Spacing is 20, 60 and 90 ticks here, for 180 ticks per period, displayed as 40°, 120° and 180°. Note that these sequences occupy the point 1 twice. Because the convolving sequence is even, the imaginary part of all harmonics' amplitude is zero. Interesting is the real part of the sums. Conjugating some points may help to form regularly spaced sets. Here it wasn't necessary. Adding to a constellation virtual points whose sum is zero may help form several regularly spaced sets. Here it wasn't necessary. I ignore if all good convolving sequences must be constructed that way, and leave this question to a mathematician. Software searching only convolving sequences constructed that way may be faster than what I did, but programming is not trivial. Here is the spreadsheet. The original xml is for Gnumeric, the exported xls for Excel loses some formatting. ProofT180abH3H5.zip Marc Schaefer, aka Enthalpy

A report by prof. Paolo Vannucci told three years in advance that dust made Notre-Dame's attic highly flammable, that no extinguishing system was present, That the risk of fire was very high, and recommended to install some automatic extinguisher, optionally using powder. (Italian) ilsole24ore.com (French) marianne.net - liberation.fr The French government acted exactly as it uses to and is known to act: It didn't let remove the dust. It didn't let install an extinguishing system. But it made the report secret "because it could inspire terrorists". I wonder if communist Albania was as opaque and compulsory secretive as the French state is. And the result is here. The fire won't change the French state's habits. About lead oxide in the fumes, it acts presently exactly as it uses to. Oh, and Pascal Paillard, head of the Materials and Metals Department at Nante's Institute for Materials, also tells that the smoke was yellow due to lead oxide. The same colour was observed in the cathedral fires of Reims in 1914 and Chartres in 1836, which had lead roofings. More to come

Keep this lead preciously for science! More useful than making bronze of it. Explanations there: nature.com - scientificamerican.com - newatlas.com

Lead from the roof shouldn't be discarded as ordinary toxic waste. It's precious for science, as a shield material against ionizing rays. Freshly mined lead contains radioactive nuclides (elements and I suppose lead isotopes) from the parent nuclides that decayed into lead. They create background noise in the rays detectors. In old lead, most unstable nuclides have already disappeared. Some experiments used lead from sunken antique boats. Several 100t of Pb, 800 years old, is a fabulous asset for science.

I strongly disagree with the use of software to design an analog circuit. I used software to design analog chips, hand computation for macroscopic circuits, so I know both. Computing an analog circuit is generally trivial. I often do it without writing anything nor even drawing a diagram, cabling the breadboard directly while computing in my head, sometimes with a pocket calculator. My opinion is that anyone who needs software for that isn't able to design a circuit. The result would be bad, with or without software. What makes an analog design work isn't generally the diagram - unless the designer fails even there - but the good cabling, shielding, board design, for the electromagnetic compatibility. It's also a matter of proper component selection, knowing the detailed behaviour of each component technology. A simulation software helps zilch for that, which is the core difficulty of the job and takes most time. If a designer uses Spice to cope with the diagram, that suggests that he isn't even aware of all the other difficulties. Problems ahead. Engineering schools and universities replaced workbench time with simulation because it costs less, and because many teachers aren't even aware of what analog design is. Such a very incomplete curriculum is a direct path to circuits that don't work.

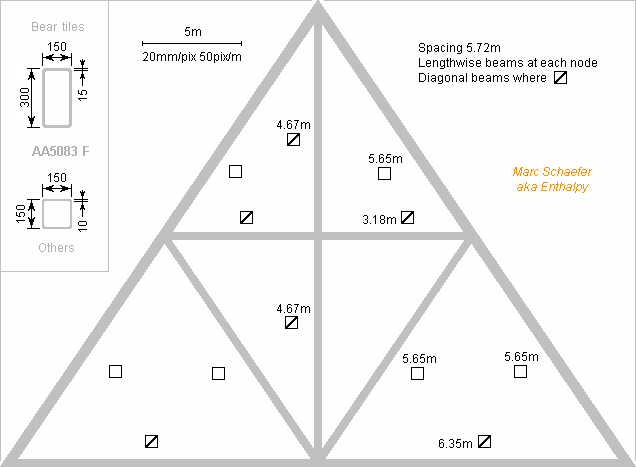
Here's an example of a roof frame made of aluminium beams. Sections and lone beams shall be welded, cleaned and anodized at the workshop, transported by boat, lorry or other (even helicopter), assembled at the cathedral, on top of the walls or maybe on the ground. The idealized roof comprises 19 sections as sketched, but no transept nor conical end that need better drafting tools. The sections are 5.72m apart, with lengthwise beams at each node, plus diagonal beams where signalled. Assembly could be done with: Titanium bolts. Taylor making is cheap. No strong alloy is needed, so favour the corrosion resistance. A believe the bolts need no pre-stress here, which eases galling. AA5754 or AA5083 aluminium rivets maybe (not AlCu4Mg!); anodizing is lost at the holes, but rivets use to be watertight, and the created heads can be anodized at the site. Or break the anodizing where needed, weld at the site, anodize the seams at the site: good with AA5083. For assembly by wedges, ask a woodworker. If oxide densification isn't yet done in the wild, invent the machine. I still apply 100% of 2.2kPa = rho*V2/2 for 60m/s gusts on the whole surfaces. The 5.65m beams under the tiles experience then 50kN*m bending, which loads the 300*150*15 section of AA5083 to 110MPa/2. All tensile and compressive loads, under 100kN, are much smaller than the beams' yield and buckling limits. I take a 150*150*10 section for the other beams to ease their assembly with the flexural ones, no excellent reason. The structure weighs then some 40t, with the tiles 80t for the idealized roof. The design is quite suboptimum, with loads so small. A frame with shorter and more abundant beams would be even lighter. But why? The longest lone beam, 8.5m, fits in a lorry. Taylor extrusion isn't limited to 6m. 300*150 is already big for an extrusion. The profile can be bent and welded from sheet, but long seams have a cost. Possible argument. A 120t roof including the transept costs less than 1M€ aluminium. Assembly must cost more, and more elements worsen it. Thicker aluminium resists corrosion longer if the anodizing is lost. Failures happen at the ends. I ignore what load directions the stone walls accept. If pulling upwards is impossible, the roof needs a minimum weight: 220t estimated with huge margins, and then dry sand would compensate any saved aluminium: I prefer thicker metal then. The roof could be much stronger than this already excessive design, more so with titanium. It could then hold only between the towers and at the transept, to inject no wind load at the walls. It could even hold the walls laterally if desired. Marc Schaefer, aka Enthalpy Bowed instruments design minimizes the stress at the seams, and failure isn't deadly. I've already seen and heard how easily the fragile hide glue breaks under the luthier's tools, and I wouldn't put unknown people under a roof glued like that. You may also notice that instruments are kept in a protective micro-climate. By the way, nearly no old bowed instrument has still its original glue seams. Most instruments were modified during the romantic period, which implied to open the soundbox. More reasons let open the soundbox several times in a century, a routine operation - including when the glue seam breaks, which can happen over time.

This is only a speculation. While other cathedrals did break as spires were built, Notre-Dame looks sound. No visible deformation. The towers are built sturdy up to their top, obviously to support more weight. There can be completely different reasons. Maybe a king was eager to inaugurate and use the cathedral, rather than continue the work and wait 30 years more for his successor to do it. Or some crusade had exhausted the economic and human potential of the country - this is more than a hypothesis: the towers' construction was stopped just before the 7th crusade https://en.wikipedia.org/wiki/Crusades Anyway, we can build the spires now at a fraction of the weight then. That's clear to me too. That way of working is lost and won't come back. Just like many construction techniques are lost: archaeologists observe old buildings and try to deduce what the techniques were, but this suffices to publish a research paper, not to build now with the techniques of then. So I don't consider a second asking present architects to design a building without modern tools. They shall exploit what's available. Think at the analysis of soils for instance, it gives a huge advantage. Or the understanding of lightning impact. And, why not, CAD and finite elements. So I do claim that present architects can plan the (re-) construction of a cathedral better than people in the middle-age - not because they would be more clever now, but just because Mankind has accumulated better techniques. For Notre-Dame's roof, we are lucky enough that we still build roof structures out of wood beams, so it remains an option. And my next sentence began with "More importantly". But, yes, tourism matters a lot to France: it's one of its biggest income sources, together with agriculture, like for other under-developing countries. This fire is a blow to the French economy easily as big as the 737 Max problems is to the US economy. I like this option. But I have interrogations. How long do laminates last? I understand they rely on glue, which I mistrust on the long time. I wouldn't even use a synthetic polymer if it's for a millennium. That won't be the same construction as the original. The roof structure isn't visible neither. So why not go directly to reliable materials, that is, metal? Metals creep very little and are very little subject to fatigue. These behaviours are even predictable. They expand zero with humidity and little with heat, in a predictable manner. To add a roof over high thin walls of undocumented and old stone construction, I prefer to fully trust at least the roof materials.

With metal beams, there would have been even less fire damage. I ignore why the spires were not built. The towers are obviously meant to carry much more weight - just observe the sections up to the present top. The spires were in the plans in 1160 but abandoned in 1240, I haven't read a reason. With present materials, they would weigh a fraction of what was possible then. The very Notre-Dame shows that builders do how they are used to within their time. The construction spanned two centuries (if you allege it's finished without the missing spires) and the style is hybrid, the techniques too. Most other constructions had their plans heavily modified over time, before or after "completion". Check for instance the Stephansdom in Vienna, St Vitus in Prague... about every cathedral Construction of Notre-Dame (English) Construction of Notre-Dame (French, other details) Stephansdom Saint Vitus in Prague In Notre-Dame, the transept was added later and their front increased even later, and so on and so forth. Don't overestimate neither the knowledge of middle-age architects. Many of their buildings collapsed, others (cathedral in Strasbourg and more) could not be finished because their design was flawed. That some buildings still stand is an achievement, but don't presume present architects would do it worse. Many Parisian buildings date back to 1850-1870 Haussmann and are on the best way to last centuries more. If willing some sort of "original state", then I would like colours to be restored. Cathedrals were brightly painted, the inner walls, the statues... Colours fainted over time or were destroyed, for Notre-Dame when a bishop or canon let cover all walls in white in 1756 and replace stained glass by transparent one. What we see now is an ugly and badly degraded remnant of the early state. Keeping naked stone walls as is, or restoring them to their degraded state, is not a goal for me.

I agree. Apparently there would be enough oak in 2019 to rebuild the roof, but the parts would be smaller, which imposes to adapt the design, and the wood is still trunks in the forest. Such sections take a decade to dry, and if one tries to accelerate, the wood splits, and if the wood is used wet, the roof deforms. I doubt the French want to wait a decade to start rebuilding. The president told "rebuilt in 5 years". With metal, it can be finished in less than 2 years. It does make an economic difference whether visitors can come in 2 years or in 15 years. More importantly, "already healed" rather than "still wounded" makes a difference for the Parisians and French. This is decoupled from the colour. Having lived just in front of the South side of the cathedral, I find it ugly, both in shape and colour. Rebuilding is the opportunity to improve that - obviously a matter of taste, and not a need. Both aluminium and titanium (niobium too) could be given the colour of old lead. After receiving the blow, "rebuilt nicer than it was" is for me a better answer than "repaired as we could". The picture shows the smoke flying into the towers where the firefighters were, then horizontally. Many Parisian buildings are taller than that. Smoke later falls down, that's why you smell wood fires in chimneys in towns. Due to density, lead smoke falls faster. The Church seems richer in Britain. In France it isn't, nor is it perceived so. The buildings were confiscated by the Republic and often in need of repair, priests are not paid by the State except in Alsace and Moselle. If one explains "gold colour" the French grasp the difference. If aluminium is cheaper than oak, even better.

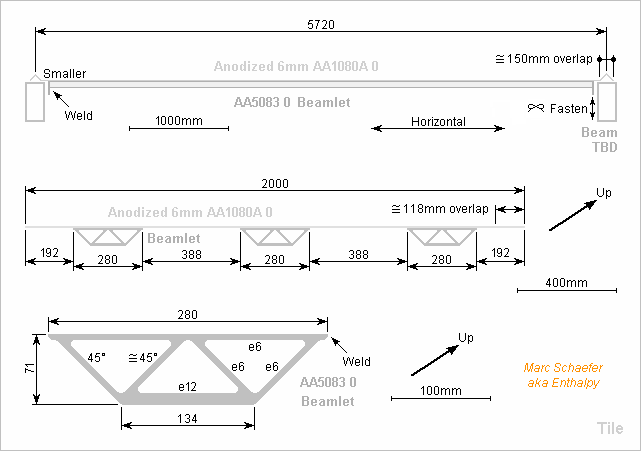
My proposal for a new roof: aluminium tiles. 6m*2m sheets are common, and the well-proven anchors in the walls shall serve further, so the main beams are 5.72m apart as were the burnt ones, and the sheet and tile length is horizontal. A higher tile overlaps a lower one, and the short sides are folded in lambda shape to repel water. The overlapping lambda is bigger to allow for thermal expansion. 60m/s gusts shall load the parts to half the yield stress. I apply 100% of 2.2kPa = rho*V2/2 on the whole surfaces. Eurocode 1991 would do that better. The outer surfaces are of AA1080A with thick anodization for corrosion resistance and aspect. 6mm thickness and 388mm between the beamlets load the sheet to 15MPa/2. Purer alloys are badly standardized but can be tailored for that amount, in thicker sheets to keep the strength. Or use titanium, with less colour choice. Without the transept, the 102m long roof needs 216 tiles, and the sheets weigh 42t. Humidity condenses occasionally under the roofing, so the beamlets are of AA5083. Tailor-made extrusion and some 5.4m length load the alloy to 110MPa/2. The chosen angles shall let humidity flow along the surface, not drip down. Three beamlets per tile contribute 49t to the idealized 102m roof. The tiles hold at the beams by AA5083 end plates welded at the beamlets. Cold-drawn AA1080A wire can make corrosion-safe fastenings. I want all weld seams airtight, between the sheets and the beamlets, and between the beamlets and the end plates. The beamlet-to-sheet seams must be much thinner than 6mm to preserve the exposed face's composition. TIG, MIG... or even FSW are possible. These alloys make seams with full strength and corrosion resistance. A tile is fully made at the workshop: fold the sheet, weld the beamlet ends, file and clean, weld the beamlets on the sheets, clean, anneal the whole tile. Anodize at least the exposed face, but the inner face including the beamlets wouldn't hurt: grow thick oxide, soak with pigment, densify the oxide. Main beams later and maybe. Good night! Marc Schaefer, aka Enthalpy

Here I've added the missing elements, hoping to inspire an architect. The roof has also a stable colour possible with anodized metal. That is a cathedral rather than a clumsy building. The roof colour can be finely tuned, with titanium or more freely with aluminium. It could match clean brass, as were the roofs of Paris' monuments few years ago, or as was Lübeck's cathedral before getting the green patina. I feel it incomparably nicer than grey lead, whose only advantage is to match pigeon droppings. Vast openings reduce the wind load if useful and give room for the bells that were so badly located under the lead roof. I get accustomed to the view faster than expected. Marc Schaefer, aka Enthalpy Hey JC, you will fool about nobody with that attempt on a forum for science. And I know with full certainty that you don't believe a second what you write. Anyway, here's again one picture showing that pollution doesn't dilute instantly over the whole Parisian atmosphere: Fumes flying right into the towers with the firefighters. I hope they will decontaminate all clothes and tools. The fumes fly then horizontally, and many Parisian buildings are higher than that. Not to forget that the fumes fall down as they cool. Lead vapours oxidize to make fume, or less probably condense into an aerosol. Then they fly away as ash, cool down, and are inhaled by people downwind. Vapour pressure matters to tell that lead first gets in the air. ========== Bizarre. A French NGO that told more or less the same was threatened with cutting their subsidies. On an other forum, my similar contribution was obviously not appreciated at all. But this was all on French websites, where this is expected.

No understanding needed. See the pictures.

Here are pictures of some gothic and neo-gothic cathedrals: Do you guess what is missing at Notre-Dame de Paris? Besides the roof, I mean. It makes it so clumsy. They were foreseen initially but quickly abandoned. Viollet-le-Duc planned them when restoring the cathedral in the 19th century but he didn't have the moneys. My opinion is that they could be built now, especially since oak would take years to dry and modern construction techniques make a cheaper roof. And what air amount at 50m distance, where the firefighters were? At 150m, where the first buildings are? The plume had around 50m*50m section. Put the figures together: that's an extreme concentration.

Thinking more at the yellow smoke: On pictures of the attic, I saw only the lead roofing, the oak structure and wooden floor, plus dust that may explain how fire started, as lighting oak in a chimney is badly difficult. I did see thick smoke when lighting wood, but this one was stone-dry. Half 1.5 century old, half 8 centuries, under a roof. The rest, lead, has a known yellow oxide. Much of the lead escaped the flames when melting, but a part felt on burning wood. Some beams were horizontal, and from the pictures the wooden floor was everywhere. If only 1% of the lead ended on burning wood, it made already tons, up to 100% or hundreds of tons. In the big fire, lead evaporated and oxidized. With 0.01atm vapour pressure at 1400K, evaporation goes quickly. I had considered lead oxide as a possible explanation. Presently, tons of lead fumes seem unavoidable to me. And my comparison with a known situation was already an attempt to reduce the uncertainty! I definitely agree that assessment is badly difficult from my armchair. But I have zero dot nothing confidence in what the French government may tell on this topic, as history already showed. Beyond the duration, the amounts shouldn't be forgotten. As lead exits the organism very slowly, it's more or less their product that counts. Here there were hundreds of tons (or tons if most lead flew away) at flame temperature rather than many kilograms at 1210K. Or just compare the volume of yellow fume, clearly worse than at a smelter. Between the amount of lead fumes, say tons, to the amount noxious in a human body, a milligram, the ratio is one billion. This ratio suggests the noxious amount will be exceeded at many people. A noxious amount of lead in a human body is only 1x to 10x the amount for cyanide. If 100kg of cyanide were released in the atmosphere in the middle of Paris, more people would wonder how dangerous it was. Or rather, we would already know, as cyanide acts faster than lead. For the firefighters in the towers, the fume dilution was minimal, see the pictures. I dearly hope they used respirators and decontaminated their clothes and equipment afterwards. People on the ground nearby seem less exposed as the fumes escaped horizontally on the pictures, but inhabitants downwind received copious amounts.