Enthalpy

You can hear the existing Glockenklavier, Wagner's attempt to implement the Gralsglocken, at br-klassik.de qUfo1szjPIc pcpkp13juVA at 0:30 to 1:24, younger version with mallets 3mNMUNJIS3Q at 0:30, 1:00, 1:31 and 1:48 older version with keyboard

One more example of nice sound on a soprano tárogató by Attilio Berni v0tFp2_H3R8 at 8:50 many more saxophones and similar instruments on this fascinating record.

I breadboarded all the circuits. I don't quite remember where I saw the claim of a voltage gain, maybe National Semiconductor's Linear Applications, or some source that is rarely wrong, unless I wouldn't have believed it. So I just built the RC circuit and measured. Once I had seen a voltage gain with a generator and oscilloscope, I built the two oscillators, and both ran smoothly. I've made no use of this up to now, but it debugged a misconception ("RC circuit has no gain") of which I was quite sure. ========== And just for fun... As I worked on active filters in the worldwide electronics research lab of a multinational company, I tried a state variable biquad cell where one op amp in a feedback loop was to provide a phase lag, so if all op amps in a package had the same Gain-Bandwidth Product, the phase lags would compensate, and this cell would be insensitive to the op amps' limited bandwidth. Nice idea. Found in a very reputable book about active filters, written by my professor, a known guy for filters. Unfortunately, that magic biquad cell oscillated. I tried two more biquad circuits from that same book, and all oscillated. Putting some thoughts and equations on it, I found they had to be unstable. So the well-known professor had put b*llocks in his reputable book, having computed a transfer function but not checked the stability, and without having breadboarded anything. I already knew such things happen. Then came my bosses of the research lab, who were all unable to use a soldering iron nor an oscilloscope, and asked me to demonstrate that a Sallen-Key doesn't oscillate. Man, I tried to explain that it would have been known for long, but they insisted. Then - and I had already tested the oscillators of the first message here - I answered "the Sallen-Key is stable because the buffer op amp has a gain <1 and the RC network too, so nothing can oscillate" and that way I got of their stupid query.

The luthéal is a less common instrument... A historical one is in Brussel's Musée des Instruments de Musique, one built more recently is in Paris' Musée Instrumental, one was built for Daniel Hope, and apparently that's all. George Cloeten patented it in 1919 as extra hardware on a piano to change the timbre at will, plus controls available to te pianist. wikipedia And there are records of this instrument, even recently : mim.be GuiPX6BVSkg on Youtube at 9:39 (the piece starts at 05:33) Two (2) known pieces were written for the luthéal, both by Maurice Ravel, but are commonly played on a normal piano: L'enfant et les sortilèges, and Tzigane. I had always felt that the piano's entrance at the fourth minute of Tzigane was to imitate a cymbalum and, in a symphonic orchestra, would better be played on a cymbalum. It's clear now that Ravel wanted a luthéal to imitate a cymbalum. In my opinion, where no cymbalum is available, or isn't loud enough, one or two percussionists would better play the score on the strings of a grand piano using wooden mallets. The mallet heads must be tall enough to reach the strings below the frame, and some visual marks would help. Marc Schaefer, aka Enthalpy

The Japanese koto and other string instruments have their soundboard made of Paulownia tomentosa (kiri) instead of spruce Koto at Wiki - wood-database.com - Paulownia at Wiki This broad-leaved tree provides lighter wood than conifers, even spruce: 280kg/m3 against 400kg/m3. Its lengthwise E-modulus is 4.4GPa against 10GPa, so the figure-of-merit E/rho3 is 200 against 156 for flexural wave speed at identical mass. Its fracture stress is 38MPa against 70MPa, so the figure-of-merit sigma/rho2 is 485 against 438 for bending resistance at identical mass. I have no other data: ER, ET, acoustic losses, ease of working... It grows very quickly, at Australian producers too, but the tree is undesired in the US hence its wood rare and expensive there. Japanese luthiers use it traditionally, so its other properties are known. At the linked wood-database.com, one luthier tells she prefers it over spruce for guitars. Worth a try at pianos? Bowed instruments? Others? At identical resonant frequencies, it would make soundboards lighter, hence louder and more responsive hopefully. Marc Schaefer, aka Enthalpy

For the evolved Glockenklavier, tensile soundboards promise efficiency: they store hence dissipate little vibration energy, and their minimal mass couples well with the strings and the air. ========== Materials Somehow I don't trust wood under permanent extreme tension. It's also too fragile and, under achievable thinness, too stiff to my taste: any residual bending at a bridge would break it under tension. Maybe I'm unfair. Plain polymer films aren't strong enough. PEN (polyethylene naphthalate) outperforms now PETP de.wiki - en.wiki 1360kg/m3 and 380m/s sound speed would need 196MPa tension, but PEN films break at 200MPa and creep well before. The films still elongate by 60% at break, and I suspect much stronger deformation at production would make them stronger. Graphite or polymer fibers are by far strong enough. Unidirectional graphite composite weighing 1550kg/m3 needs only 273MPa for 420m/s and guarantees often >1200MPa. At least in ropes, some polymer fibres offer similar strength-to-mass with better flexibility and good (sufficient?) creep resistance. Rather than using some epoxy matrix, one could ask a sails maker to embed the fibres between two polymer films: the usual thickness fits the soundboard better, and sail makers design with stress in mind. My clear choice is cold-laminated stainless steel. 7900kg/m3 and 380m/s need only 1141MPa while austenitic steel band can guarantee >2000MPa and more, with negligible creep. Carbon steel showed a frightening notch sensitivity in my trials, but AISI301 was very tolerant even at >2000MPa strength, and gained further resilience and strength after a short 180°C bake. I stressed such bands at 1000MPa for months and they performed perfectly. Such a band resists corrosion, is easy to process at 50µm and 100µm thickness and is available from industry suppliers. Other alloys, like duplex stainless steel, PH 15-7 Mo, Maraging or CoCr20Ni16Mo7 can be strong enough but I discern no advantage to them. ========== Sound radiation Individual mills limit the width of ultra-strong bands; I take a soundboard 1m high, to be checked. Width is for instance 5m and the deformation taken as a sine. At the E=41.4Hz fundamental, the soundboard is not so big, so I take 5.6mohm*F2=10ohm radiation resistance. 1m/srms at the centre moves 3.2m3/srms air, so with a closed soundbox, the radiated power is 100Wrms. 100µm steel is sturdy and easy to process. The 1m*5m soundboard weighs then 4kg, so the same vibration stores 2J. A free vibration decays in 20ms or one cycle of E=41.4Hz. Higher frequencies radiate even better as they propagate faster in the band than in air, and will decay in fewer cycles, that is, before reaching the end of the band. The slow membrane of a banjo radiates slowly and its densely packed resonances create a completely different sound. Since usual metals Q-factors are in the thousands, if the rest is properly built, this soundboard is nearly 100% efficient, while flexural wood achieves 10% or less. Loud instrument. This soundboard is essentially aperiodic. I expect it to add no colour to the sound of a bare steel string heard by skull contact. Nice sound, resembling more a bell than a piano does. ========== String coupling Usual soundboards of flexural wood are heavy and stiff, so a very light bridge transfers little string power to them. Here the soundboard is but heavier than one string and radiates immediately any received energy, so something like the bridge must limit the power transfer for good power and duration. A stiff bridge looks better than a heavy one for that, as it transfers better the higher frequencies, so the high partials will be stronger at the beginning of a sound and vanish more quickly, as from a bell and most instruments. The bridge's resonances should be damped. The non-speaking string length contributes stiffness too. Such a soundboard seems useful to more instruments. Marc Schaefer, aka Enthalpy

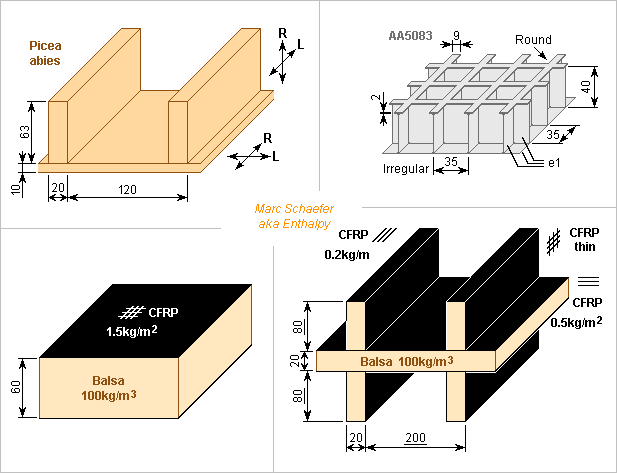
Here are attempted flexural soundboards for the Glockenklavier evolution. To radiate low frequencies well, a soundboard must spread the vibration wave over much area, and if several locations have opposite phase, they should be far apart with different areas or amplitudes. This favours a big flexural propagation speed. At high frequencies, the many locations with opposite phase can still reinforce an other in directions where their path difference is a half-wave, which needs a flexural propagation faster than the sound in air. This justifies Picea abies (spuce) among usual materials and shapes, with ribs and domes. The E=41.4Hz Glockenspiel, with a 5m string, woud have a soundboard about as long. ========== Wood Picea abies could have transverse fibres in a 10mm plate and tall lengthwise ribs. The bridge shall spread the vibrations sidewise, big assumption. With rho=360kg/m3 and E=11GPa, I find flexural 342m/s in the plate at 1.2kHz and lambda/2=0.14m, and take ribs spaced by 0.12m. Ribs 20mm wide and 63mm tall give EI=3.8*104 and µ=8kg/m2 for the complete soundboard, so EI/µ=4.8*103 m4s-2. At 52.1Hz, the mean of E=41.4Hz to C=65.7Hz, lambda/2=1.4m, wasting a longer soundboard, and the cutoff frequency is 269Hz, not exceeded until the 7th harmonic of 41.4Hz. This reveals an inefficient soundboard, and it's heavy too. Even grand pianos have a stiffening bulge in the soundboard despite the many strings in a plane, so the above attempt isn't optimum. Strong camber gives its plate much stiffness, so the koto instead should inspire the Glockenklavier wikipedia make the hull a good portion of a cylinder but flexible at the sides, put transverse ribs from place to place, tall at the middle, and fasten a tall keel under the top's centre. The keel must reach the hull, it can have apertures and be thicker at the bottom. Roughly, if this design puts wood 4* farther apart and better spread, it's 100* stiffer, so waves are 3* longer. Hugely better, but I won't detail it. I suppose a wooden soundboard wastes in internal losses >90% of the input vibration and radiates the tiny rest, worse at low frequencies even with a better design. Neither do I want the piano's wooden sound for the Glockenklavier. ========== Milled aluminium I limited to 40mm the dimensions of 1mm milled walls, and then aluminium brings only EI/µ=2.7*103 m4s-2, worse than Picea abies. Though, a refined design with a few taller parts would improve, and AA5083 or AA6082 are easily welded. At least, aluminium loses less power than wood and should sound metallic. Irregular cell size shall limit the resonances. ========== Graphite fibres sandwich Flexural waves run slower in graphite composite (CFRP) alone than in wood, so here's a sandwich with 60mm balsa core of 100kg/m3 and 2*1.5kg/m2 skins of 1550kg/m3 and isotropic E=90GPa for total µ=9kg/m2. I doubt balsa transmits shear stiffly enough, especially for shorter waves, so it's probably interrupted by tilted fibres resembling corrugated cardboard. EI/µ=18*103 m4s-2 improves over wood. At mean 52.1Hz, lambda/2=2.0m, nothing magic, and heavy too. At violins, cellos and pianos, present CFRP soundboards sound horribly because they resonate too low, which the core improves. Balsa should also limit the wild resonances. Or it's wishful thinking. ========== Graphite fibres with ribs Between lengthwise ribs, transverse fibres and 20mm balsa shall transmit the vibrations over 2*0.1m. 80mm*20mm balsa ribs spaced 0.2m hold lengthwise (190GPa) 0.2kg/m CFRP at the outmost faces, and thin isotropic CFRP covers everything, for total µ=6.6kg/m2 and EI/µ=300*103 m4s-2. At mean 52.1Hz, lambda/2=4m gets usable, and the soundboard is lighter. The cutoff frequency is below 41.4Hz, perfect. 40kg are still a bit much for 1kg contrabass strings. PU foam is lighter than balsa, but is it stiff enough? This plate too can adopt the koto shape with ribs and keel. Or a bridge, for instance cable-stayed, can inspire its shape. wikipedia Marc Schaefer, aka Enthalpy

The horizontal harp proposed here on February 24, 2019 could get a frame of cast magnesium alloy. Passing in the soundbox, it looks easy, lightweight and cheap. Magnesium, optionally the same part, perhaps with integral ribs, might compose the bottom and sides of the soundbox too. Fibre composites too might make the frame and optionally the faces of the soundbox not meant to vibrate. Of course, I have nothing against other alloys like aluminium or zinc, nor against assembling parts. And absolutely nothing against wood. Marc Schaefer, aka Enthalpy

Rods would be made by extrusion, not injection, so the unusual resin costs no new tool.

Rods would be made by extrusion, not injection, so the unusual resin costs no new tool.

In this discussion on December 16, 2018, I suggested graphite-loaded polymers to replace ebony at fingerboards and other parts. Besides better known POM and PEEK, liquid crystal polymers are available as pellets too, and their properties seem excellent for parts of string instruments. A decently documented LCP is Vectra, from Ticona=Celanese: hipolymers.com.ar Compositions page 11: A is the most common base resin, E would have had higher losses. 9nn is pure, 2nn contains graphite choppers. Vibration damping page 22. Pure Vectra A950 has losses ~6% and E~10GPa while Dalbergia melanoxylon has losses ~0.6% and E~20GPa lengthwise, but E drops a lot in the R and T directions. With 30% graphite choppers, A230 offers ~3% losses and E~30GPa, stiffer than ebony. Lossy materials may improve the parts of string instruments that shall not vibrate - maybe, as theere is some debate about the violin's fingerboard. Can a musician safely hold this material in his hands many hours a day for 50 years? I'm no expert, but at least the unloaded resins A950, B950 and C950 are compliant with FDA regulations for food contact, page 33. I suppose Graphite choppers don't harm. Far less nice, the price page 11 is somewhere between PEI and PEEK, ouch. Neither did I see rods for sale, only pellets meant for injection, but Hoechst-Celanese did provide rods of A950 to a research team. Shall the luthiers contract a plastic injection company to make rods for subsequent machining, or rather to inject the net instrument shape? Good to know: Vectra gets anisotropic upon injection. Datasheets of A950 and A230: Selection - A950 - A230 at tools.celanese.com The A950 composition shows better Charpy (break by shock) figures than POM. Resilience drops with graphite choppers. Both compositions absorb very little moisture. Marc Schaefer, aka Enthalpy

They are well known as top-performance fibres, but liquid crystal polymers are available as pellets too, and their properties seem excellent for music instruments. A decently documented one is Vectra, from Ticona=Celanese: hipolymers.com.ar Compositions page 11: A is the most common base resin, E would have had higher losses. 9nn is pure, 2nn contains graphite choppers. Vibration damping page 22. Pure Vectra A950 has losses ~6% and E~10GPa while Dalbergia melanoxylon has losses ~0.6% and E~20GPa lengthwise, but E drops a lot in the R and T directions. With 30% graphite choppers, A230 offers ~3% losses and E~30GPa. Stiff and lossy materials are rare and supposedly make better woodwinds. Can a musician safely hold this material in his hand and blow in it many hours a day for 50 years? I'm no expert, but at least the unloaded resins A950, B950 and C950 are compliant with FDA regulations for food contact, page 33. I suppose graphite choppers don't harm. Far less nice, the price page 11 is somewhere between PEI and PEEK, ouch. Neither did I see rods for sale, only pellets meant for injection, but Hoechst-Celanese did provide rods of A950 to a research team. Shall the luthiers contract a plastic injection company to make rods for subsequent machining, or rather to inject the net instrument shape? Good to know: Vectra gets anisotropic upon injection. Datasheets of A950 and A230: Selection - A950 - A230 at tools.celanese.com The A950 composition shows better Charpy (break by shock) figures than POM. Resilience drops with graphite choppers. Both compositions absorb very little moisture, excellent. What shall be the first trial: a piccolo or an oboe upper joint? And I want a bassoon of it! Marc Schaefer, aka Enthalpy

Hi DrP and all, While the Glockenklavier was designed (and failed) to replace church bells, it is a string instrument adapted from a grand piano, and it does sound like a grand piano. Here it there: 3mNMUNJIS3Q at 0:30 with keyboard pcpkp13juVA at 0:36 with hand hammers The vibraphone has metal resonating bars, much like the glockenspiel, but it's lower and it adds tubes to amplify the sound. You can view it as a marimba or xylophone where metal replaces the wooden bars. And because Sapiens sapiens have imagination, here's an attempt to replace low bells with metal plaques and a vibraphone on steroids: 5SvuGtaU3Co at 0:42, 0:55 and 1:09 the sound is less clean than from a bell, but it definitely resembles, far more than the Glockenklavier does. Passing over a symphonic orchestra's fortissimo is quite doubtful, what the Glockenklavier can't neither.

Yes, most of you have already heard one, and even many... But most often, both the musicians and the composers make it a lumbering instrument, which it is not. So here are examples, all on Youtube. zPQdXN7wZcM les Tubadours fYOsNp4O7AU Øystein Baadsvik GNjsxLdSwHI Andreas Martin Hofmeir Far more agile than most listeners and musicians imagine.

Can the Glockenklavier improve? It will never sound like a church bell, but it's half manageable and affordable, and Wagner wanted it for Parsifal de.wikipedia - wiener-staatsoper.at - br-klassik.de Steingraber made the 1882 instrument with bits of his grand pianos, and the loudness and sound resemble more a piano than a bell, so here a a few proposals. Felted wood hammers can't imitate an iron clapper against a bronze bell. Better bare plastic, beechwood or bronze. 8 piano strings per note make the sustain fainter and even longer, wrong choice for low notes. 1 string per note. The 1914 instrument had no keyboard but hand hammers, enough to play single notes in Parsifal. The 8 strings still needed hand hammers of ridiculous piano style. Have good heavy rods instead. Or move the hard and heavy hammers with foot pedals, sturdy as for a bass drum. Hydraulic transmission is an option. Strings make a brighter sound if they propagate the wave faster than air does. At D=5mm, Röslau delivers 1720MPa steel. 18-12-5 maraging steel gives 2400MPa at any diameter. No copper overspinning. I don't care about harmonicity. At 380m/s, strings are 4.5m long for E=42Hz but cold-drawn steel has only 1.5* strength margin. Maraging achieves 420m/s for 5m strings with 1.7* margin. 6m bars are standard and the instrument fits in a lorry. The soundboard can be vertical. If the sound is more brilliant sideway, consider reflectors. The strings should face the public. The musician can have a mirror. End fasteners can be welded on maraging strings. Friction can hold cold-drawn carbon steel, but with self-blocking shapes like pairs of cones, as the string thins under tension. At the two bridges, maybe slit or split cylinders can be screwed tight on the already stretched strings. A single instrument can have its frame similar to a grand piano but of welded steel tube. The soundboard is wider than the 5m string speaking length and tall. I'd have a closed soundbox to radiate the 42Hz. It could consist of spruce planks and ribs like at a piano, or maybe of aluminium as we want a metallic sound anyway. For flexural propagation speed similar to spruce, aluminium sheets must be milled thin with tall integral ribs, and can be welded butt. Can instead a thin soundboard get its sound speed from tension? The strings move more easily a very light soundboard, and propagation faster than in air radiates all frequencies well. Cold-rolled steel achieves is easily (>920MPa tension), composites even more (>200MPa for 1700kg/m3), aluminium with little margin (>330MPa), some plastic films (>150MPa for 1300kg/m3) and even luthier-quality Picea abies (>42MPa for 360kg/m3). I suppose the board must be thin enough so radiation dampens the resonances, and its resonances tuned outside the spectrum of the four notes. Side reflectors seem necessary. The bridge and frame may have to slow down the energy transfer from the strings to the soundboard. Tensile soundboards exist already at banjos, qanuns and many more, but with a slow propagation. Fast tensile soundboards would apply to more instruments if they sound well. As a hypothetic killer option, extra items could be made to knock at the note's frequency against the strings or other vibrating parts. At the snare drum, the banjo, the tromba marina and others, it takes power from the fundamental to replenish the high harmonics that make the sound much more powerful and brilliant. The knocker needs an extremely accurate adjusted position (the tromba marina lifts one foot of its bridge), or it may have a spring and rely on its inertia, or few knockers among many can have by chance the proper position. Would the usually strident effect fit a Glockenklavier? Less hard materials nearer to vibration nodes have a less extreme effect. The development of this instrument requires luthier skills only if the soundboard is of wood. It's more acoustics and mechanical engineering, not very costly. Delicately megalomaniac thesis topic for instance. Marc Schaefer, aka Enthalpy

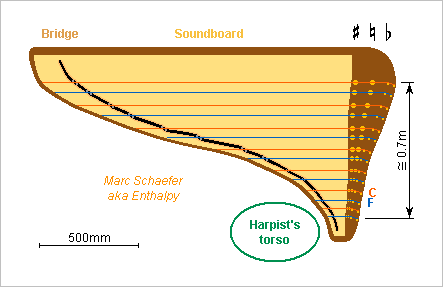
If a harp's string plane is horizontal and the musician plays from the top, the lower side is available for a big, unstressed, lound soundboard. A double-action diatonic concert harp could resemble a qanun and other zithers: 14 to 16mm spacing spread the 47 strings over 0.7m, letting small harpists lean forward or backward a bit. Both hands access the full range if needed but risk to collide at high notes. The playing technique is the same as on a vertical harp, excepted the less comfortable hands position, and I expect harpist to adapt swiftly. The equivalents of près de la table, sons xylo, harmonics and others look possible. The space between the natural and sharp disks can be straight, as on the sketch, for better action designs. Or the sharp disks could be aligned, or the soundboard's edge straight, and more - the strings middle line seems decent on the sketch, but the hands could look more to the right at high strings. Alternately, the action parts could reside below the soundboard, with plenty of room for a better design. A post for the pedals would usefully be removable or foldable, making the thinner instrument easier to transport than the vertical harp. The construction resembles a grand piano, notably the bridge where the strings can zigzag at two pins to inject no force in the soundboard, though a single downward bend might be good too. Stiff bracings and a closed box would give a deep sound; this can be adjusted to differ less from the vertical harp. An optional sound hole would reinforce low notes down to a cutoff; I'd put it at a side, not at the soundboard, and a rosace or many small holes would tame the resonance. Resonating doors, as described in this discussion on 03, 05, 07, 09 February 2019, apply here too. To be easily strong and stiff as on a piano, the frame can run under the soundboard rather than around it, best through the soundbox, and be of metal, wood, fibres... A removable hard cover, or a complete box, must protect the soundboard and strings. ========== A chromatic version would be simpler and could have two bridges, but as usual, it can't play the existing harp scores, and low strings must keep the 16mm spacing to avoid collisions, so the range takes an impractical span. The soundboard could carry several string groups side by side as on the cimbalom. This limits the playing technique. Or the individual range must be reduced and spread over two instruments. Good opportunity to start the low harp at the piano's A. 49 strings would then cover 4 octaves, and the high and low chromatic harps overlap by 1.5 octave. Marc Schaefer, aka Enthalpy

The best musical strings are still made from gut, possibly spun with metal wire. Gut is often replaced with PA11 polyamide or with metal, but nothing provides the crispy, profound and long sound of gut, for reasons not fully understood. Strength per mass unit is mandatory, very low mechanical losses too, density and bendability are useful, and I believe elastic strain matters. "Catgut" is one sheath of the lower part of the intestine of sheep, sometimes goats or cows, after mechanical and chemical processing which I understand leave only the collagen, in fibres oriented essentially lengthwise gamutmusic.com and web.mit.edu The upper part of the intestine made sausage casings, but for decades collagen widely replaces it because the process is simpler wikipedia Similarly, it would be nice to make musical strings of collagen, where at some process step collagen would be a homogeneous melt or solution, to obtain more easily strings of repeatable properties. The cited Wiki paragraph, brief and not quite clear about it, mentions: "It is widely used in the form of collagen casings for sausages, which are also used in the manufacture of musical strings." but I've never heard about a musical string made of collagen, far less a good string, so there must be hurdles. Yarn from collagen exists already and serves for medicine. Citing subchap 2.4 of: Biomaterials Science: An Introduction to Materials in Medicine By Allan S. Hoffman, Frederick J. Schoen, Jack E. Lemons "Reconstituted collagen is obtained by enzymatic chemical treatment of skin or tendon followed by reconstitution into fibrils. These fibrils can then be spun into fibres..." Gut is a raw material long enough for strings, but to spin fibres, tendon seems an interesting alternative. Or continue with gut if the strings are better. Wiki suggests that the exact spinning method is paramount to stretch and orient the macromolecules and transform weak polyethylene into ultra-strong Dyneema and Spectra Polyethylene fibre and Gel spinning at Wiki it seems logical: the lower exit temperature in gel spinning keeps the order acquired by the macromolecules in the spinneret. Whether this achieves strings as good as gut? Marc Schaefer, aka Enthalpy

Musical strings stretch the strongest materials to their limit. The string sound speed sqrt(sigma/rho) is 300 to 500m/s in music instruments, and where a string must be shorter, it is spun with metal wire over a thinner core that is still extremely stressed. Examples: Violin E. 662Hz, 325mm, 430m/s. Plain steel, 7850kg/m3 needs 1455MPa tension, and many E strings are overspun with aluminium wire. Was gut in the past, then estimated 1000kg/m3 needed 185MPa. Harp Eb. 625Hz, 287mm, 359m/s. Plain gut, 1320kg/m3 needs 170MPa. Harp Gb. 2973Hz, 78mm, 463m/s. Plain polyamide, 1040kg/m3 needs 223MPa. Piano C. 4186Hz, 48mm, 402m/s. Plain steel, 7850kg/m3 needs 1268MPa. Plucking or striking the string increases the stress further, in addition to bends at a knot, bridge or nut. For strength, polymers are drawn to wires, which stretches the macromolecules. Hardened high-carbon steel is cold-drawn to harden further. roeslau-draht.de >1720MPa for D=5mm to >2790MPa for D=0.28mm. I mean, wow. ========== Is different steel possible? Austenitic stainless steel exceeds 2000MPa by cold-working. Quality Strings alleges it's abandoned because it cracked more easily when flattened qualitystrings.com but I experienced the opposite with 2000MPa cold-laminated band: notches kill carbon steel band while the 17-7 alloy can be bent flat with a hammer after short tempering around 180°C which improves both the resilience and the proof stress. Tempering uses also to reduce the vibration losses, which I suppose were the real disadvantage. I doubt 17-7 attains 2700MPa but it retains more strength at bents and knots than carbon steel does. Duplex stainless steel behaves much like austenitic. Precipitation hardening austenitic stainless steel hardens by aging after cold-working, easing the effort. The PH 15-7 Mo spring alloy is documented to 1800MPa only but mechanical uses probably didn't exaggerate the cold work enough. Martensitic and ledeburitic stainless steel behaves much like carbon steel. PH 13-8 precipitation-hardens to 1400MPa, so prior cold-drawing may give a good hardness. Maraging steel is seducing. 18Ni12Co5Mo1Ti bring 2400MPa by aging, even at big diameters, with much resilience worth more than brittle 2800MPa. 50% reduction hardens the 18Ni9Co5Mo1Ti from 1900MPa to 2400MPa for instance diccism.unipi.it A violin or a piano afford easily the 50€/kg. Maraging would not rust, even at finger contact, but it can trigger allergies if bare. ========== Other alloys? The cobalt alloy CoCr20Ni16Mo7 similar to maraging steel resists corrosion better than needed. It can trigger allergies if bare. Its strengthening by cold work is documented matthey.ch 1920MPa @60% reduction, 2290MPa @90%, can increase further. Thicker strings of lighter metal may sometimes be better. A violin E string thicker than 1/4thmm would be more comfortable, it might be less prone to hiss and stick better to the bow. Thicker piano bass strings would carry the heavy copper wire in a single layer, which some manufacturers prefer pianopricepoint.com Titanium alloys resist corrosion. Ti6Al4V, Ti6Al6V2Sn, Ti10V2Fe3Al attain by ageing 1100MPa, or the same sound speed as 1950MPa steel, and the same elongation as 2050MPa steel. The equivalent of 2600MPa demands 1470MPa from titanium, hopefully obtained by cold-working. A titanium core of identical mass would be 1.7* stiffer than steel against bending, which has no consequence at a piano bass string. Exotic aluminium alloys attain 810MPa, for instance the RSA-707 made by RSP by rapid solidification and sintering. Same sound speed as 2200MPa steel. Maybe this one, or more common ones like AA7075 (480MPa), attain by cold-working 950MPa, the equivalent of 2600MPa steel. Cold-rolling brings the AA5456, which would resist finger corrosion, to 432MPa at 60% reduction and 487MPa at 80%, so more is possible. High-Pressure Torsion brings AA7075 to 1000MPa and the corrosion-resistent AA5083 to 900MPa nature.com while High-Pressure Sliding, better suited to wires, brings AA7075 to 700MPa researchgate.net they apply to titanium alloys too, but I've seen only the superplastic properties. Metal matrix composites improve the strength-to mass ratio of metals, but they tend to increase the E modulus too, and I suppose they dampen more. ========== Polymers? Polymer ropes of aramide, polyester or polyethylene are lighter than steel at identical resistance cousin-trestec.com exceeding 1000 or 1500m/s sound speed, equivalent to 18 000 MPa steel, but they sound "poc" when plucked. I suppose that braiding, impregnation and cover create damping by friction. Just twisting, possibly twice as in a steel rope, must be better. Polyamide musical strings are monofilament (and don't equal gut sound by far). Polyester and polyethylene get strong by fine extrusion, so quite possibly they must stay multi-filament and keep lossy. How would metal-spun Dyneema sound, properly assembled and stretched, no idea. Ropes thrive to minimise the strain, but musical strings need elastic elongation. That's one simple property where gut outperforms polyamide. The stiffer para-aramide uses to make ropes and meta-aramide fluffy heat-insulating material, but yarn exists too teijinaramid.com Meta-aramide has 1/4th the strength of para-aramide as a fibre. If it retains that factor as a string, it attains 500m/s, and more if twisted rather than braided. So meta-aramide strings can be worth trying. If needing an impregnation, natural rubber is the elastomer with smallest losses. Tennis rackets and other sport goods need strings with similar qualities as music instruments. Meta-aramide may improve them. Marc Schaefer, aka Enthalpy

Usual wolf killers seem to use banal elastomers between the string and a metal mass, so they would dampen all frequencies, their relative effect being best felt at the strongest resonance. Schleske's damper is allegedly tuned, and his measured response curves support the claim. He doesn't tell on his website how the damper is built despite having sold several, secretive thing. Just elastomer and a mass is conceivable, but for a stable resonant frequency, I'd prefer an all-metal design which looks easy at 100Hz using small parts in flexural mode. Strings vibrate between the bridge and the holder. They shall not resonate there and get some damping organic wrap from the manufacturer, but they receive movement from the speaking part of the string, over the bridge sitting on the table and the bottom, whose stiffness is limited as they shall vibrate. Some violin workshops even let musicians pay to remove the damping material from the strings there. This changes the sound, and some customers even believe it improves. ========== Erratum to the figures in my message of February 14, 2019 03:09 AM. Was Now ------------------------ 50mm 36mm (drawing) 14mm 22mm (drawing) ------------------------ 20mm 10mm 6.0kN/m 12kN/m 4.4kN/m 10.8kN/m 50mm 36mm 14mm 22mm 4.0kN/m 10.3kN/m ------------------------

Luis & Clark manufacture graphite fibre cellos and other instruments luisandclark.com as do some competitors. One amazing record by Scott Crowley 5SRDj9xGAoM on Youtube the détaché starts quickly and neatly, without the noises so common with celli. The musician and the strings matter a lot, but the instrument too. The timbre is extremely clear. This strikes me less at a cello, which I don't play, as wooden instruments too have quite a clear sound. The timbre is also hollow. Most musicians owning a graphite cello comment "useful under temperature contrasts" or "sturdy and easy, nice for students" but "won't give up my wooden instrument". Records of (carbon) graphite fibre violins exist too on Youtube, and they sound just like one expects: badly clear, hollow, with very uneven intensity. No, thanks. From manufacturing videos, the body is just a couple layers of fabric. Then graphite can't compete with wood, as explained here on December 30, 2018. To the very least, it would need a sandwich, for instance with a balsa core, to achieve a decent velocity for flexural waves. Copying a violin's dimensions with an isotropic fabric isn't reasonable neither. Hi StringJunky, thanks for your interest! This works. Several ways exist to kill the wolf tone, with varying selectivity. Some instruments exhibit the instability over 3-4 semitones, which prevents tuning the offending frequency between two semitones. Then you have the worry of unusual tunings (for baroque music, or to play with some historic or detuned instrument), of glissando, portamento... A more selective approach puts an extra mass at the best place on the table. It's also a shift of the offending frequency, but it doesn't affect all the notes. The more common approach puts a damper on the string, between the bridge and the string holder, where the string isn't supposed to resonate. This one reduces the resonance instead of shifting its frequency. But it acts on all notes. Martin Schleske claims to taylor a resonator that dampens only the instrument's offending resonance schleske.de/en his curves support the claim. This would be the best targeted intervention, working for all tunings and leaving intact the rest of the response. The setup I propose is more for research than for an actual instrument. It aims to reproduce my claimed mode split without using a resonance, so if a wolf tone is observed, this will favour my explanation. Or disprove it.

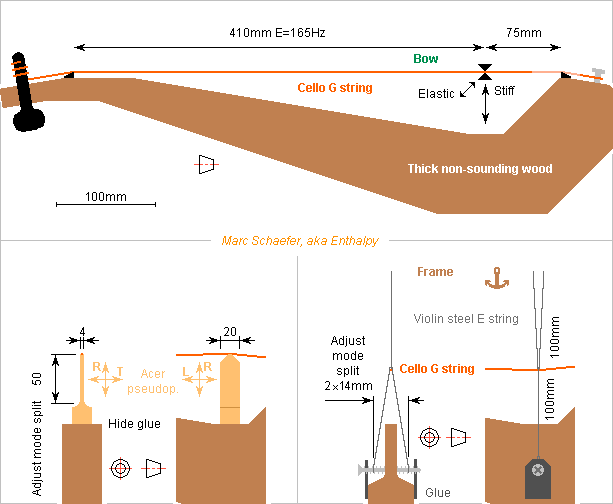
To check the explanation I proposed for the wolf tone, the experimental setup could look like this. At left a bridge is flexible laterally, at right it's a steel string. Here at least the vertical modes of the string are harmonic thanks to the boundary conditions and the uniform lineic mass. Horizontal compliance lowers the string's horizontal mode by adjustable 4Hz from E=165Hz. This results from the equivalent of 20mm extra length, that is horizontal 6.0kN/m side stiffness of the imperfect node. The string's non-speaking length keeps its damping yarn and it can be 75mm to have no common low harmonic with the speaking length (I checked only the vertical modes). The stiffness of these 75mm with 120N string tension leaves horizontal 4.4kN/m obtained from the tweaked bridges. 1mm is the maximum lateral deviation of the non-speaking length of the string at the tweaked bridges. ========== The flexible wooden part (left on the sketch) uses stiff glue. Mind the wood's orientation. The height of the thin section adjusts the frequency drop of the string's horizontal mode. At right on the sketch, a violin E string of 0.25mm unspun steel serves as a pseudo-bridge. Some 12.6N tension would resonate the 100mm at 902Hz to avoid common harmonics with the cello string, but more tension may be better, and additional reasonable damping looks useful. The violin string is bent sharp pemanently. The mere tension of the four 100mm sections brings 0.5kN/m horizontal stiffness, and the adjustable 2*14mm width of the Lambda shape 4.0kN/m more. A reasonably sturdy wooden frame, not displayed on the sketch, holds the upper V made of violin string. ========== If a wold tone appears in this setup with no soundbox resonance, it will favour my explanation. Many cello strings are ferromagnetic, useful to excite each mode separately. A repetition rate of the wolf tone near the frequency difference between the modes would be a further argument. Both variants of the setup let adjust the frequency difference. Marc Schaefer, aka Enthalpy

The wolf tone is a sound instability that can appear on celli and double basses, rarely on violins de.wikipedia (audio) en.wikipedia - schleske.de/de - schleske.de/en theories exist, essentially a strong body resonance that couples too much with the string. These theories match some observations but fit others imperfectly. A string can and does vibrate in any perpendicular direction, plus all the combinations, which includes elliptic modes. If the bridge is stiff, all modes have the same frequency. But if the soundbox resonates strongly, the bridge is more mobile, which lowers the string's frequency, and more so in one direction decided by the soundbox' behaviour. The string modes split in two that have different frequencies and can beat. The split may be more common at celli and double basses because their bridge is tall and narrow, so body resonances matter more to the string in the transverse direction. I suggest to inject this mode split in the current theories. Some experimental checks: If the wolf tone persists when a single string remains on the instrument, try unusual bowing directions, observe if they have an influence. Will that be convincing? On a hauling cello, use a capodastro, check by an actuator if the string has split modes and if their frequency difference matches the beat when bowing. Build a pseudo-instrument with a string but no soundbox, where the bridge is stiff in one direction but flexible in the other, for instance steel wire in V shape, or flat wood aligned with the string, preferably at 45° with the bow. Check if the wolf tone appears with the mode split but without any body resonance. Measure both modes, check if the instability's frequency is the difference of them. Pluck the string, compare with the bow. Marc Schaefer, aka Enthalpy

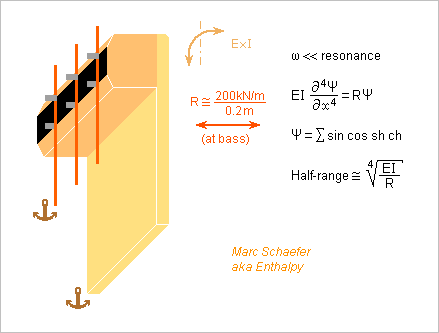
Estimated bridge stiffness required by my two harp designs with vertical soundboard. From the previous message, the bass strings should feel about 200kN/m, and if the bridge is to spread the side movements over +-0.1m, R~1MN/m2. The bridge must be stiff enough for that: EI~100N*m2. Beech (E=12GPa) needs W=e=18mm. If it sounds decently, 1D graphite (170GPa) on wood needs e=1+12+1mm W=7mm, a bit lighter. Medium and trebles need different dimensions. ========== At its column end, the bridge could be anchored with elasticity so the lowest strings feel a good stiffness and move the soundboard at the higher strings too. The unstressed soundboard can hold at its top ridge under the bass strings, and be free at the bottom. ========== Imagine that the narrow tall soundbox contains 0.03m3=210nF with the unstressed soundboard. The lowest H2 has 62Hz and we don't hear fundamentals lower. For arbitrary 1Parms in the box, the power radiated by the small source is 0.15µW while conduction to 0.6m2 box wastes 0.03µW, so it's big enough for that. Air elasticity pushing on equivalent 0.2m2 at the bass bridge portion adds 200kN/m stiffness, the full stiffness goal, so the box could be slightly bigger or the soundboard smaller. If the equipped soundboard brings 150g equivalent inertia and the bass strings too, air elasticity resonates them near 130Hz. Fluffy material in the box can dampen this resonance. My designs have leaks around the soundboard, say 1mm*1.6m wide and 15mm long. At 62Hz and for 1Parms in the box, inertia limits them to 0.14m/s and 0.2dm3/s compared with radiated 0.08dm3/s. The leak intensity improves with the frequency squared and the box volume, and it's nearly in phase quadrature anyway, resembling more a Helmholtz resonance around 100Hz, combining with the previous 130Hz to make 160Hz. The leaks waste power by viscosity. For 1Parms at 62Hz hence 0.14m/s it's 16µW. This reduces the strings' decay time. The box volume improves this loss, holding the soundboard where possible too. Frequency improves all this quickly. At 140Hz, radiation equals viscous losses. Marc Schaefer, aka Enthalpy

The soundboard of the usual concert harp, 8 to 10mm thin (my mistake) and 580mm wide, can't resist alone the traction of the low strings. The midrib (=bridge at present harps) does it there by holding at the pillar, but this makes the soundboard very stiff under the bass strings. The bass strings also resonate longer than needed, so a more compliant soundboard could be louder. Imagine that the soundboard flexes by 0 to 10mm under the 15 lowest strings that pull each mean 500N, that's roughly 1.5MN/m, neglecting all angles. Badly stiff. ========== Tone wood isn't flexible at identical bending resistance. Accordingly, the luthier Camac replaced at least the lower end with an aluminium bar. Material Pedantly Resistance Young Merit --------------------------------------------------------- Spruce Picea abies 70 12 49 Sycamore Acer pseudopl. 95 10 93 Beech Fagus Sylvatica 115 12 103 Yew Taxus baccata 105 9 120 Aluminum AA7075 480 72 146 Titanium Ti-Al6V4 830 114 210 Steel NiCoMoTi 18-9-5 2000 190 471 --------------------------------------------------------- R MPa E GPa R^1.5/E Steel would give more flexibility than aluminium. This lowers the resonances consequently. Thickness, and optionally profile, that vary with the position, can increase the soundboard's flexibility only at its wide but underused lower end. Or if keeping wood, a wider thinner end of yew (it made longbows and mandolines) should outperform spruce and sycamore. Additional parts can resist the force and give more flexibility than a straight bar, for instance a transverse bar. The soundboard must be thin to accept the deformation. The midrib's end can pull the soundboard low until the strings pull it up. The position of the midrib's end can be adjustable, at the factory or while the musician tightens the strings. I'd have stops at the midrib's end to protect the soundboard. ========== Kurijn Buys made seducing proposals for the harp's soundboard: Kurijn Buys' report (in French) decouple the soundboard from the column, build it from composite materials to resist the string's pull but be flexible, prestress it, among others. ========== My two versions of vertical soundboard are far more flexible. Over 180mm for the same 15 lowest strings, spruce 3mm thick and 200mm high contributes only 2kN/m bending stiffness, and 40MPa allow 27mm deflection. If fastened 200mm lower, the 7500N cumulated tension contribute 38kN/m, whether this tension is in the string extra length or in the soundboard. This oriented compliance lets a string swing slower, but only in the transverse mode. For a string tightened with 770N, this acts like 20mm extra length over 1.27m or 0.8% pitch mismatch, so the beat half-period is 0.8s, shorter than the exponential decay time. Around 5* stiffer, or 200kN/m, would be better in this register: fasten the strings 40mm below the bridge rather than 200mm, or add wood springs at the bridge. The unstressed design needs abundant bracings for adequate resonances. +-45° orientations may protect the soundboard better against in-plane traction by the musician. The tensile soundboard has a big wave speed parallel to the strings. 14MPa tension and 400kg/m3 give it 190m/s, so a half-wave in 200mm height give a lowest resonance at 470Hz without bracings. Resonances need only bracings perpendicular to the strings. But since this soundboard moves like a flat sheet, its base concentrates the bending stress and may demand some protection. My two designs seem to have design margins everywhere, including for thicker soundboards. With a radiating area similar to the present harp, but movements about 7.5* bigger, my designs should be 17dB louder, as much as 50 present harps. Could that be a first step towards the gaffophone? fr.wiki and google Marc Schaefer, aka Enthalpy

Le Carrou used already a shallow chimney at one hole to indentify the Helmholtz resonance. How much would tall chimneys at harp holes bring? I take 100mm height at the holes Le Carrou measured. The narrower soundbox end isn't that deep, but it adds its own inductance. D131 (16.2H) // D120 (18.6H) // D111 (21.1H) // D89 (30.2H) = 5.1H which resonates the soundbox' volume at 154Hz, same as the soundboard at this harp model hence useless. This improves if doors shut some holes. 3mm elastomer are worth 2.2m air. The soundboard's compliance contributes too. With chimneys at the lowest holes (could be elsewhere), 2 holes resonate at 118Hz and 1 at 86Hz. Arbitrary 1Parms at 118Hz in the box would radiate 1.9µW, conduction would waste 0.1µW and viscosity >0.1µW, elastomer doors contribute, for Q<68. A rosace or narrow F-holes would increase the viscosity losses, as would leaving a single hole open with a shallower chimney. Fluffy material, as in loudspeakers, can dampen too strong resonances of the long air column in the almost-closed soundbox. Marc Schaefer, aka Enthalpy