Enthalpy

If one records the whole sound, transforms it by Fourier in the frequency domain and back in the time domain, it reconstitutes the record, up to minimizeable imperfections. But if one records only one or few pseudo-periods, the Fourier transform implicitly supposes that these represent a part of a periodic signal, which is the wrong start. In addition, a pseudo-period length must be cut very accurately, lest the step where the ends meet introduces high harmonics - and the limited sampling rate limits this adjustment.

Here are sounds with variable degree of distortion, and the source TutE.cpp to produce them. Distortion.7z All at 330Hz. The files Saw contain 15 harmonics like a sawtooth signal, Sine have only the fundamental. Mild is a very smooth deformation by a hyperbolic sine, while Hard is clipping. Beginning with none, the distortion increases in 2s intervals. Clipping removes the extreme 0%, 0.2%, 0.5% and 1% of the voltage in 2s intervals. It gets noticeable when 0.5% of a sine are removed, or 0.2% once you know what to listen at. The sound that has already harmonics is unaffected by 1% clipping. This distortion appears only when the amplifier saturates. Thanks to feedback, crossover in a class AB amplifier doesn't create such a distortion. Not even computer audio makes that much. Our ears detect around 0.2%, but only on a sine wave. Mild saturation reduces the gain very progressively at the extreme voltages: here it removes 0, 3%, 10% and 40% of the peaks before rescaling, in 2s intervals. This distortion, which introduces harmonics of lower rank, gets noticeable at 10% compression, wow, and on the sawtooth not even at 30%. Audio electronics doesn't create such a distortion, thanks to feedback. Loudspeakers would if extremely overdriven, but we aren't sensitive to that. So whether an audio amplifier shows 0.1% or 0.01% distortion is only marketing. As opposed, an electric guitar amplifier operates generally in saturation. Transistor end stages clip the wave while vacuum valves saturate more smoothly. I haven't heard the difference personally up to now, but based on the samples here, I easily believe that valves sound differently in a guitar amplifier. Well, we could just saturate the signal smoothly before sending it to a transistor amplifier. Marc Schaefer, aka Enthalpy ========== Hi JC, Swansont and the others, I come back soon!

What height difference do we perceive, and how accurate shall instruments be? Here are some favourable cases, where the same note is slightly raised between 1s-2s and between 3s-4s. Permil.7z The free 7-zip archiver expands the 7z format. If someone needs the bigger zip file, please tell me. www.7-zip.org The files Permil1, Permil2 and Permil5 raise the note by 0.1%, 0.2% and 0.5%. Those called Harm contain the harmonics 2, 3, 4, 6, 8 too. The height is a 440Hz A except for the files H2 (880Hz) and H4 (1760Hz). You may hear the height much better at the sounds with harmonics (at least I do). Is it because more Hz separate the harmonics? Probably not, since our height perception is closely logarithmic - in all cultures, from what is published. Anyway, I perceive the 0.2% raise better at 880Hz sine and even better at 1760Hz, almost as clearly as at the harmonic-rich 440Hz tone (whose harmonics 6 and 8 are weak). So a better height sensitivity to a fundamental or harmonics around 1760Hz would be a decent explanation within this limited experiment. How much? When I was young and played the violin, I could hear 0.1% at a 440Hz sine, now I need the harmonics, sob. The cent is also near our limit, reportedly; defined as 1/100 of a 1+0.059 half-tone, or 0.059%. Is it innate or trained? Rather both. Violinists switching for the first time to the alto have immediately an accurate height perception on the new notes, while on the cello it takes little time. And what about flautists who get used to their too low high G# and don't notice it any more? On the other hand, some violinists (...even very famous) don't hear the height well after decades of training. Some people, mostly violinists, claim to perceive the absolute height rather than intervals. From my experience, they don't tune by far as precisely as when referring to a standard. Also, a violin gives hints to the absolute height: its resonances differentiates the notes, and the strings sound more brilliant with more tension. So I formulate the hypothesis that these violonists are guided by their instrument - until I see or read further experiments. Our excellent perception of tone height makes the manufacture of instruments difficult: 0.5% (8 cent) detune would be bad, but for simple woodwinds, wavelengths predict the height to 10%, and the rest is professional knowledge. A known recipe for good woodwinds is that their harmonic resonances are aligned. Though, they play notes at least on two resonance modes, and the musician changes the embouchure between both, which modifies the reed's susceptance and the resonance's height http://www.scienceforums.net/topic/112039-woodwind-reed-susceptance/ so the good tune of the two octaves or twelfths can hamper the mode alignment. While I haven't seen that in books, I expect many instrument makers to know it. Marc Schaefer, aka Enthalpy

Wagnertuben (lower horns essentially) were ordered by ol' Richard for his operas. Bruckner and a handful more composers used them too. They would deserve wider use: nice sound, range not covered by similar instruments, and (I believe) available in many symphonic orchestras. Anyway, here are opportunities to hear them clearly: https://www.youtube.com/watch?v=mmLRtqGOAJk only music https://www.youtube.com/watch?v=Hifo18bVG80 some waffle (in German) https://www.youtube.com/watch?v=j-4xZD6BX_w begins 4:50, with some waffle (in German) https://www.youtube.com/watch?v=MFm2C-ve7qw 0:00 to 1:40 with waffle (in German) and from 6:23

Why? Air isn't dispersive at these frequencies under usual conditions. We write waves as Psi(t-x/c) which keeps the relative phases over the distance, or equivalently, keeps the signal shape. That is, if a harmonic crosses zero at Phi degrees after the fundamental does, one metre further it will still lag by Phi degrees. If changing only t or x/c, the phase turns more quickly for higher harmonics, but if following the sound propagation, at constant t-x/c, Phi keeps the same, and the signal shape too. That's observation rather than logic. Attempts to synthesize a musical sound from its harmonic spectrum, which can only produce a periodic signal, fail to imitate a musical sound. It's the very reason why present-day electric organs have samples of physical instruments in memory for each note and play these samples on the musician's demand. It's because other methods failed. I suggest to tinker with my piece of software. It lets adjust any harmonic at will to produce any periodic sound. Agreed. I must make some day the experiment of inverting one loudspeaker phase. It's said to be audible, but so many claims are unverified in Hi-Fi. My programme (TutD.zip in the first message here) only softens the attack and extinction of the notes because sudden amplitude changes are uncomfortable and distract the listener. Function WrWav, loops for (... envel *= DecRate) for (... envel /= DecRate) The envelope of a sound is very important to its character, agreed. But a long steady sound of a saxophone or flute can't be mistaken with a periodic signal. So the difference doesn't reduce to the envelope.

Many sources claim that when tuning a piano, the high octaves must be stretched out to sound in tune because the human ear perceives the intervals smaller there. So here are some intervals in the two last or the last octaves of a piano. The height of these sine signals is less clearly perceived, but harmonics would be unbearable. The notes follow the equally tempered scale, where the quart and quint intervals differ by 0.1% from 4/3 and 3/2. HighOctavesStretching.zip I hear these intervals in tune. No need to stretch the high octaves. Marc Schaefer, aka Enthalpy

Barry Stees put bassoon spectra on the Web (thank you!): http://steesbassoon.blogspot.de/2012/08/seeing-sound.html of which I pick the "good reed" graph of a C note (130.8Hz, mid-staff of bass key, a bassoon reaches an ninth lower) and misuse it as is for other notes, up to the oboe's high G. H | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 ======================================================================================== dB | -51 -38 -29 -24 -36 -38 -53 -52 -51 -53 -58 -59 -63 -59 -65 -61 -76 -69 -79 -87 -80 ======================================================================================== t (s) 0 1 2 *** 4 5 6 7 8 9 10 11 =================================================================== Note | C G C G C G C G C G Freq | 65.4 98 130.8 196 261.6 392 523.3 784 1047 1568 =================================================================== BassoonRaised.zip This synthesis from a harmonic spectrum, making a periodic signal, again suggests but can't imitate a musical sound. And here too, the timbre of the same spectrum depends on the pitch, becoming strident on high notes. -------------------- Now, in these high notes, I suppress the harmonics above a cutoff frequency. Note Cutoff =========================== 0s-1s | C 523Hz | none 1s-2s | C 523Hz | 6kHz 2s-3s | C 523Hz | 4kHz 3s-4s | C 523Hz | 3kHz --------------------------- 4s-5s | G 784Hz | 6kHz 5s-6s | G 784Hz | 4kHz 6s-7s | G 784Hz | 3kHz --------------------------- 7s-8s | C 1047Hz | 6kHz 8s-9s | C 1047Hz | 4kHz 9s-10s | C 1047Hz | 3kHz --------------------------- 10s-11s | G 1568Hz | 6kHz 11s-12s | G 1568Hz | 4kHz 12s-13s | G 1568Hz | 3kHz =========================== BassoonRaisedCutoff.zip Strident harmonics begin somewhere between 3kHz and 4kHz, independently of the fundamental frequency. That's also the highest note of most instrument families: I know only the celesta, glockenspiel and violin to exceed it. The varied cutoff frequencies often change just one or two harmonics. This bassoon spectrum, with amplitudes increasing to the 4th harmonic and decreasing slowly, is artificial and aggressive on high notes. Double reeds, with their wide spectrum, need a filtering air column more than single reeds and flutes do. This filtering eases the wider range of bass instruments; other causes are more direct. Marc Schaefer, aka Enthalpy

I've finally checked that I don't hear neither a fundamental at 10kHz, 12kHz, 15kHz with my setup. It results more from the loudspeakers and headphone than from my age (adults didn't hear the 15kHz hiss of TV sets when I was a teen) because one side cuts earlier than the other, and when I swap them it follows the headphone. So harmonics above 10kHz are unlikely perceived. My headphones resonate at 3500Hz, less around 250Hz, and they (and the ears) get weaker below. If the volume is set for 300Hz, 60Hz is nearly inaudible. The loudspeakers are again worse. -------------------- Here I tweak an oboe spectrum transposed to 220Hz: the same measures by Kendall Milar, played one octave lower, in the baritone oboe's range. Stronger harmonics 8 to 15 make the timbre richer and more open but not strident as at 440Hz, while weakening them produces a muffled tone. The harmonics 21 to 28 (6kHz) make now a tiny difference despite being 60dB below the strongest one, and if amplified to -55dB they make the sound strident. H | 1 2 3 4 5 6 7 | ============================================ Always | -37 -23 -20 -29 -39 -47 -44 (dB) ============================================ H | 8 9 10 11 12 13 14 15 | ============================================ 0s-1s | -38 -36 -40 -45 -49 -59 -55 -65 | (+10dB) 1s-2s | -48 -46 -50 -55 -59 -69 -65 -75 | Measured 2s-3s | -58 -56 -60 -65 -69 -79 -75 -85 | (-10dB) 3s-end | -48 -46 -50 -55 -59 -69 -65 -75 | Measured ============================================ H | 21 22 25 27 28 | ================================ 0s-4s | (nothing) | 4s-5s | -80 -80 -80 -80 -80 | Measured 5s-6s | -65 -65 -65 -65 -65 | (+15dB) 6s-7s | -55 -55 -55 -55 -55 | (+25dB) ================================ OboeLower220Hz.zip -------------------- Now the same oboe spectrum is transposed to 110Hz: two octaves lower, in the bassoon's range. Without harmonics 8 to 15 (0.9 to 1.7kHz) it sounds uncomplete. Their amplitude measured from the oboe doesn't suffice; adding 10dB makes a more normal sound, not at all strident like at 440Hz. The harmonics 21 to 28 (2.3 to 3.1kHz) matter a little bit at their measured amplitude. At -55dB, the sound is abnormal but not strident. Adding harmonics 30 to 90 (3.3 to 10kHz) at -65dB makes the strident sound; a credible sound needs the harmonics 21 to 28. H | 1 2 3 4 5 6 7 | ============================================ Always | -37 -23 -20 -29 -39 -47 -44 (dB) ============================================ H | 8 9 10 11 12 13 14 15 | ============================================ 0s-1s | (nothing) | 1s-2s | -48 -46 -50 -55 -59 -69 -65 -75 | Measured 2s-end | -38 -36 -40 -45 -49 -59 -55 -65 | (+10dB) ============================================ H | 21 22 25 27 28 | ================================ 0s-3s | (nothing) | 3s-4s | -80 -80 -80 -80 -80 | Measured 4s-5s | -55 -55 -55 -55 -55 | (+25dB) 5s-7s | -80 -80 -80 -80 -80 | Measured 7s-end | -65 -65 -65 -65 -65 | (+15dB) ================================ H | 30 40 51 63 76 90 | ==================================== 0s-6s | (nothing) | 6s-8s | -65 -65 -65 -65 -65 -65 | Arb ==================================== OboeLower110Hz.zip -------------------- So the frequency more than the rank makes unpleasant harmonics. Marc Schaefer, aka Enthalpy Hi everyone, I'm coming back soon!

PC hardware is always of bad quality. Price dominates everything. And since the signal comes from a PC hence is full of electric noises, I wouldn't invest in good headphones. That said, headphones are by nature far better than loudspeakers. Especially, the box size doesn't limit their band at low frequencies, nor do headphones show huge resonances. To synchronize with the fundamental the harmonics of varied phases, the headphones would need a strongly non-linear operation. Such a huge non-linearity would be noticed. Feel free to connect a Hi-Fi amplifier and loudspeakers to the PC, or to transfer the wav files to your Hi-Fi Cdrom reader, and check what you hear there. Mathematic? Mathematicians are highly welcome in this thread! Figures give strong evidence that the suppression of low harmonics has algebraic solutions, but as an old engineer, I didn't try longer than five minutes. Rational numbers and cosines don't mix so easily, 7th grade equations neither. My piece of soft does that, just with a few added bangs and whistles to change the amplitudes more conveniently. But a different experiment would be a welcome double-check of course.

I had wanted T=4n for bad reasons. T=2n suffices and enables new combinations. Improving slightly over Jan 22, 2018: T=374 gives weaker H3, H5, H7 with 11 transitions than T=344, while the bigger T=856 and T=1092 still outperform both. Still the dumb software, run up to T=1040. ================================================== T a b c d e H3 H5 H7 H1 ================================================== 374 14 32 34 42 46 -73 -91 -82 0.82 ================================================== ---------- I've tried 15 transitions to minimize H3, H5, H7 with T=2n. Only up to T=434, which less stupid software would relieve. 15357.cpp ====================================================== H3 H5 H7 H1 T a b c d e f g ====================================================== -75 -73 -72 0.55 222 4 12 18 31 35 49 51 -84 -81 -96 0.81 368 11 25 30 45 46 49 51 -80 -inf -inf 0.49 420 7 18 37 47 70 77 102 -100 -73 -75 432 11 30 32 33 41 76 80 ====================================================== Found no exact solution: only -81dBc with T=368. The number of trials is too small to squeeze three harmonics by chance. Marc Schaefer, aka Enthalpy

Kendall Milar published some oboe spectra (thank you!) https://ida.mtholyoke.edu/xmlui/bitstream/handle/10166/715/257.pdf of which I fed the fig. 23 (page 41/88 in the pdf) in my synthesis software: the spectrum of a 440Hz A, comparing wood with plastic bodies there. Elsewhere, that report compares the spectra among musicians, reeds, instruments. ---------- My soft synthesizes a periodic signal from a spectrum. This can vaguely suggest an oboe, a clarinet, a trumpet. It can't imitate a flute, a saxophone, a violin, even on a steady note. All combinations of harmonics amplitudes result in a dead, artificial, synthesizer-like sound. I tried - try it too to get convinced. A musical sound is by nature non-periodic, hence a harmonic spectrum doesn't represent it. Time to progress beyond Helmholtz hence. At least one group (university in Brittany) imitated a violin better with a non-periodic signal. Nevertheless, the harmonic spectrum contains some hints about sounds and instruments and is relatively simple. ---------- Even on a throat note (first octave A), this oboe has its harmonics 2, 3 and 4 stronger than the fundamental. I tried to make the fundamental 10dB stronger and weaker than the measure: H | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ====================================================================== 0s-2s | -27 (dB) 2s-4s | -37 -23 -20 -29 -39 -47 -44 -48 -46 -50 -55 -59 -69 -65 -75 4s-6s | -47 ====================================================================== OboeA440_Fund_10dB.zip The weak fundamental is part of the narrow, elegant oboe sound. ---------- Adding (2s-4s) the harmonics 21, 22, 25, 27, 28 at 60dB below the harmonic 3 makes no perceivable difference. They begin at 9kHz, where our ear is less sensitive but headphones hopefully not too bad. OboeA440_H21H28_60dB.zip ---------- In this comparison, the harmonics 8 to 15 are stronger (0s-2s) or weaker (4s-6s) than the measure: H | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ====================================================================== 0s-2s | (dB) -38 -36 -40 -45 -49 -59 -55 -65 2s-4s | -37 -23 -20 -29 -39 -47 -44 -48 -46 -50 -55 -59 -69 -65 -75 4s-6s | -58 -56 -60 -65 -69 -79 -75 -85 ====================================================================== OboeA440_H8H15_10dB.zip Damping these harmonics (>3.3kHz in this case) changes the sound from strident to rich to muffled. As far as a periodic signal lets tell, it's much of the difference between most double reed instruments, often with wider bore and tone holes, and an oboe. As my figures suggest https://www.scienceforums.net/topic/113115-intentional-losses-in-wind-instruments/?do=findComment&comment=1035629 the chambers at the oboe's tone holes contribute to this function very efficiently. Marc Schaefer, aka Enthalpy Hi Mathematic and JC, thanks for your interest! Replying soon.

Random noise is often stronger than the harmonics, yes. But in some uses, often with a narrow band, the harmonics dominate. Measuring very weak harmonics is not easy, I had already to invest some time in it. The and (or the xor) of two fast squares is, after removing the high frequencies, a triangle, full of harmonics. Making a product (call it heterodyne) of two approximate sines makes a better sine. But with squares, both third harmonics beat too and produce a third harmonic of the beat frequency.

Hello everybody and everyone! I'd like to share some thoughts about sound perception here. ========== First, does the phase of the harmonics matter in a periodic sound? This was a debated question when Hi-Fi was fashionable, and is still interesting. Here's a piece of software I made for more general purposes. It creates a file Tut.wav playable by Winamp, Windows' Sndrec32.exe, Media Player and probably more. The user defines a spectrum (hence of a periodic sound), the soft writes the sound in the file. TutD.zip I recommend to listen with headphones rather than PC loudspeakers that create misleading distortion even at low level. And this is a 440Hz sound with H1, H2 and H3 of equal amplitude, where the phase of H2 or H3 vary between two seconds intervals: 0s 2s 4s 6s 8s 10s 12s 14s 16s =========================================================== H1 (0dB) | 0° 0° 0° 0° 0° 0° 0° 0° H2 (0dB) | 0° 45° 90° 135° 180° 180° 180° 180° H3 (0dB) | 0° 0° 0° 0° 0° 0° 180° 45° =========================================================== H123Phase.zip And the net result is: I hear no difference at all. The phase of the harmonics does not matter. Marc Schaefer, aka Enthalpy

Hi Frank, At the temperature of the sunheat engine, you don't have to care about ionization, catalysts nor active dissociation. The state in the chamber results from the heat whatever you do before. You should sniff a milligram of ammonia (diluted in the air!) before considering tons. You'll change your mind. If really you want an antifreeze in water, consider guanidine and pimagedine (made on Earth), which produces only gas upon decomposition. ========== Test facility: concentrated sunlight on Earth can't reproduce simultaneously the power density and the convergence angle attained in space, but both are important to test the heater. As opposed, a test setup in a lab is small, decently cheap and quickly purchased, and works in cloudy Europe too. I didn't detail it here but have clear ideas and figures about it. Easy choice.

Hi JC and the others! The nice toy from Intersil is a digital filter. Digital processing achieves about any performance, but when you convert to an analogue signal, the DAC spoils the spectrum. -60dBc signal purity is common, -80dBc is rare, and for the -120dBc or -140dBc I needed in some applications, there is no other means than an analogue filter, with components chosen for linearity. Fortunately, my pure sine accepted a fixed frequency then, so the analogue filter was reasonably easy. "Only" a matter of isolation and clean routing for electromagnetic compatibility. But if the frequency must vary by more than a factor of 2 or 3, you have no fixed corner frequency where you can put a filter cutoff to separate the varying fundamental from the varying harmonics. One approach, seriously difficult, is to build a (very linear) filter whose corner frequency follows the wanted fundamental frequency. The other approach, for which I propose the waveforms here, is a means to create a fundamental that is free of the lower harmonics, so that a fixed filter removing the higher harmonics suffices. ========== Pure sine from a noise: if a filter has a very narrow bandwidth, its output resembles a sine over a limited duration. If you observe it over a longer time, the amplitude and phase of the pseudo-sine fluctuate. It's Heisenberg's energy-time uncertainty, call it bandwidth-time for electrical engineers. ========== The exercise: it's a matter of power, independent of the ohmic value, and the bandwidth decides rather than the carrier frequency. Your power is 0dBm, the 300K noise is -174dBm/Hz. So if you measure over a 15kHz=42dBHz bandwidth you detect (depending on the certainty you want) harmonics of -132dBm = -132dBc, over 1Hz bandwidth -174dBc, and so on. Now, if it's an audio signal, our ears don't hear such a purity, and the loudspeakers introduce more distortion than the amplifier. I had built inductive transmitter and receiver to locate a rocket on the ground. With 1Hz bandwidth (triple heterodyne, synchronous local oscillators, and more) around 457kHz I detected -172dBm. Radioastronomers use correlation receivers that integrate over hours, and their noise temperature is more like 20K.

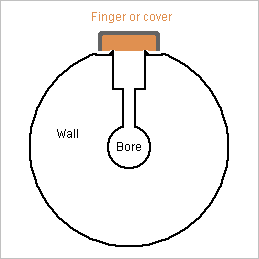
Dear musicians, scientists and everyone, here are some thoughts about the losses introduced on purpose in wind instruments. ========== To begin with, the chambers that the oboe has at its tone holes. I claim they serve to attenuate the high harmonics that are especially unpleasant on a double reed. I haven't seen up to now that thesis in books and research papers (which I haven't read all) but I suppose it is well known from oboe manufacturers. The oboe has quite a narrow bore, some 2mm at the top, and its tone holes are even narrower to soften the sound, as opposed to a flute or saxophone. Here I take 1mm wide holes where the bore has 4mm; having no oboe at hand, I can be badly off. A finger or cover could easily tap such a hole, but oboes have chambers where the tone hole is wider. I take 3mm width for the chamber, and 4mm+4mm height - unsafe guess. The closed tone hole builds a lossy Helmholtz resonator. The D=1mm L=4mm bore makes an inductor of 6.2kH and, at 4.5kHz, 3.0Mohm due to friction losses. The D=3mm L=4mm chamber makes a capacitor of 200fF and, at 4.5kHz, 15pS due to thermal losses. The finger or pad bring more losses, unaccounted here. The resonance is at 4.5kHz, nice to soften the sound. There, the Helmholtz shows 3.5MOhm to the bore. The wave impedance of the D=4mm bore is 34Mohm, so the lossy Helmholtz absorbs the unpleasant frequency. An oboe has several chambers that can cover a frequency range. A half-tone away from the resonance, the Helmholtz still shows 3.5MOhm +-j21MOhm to the bore, or 122MOhm losses in parallel. If the chambers are tuned one tone away from the other, they add the losses at mid-frequency, or 61Mohm, as compared with 34Mohm wave impedance. The set of chambers absorbs a continuous range that can span almost 2 octaves. That is, the set of chambers is perfect in this function. It's one of the missing features in the oboes with wide tone holes that Sax, Triebert and Gautrot tried to build. I suppose that the chambers serve also to tune the oboe. The inductance of the narrow holes lowers the pitch, but widening a D=1mm would be inaccurate, while shortening it by deepening the chamber is easy. A chamber as deep as the narrow part makes the lowest Helmholtz resonance, hence little sensitive to the chamber depth that adjusts the note's pitch. Marc Schaefer, aka Enthalpy

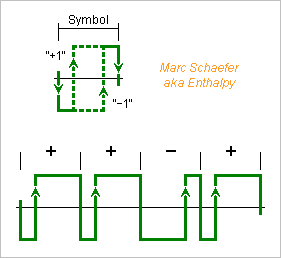
Rising and falling edges propagate with different delays to logic outputs, but here's a way to eliminate the consequences. Logic +1 and -1 states commonly decide outputs for the full duration of a symbol. An output symbol then begins with a rising or falling transition or none. Rising is done with a different delay than falling, which can be modelled by an added noise that has short peaks of duration tr-tf and amplitude +-2 at the transitions. This deterministic noise has a complicated pattern that adds unwanted harmonics to the output. I propose instead to have one rising and one falling transitions in each output symbol, and let the position of one transition, for instance the rising one on the sketch, represent the symbol's logic state. I haven't seen this before, but didn't check neither. Taking as a time reference the (here rising) edge that represents the logic +1: The position of the edge representing the logic -1 is at a time interval that does not depend on tr-tf. Only the smaller clock jitter has still an effect. The position of the (here falling) other edge is shifted by tr-tf, but this happens once per symbol independently of representing +1 or -1, so it adds a noise at the period of the symbols. Being independent of the represented sequence, it adds no unwanted harmonics. Using such symbols, we don't need any more flip-flops much faster than the analog output, which can now exceed the audio frequencies with good purity. The clock must be faster to define the positions of the (here rising) edges within a symbol, for instance 4* faster if the rising edges are at 1/4 and 3/4 of the symbol duration, but if a sequence has 180 symbols as does one described here above, the clock is only 720* faster than the analog output. This symbol representation has uses beyond the synthesis of harmonic-free sine. Notably, sigma-delta circuits can benefit from it: DAC, ADC (mind the stability) and power audio amplifiers. Marc Schaefer, aka Enthalpy

To estimate reed susceptances, I took a pressure and a displacement a priori. Both are imprecise, the estimation is worse. Measuring the pressure oscillation and the reed's movement under the same conditions would be better. More simply, we can load the reed with a known inductance and measure the oscillation frequency. If the volume of the chosen inductor is small, much capacitance comes from the reed, whose susceptance is accurately measured. ========== For a bassoon reed, I estimated here above a capacitance of 33pF at low notes, equivalent to 4.7cm3 air. The naked reed has a near-cylindric part where it fits on the bocal, whose approximately L=20mm ID=4mm contain only 0.25cm3. The wider tip of the reed contains some 0.15cm3. The reed's capacitance is the major contribution and remains important with a stiff embouchure that produces higher notes (more than an octave higher on a naked bassoon reed). A naked reed lets measure the susceptance on the whole range, including at some points to help analyze or design an instrument: play the reed on the instrument and alone with the same embouchure. The inductance must be modelled to deduce the capacitance from the frequency. The reed's cone is deduced from the reamer. Or a short narrow tube of accurate machined dimensions can fit the reed. L=0.1m ID=4mm would make 10kH that resonate the capacitance at 300Hz to 800Hz, in the instrument's range. About 1/3 of the tube's 1.3cm3 add to the reed's capacitance - or model that better or use a shorter narrower tube at 600Hz, since 100mm are 0.23*lambda there. Flow and thermal losses make only Q~10 at 300Hz. A few tubes let check that the model is sensible. I have nothing here to make the experiment, alas. ========== An oboe reed is said to be W=5mm h~1.3mm and vibrate over 10mm, swinging by +-7.4mm3 at low notes from +-5kPa (all vague estimates). The resulting 1.5pF act as 0.21cm3 more. An added tube of L=30mm ID=1.2mm would bring 32kH to resonate at 0.7 to some 2.2kHz. It would give only Q~5 at low notes but is already 0.19*lambda long at high notes, so several tubes would improve. ========== A reed for soprano clarinet is 13mm wide, a known mouthpiece opens by 1.15mm over 20mm length, but the musician reduces that: I take 15mm and 0.65mm for low notes. If peak 5kPa close the reed, the reed's capacitance is 8.5pF, as much as 1.2cm3 air more. The mouthpiece contains over 10cm3 air, hampering a measure as is. Shortening holes wouldn't bring enough. Instead, we can put a tube of ID=3mm L=80mm in the mouthpiece and fill the rest with modelling clay. A pyramidal void in clay, W=10mm L=20mm h=5mm over the reed around the tube's end, adds 0.3cm3 which must be measured. Then, 14kH by the tube let resonate at 420 to maybe 800Hz, in the instrument's range. Q~9 at 420Hz, L~0.18*lambda at 800Hz, so the tube isn't just an inductor. Two tubes would improve. Bass clarinets and low saxophones make it easier. Marc Schaefer, aka Enthalpy

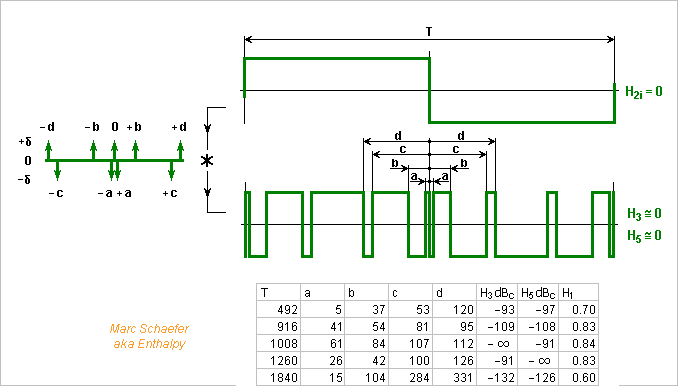
I've let the dumb program combine eleven transitions to minimize the harmonics 3, 5 and 7. Search11357.zip Up to T=1220, no exact solution was found, not even excellent ones, but better than a DAC: -87dBc. 1006 choices are too little to squeeze three harmonics by chance. ================================================== T a b c d e H3 H5 H7 H7 ================================================== 344 14 37 43 75 76 -71 -72 -78 0.75 980 17 58 81 152 159 -105 -80 -86 0.79 1092 41 106 122 171 173 -95 -87 -87 0.81 ================================================== Marc Schaefer, aka Enthalpy Thanks for you interest! I give in the first message estimations of the distortions introduced by the gates. I did realize and measure that one, and the observations fit the estimations. We're speaking of harmonics at -120dBc here, which isn't common. While I have already produced a spectral purity of -143dBc by an analogue filter, this was at a fixed frequency. If the fundamental were to vary by a factor-of two or more, I wouldn't like to design and build a tracking filter with such a performance.

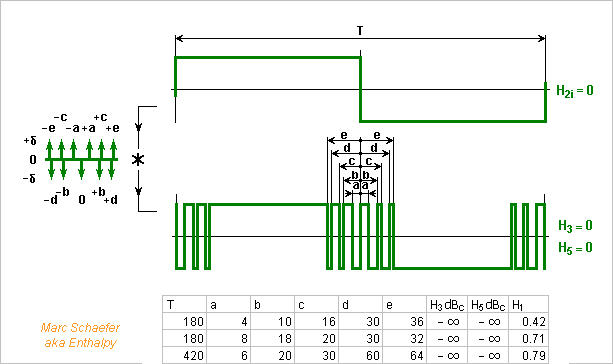
One algebraic pseudo-proof of H3=H5=0 would write the cos(a*2pi/T) and others as polynoms of cos(2pi/T) and check that the sum is zero. This path is inaccessible to hand computation. Even the waveform with T=180 needs e=32 where the contribution to H5 is a polynom of degree 32*5=160 of cos(2pi/T) that has all even coefficients. Software could do this computation exactly using ratios of integer numbers. I call it pseudo-proof because humans can't check the computation. They can only prove the algorithm and hope that the program, compiler, runtime libraries , OS, hardware... make no mistake. Alone the expression of cos160(2pi/T) has coefficients like (16080) that take almost 160bits to write, so the program or library must compute on rational numbers with arbitrary precision.

Bingo with eleven transitions per half-period: three waveforms contain no third nor fifth harmonic to the computer's precision, with periods of 180, 180 and 420 clock ticks only. Very probably algebraic solutions, if someone proves it. Up to some 1000 ticks per period, the software finds only exact multiples of these three waveforms, including at their common multiple of 1260 ticks. Search1135.zip The former diagram suggestions save more gates here. The circuit fits nicely in programmable logic. Marc Schaefer, aka Enthalpy

Nine transitions per half-period reduce the clock frequency further: 1840 ticks per period, that's 36MHz for 20kHz, and keep H3 and H5 at 132dB and 126dB below H1. Some solutions are exact (very probably) for one harmonic, but none is for both harmonics, up to 2500 ticks per period. Found again by software that exhausts the computer more than the programmer's imagination. Search935.zip The counter could go up for a quarter period of the output signal, down for the next quarter period, and again for the next half-period. That would use the same Nands four times per period, reducing their number. Send the adequate Nands Or'ed to the output flip-flop as previously. With an integer number of ticks per quarter-period, such a counter must stay at the extreme values for two ticks, for instance with an extra flip-flop. Other period lengths and transition positions should spare that. No diagram, sorry. Marc Schaefer, aka Enthalpy

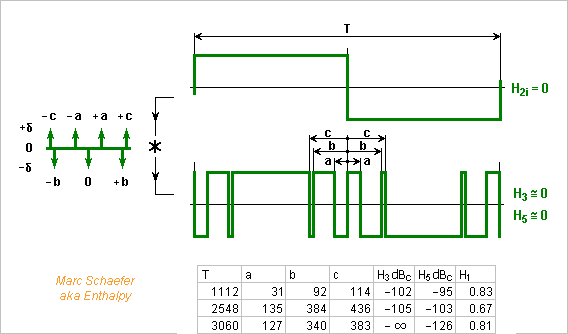
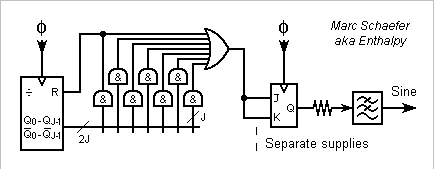
Adjusting continuously two transition positions lets suppress two harmonics, but positions approximated by a counter need a fast clock. Here, I propose to use 7 transitions and a slower clock. 7 transitions per fundamental half-period have shown no solution exact for both harmonics, but the number of positions combinations lets chance provide some good ones. This time, I let software make an exhaustive search: number of clock ticks per fundamental period, positions of the transitions. Dumb programmer but fast computer. Search735.zip 3060 ticks per output period need a 60MHz clock for 20kHz: 74AC counters and pipelined logic achieve it, an Epld is more compact. The waveform squeezes H5 to 126dB below H1, and H3 to nothing. The residual amplitude around 10-16 fits the computer's inaccuracy and chance can't decently explain it, so it must be an algebraic solution for this harmonic. This diagram is simpler. A toggle flip-flop reuses the logic for both output half-periods, increasingly useful with more transitions. The main counter has one bit less. Marc Schaefer, aka Enthalpy

Here are two records of oboes made of Pmma by a known luthier. Pmma is polymethyl methacrylate, like Plexiglas, Altuglas and more https://en.wikipedia.org/wiki/Poly(methyl_methacrylate) https://www.youtube.com/watch?v=NrJy8tNlBuQ music begins at 1:26, check especially the low notes at 1:55. That same musician played other instruments on the same day with the same reed, the trials are available on the same site - so only the instrument is to blame. https://www.youtube.com/watch?v=8AJnQk3ECYE music begins at 0:38. The low notes are again the worst. Two different musicians obtain the same sound, which is also how you expect a plastic to sound. It strikes even through computer loudspeakers. In short: inadequate material. Now I believe more easily that the material makes the difference between grenadilla and cocobolo oboes (Nov 07, 2017 here). And while an oboe must be more sensitive to the walls' behaviour, I believe more easily the clarinettists' comments against plastic. ========== Can the elliptic resonance explain it? Take E~2.5GPa and rho~1200kg/m3 for Pmma. The body widens to D~40mm at the low notes, and I take 5mm thickness, so (Nov 13, 2017 here) the first resonance for a cylinder would be around 3.3KHz, which is both our ear's maximum sensitivity and within strong harmonics of the oboe, like the 11th for low D. Most baroque oboes had rings at the bell, where locally thicker wood stiffened the wall. Their wood was more flexible than grenadilla. This may apply to plastics too. PC (polycarbonate) is less stiff than Pmma but it damps the resonances. Possibly a less bad material than Pmma - more factors matter. And polyketone, known for silent gears, could be worth trying. ========== Tárogatók are already made of boxwood (Buxus sempervirens), probably by tradition, and because wide grenadilla would be too expensive if available. Modern bassoons use even the flexible maple (with a thick moisture liner) instead of grenadilla or rosewood a century ago. They would be prime candidates for polyketone. I've seen no formulation loaded with short graphite fibres, but maybe plastic injection companies can do it if not the suppliers. And when long graphite fibers are wound to make axisymmetric parts, they are first impregnated by some resin: is molten polyketone feasible? Marc Schaefer, aka Enthalpy

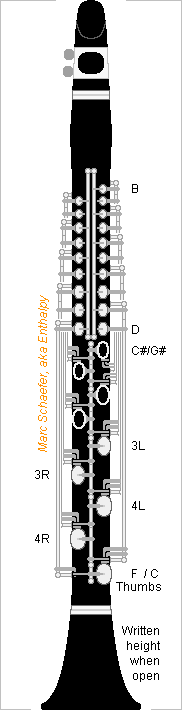
Here's a possible aspect of the clarinet with the automatic cross-fingerings proposed on Jan 07, 2018. Uncomplete, as the trill keys, register keys, and transmissions to the thumbs are not displayed, buttons for the ring fingers and pinkies neither. Most consequent holes are doubled, because a position can be opened by a closed-to-open transition of the finger holes with one mode key or by the next closed-to-open transition with the other mode key, and separate covers do that. Pairs of consequent holes that react the same way to the finger holes (but respond to different mode keys) use here long concentric shafts reaching the finger holes. A consequent cover is open at rest but often closed: When the lower of its controlling finger holes is closed, pushing directly. When the higher is open, so its rest spatula pushes down. When the proper mode key pushes on the consequent cover. As a variant, if the long shafts act indirectly on the consequent covers, only half as many shafts are necessary: five single or 2.5 concentric pairs per side. The same logical function of finger holes, carried by one shaft, can then close two consequent covers. More springs and corks in series, fewer long shafts. Alternating the hands chromatically eases the hole-open-or-next-closed operation. Both hands are but higher than the right one on a Boehm clarinet. The mode keys use four shafts, superimposed by pairs hence not all displayed on the sketch. Each mode key acts on consequent covers of both sides, and has right and left shafts for that. I don't detail the transmission from the thumbs; the buttons can optionally be split in right and left too, for simultaneous use, easing the adjustments. Usual Eb clarinets have one joint for both hands, useful here. As on some Ab clarinets, no separate barrel on this sketch: this eases a register hole there, but a reamer alone won't make the bore. As far as I understand the instrument at the Library of Congress from the picture http://memory.loc.gov/diglib/ihas/loc.music.dcmflute.1244/default.html it works differently from the system I describe. But there are strong similarities. The system for conical reed instruments would resemble much. Marc Schaefer, aka Enthalpy