Elen Sila

http://en.wikipedia....Volcanism_on_Io Would it be possible, through a combination of tidal heating, radioactive isotope decay, and the greenhouse effect, for a very large moon (like Titan) of a very distant planet (like Uranus or Neptune), to sustain earth-like temperatures and atmospheric pressure, as well as liquid water? How far out from the sun would this become infeasible? And, if feasible, how long could such a state exist, if sustained by an orbital resonance, as is the case with Io? A few million years? Billions?

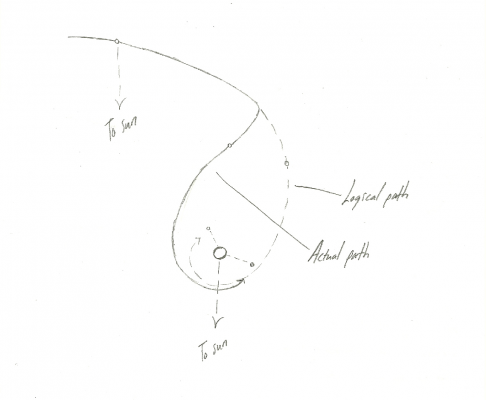
I'm aware that my conclusions are wrong. I am asking for an explanation of why they are wrong. Here were my two questions, originally, which I admit I did not enunciate very clearly. 1. Why do proto-planetary discs form in a prograde, rather than a retrograde, direction? 2. Once a prograde moon system has formed, why don't all of the moons fall into the planet due to head-on collisions with dust and rocks? My understand of your initial response, in terms of its practical application, is that objects being gravitationally captured do not follow the simple curves I described in my diagram, but rather perform a sort of "zig-zag" manoeuvre, where their motion relative to the planet reverses direction as they approach, due to some switch involving kinetic and potential energy that I don't really understand. Far moons would thus generally be hit in the face, dropping them in orbit, while near moons would generally be hit from behind, raising them in orbit, and resulting in the equilibrium you described. Is this a correct description of the mechanism of gravitational capture? Here's my attempt at a diagram. It shows the actual path of captured objects, as described in this thread, in a bold line, and and the logical path of captured objects, as described in my diagram, in a dotted line. If this diagram accurately expresses the system you've described, why does it work that way? What causes the reversal of direction?

They don't all have to be, they just have to mostly be. Since head-on collisions would be statistically more common, the moon would have a net loss of angular momentum. Our moon is a poor example, because it's so far out, and its orbital velocity is so low compared to the earth's (1.023 KPS versus 29.785 KPS), that it's actually usually moving approximately parallel to the earth around the sun, regardless of which way it's facing relative to the earth. Thus, it gets peppered on all sides roughly evenly. A better example would be, say, Jupiter's moon Io (17.334 KPS), or Saturn's moon Mimas (14.323 KPS), which both move around their primaries faster than they move about the sun (13.068 KPS for Jupiter, and 9.689 KPS for Saturn).

Why don't the moons always fall into the planet, as they lose kinetic energy to head-on collisions with dust particles, micrometeors, and asteroids? Is it because the angular momentum they steal from their primary's rotation makes up for it? Shouldn't one force or the other dominate the interaction, causing all moons to either break up or fly off, given enough time?

For reference, when I say "in the same frame", I mean "perceiving time at the same rate", as measured using the signal-timing method I described before in this thread.

No, I've totally heard of scientists creaming their pants over binary asteroids or double-dwarf-planet systems like Pluto and Charon. ... Yes we can know the masses of exoplanets. We just measure the back-and-forth motion of the star. How long it takes to move back and forth tells us the orbital period; and how much it moves back and forth tells us the mass. But wouldn't that just tell you the combined mass, as per g(m₁+m₂)/r²? Why would that tell you the ratio between the masses, as well, as I've often heard it's supposed to? OR WAIT. Of course you'd be able to tell the ratio between the masses! You'd be able to see the motion of both of them around the common center of mass; and then you'd just measure the ratio of their distances to the center of mass. Gosh, I'm dumb sometimes. Alright. I see what you're saying. Confusion cleared up.

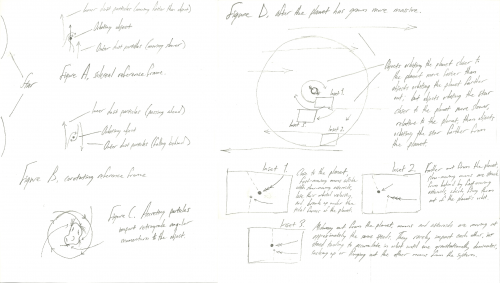
During the infancy of a planetary system, it usually consists of a young star, surrounded by a disc of spinning gas and dust. Eventually, turbulence in the disc results in the accumulation of clumps of matter, which over time grow into massive objects, which can eventually become planets, if they become so great as to achieve hydrostatic equilibrium and clear their orbits. Now, early on, before the planetlets have come into their own as rulers of a Hill sphere, the matter passing by them in adjacent orbits would be travelling faster if closer to the primary, and slower if farther out; thus, from a corotating reference frame, outer dust particles should be moving backwards, and inner dust particles should be speeding ahead. So, logically, per the diagram below, matter should, as it is accreting to the orbiting object, be imparting retrograde angular momentum to the object. Then, after the orbiting object has grown to the mass of a full-fledged planet, collisions and interactions with passing asteroids should destroy or eject all moons from the system, except those orbiting at approximately a certain ideal distance from the primary. Thus, every planet should, 1, rotate retrograde, and 2, have only one or two large moons, both of which should, 3, orbit retrograde. So why are none of these three things true? (In case you can't read my handwriting, here's a transcript of the diagram.)

Oh, whoa. I just realized. For any given object in keplerian freefall, the semi-major axis of the orbital ellipse is the distance at which centrifugal force exactly equals gravitational force. And, by extension, the gravitational mass of a planet is exactly equal to the sum of the mean orbital distance and the square of the mean orbital velocity of any given satellite of negligible mass. v²/r=gm/r² gm=rv² As I understand it, astronomers really like it when they find two objects of comparable mass, orbiting each other, because somehow it helps them determine the mass of the system. I would think it would be more helpful to find an object with a negligibly small object orbiting it; why is this not preferrable?

So, 0.026758–64.7^2/192000=0.004955; at Sylvia's equator, then, the effective gravity would be only five millimeters per second per second? On the earth, (398600.4418*10^9)/6378137^2=9.798285 meters per second per second; but 9.798285–(6378137*pi*2/86164.1)^2/6378137=9.764370 meters per second. The value Wikipedia gives is 9.780327 meters per second per second. The difference is small; but I'm not understanding where it's coming from: 398600.4418 is known to be the standard gravitational parameter of the earth to a very small margin of error; and 6378137 is likewise known to be the equatorial circumference of the earth at sea level in meters to within a very small margin of error; yet I produced a somewhat large margin of error as my result, both with centrifugal force and without it. I don't get it.

Can you put yourself in the frame of an object that is accelerating gravitationally, through orbit? Wikipedia says that freefall is inherently inertial. "Objects in free-fall really do not accelerate, but rather the closer they get to an object such as the earth, the more the time scale becomes stretched due to spacetime distortion around the planetary object (this is gravity). An object in free-fall is in actuality inertial, but as it approaches the planetary object the time scale stretches at an accelerated rate, giving the appearance that it is accelerating towards the planetary object when, in fact, the falling body really isn't accelerating at all. This is why an accelerometer in free-fall doesn't register any acceleration; there isn't any. By contrast, in newtonian mechanics, gravity is assumed to be a force. This force draws objects having mass towards the center of any massive body."

Hmm. I just came up with another scenario. Let's say Sam and Mary are both in space stations, orbiting the earth at the same altitude; Sam is several degrees ahead of Mary. In this scenario, Sam and Mary are not travelling in the same direction linearly, in the galilean/newtonian sense; however, they are travelling in the same direction geodesicly, in the einsteinian sense (at least, based on my understanding of the geodesy of spacetime according to Einstein, which I'm willing to bet is probably even worse than my understanding of time dilation). It seems to me that, in the curvature of spacetime by the earth's mass, Mary is following directly in Sam's path, and therefore her experience of time relative to him ought to be the same as if they were both travelling in a straight line, one after the other. Are they in the same reference frame in this scenario? Or am I totally misinterpreting the concept of spacetime geodesy?

... Wow. I'm so used to Wikipedia giving me the radii that I didn't even realize I was looking at the diameter. I hate diameters so much. Radii are so much more useful and relevant. I keep 2pi saved to my calculator as a constant, and almost never use my calculator's Pi button. Yeah, I get 64.6 meters per second for the equatorial rotation speed, at an equatorial radius of 192 kilometers. The orbital period at that distance would be 16831 seconds, and the orbital velocity would be 71.7 meters per second. So I guess the rotation speed isn't greater than the orbital velocity, and no negative gravity would be present. I'd still like to know how to calculate centrifugal/centripetal force on a rotating gravitational body, though. For the record, when you say "centripetal (inward) force", are you referring to, for example, the force of the floor of a rotating space station against the feet of an astronaut standing in it? Also, when you say "orbiting body", do you mean "body in freefall" or "rotating body"? (6.67384*10^-11)*(1.478*10^19)/192000^2, sure enough, is 0.026758 meters per second per second. However, 192 kilometers is only the asteroid's widest equatorial radius. Its mean radius is 143 kilometers, and its polar radius is 116 kilometers. If we plug in the mean radius, we get a surface gravity of 0.048237 meters per second per second; and if we plug in the polar radius, we get a surface gravity of 0.073305 meters per second per second. If we reverse-figure from 0.0729 meters per second, keeping the stated mass, we get a radius of 116.322 kilometers. I'm guessing the article is using the polar surface gravity; and since the polar surface gravity wouldn't be subject to the same centrifugal concerns, they wouldn't even have to factor that in. I'd still like to know how to calculate Sylvia's equatorial surface gravity though, accounting for centrifugal force.

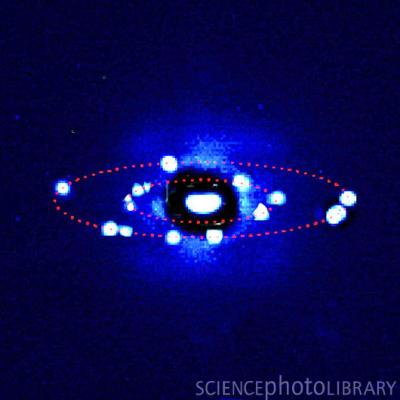
So there's this asteroid called Sylvia. (It's primarily known for having two moons, Remus and Romulus, but that's beside the point.) Sylvia rotates about once every 18661 seconds, sidereally; and her mean radius is about 286 kilometers. That means that, at her equator, assuming approximate sphericity (obviously a big assumption, but that's also beside the point), she rotates at about 96.3 meters per second. But, assuming an object of negligible mass could revolve around her at a non-eccentric distance of exactly her mean radius (again, implausible, but let's not get hung up on that), that object would have an orbital period of (286000^3/(1.478*10^19)/(6.67428*10^-11))^(1/2)*pi*2≈30598 seconds, and an orbital velocity of about 58.7 meters per second. If Sylvia's surface rotation speed is greater than her surface orbital velocity, shouldn't Sylvia have a negative surface gravity? If an astronaut wanted to land on her surface, wouldn't he have to use mountain climbing gear just to keep from flying off into space? Why does Wikipedia list Sylvia's surface gravity as 0.0729 meters per second per second, instead of accounting for centrifugal force in that figure? And does Wikipedia account for centrifugal force in its figure for the earth's gravity (9.780327 meters per second per second at sea level on the equator)? If so, why the inconsistency? Anyway, my main question is this. I know how to calculate surface gravity on a non-rotating object. But how do you calculate Sylvia's (or any other body's) actual surface gravity, accounting for centrifugal force? By extension, how would you measure the artificial gravity in a rotating space station, in meters per second per second? http://en.wikipedia...._%28asteroid%29 Pic related, it's Sylvia.

I'm not even sure. I do know this, though: if the earth suddenly disappeared, leaving Sam and Mary floating in space, Mary would go flying off into the distance way faster than Sam would. That, at least, shows that they do not have the same inertial rest frame.

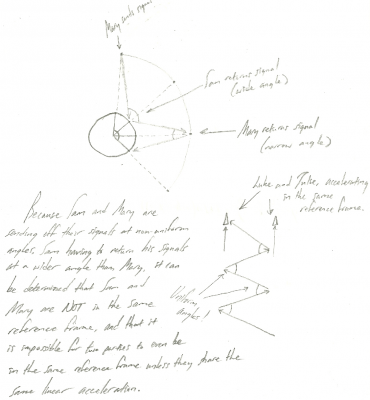
Alright. I suppose that makes sense. I still have a lot to learn, of course. But I guess my question appears fairly cleared up now. Also, while I was thinking about this scenario at school the other day, I came up with the following diagram, which actually kind of demonstrates that Mary and Sam must have a non-zero relative velocity. Let me know if this diagram is accurate, and really does have anything to do with the scenario and its solution. Again, in case you can't read my handwriting, it says, "Because Sam and Mary are sending off their signals at non-uniform angles, Sam having to return his signals at a wider angle than Mary, it can be determined that Sam and Mary are NOT in the same reference frame, and that it is impossible for two parties to even be in the same reference frame unless they share the same linear acceleration."