Atashi
Members-
Posts
5 -
Joined
-
Last visited
Profile Information
-
Favorite Area of Science
Physics
Atashi's Achievements

Lepton (1/13)
0
Reputation
-
Atashi started following Shape of Time
-
But, relative to what? To my understanding, Δtime its relative to Δposition and Δspeed. (v=d/t) Which in this case time is relative, and ever-growing in relation to position of the point, and the speed is constant: 1 unit/frame Unless if you meant the perception of time is relative between 2 objects, which wouldn't matter at all for my topic, since there is only 1 object represented by 1 point.
-
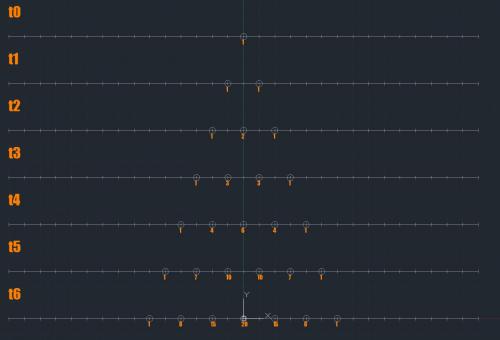
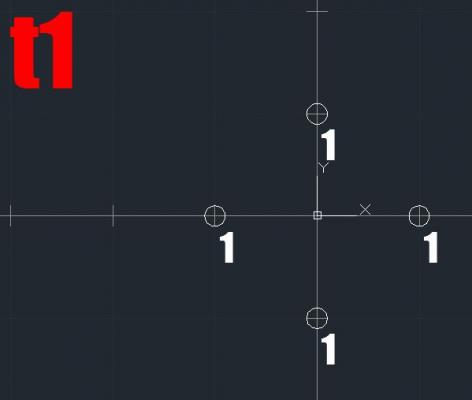
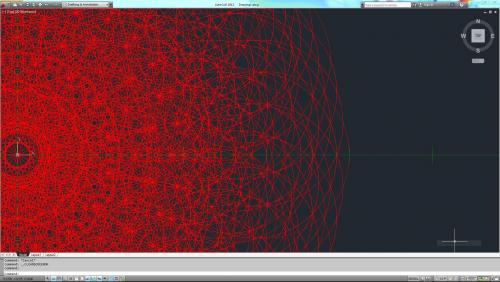
Revision 1. note* I've yet to find a program that satisfies me with its images, any suggestions? To understand this shape, accept that: "Time is measured by change. If there is no change; one can say that time has stopped." The amount of change that occurs can be acknowledgment of movement at any level or scale. To illustrate this, imagine an object(or particle)(represented by a point) in a 1-dimentional space(represented by a line). Now lets allow this object to move one unit it any direction, left or right, on this line, considering all the possibilities. Repeat the process considering both possibilities of the point at t2. As you will notice, the plot at 0 at t2 has been 'hit' twice. Thus the probability of the point existing at 0 at t2 would be higher than other locations. To calculate this, we take the point's 'density' and divide it by the sum of all the plot densities. density of p0 / sum of densities = probability 2/4 = 50% density of p3 / sum of all densities 1/4 = 25% Continue to do the same for t3, t4, t5... The distribution of the plots is equivalent to the values shown in Pascal's Triangle. Let's give this object a little more freedom and allow it to move in a slightly higher dimension By allowing it to move vertically. 1.1D maybe? To illustrate the probability more clearly, i have decided to assign a frequency of color to the plots according to their densities. The higher the density, the higher the frequency the point in space will be 'hit' Blue representing the highest density, and Red(with the lowest frequency) representing the lowest density. I have yet to be able to map this while allowing the point to move freely in 2d or 3d space. Any help would be greatly appreciated. The closest i am to getting anything is arraying arrays of 64 circles. Without the color representation of the density, this means nothing... Image of x=3 to x=4 at t6 I used arrays of circles because a circle represents all the possible movements of 1 unit in any direction Heres t5: t6: t10: For certain, i know the 0,0,0 in both 2d and 3d will have a density of infinity at t2. Thus resulting a possibility of ∞/∞ = 99.9*% These diagrams are fractals, a pattern that produces self replication. Fractals are common in nature, and time is definitely a part of nature. The acknowledgement of a reality is determined by where we are in time. Which reality is recognized is determined by what changes have occurred. And a probability is a fundamental property of reality. One can view points on the diagrams as many instances of "reality" varying in values of possibility. We currently live in a 3d space existing in the 4d axis known as time. Our 'view' of the 3d space is represented by a 2d cross-section of said space. So in an attempt to understand the concept of reality, Let's take xscections of our 3d model to gain understanding. <imagine image here> This colorful circle represents what reality is most likely for us to perceive. Take another crossection of this circle. <imagine image here> Would show a multi colored line showing different realities and their probability. If we took this and graphed it with Y=Probability X=Distance from 0 <imagine line-graph> Recognizing the values on such a graph would determine what reality is most probable and most comprehensible. With that said, could our brain be a tool which takes xsection images of 4d space to recognize 3d reality, Just as our eyes take xsection images of 3d space? Could the incorporation Chaos Theory into this using some kind of distortion factor be reasonable?
-
I've watched the series and i have to say that some of the data presented is rather mind boggling, but some ideas are just silly. I have to agree that megalithic structures with that kind of precision would prove difficult even with today's technology. (perfectly placing and perfectly cutting 3tonne blocks, 5 blocks per min) The transportation of the materials used when nothing else resembling that material is present. The similarities in design and ratio of the aztec and egytian pyramids are also quite "extraterrestrial"
-
Twin Paradox: Lets assume infinite space. Each twin is on a platform situated side by side to each other. In the original paradox, one twin(b) is propelled at near-lighspeed away from the other twin(a). As twin(a) you are stationary, and 50years has passed, twin(b) returns and has only aged 25 years. But when in reference you can also claim that: twin(b) was stationary, and twin(a) had been the one that left and return. as twin(b) you will have experienced waited 50years for twin(a)'s return. How can this be? In one world we have twin(a) aging twice as much at the time of reunion and in the other we have the opposite, though both events are one and the same. Perception determines reality exclusive only to the observer. but at the same time, as twin(a), you could state that twin(b) had been stationary. and upon your arrival after 25years, twin(b) would have aged 50. twin(a) would see an older twin(b) at 25years, and a younger twin(b) at 50years... Or would only 1 Reunion take place? If both had happened, would there be two differently aged twin(b)'s simultaneously? if this is possible, then twin(a) could also claim that both twin(a) and twin(b) were traveling at 1/2 the speed of light away from each other, bringing both of them back to the original location and both having aged the same amount. and any variation of that would be possible (90%vs10%, 80%vs20%...), and result in an infinite amount of twin(b)'s being produced. Let's step this experiment up. Now lets account for the 3rd observer twin©, or rather triplet, but lets not stress the details. twin© is put between twin(a) and twin(b) both twins will propel themselves from twin© at near-lightspeed, and return. twin© will will have aged 50years while twin(a) and twin(b) will return at the same time, both having aged 25years. What will this look like in the perspective of twin(a)? it would be impossible for twin(b) to have been going twice the speed of light. so would twin(b) and twin© both be traveling along side each other? If thats the case then would both twin(b) and twin© return having aged 25years during 50years of twin(a)'s time? Or would twin© have aged 25years while twin(b) having only aged 12?
-
I dont know where else to post my, sadly incomplete, theory so... (posted in psudoscience since i did no know what field of science it would go into) im looking for any input, and welcome all suggestions. I currently do not posses enough mathematical skill to provide anything for this, and help would be greatly appreciated. First, forget anything you know about time. To understand this shape, accept that: "Time is measured by change. If there is no change; one can say that time has stopped." In the diagram(s), each unit of time will hold one unit of change. "tn shows the distribution of the sum of all possibilities of the position of a point that has moved a single unit per frame of time through n frames of time" To do this, first assume a point in a 3 dimensional grid, this is time 0 (t0) For the sake of visualizing it more easily, lets start with a 2d grid instead. t1, put on a separate graph, we must consider all the possibilities of that point moving in any direction. The image will resemble a circle with a diameter of 2units. For t2, on a separate graph, generating a new image, we must consider all the possibilities of the points in t1 1unit in any direction. A circle, filled with infinite points, with a diameter of 4units emerges. Stop... Because some points on t2 are plotted more than once. what do we do? The density of the plot, will be refereed to as frequency: the number of times a point is plotted at the same point. To represent this, the highest frequency at points will be blue and the lowest will be red. Anything in between will fall into the spectrum accordingly. At t1, all the points reoccur only once. a white circle. "the halo". At t2, all the points on the very edge of the shape is plotted once. (red) All the points within have a frequency of 2. (green) And the center point has a frequency of infinity. (blue) resulting the 3 primary colors of light. *notice that there is no gradient yet, only 3 separated colors. At t3, all the points, including repeated points are taken into consideration. If a point has a frequency of 2, it will yield a circle with all the points containing the frequency of 2. I have yet been able to image the whole structure but i know that: There will be a red ring on the outer edge with a frequency of 1, There will be a blue circle, 2units in diameter, at the center with frequency infinity. These diagrams may also be added, and subtracted from one another. Though i would not know what adding would represent. By subtracting, we can view the distance moved = Tn+x - Tn These diagrams are fractals, a pattern that produces self replication. Fractals are common in nature, and time is definitely a part of nature. From these diagrams of time, we will see high frequency areas and low frequency areas These map out the existence of the point(at t0) at a certain point in time(tn). The position of this point is most likely to be in the blue regions, and less likely to be in the red. One can view a single point on this shape as "reality". The frequency of a point as being the probability of its manifestation in reality out of the total sum of frequencies of all plots of the graph of tn. The point frequency of 0,0,0 at t2 is infinity. Thus the possibility of reality of point 0,0,0 at t2 is ∞/∞ = 99.9*% This is already difficult enough to imagine on a 2d grid. What would it look like on a 3d grid? In continuation to the image presented, the 2d image is a cross-section of the 3d image along a line of symmetry. Mow, lets take a cross section of the 2d image and show it as a line graph. Y being the frequency, and X being the distance from 0,0 Then, imagine taking a cross-section of this line. The result will be dots at certain distances apart. Could this be how we perceive time? Acknowledgment of a certain value of a singular "reality"? When you take a xsection of a 3d object, youll see a 2d object, and points from a xsection of that. Similarly, when xsection of time(4d) would present you with our current dimention(3d), The xsection of that would provide a picture of reality(2d), The xsection of such would provide us with the "points" of reality. Is the incorporation Chaos Theory into this using some kind of distortion factor reasonable? I will try to post images as soon i get around to it.