BeuysVonTelekraft

How was the contact between human species during the evolution? Can you suggest me research sources about it?

Yay! You answered it! Thank you. So I just need to understand the implications of the axioms and theorems? Now it's kinda easier, I thought I ought to memorize.

Guys, what you think about: -For dummies books; -DeMYSTiFied books; -Complete idiots guide.

Ok, thanks for the advices. I kinda figured the way it should be done (tried?), Algebra, Calculus, then Analysis. I've got some books and I'm gonna start to read them. Thank you so much.

The course i'll make starts with Linear Algebra.

Hi, next year i'll start my bachelor's degree on mathematics, but i want to study something about it while i'm idle. I've found this: http://webdocs.registrar.fas.harvard.edu/courses/Mathematics.html And this: http://www.ufpe.br/proacad/images/cursos_ufpe/matematica_bacharelado_perfil_4904.pdf They're Syllabi from some mathematics courses, one of them is from the university near me, the other is from Harvard. Can someone suggest a study way? Where should I start and which books I should get? Thanks in advance.

From what I know until now - if i know something until now - the DNA can store information. But i've never read about how much information it is possible to store on it, any sugestion?

I am reading it here: http://www.amazon.com/Rubato-Composer-Music-Software-Component-Based/dp/3642001475

So, if there are lots of possible operations. How will i know what operation should i do?

I'm kinda doing what you're doing, i've been negligent with my classes while younger, now i want to build some projects that need the neglected content. I'm reading mathematics for the nonmathematician. It's a cool book if want some maths.

Oh, forget, i didn't undertand.

I guess the word is not "possible", the word is "known".

Can i say: Map it to n, instead of map it to {4,9}? And, where can i find all possible binary operations? I've searched a little but i can't find it.

I kinda modeled a monoid on Mathematica: I'm not very sure if i'm right on them. But what would happen in the case of the homomorphism of these monoids?

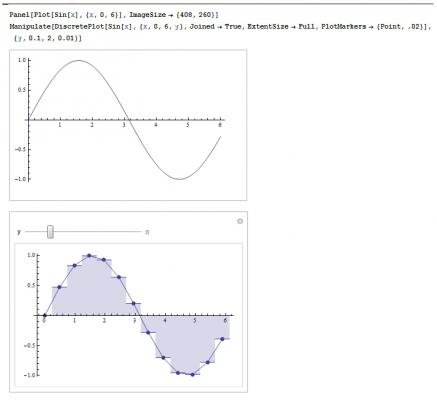
I'm reading Comprehensive Mathematics for Computer Scientists 1, has anyone read it? I've picked this book last year, i wanted to understand the Rubato music composer and after i understood what would be needed to operate it, i asked Guerino Mazzola about a good book to get started on the necessary topics, he suggested me this book. I opened the book and i made the first chapter pretty fast, but when the second chapter came, i swear that the only thing i could see is something like the image below. Now that i know a little more of maths due to books like "for dummies" and "The complete idiot's guide", i open the second chapter and it seems more like the image below: It's russian, it's easy.I can read it slow and stuttering, but i kinda understand it. I have a doubt on how it's reading should proceed. There are lots of axioms, remarks, proofs, sorites, etc. Should i memorize each one of them? What would be a effective way of reading it? Thanks in advance.

Yup, i understand it now, i even did a notebook on Mathematica for the case I need to explain it to someone in the future. The first image is a - theoretically - continuous signal, the second is the discrete signal and the y slider is the quantization level.

Got it. Now there's another concept on the book: Monoid Homomorphism. Given two monoids [Math] (M, *M)[/Math]and [Math] (N, *N)[/Math], a monoid homomorphism [Math]f : (M, *M) \rightarrow (N, *N)[/Math] is a map of sets [Math] f: M \rightarrow N[/Math] I understand the mapping, and the meaning of the monoid [Math] (M,*)[/Math], but i have no clue of the meaning of [Math](M, *M) [/Math]. The homomorphism, as the name suggests, seems to be making both sets having the same elements, am i right?

Yeah, yeah. I got it. I knew this process of audio conversion, i just didn't know this difference of continuous and discrete. Now it's perfectly clear to me, unless there are some other ill implications on the terms.

I wasn't envisioning something specific, i just thought that the natural structure of one object may allow only a finite level of variation on it's properties. I'm also not very sure if i understand what discrete and continuous means, i had a naive definition that, for example, a continuous signal would be a signal that could vary between [math]-\infty [/math] to [math]\infty [/math]. But i've read that when the continuous signal is captured and transformed into discrete signal, it's quantized. This made me think: On a quantized signal, you'll have intervals like 0 - 1, and if you capture say: 0.6 it's gonna be transformed in 1. Now i'm thinking that the continuous signal is the signal that, by not having a quantization, allow [math]\frac{y}{x}[/math] with [math]x[/math] being any number. On a discrete signal, [math]\frac{y}{x}[/math] will be rounded to the nearest interval, instead of being recorded as it is. I was deducting it just now. But thanks for the answer.

Oh, analogue signals are the continuous signals. I couldn't think about them because i thougt they had a limit due to natural properties.

Oh, i got it now. The x in the middle of ZxZ indicates this binary operation is a cartesian product, right? So, this is a binary operation, are there other kinds of binary operations that are not cartesian product? Then, the monoid is something that suggest a operation inside a set, right?Could it suggest only binary operations or is it possible to suggest a n-ary operation? Thanks in advance.

I'm reading a book on DSP, and they say that there are discrete and continuous kinds of signals. I can imagine some discrete signals, but i have no idea of what could a continuous signal be. Can you suggest some?

I understand now what is a binary operation, now i have a problem with your statement: I've read a definition on wikipedia about cartesian product: And i have this questions: -This kind of mapping make sense to me (the playing cards), but why would I map the elements of the cartesian product SxS to S? -Are there other kinds of binary operation on sets? -Are sets the same thing of lists in programming? I guess so, their nature seems identical. -When he says: (M, *), what's the meaning of *? Thanks in advance.

I do understand the concept of set, but not the concept of binary operation.

I've searched on wikipedia and wolfram mathworld, and i have a definiton on a book right in front of me: After that there are some properties. But I still can't understand it. Can you help me? Thanks in advance.