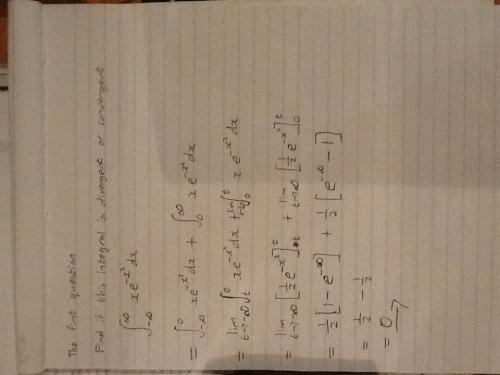Axioms

oh ok I see. Thanks =].

Av=Lv A(Av)=A(Lv) multiply both sides by A A(Av)=A(Av) substitute Lv = Av?? haha I'm still not getting that eurika moment. ----------------------------------------------------------------------------- This is what I tried but I am pretty sure it is wrong: Av=Lv (A-IL)v=0 (A-IL)(A+IL)=A^2 -IL+IL-L^2=0 A^2=L^2 ----------------------------------------------- I'm just not sure how to get the L^2 = A^2 answer with the way I understand your explination. I see the A^2 but dont know where you find the L^2. I guess I am just struggling with the principal idea of what they want.

I'm not sure where you are going with this. Sorry, can you explain a bit more?

Sorry for some reason the question never uploaded with the post: here it is: Let A be an nxn matrix with eigenvalue lambda(L) and associated eigenvector v. Use the definition (Av = Lv)to show that L^2 is an eigenvalue of A^2. Note: This is a special case of L^k is an eigenvalue A^k. Thanks for the reply =)

Attached is a question about a special case of eigenvector/values. I am not sure how to solve this and i cant find it in any of my text books or on the web. Any assistance will be greatly appreciated. This is what i have done. let L denote lambda Av=Lv thus Av - Lv = 0 (A-L)v=0 I try to square both sides here and I do eventually end up with the desired answer. But I have no idea if what I am doing is correct or not. Im just stabbing in the dark here.

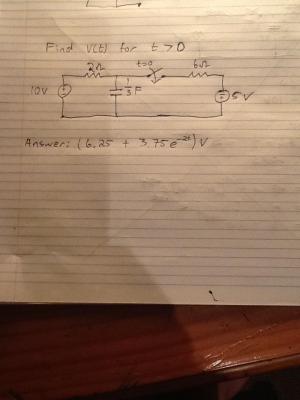
Ok I've solved it. Lol it was actually quite simple but I made it complicated >.<. My mistake when I tried node analysis initially was a sign error over the 5V source. That then took me to try to solve it with differential equations. I made the same sign error there =/. Well this is what I got. Anyone agree with me?

Hey. Ive been struggling to solve this circuit for a while now. They ask you to find v(t) for t > 0. They get 6.25V for the v(infinity). I have no idea how they get that value. Its a first order circuit so it shouldn't take anyone that long to solve. Ive tried every method that I know of to solve for v(infinity) = 6.25... I just dont get that value. By inspection I would have thought it would be 15V with Rth at 8Ohm. If you could just push me in the right direction, as in how to get the voltage across the capacitor at t = infinity, it would be much appreciated. The equation is: v(t)= v(infinity) + (v(0) - v(infinity))(exp(t/tau)) tau = RC v(infinity) = the steady state response v(0) is the transient response v(t) is the complete response Image of circuit is attached here:

I agree that the internal energy is constant. If I do the calculation I wanted you to do: Pressure(initial)*Volume(initial)= Pressure(final)* Volume(Final) therefore: Pressure(final)= [Pressure(initial)*Volume(initial)] / [Volume(Final)] therefore: Pressure(final)= (700kPa*0.1m^3) / (0.2m^3) = 350kPa Energy(initial) = 700kPa*0.1m^3 = 70kJ Energy(final) = 350kPa*0.2m^3 = 70kJ Thus there is no change in energy. Haha sorry I was wrong in thinking that there was a change in energy but I did not do the calculation until now. I also never realised that they placed it in a vaccume. Im used to questions where atmospheric pressure changes so I guess I just went on that basis. But still if you are not sure you can always just work it out. If it was for more than 1 mark then you would need a good explination, and showing the working will garantee your marks.

I am sure there will be a change in energy, acting on the walls of the system, because the volume increases and thus the pressure will decrease. If pressure decreases the energy of the atoms hitting the wall will be less because they have more space to move. Try isolating the first part of the system. You can then look at the second part of the system in isolation as well. Once you have done this you can compare and compute the change in energy. Maybe this is what your lecturer was looking for? There is a little trick with the units that you can do. I will give you the start and you can then try figure out what I mean. Remember Pa= N/m^2 J= Nm To compare pressure and energy using the data that was given: J = Nm = (N/m^2)*(m^3) = (Pa)*(V); [(isolated values!)] In words energy is equal to the pressure*volume of the system. That is what I would have done. A good tip to answering questions like that is to understand what each equation actually means. Try breaking your equations down into parts and see how they were derived. Once you have that understanding all the questions regarding the equation become simple because most of the questions require you to solve parts of the equations simultaneously. If you know what you need from each equation it will make life simpler in solving the problem. Edit: The internal systems energy will remain the same. But I am sure that is not what they were looking for because that is just theory. They would have also used the wording of internal system or something to indicate that they are looking for internal energy.

Thanks a lot for the help. I was stuck on this question for a while. I've never used erf in calculus before so I am not sure how you can identify it. Would it then be: erf(z)= 2/sqrt(pi)* integral(e^-y^2)dy from 0 to z? Not sure where you can get the erf values from though? I dont need to do it so its ok. I do this in other subjects though so it would be interesting to know how they combine it with pure culculus.

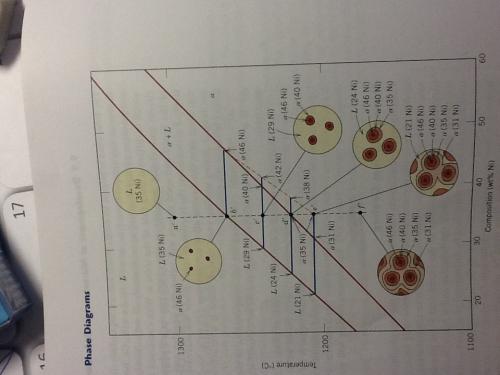
I don't understand what is going on in this graph. At the point e' there is a liquid phase outside the solidus line. The explination is that the diffusivity of the alpha phase is slower in non linear equilibrium phase diagrams. Point f'does not have the same liquid phase outside the solidus line. I guess my question is how do you determine when there will be no more liquid phase under the solidus line in a nonlinear phase diagram?

Any ideas? I still dont know how to integrate (e^-x^2). I assume you must integrate by parts. let u = (e^-x^2), du = (-2xe^-x^2), dv = dx, x = v. [integral of (e^-x^2)dx] = (e^-x^2)(x) - [integral of (-2xe^-x^2)(x)dx] ....1 let J = [integral of (-2xe^-x^2)(x)dx] Thus let s = x, ds = dx, dt =(-2xe^-x^2) t= (e^-x^2) Therefore J = x(e^-x^2) - [integral of (e^-x^2)dx] Substitute J into 1 [integral of (e^-x^2)dx] = (e^-x^2)(x) - [x(e^-x^2) - [integral of (e^-x^2)dx]] And this proves that zero = zero ........ -.- lol any1 know if this is the right track though? If I change s and t around and then sub from there maybe? I just cannot seem to simplify it. Probably missing something stupid or differentiation it wrong.

That is an interesting point. I always assumed that there would be a kind of "flow" of CO2 across the world due to changes in pressure. Has anyone ever taken readings of CO2 levels in the Sahara or places like that? I know in populated areas there are models but I cant seem to find anything on remote areas.

Their intentions are to use renewable energy sources to manufacture the fuel. They mentioned wind and tidal energy in the article. I think it is a new way to store renewable energy in a more efficient manner. What we normally think of with renewable energy is setting up a system that is going to supply energy to a nearby building or house etc. If you set up large refineries in remote locations ( The Sahara for example) you can now transport the energy, in the form of fuel, to areas that would need the extra bit of energy in the near future. There are just so many applications for this its ridiculous.

http://www.iol.co.za...89#.UIVBNaNvLc8 http://www.youtube.c...h?v=9jHRDFqk_Ys Air Fuel Synthesis in Stockton-on-Tees has produced five litres of petrol since August in this small refinery.

It took about 20min with rechecking.. I am sure anyone can solve this though if given enough time? It isnt that difficult, just tidius >.<

The moles would change. The OP doesnt say a solution of 250cm^3 of Na2CO3. If it is a solution then the moles will stay the same and then in iv) You could work out as the concentration in 250cm^3 = Xmol Na2CO3/ 1000cm^3. hmm I see in the first post you did say it is in water for the 250cm^3. Lol I just went on what you had said in the second set of questions. This is a good description.

Question 1 and 2 differ from the rest in my opinion. From question 3 Do they give you the density of Na2CO3? You can calculate how many moles it would be from mass = density * volume. You can then calculate how many mols are in that mixture. The concentration from this amount can then be calculated by taking the (calculated mols/ 750cm^3 H2O). This will give a unit of mols NaCO3/cm^3 H2O. If you need it per solution you can just manipulate the denominator. (calculated NaCO3 mols / 1000cm^3 sol). I dont know what units you want but I'll leave that to you. Concentration = kmol/m^3(sol) or kg/m^3(sol) in my experience unless you working with small values. The only relation I can see between the questions is if you have to calculate the density from what you had initially measured. i.e you take the amount you weighed and found what volume it occupies. This would be the bulk density and there are ways around it but then again I dont know if you got these values experimentally. This is how I would do it =/

The question doesnt make sense. If you have a certain mass it wont change unless you getting a mol percentage. Can you type the questions they give exactly then maybe I can help quickly. Im still waiting to see if anyone replies to my HW post >.<

No problem

Does anyone know where I can find worked out examples of comparison theory for indeterminate integrals? I cant find any good explinations in any of my text books. I need to remember how to tell if a graph is converging or diverging if the integral is indeterminate. What I know is that you compare it to a similar equation but i cannot remember what the conditions are in doing so. Any help would be appreciated >.<

Look at how you are expanding your brackets of (1+h)^2. It is the same as saying (1+h)(1+h)... From here you should get (1+ 2h + h^2) I dont know where you are making your mistake so if you could show what you did then that could be helpful. I am pretty certain though that you are not expanding your brackets and multiplying out correctly. Remember from (1 + h)(1 + h) you must multiply every term in the first bracket by every term in the second bracket: i.e. (1*1 + 1*h + h*1 + h*h). I think this was called FOIL.. First outter inner last or something like that. If you are still struggling look up bracket expansion and how to multiply out of brackets. (x+1)^3 = (x+1)(x+1)(x+1) = (x+1)(x^2+2x+1)= ((x^3)+(2x^2)+(x) + (x^2)+)(2x)+(1)) try expand this: (x+5)^2

I am struggling to remember the rules regarding e within integration. I know that the integral of e^x is e^x. This means that the integral of e^2x must be equal to (1/2)e^2x. (derivative of (1/2)e^2x = e^2x) Ok now I am having trouble with two integrals. I am getting the right answer for the one in the book but I am not sure if my method is right. Can anyone please confirm if my integration of (xe^-x^-2) is correct? (I get (1/2)(e)^(-x)^(-2) My next question is how do you integrate (e^-x^2). Do you have to manipulate it algebratically? I know you can determine if it is divergent or convergent with a comparison test. I basically just want to know how you would start the evaluation of the indefinite integral of (e^-x^-2)dx. Any help would be much appreciated.

Thanks, answer that was given was 49.3 lb/cuft though. Not sure what to make of it.