pengkuan
Senior Members-
Posts
196 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by pengkuan
-
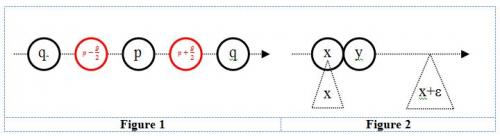
This is very sharp point. Thank you. I have corrected my definition of discreteness as below. Discreteness is the property that qualifies sets that are formed by isolated points. Isolation means these points are surrounded by points of other nature, like island is isolated by water. In the real line each rational number is surrounded by irrational numbers that isolate them from its rational neighbors. Let p and q be two rational numbers. The gap between them is g=q-p. We can create the irrational number p+g/pi that isolates p from q. When q®p, q never reaches p and the irrational quantity g/pi is never zero. Figure 1 shows the isolation of p from its neighbors q and q-. As p and q can be any rational numbers in the real line, the set of rational numbers is discrete over the entire real line.
-

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I agree that numbers with infinitely many digits have actually definite values, the limit of the sequences that you mentioned. This is commonly accepted. But in the discussion that I have about my article, I have found that there is some ambiguity that must be worked out. Essentially, as we cannot write infinitely many digits, a sequence does not equal its limit. So, I will discuss this point in detail later. I agree also that my point about the power set of natural numbers is confusing, because I have not given a definite one-to-one correspondence between the two sets. But I'm writing it now and I will inform you when it will be done. I was not aware that Russel's paradox was about power set in this way. It is a paradoxe when the set has finite members, but with infinite members, it is much less clear. -
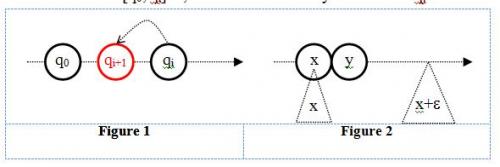
Sorry. I post below the detail of my point 1. Discreteness of set Discreteness is the property that qualifies sets that are formed by isolated points. Rational numbers are a discrete set whose elements are ratios of two natural numbers. For example q0 and qi , qi+1 is the mid point between the former. When i®¥, the number qi+1 approaches q0 without reaching it. Figure 1 shows the insertion of qi+1 between q0 and qi. So, however small the interval [q0, qi] is, there can be infinity of numbers qj for j > i such that q0 < qj < qi. As there are numbers between any two rational numbers, neighboring rational numbers are disjoint. This property defines the discreteness of a set. As q0 and qi can be any rational number in the real line, the set of rational numbers is discrete over the entire real line. 2. Continuity of set Contrary to the rational numbers, the set of real numbers is continuous, that is, any point on the real line is in contact with its adjacent points. “In contact” means there is no gap between these two points in which another number can be inserted. Figure 2shows 2 adjacent points x and y which are in contact and an interval [x, x+e], e being the width of the interval. Because the gap is zero, however small the width of the interval is, it can never be smaller than y-x. This property defines the continuity of a set. As x can be any point in the real line, the set of real numbers is entirely continuous. 3. Collectively exhaustive and mutually exclusive events When tossing a coin, all possible outcomes are heads or tails. The values heads or tails are said to be collectively exhaustive, that is, there is no other possibility. Also, when heads occurs, tails can't occur and vice versa. These two values are said to be mutually exclusive, that is, the outcome is either heads or tails, no mixed value is allowed, for example half heads and half tails. In a well ordered set, two neighboring points are either disjoint or in contact, there is no other possibility. So, disjoint or in contact are collectively exhaustive and mutually exclusive. Disjoint elements make discrete sets and elements that are in contact with one another make continuous set. Thus, discreteness and continuity are collectively exhaustive and mutually exclusive too and sets can only be discrete or continuous, no other possibility is allowed. 4. Continuum hypothesis The elements of any infinite discrete set can be put in an indexed list where each element uniquely corresponds to its index. This one-to-one correspondence between the elements and the natural numbers proves that the cardinality of any infinite discrete set is À0, for example the sets of the natural numbers and the rational numbers have cardinality À0. The cardinality of a continuous set is |ℝ|, like the real numbers. Because a set must be discrete or continuous, its cardinality must be À0 or |ℝ| and not strictly between À0 and |ℝ|. In consequence, the continuum hypothesis is true. 5. Cardinality of discontinuous subsets of real numbers Can discontinuous subset of real numbers have cardinality smaller than |ℝ|? The first possibility is to remove all algebraic numbers from the real line. The set of the real numbers depleted of all algebraic numbers is not continuous because the places of the algebraic numbers are holes. The cardinality of the algebraic numbers is À0. So, the cardinality of this subset is |ℝ|-À0. As we have |ℝ|-À0=|ℝ|, the cardinality of this subset is not smaller than |ℝ|. Second possibility is to remove real numbers proportionally, for example, removing 9 points in 10 from the unit interval [0, 1]. This way, it seems that the left points are only 1/10 of the original points. But removing 9 points in 10 is equivalent to removing 9 parts in 10 from the unit interval and the leftover numbers are equinumerous to 1/10 of the unit interval, that is, the interval [0, 0.1]. As the cardinality of [0, 0.1] is also |ℝ|, the cardinality of this subset is not smaller than |ℝ|. Another possibility is Cantor ternary set which is constructed in splitting an interval in 3 and removing the central one, then applying this process to the remaining intervals forever. This process seems to reduce the number of points indefinitely. But it turns out that the cardinality of this set is |ℝ|. Then we can remove all the irrational numbers from the unit interval [0, 1]. This way we are left with the rational numbers whose cardinality is À0. So, the cardinalities of the above subsets of the real numbers are either À0 or |ℝ| but not strictly in between. In consequence, construction of discontinuous subsets from the real line cannot give cardinality bigger than À0 and smaller than |ℝ| and the continuum hypothesis holds.
-
No, I have not these idea. Do these properties determine continuity or size of sets?
-
Here is my article Continuous set and continuum hypothesis.pdf
- 51 replies
-
-1
-
Your are right. Please see the section 5. Cardinality of discontinuous subsets of real numbers of my pdf in the original post. Thanks studiot Xerxes Thanks for intervening. My objective is to prove the continuum hypothesis. So, I distinguish discrete sets and continuum. By my definition of discrete set, all points are isolated. So they are disjoint. By my definition of continuum, all points are in contact with one another. Since points can only be disjoint or in contact, the points are in a collectively exhaustive and mutually exclusive game. So, discreteness and continuity are also collectively exhaustive and mutually exclusive. Because of the above property, sets are only discrete set or continuum. So, there can only be cardinalities of discrete set or of continuum, that is, À0 or |ℝ|. So, there cannot be cardinality strictly between À0 and |ℝ|. Hence, the continuum hypothesis is true. For my definition of discreteness and continuity. Also for discontinuous subset of real numbers. Please see here: http://pengkuanonmaths.blogspot.fr/2015/12/continuous-set-and-continuum-hypothesis.html
-
I have defined discreteness in section 1, surely not in formal language of mathematics. I cannot prove. The fundamental difference is continuity. I use this to prove that discrete set and continuous set have different cardinalities and there is not value in between. Size of the set is a result, not the condition. You are right. I haven't studied these matters. I learn in writing and discussing. Maybe. But I'm confident that there is something true in my claims. You have given a brilliant definition of the continuum of the real line that I'm not able to give. Thanks. And thanks for joining. You are not late. Intuitively the real line is a continuous line. So I have borrowed "continuity" to qualify the continuum.
-

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I have read the link of bijection.... I learned that domain is departure and codomain is arrival in some sense. -
I'm correcting the errors in it.
-

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Thanks. I must read carefully the link you have given. Since I'm not familiar with the formal language of set theory and I cannot understand things like "domain or codomain". Your help is useful in the future article I will write on the bijection between the natural number and its power set. Thanks for your advise. Effectively, bijection between binary numbers and the power set of the natural numbers is not the same thing than bijection between natural numbers and its power set. I will explain the latter bijection more carefully. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I will write a detailed proof of the bijection. But why the one-to-one correspondence does not prove the bijection? To any subset of the natural numbers, there is one and only one binary number like 0.154894................ with infinite zero behind or with infinite sensible digits. This is a bijection. Isn't it? My going back and forth is only due to the terminology I use to adapt with other people's objections. but the heart of my idea is the same. I have to write something on bijection. I said one-to-one is a bijection just to shorten one-to-one correspondence. -
This article explains why the cardinality of a set must be either Aleph0 or |ℝ|. In "Cardinality of the set of binary-expressed real numbers" I have shown that binary numbers cannot fill the unit real interval in spite of infinity of digits. In general, the members of a discrete set can only occupy isolated points in a continuous space leaving empty intervals behind. So, the fundamental difference between a continuum and a discrete set is the continuity, not the number of elements. Continuity and discreteness are collectively exhaustive and mutually exclusive. The cardinality of discrete set is aleph0, that of cintinuous set is |ℝ|. Because a set must be continuous or discrete, its cardinality must be either aleph0 or |ℝ|, but never in between. So, the continuum hypothesis is true. 1. Rational numbers are discrete 2. Real numbers are continuous 3. Collectively exhaustive and mutually exclusive events 4. Continuum hypothesis 5. Cardinality of discontinuous subsets of real numbers Here is the article in pdf Continuous set and continuum hypothesis.pdf Please read the article at PDF Continuous set and continuum hypothesis http://pengkuanonmaths.blogspot.com/2015/12/continuous-set-and-continuum-hypothesis.html or Word https://www.academia.edu/19589645/Continuous_set_and_continuum_hypothesis
-

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
In the beginning I wanted to explain that the binaries have length n=<1 that increases forever In another discussion, people remark me that my binary set is not of infinitely many digits. Indeed, they have finite digits that increases without end. So, they are in some sort always finite. So I have changed my terminology and say they have finite digits. But here you have another terminology. Hence the confusion. I think the term of infinitely many zero that flip with the subsets of natural numbers is a good compromise. This scheme makes a bijection between the binaries and the power set of naturals. For me the one-to-one is a bijection. So, my set of binaries has the same cardinality than the power set of the naturals. But this is in contradiction with the commonly accepted theory that states that the power set of the naturals is strictly bigger than the naturals and equals the reals. What I'm showing here is not the countable set of binaries has a bijection with the reals, but has a bijection with the power set of the naturals. In this case, the power set of the naturals has the cardinality of the naturals, not that of the reals. So, the theory that the power set of the naturals is strictly bigger than the naturals and equals the reals is false. Also, 2À0 is not the cardinality of the reals, but equals À0 -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
The subset of the even numbers is {2,4,6,8............}. This corresponds to the binary number with the even numberth digits flipped to 1. That is 0.010101010101010101................................. The length is infinite. Maybe you think that my set of binaries contains only finite length numbers. But it contains the infinite length numbers too. One-to-one is a bijection. The rationals are in a one-to-one with the naturals and is bijective. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
You are right. But if we append the finite binary numbers with infinitely many zero, we obtain a one-to-one correspondence with the power set of the natural numbers. Take 0.000000000....................... This binary number is zero plus point plus a infinite sequence of zero. Then we pair up each zero to one natural number that is the rank of place of the zero. We create a subset of the naturals and simultaneously flip the zero to 1 if the corresponding natural number is in the subset of natural number. This binary number corresponds to this subset uniquely. Then, we have a one-to-one correspondence between each binary number and one subset of the naturals. As the cardinality of the power set of the naturals is , the cardinality of the binary number so constructed is the same, . I know, thanks. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Sure! The discussions bring me back to the right way. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Length n is finite but goes to infinity. The cardinality of the power set of the naturals is computed this way. I'm not able to explain formally because I'm not a mathematician and lack the formal language of mathematics. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Ok. Non repeating no terminating digits give irrationals. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
The number of binary number is 2n, when n=infinity, n=À0 , so the cardinality of binary number is 2À0. As this is the cardinality of the power set of the naturals, this set must be the real. But the set of rationals does not contain irrational. So, the power set of the naturals is not the reals. I'm not proving. I explain. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Yes. Back to the origin. There are two sort of binary numbers, finitely many digits and infinitely many digits. The former are rational, the latter are irrational. In the section 1 of my article, I have shown that the cardinality of the former is 2À0 . This cardinality means they seemingly contains irrationals. But as they are rational, the cardinality 2À0 must be that of rational, which I showed afterward. Those with infinitely many digits are said to be irrational numbers. But I find that they do not have last digits, so we do not have their exact values. So, they cannot not be used as numbers. We use pi as point in the line, but not as 3.1415926.................. No operation is done using its infinitely many digits form. So I think binary numbers with infinitely many digits are not numbers at all because they cannot be used. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Irrational number does not have last digit. It was a typo. They do not have definite digital value. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Infinitely many digits number do not equal irrational number because without the last digit, it cannot have definite value. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
For me binary numbers are 0+.+sequence of n digits with n going to infinity. n is finite at any stage. In fact, a number with infinitely many digits does not have sense. When one says irrational have infinitely many digits one does not means it have actually infinitely many, but it does have a last one, which means that the binary number does not have a definite value. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Sorry. I do not understand your reasoning. What are "objection ", "rows " or "does not require you to 'count' every member"? What is my "contradicting proofs must be invalid"? What are you trying to prove? Binary numbers are countable? Uncountable? -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Because infinitely many digits have no sense. They cannot be used to perform mathematics. Yes, but this term does not emphasize infinity that is the crux of the problem.