pengkuan
Senior Members-
Posts
196 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by pengkuan
-

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Of cause "binary numbers" of finite length are a set of the same size than the natural numbers. When I said "in some sort "less countable" " it was to just to emphasize that binary numbers are countable, not as real numbers which are uncountable. What does this mean? This is to get the transfinite number aleph 0 directly for 2n=2À0 without saying "n goes to infinity and n=aleph 0" . Binary numbers are a subset of the rationals, so they have the cardinality of the natural numbers. What I'm saying is not that binarys have the cardinality of the reals 2À0 , but the power set of the naturals has not the cardinality of the reals, but that of the naturals. In fact, fractional binaries cannot write all the reals in [1,0[ because they cannot have infinitely many digits. They are only rationals. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I agree that I was wrong in saying that my path passes through 1/3. Actually, it does not, nor through 1/5, /7, 2/5 3/5 ...... So, it is clear that binary numbers are less numerous than rational numbers. So, binary numbers are in some sort "less countable" than rationals rather than uncountable. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Actually, it does not pass through 1/3, but it will at infinity, where 1/3 is 0.010101010101010101010101010101010101010101010101010101..... In fact, in order to pass through 1/3, we have to use 3 base numeral system. Why are infinitely many binary numbers countable? In fact, they don't. They cannot exist. You can never express the expansion of a irrational number completely. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Yes. They are not the same set. Many people cross off the same fractions in their zigzag counting. In fact, the fractions with all the ratios, even identical value, is equivalent to the 2D natural numbers, which is equinumerous to the natural numbers. rational is a subset of the 2D. So, is equinumerous to the natural numbers. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
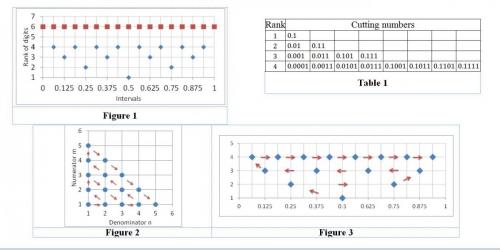
An infinitely long sequence of digits to the left has to be proven to exist before use. If a notion exist in mathematics, it have to be created properly. Creation of real numbers. https://en.wikipedia.org/wiki/Construction_of_the_real_numbers If real numbers are self evident, why did Cauchy invent his sequences and Dedekind his cuts? So, infinitely many sequence of binary digits must be created properly. Before this, infinitely many digits to the right is just an assumption, an assertion that has not been proven. Can root 2 be properly defined? Let root 2= s_n+s_oo, where s_n is the first n digits and s_oo the left infinite long string of digits. For computing the digits of root 2, we can do: (s_n+s_oo)^2=2 We have s_oo=root 2-s_nx Or solving the order 2 equation s_oo^2+2*s_nx*s_oo+s_nx^2-2=0 Solving this equation gives: s_oo=(-2*s_nx+root(2*s_nx*2*s_nx-4*s_nx+4)/2 We have the same result. So, for knowing the right infinite long string of digits, you have to know the right infinite long string of digits before you compute. Thus, you cannot know at all. If you cannot create root 2 from a known string of digits, you will not be able to get it anyway, even in theory. BTW, How to write symbole here? In the beginning g of my article, I counted the number of elements of binary numbers till aleph_null just to show what is the state of knowledge now. Then in the other sections, I show that in fact, binary numbers can be counted using intervals cutting. This technique only count finite binary numbers, but it goes to infinity of digits. This counting do not reach aleph_null. Because binary numbers do not included infinitely long sequence of digits, my counting is complete. Here are the figures The counting does pass through 1/3 for every finite digits and goes forever. But actual infinitely many digits to the right cannot exist, as I explain in the post above. If the infinity of digits does not exist, finite binary numbers going to infinity of digits completely list all binary numbers. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Yes. this what Cantor have proven. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I have shown this in 4 ways. 1 By cutting the interval [0, 1]. You can cut this interval in 2, then the second rank interval in 2, then the third in 2.................. The intervals are never fill with binary number. This is shown in figure 1 2 By connecting the cutting points with arrows and make a path like the zigzag for rational. This path goes in a single line forever passing through all binary numbers. This is a one-to-one correspondence with the natural numbers. Figure 3 3 By counting the number of n digits binary numbers. There are 2^n of them. When we let n go to infinity, there are a countable number of them. 4 By noting that all finite binary numbers are rational. Then when n, the number of digits go to infinity, the binary numbers stay rational. So, the set of binary numbers is a subset of rationals and they are countable. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Yes. When n→∞, it has to start from 1, then +1 then +1 ...... At each step, n is a finite number. This is THE problem. How can n become aleph_0 without first has been a finite number? One cannot leap to aleph_0, one just go the old way, 1+1, then +1, then +1 . During the process, the intervals are all empty. At the end, since there is no end, the intervals will never be filled. There will be empty intervals between numbers, binary or decimal or in any base. In fact, n is not kept finite, but cannot be infinite, that is, never n=aleph_0. So, real number cannot be mirrored by digital numbers. As never n=aleph_0, even in theory, the set of real numbers cannot be created from natural numbers using power set. This why Cantor's diagonal argument is not true. For me, binary number is 0.101011110011..................... and there is no end to the digits. A real number can be expressed in base 2 this way. When I count the binary number, I count those having finite digits and infinitely many digits. So, the set that I count is normally the set of real numbers. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Your are right. Real numbers are uncountable. I have tried to prove that binary numbers are countable. By the same reasoning, decimal numbers are countable. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
I present that "binary numbers has the same cardinality as the real numbers" as the present situation of knowledge, this is not my point. In the following, I showed that the set of binary numbers, including infinite digits numbers, has the cardinality 2^aleph0. This is also the present knowledge. But in the "2. Fractional binary numbers on the real line" and "3. Countability of BF", I showed that this is not the case, that the set of binary numbers, including infinite digits numbers, has the cardinality aleph0. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
This is true. one real number has more than one binary expansion, one binary expansion have only one real number. But this does not change the cardinality. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
Thanks. Here is the paragraph "The binary expansion of a real number is a sequence of 0 and 1 with a point. On the right of the point is the fractional part and on the left the integer part. As every real number has at least one binary expansion, the set of all binary numbers must have the same cardinality than the real numbers. In fact, we can actually count the elements of this set which will be denoted by B." What is the flaw that you see? It's ok for me. -

Cardinality of the set of binary-expressed real numbers
pengkuan replied to pengkuan's topic in Mathematics
What is "paragraph 2"? "Counting the fractional binary numbers" or "Fractional binary numbers on the real line"? -
Cardinality of the set of binary-expressed real numbers This article gives the cardinal number of the set of all binary numbers by counting its elements, analyses the consequences of the found value and discusses Cantor's diagonal argument, power set and the continuum hypothesis. 1. Counting the fractional binary numbers 2. Fractional binary numbers on the real line 3. Countability of BF 4. Set of all binary numbers, B 5. On Cantor's diagonal argument 6. On Cantor's theorem 7. On infinite digital expansion of irrational number 8. On the continuum hypothesis You can read the article in the pdf below or the link below Cardinality of the set of binary-expressed real numbers.pdf Cardinality of the set of binary-expressed real numbers PDF http://pengkuanonmaths.blogspot.com/2015/12/cardinality-of-set-of-binary-expressed.html or Word https://www.academia.edu/19403597/Cardinality_of_the_set_of_binary-expressed_real_numbers
-
Sorry. I'm trying to integrate a pdf but I cannot find how. I had posted photos years before, but I do not remember how either. This is a proof for Fermat's Last theorem: By transforming the equation x^n+y^n=z^n, I arrived to the conclusion that z must be irrational. Taylor's series and continued fraction are used to prove this. The complete proof is here: http://pengkuanonmaths.blogspot.com/2015/07/on-fermats-last-theorem.html
-
On Fermat’s last theorem This theorem states that for any n except 2, the equation X^n+Y^n=Z^n is not true for any positive integer triplet X, Y and Z. Fermat’s “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.” has fascinated mathematicians from 1637 but no one has found what his proof was. Let us try to understand this theorem better. Please read the article at On Fermat’s last theorem http://pengkuanonmaths.blogspot.com/2015/07/on-fermats-last-theorem.html or On Fermat’s last theorem https://www.academia.edu/13665056/On_Fermat_s_last_theorem
-
I have published a new article. From now on, I will publish my articles in in my Science Forums' blog. Please read here http://blogs.science...s.net/pengkuan/
-
Deformation of EM wave signals 14 August 2012 Electromagnetic wave carries signals emitted by antenna into space. The EM field of a wave is mathematically defined by the EM wave equation whose monochromatic solution is the equation (1). A signal is a time varying EM field that can be expressed by Fourier series which is the sum of monochromatic wave functions, that is, a sum of equation (1) of different amplitudes and wave lengths. We notice that the amplitude and phase of the equation (1) vary with distance and frequency, that is, monochromatic EM waves of different frequencies evolve differently in space. In consequence, the form of the Fourier series is distorted, the traveling signal is deformed. What is the extent of the deformation of EM signal in space? Please read the following document Deformation of EM wave signals http://pengkuanem.bl...ve-signals.html
-
Displacement magnetism experiment design 31 July 2012 According to Ampere-Maxwell equation, displacement current creates magnetic field. I call this theory displacement magnetism. I have proven that displacement magnetism violates energy conservation law and as a consequence, the wave equation is inconsistent (1,2,3). The above conclusions need experimental test. I propose an experiment whose design is shown in the Figure 1. A round plate capacitor is charged by an alternate current, Ic. In the circuit a long rectangular loop is connected in series. The magnetic field variation in the space between the plates and outside the capacitor is measure by an EMF sensor. Another EMF sensor measures the magnetic field near the long side of the loop. Please read the following document Displacement magnetism experiment design http://pengkuanem.blogspot.com/2012/07/displacement-magnetism-experiment-design.html
-
Thank you for your kind indication. I will keep it for future. I was explaining you the effect that seemed to puzzle you, not arguing about it. For semiconductor, I'm sure that holes do not feel Lorentz force. I can explain you the mechanism if you want.
-
Hello studiot. Your are not treating semiconductors, but conductors. There is not hole at all. The effect you observe is probably due to magnetic susceptibility . Silver is a diamagnetic material, that is, it creates a magnetic field contrary to external one. But Aluminium is paramagnetic, it creates a magnetic field paralelle to external one. The susceptibility of silver is −2.6 10e-5, that of Aluminium is 2.2 10e-5. It is a small value, but inside the material, the distance between electrons and magnetic sources is nearly 0. The Lorentz force can be significant. Since sliver creates a negative magnetic field, its Hall effect is positive. Aluminium creates a positive magnetic field, its Hall effect is negative. The difference of volatge intensity is due to conductivity. Sliver is a much better conductor than Aluminium , its voltage is stronger. pengkuan
-
If I understand the problem, the question is: while the charge carriers are electrons in N type semiconductor, the stream of electrons are deflected upward in presence of magnetic field; why the holes in P type semiconductor are also deflected upward? Logically, holes are positive charges and must go downward. I think that in P type semiconductor, the current is also a stream of electrons, because only electrons can move, holes are fixed charges in crystals. When the electrons flow, the hole they left are where they were before moving. As streams of electrons are deflected upward, the holes they leave are where the electrons move, that is, on the up side. So, the holes seem to be deflected upward too. In fact, it is not the holes that are pushed up, but the moving electrons. On the down side, electrons are not moving and all holes are filled.
-
I am sorry. I did not well understood your post. I have not noticed that it was about semiconductor specifically and that the deflection of positive charges was the crux. Now, if I have understood the problem, the deflection of streams of negative charge is correct, but that of positive charges is contrary to Lorentz force law. Is it right? The positive charge carriers are holes, isn't it? They do not move, but it is the departure of electrons that leaves the hole.
-
Electromagnetic Wave Paradox 23 July 2012 In 2 previous articles, I have shown that the magnetic field generated by displacement current violated energy conservation law. But, this type of magnetic field was involved neither in Lorentz force nor in EMF. Its only use is for electromagnetic wave. Here, we will check the consistency of electromagnetic wave equation. Please read the following document Electromagnetic Wave Paradox http://pengkuanem.bl...ve-paradox.html
-
Phantom Lorentz force Paradox 16 July 2012 I have exposed an inconsistency of Ampere-Maxwell equation, in the article "Displacement Current Paradox" http://pengkuanem.bl...nt-paradox.html This equation states that displacement current creates magnetic field and EMF. However, "Displacement Current Paradox" shows that this EMF would violate the energy conservation law. Magnetic field has 2 properties, EMF and Lorentz force. Let us study the Lorentz force created by magnetic field associated to displacement current. The Figure 1 shows a round plate capacitor charged by an alternate current Ic, and a wire loop in which circulates a constant Il. The varying charge of the capacitor creates a displacement current and then a magnetic field, which in turn, exerts a Lorentz force on the current loop. Please read the following document Phantom Lorentz force Paradox http://pengkuanem.bl...ce-paradox.html