pengkuan

First, thank you for speaking so kindly and giving valuable information. It's a pleasure. For the magnetic shield, I do not need the shield to screen completely the field, a diminution is enough. Suppose that without the shield, the internal force of the triangle is zero. With the s3 in the shield, the magnetic field on the s1 and s1 will diminish and so does the force on the ensemble s1+s2. As the force F3 does not change, the total internal force will have a resultant toward the left. More complex is when the length of the shield varies, and the field on s1+s2 will increase or diminish. What will compensate this variation of force? No law exists to describe this case. By the way, why s1 and s2 will be attracted to the shield if the field from s3 will be inside the shield? For the Biot-Savart law, no explicit text forbids the use of it for part of a circuit.

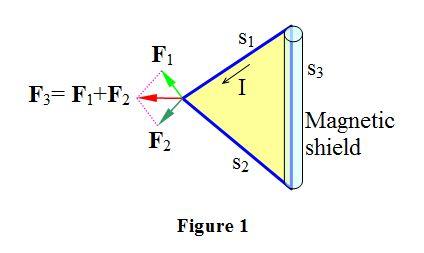
Paradoxical Lorentz force internal to a triangle coil Take a rigid triangle coil (Fixed on a wooden plate, yellow in the Figure 1), a current I flows in it. The 3 sides would feel a Lorentz force from the magnetic field of the other sides. These force are internal to the coil. Now, put the side s3 inside a ideal magnetic shield. So, the sides s1 and s2 would not feel the magnetic field from the side s3 and the latter does not feel that from s1 and s2. What will be the total internal force on the triangle in this case? The side s3 would feel no force. The side s1 would feel the Lorentz force F1 from the side s2 and the side s2 the Lorentz force F2 from s1 respectively. So, the total internal force of the triangle coil is F3= F1+F2. As the forces F1 and F2 are Lorentz forces, they are perpendicular to their sides and they make an angle between them. Their resultant force F3 is non null. If the total internal force is non null, any movement in the direction of the resultant force would do a work and create a energy. This is impossible because energy cannot be created. So, the fact that the Lorentz force is perpendicular to the current violates the third Newton's law and the energy conservation law. This is the paradox of the internal Lorentz force.

thanks

Please read what you said: your objective is to win. Look at how you speak in previous posts. So , let it be. You win. But you did not solve the paradox, because you are thinking in term of voltage source plus resistor. Only in this way, the current can vary with an additional tension. I have said all the way that the current is imposed by the current source. You did not listen to me at all and insisted on using voltage source. So you do not analyse the same circuit than me. It does not solve my circuit's paradox for sure.

you win but the paradox stays

In my physics , we use 2 types of ideal electric source, voltage source and current source . voltage source: tension U0 does not change. deliver 1 A, 2A 100A ... with the same tension. current source: current I0 constant. deliver 1V, 2V 100V .... with the same current. You use a "current source", that deliver I, say 1A, then, with tension 1V (due to emf), the current becomes 1+0.1A, if the tension is 10V (emf), the current is 1+10*0.1=2A This is a current varying source. It is of unknown kind. you are talking about another circuit than me. The mine does not conserve energy. The your, I don't know.

We do not have the same physics. For me, the current is I, imposed, the voltage between its 2 electrodes is U. The power is I U. During time dt, the energy is I U dt. In the loop, the curent is I, the voltage is EMF. So, the energy is dW(emf)=I.U(emf) dt.

The current source does work dW(emf) = I U(emf) dt= I l B dx, The Lorentz force does work dW(mec) = F(Lorentz) dx= I l B dx They are equal. I l B dx=I l B dx, dW(emf) = dW(mec) see above

I have done an error in the last image. Please use this one instead.

yes

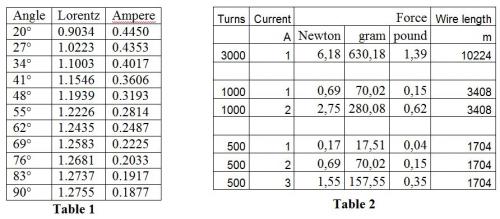
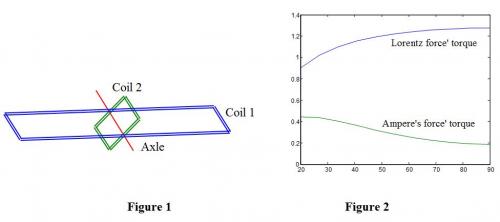
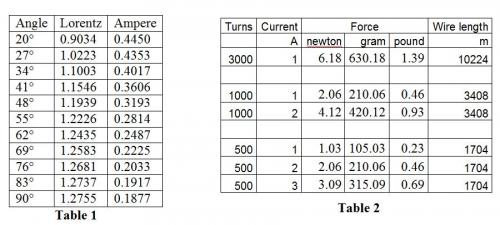
Links removed. Does someone agree that the paradoxes are well-founded? If you agree, are you interested in doing an experiment to check the validity of these paradoxes? In case of success, the first person who does it would deserve a scientific prize. Below is the design of the experiment. Check experimentally the paradoxes about Lorentz law Although the paradoxes show the deficiency of the Lorentz force law and the differential Ampere's force law (an improvement of the Lorentz force law) has successfully solved all these paradoxes, it is however necessary to confirm this by new experiments never carried out before. The suggested experiment makes 2 rectangular coils interact. The coil 1 is horizontal, the coil 2 is tilted at an angle with respect to the coil 1 (See the Figure 1). The magnetic force will create a torque on the 2 coils, which are calculated numerically. The parameters are the following: The dimensions of the horizontal coil: lx=0.4 m, ly=0.8 m The dimensions of the tilted coil: lx=0.36 m, ly=0.144 m The current in the 2 coils: I=3000 A•turn The results predicted by the Lorentz force law and the differential Ampere's force law are the 2 curves drawn in the Figure 2. The torque varies with respect to the angle between the 2 coils. The values of the torques are given in the Table 1 in N•m. We see that, as the angle increases from 20° to 90°, the torque predicted by the Lorentz force law increases whereas the prediction of the differential Ampere's force law decreases. The values of these torques are very different; for example, at 90°, the Lorentz force law predicts 1.2755 N•m, against 0.1877 N•m for the differential Ampere's force law. The values and the shape of the curves are sufficiently different to distinguish if the measured values is in accordance with the differential Ampere's force law or the Lorentz force law. The difference of the torques is due to the magnetic force between perpendicular segments of currents. The Lorentz force between perpendicular segment of currents is non null, whereas for the differential Ampere's force law, this force does not exist. This is why when the angle between the 2 coils is 90°, the torque for the Lorentz force law is strong and the torque for the differential Ampere's force law is nearly 0. The quantity of wire is calculated here. The lengths of each turn of the 2 coils are: l1=(0.4+0.8)*2=2.4 m l2=(0.36+0.144)*2=1.008 m There are 3 000 turns in each coil. The lengths of wire of the 2 coils are: L1 = 7 200 m L2 = 3 024 m The total length of wire needed is : 10 224 m We will measure the force on the top of the coil 2. At angle 20°, the expected force is: F0 = 0.4450 N•m / 0.072 m = 6.18 N We can use different values of current, size of coils. The expected forces at angle 20° are calculated and are given with the corresponding currents, wire lengths in the Table 2. To prove experimentally the inconsistency of the Lorentz force law is of the greatest importance for physics. The reader is encouraged to carry out this experiment and try to be the first to accomplish this great task.

The work of external force is in my post this: dW(mec) = F dx= I l B dx (I have done a typo, it is dW(mec) here, not dW(emf)) yes

compensated by the current source. yes. The change is in the calculation of motors.

The current is imposed by the current source. That is, the loop that passes through it has the same current what ever it happens. So, in the bar the current is I and is independent of v, even there is an emf. This is the point.

You mean in the same loop, the current in the current source is different from that in the bar? Yes, you really think "The current from the EMF is not the same as the current from the current source; ". They are in series.

I have said with a link Wikipedia In circuit theory, an ideal current source is a circuit element where the current through it is independent of the voltage across it. You know it is a current source but you still make your current vary. It is wrong Yes there is external electric work, dW(emf) = I U dt= I l B dx, in my post.

I have only I, not i. If you consider another current i, which is different, you are not talking about my circuit.

what is i? and I?

u=0

It is a loop. The current is the same all over the loop.

The property of a current source is to keep the current constant. Wikipedia In circuit theory, an ideal current source is a circuit element where the current through it is independent of the voltage across it.

It is an ideal case, current is constant, independent of v. Joule heating is not cnsidered.

The force that keeps the bar moving at v does work W1, the emf of the bar does electric work W2 they cancel. W1-W2=0

ok I gather the 3 paradoxes in one thread so that when I give this one address to people they could read all. It is in the mechanical work.

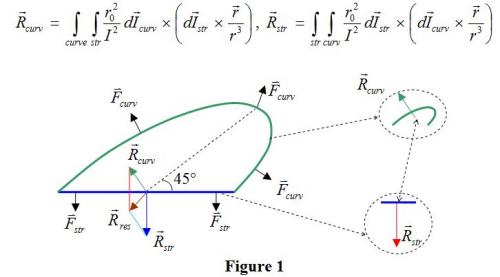
Internal Lorentz force paradox A current in a magnetic field feels theLorentz force. For isolated coil, the Lorentz force on a current segment is dueto the magnetic field of the coil itself, that is, the Lorentz force isinternal to the coil. Let us study the coil shown in the Figure 1, which is rigid and is composed of a curved part and a straight part. The Lorentz force that the straight part acts on the curved part is Fcurv, that the curved part acts on the straight partis Fstr. Fcurv and Fstr are integrated to give the total Lorentz forces on the curved part, Rcurv and on the straight part, Rstrrespectively. Rcurv and Rstr are mutual Lorentz forces and, respecting the third Newton's law, their sum should be 0: Rcurv +Rstr =0 But, does the Lorentz force law really predict 0 for this sum? The 2 total forces are calculated numerically. The calculated force are dimensionless. The length of the straight part is 2, the height of the curved part is 1 and the inclination 45°. The numeric values of the dimensionless forces are as follow: The forceon the curved part Rcurv : Rx=-6.4618, Ry =9.5457 The forceon the straight part Rstr: Rx=0 Ry=-16.8930 The equations that give these values are: The total forces Rcurvand Rstr are drawn in the Figure 1 and are not parallel. But why? In fact, the Lorentz force on the curved part is always perpendicular to the curved wire, and itsintegral has a x component. The Lorentz force on the straight part is vertical and has only y component, that is: Rcurv = Cx*i + Cy*j, Rstr= 0*i + Sy*j Now we add them up to find the resultant internal force: Rres =Rcurv +Rstr= Cx*i + (Cy + Sy ) *j ≠0 Rres is the sum of all internal forces of the coil. As it has a non null x component, Cx, its y component is (Cy+Sy)and is non null for our numerical calculation, Rres violates the third Newton's law. If real internal force had non null value, one could make the following process: Make a coil with inclined curve and straight wires, put the current on, and then let the coil move in the direction of the resultant force Rres. Since the magnetic flux passing through the coil is constant, the current will not do any work. But Rres would do a work in the movement, creating a quantity of energy. This is impossible because energy cannot be created. Rres is predicted by the Lorentz force law, so, the Lorentz force law does not correctly predict internal magnetic force. I call this inconsistency the "Internal Lorentz force paradox". yes, it was included.