pengkuan

Thank you for the remark. I forgot to precise that there is an external force on the bar, which is equal to the Lorentz force.

I'm sorry, I do not see.

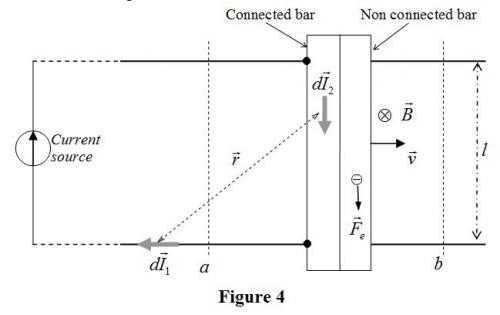
Lorentz' EMF paradox The "B-cutting paradox" concerns the energy balance. Let us see the creation of electromotive force by the moving bar. The conductor bar's free electrons feel a vertical Lorentz force in moving horizontally, which is denoted . But, is there really an electric tension? The force is constant for steady velocity and constitutes an electrostatic field, . Obeying electrostatic laws the free electrons flow and distribute them-self to induce an electrostatic field so that the resultant electrostatic force on all free electrons inside the conductor bar is 0 and the surface becomes an equipotential. So the 2 points of contact with the 2 horizontal wires have the same potential and the tension is 0. In order to understand this phenomenon, we imagine an identical conductor bar jointed on the one connected to the 2 horizontal wires. But this bar is insulated from the conducting bar and the horizontal wires. The 2 bars are called connected bar and non connected bar (See the Figure 4). Evidently, the electric field in the non connected Bar is 0 and the surface is an equipotential. The connected bar is in exactly the same electromagnetic situation but caries the current of the coil. According to the superposition principle, the electric field is not influenced by the current. Thus, the surface of the connected bar is also an equipotential and the tension between the 2 contact points is 0. Another point of view is that the potential is proportional to the energy that a free electron acquires in movement. Along any path inside the connected bar the line integral of the resultant electrostatic force is 0. Thus, the free electrons of the current get no energy at all. Again, the tension is 0. This conclusion puts the Lorentz force law in opposition with the electrostatic law. I call this opposition the "Lorentz' EMF paradox".

I know perfectly that any current, even electron beams, form loop. Have I said I do not? In this discussion and by this paradox, my objective is to show that Lorentz law is inconsistent somewhere, even it is valid for most of our use. You said So, you recognize that it fails for the situation of the shielded parallelepiped. If I said before the discussion that Lorentz law is inconsistent, would you agree? Now, you know even where it fails, and for a situation pretty common. But is it an unphysical situation? One can perfectly make this experiment physically, isn't it? Does it break other physical laws?

Did you say Lorentz law fail? At least for some cases? Do you use Lorentz law to calculate the deflection of an electron beam? If Lorentz law fail for current that does not closes in loop, it should not be used for electron beam, nor in accelerators. The vacuum TV set would not function neither.

This is the very paradox I point out. I established that mutual Lorentz forces for non-parallel wire segments do not cancel using Lorentz law. I established also that they cancel using Newton 3. So, this is the Lorentz law's inconsistency.

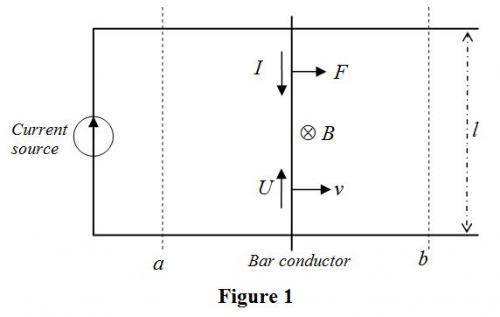
B-cutting paradox about emf generation An electromotive force can be generated either by a variation of magnetic flux or by a moving conductor cutting the magnetic force lines (B-cutting). For example, in the set-up shown in the Figure 1 the bar conductor with length l moves at the velocity v cutting the force lines of the magnetic field B. The generated electromotive force is: U = B l v A current source provides a current I which will do an electrical work against U. For constant I, when the bar moves from the position a to the position b, the quantity of work is: dW(emf) = I U dt= I l B dx On the other hand, the current-carrying bar will experience a Lorentz force: F=I B l Let us calculate the mechanical work the Lorentz force does to the exterior when the bar travels the same distance: dW(emf) = F dx= I l B dx We see that the mechanical work is equal to the electrical work: dW(emf) =dW(mec) So, no extra energy is left in the coil. However, the energy conservation law is not respected. Indeed, the magnetic energy stored in the coil depends on the positions of the bar. For positions a and b, the energies are respectively: Ea =½ La I² and Eb=½ Lb I² As the self-inductance Lb is greater than La, the magnetic energy stored in the coil is greater for position b than a: Lb >La =>Eb> Ea This implies that the coil has gained an extra quantity of energy: Eb -Ea>0 But from where? If this were true, we could make the following machine. Imagine the above coil in a space free of magnetic field. The machine functions in the following way: 1) The bar is at the position a, I=0, Ea=0. 2) The current increases to I, the current source does the electrical work. 3) The magnetic energy stored in the coil is Ea =½ La I² 4) The bar slides in the magnetic field created by the other 3 sides. The bar goes to the position b, the current source does the electric work W(emf), the Lorentz force does the mechanical work W(mec). W(emf) and W(mec) cancel out and the coil has not gained any energy. 5) But, the stored magnetic energy is now. Eb=½ Lb I² 6) The current decreases to 0, the coil gives back the stored magnetic energy to the current source. In this cycle, the current source has gained the energy Eb-Ea. 7) The bar goes back to the position a with no current, thus no work. 8) Restart from the step 2). After n cycles, the quantity of energy the current source would get is n( Eb-Ea ). This is impossible because energy cannot be created. Thus, the principle of this process is incorrect. I call this inconsistency the "B-cutting paradox".

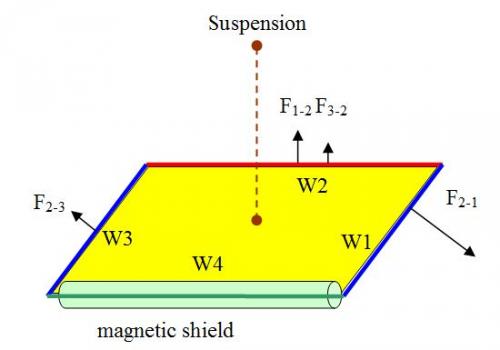
I am not ignoring the other force, please read my previous post. But if you say Would you mean that I should not assume R123=0 if I take R4-123 into account? That is, if I add the force R4-123 on W1+W2+W3, the resultant force R123 would change its value? This reasoning is like saying that: The force between 2 electrons is (C*qq/r²). But if I put a proton near them, the force (C*qq/r²) will change. Why? Is the distance r changed? Or the charge of electrons? Or the coefficient C? You said: Right. But there is a physical way to prevent that the wire W4 exerts a force on W1+W2+W3. Look at the figure. I put the wire W4 in a magnetic shield; Thus, the magnetic field of W4 does not influence W1+W2+W3, neither W1+W2+W3 influence W4. The shield does not carry current. Then I hang the coil plus wooden plate through a string. In this case, the resultant force on the coil is only R123 which is non null. Will the coil move or turn? If yes, there is creation of energy. If not, R123 is 0. That is, the value of R123 predicted by Lorentz force law is wrong. You said in a previous post: You mean, R123 can have a non null value for you. Do you still think so?

In physics, there are quantities that are invariant. The Lorentz force is invariant. That is, it does not depend on reference frame. The Newton 3 law is also invariant, that is, it gives the same result what ever the coordinate system. If you charge the W1+W2+W3 with electric charge, the resultant force is 0, what ever the coordinate system you use. If there is current in W1+W2+W3, the Newton 3 applies too and R123 must be 0. Why do you say can you give an argument?

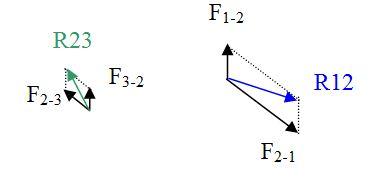
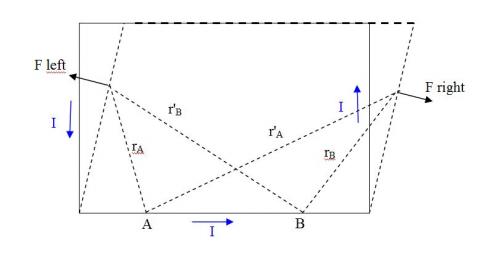
Sorry. F2-1//F2-3 means they are parallel and can be added together. So (the component x of F2-1 + F2-3 ) >0 F1-2 and F3-2 are vertical. They do not have x component. I understand that you do not have enough time to reflect carefully, and you have mixed mutual Lorentz forces and direct action-reaction forces. You said F1-2+F2-1 = 0 and F3-2+F2-3 = 0 This is true if they were direct action-reaction forces. But F1-2 and F2-1 are mutual Lorentz forces and are at an angle (please use right hand rule to find the direction of Lorentz force) so F1-2+F2-1 = R12≠0 and F3-2+F2-3 = R23≠0 And they do not cancel out.

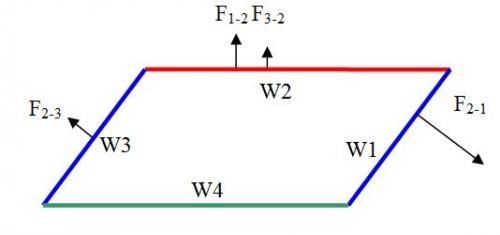
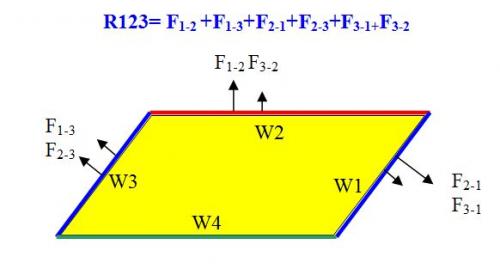
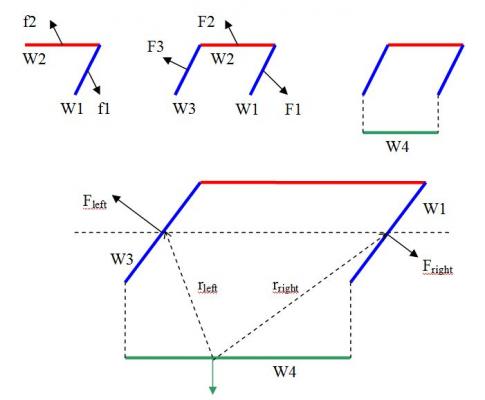
I have to say sorry because this math is wrong. Let us take the resultant force on the W1+W2+W3: Rres=F2-1+F3-1+F4-1+F1-2 +F3-2 F4-2+F1-3+F2-3+F4-3 We divide Rres into two groups: Rres=(F1-2 +F1-3+F2-1+F2-3+F3-1+F3-2 )+(F4-1+F4-2+F4-3) We denote: R123= F1-2 +F1-3+F2-1+F2-3+F3-1+F3-2 R4-123= F4-1+F4-2+F4-3 R4-123 is the force from W4 to W1+W2+W3. R123 is the sum of the forces from W1 to W1+W2+W3 from W2 to W1+W2+W3 from W3 to W1+W2+W3. That is, R123 is internal to the ensemble 3 rods W1+W2+W3 bounded to the wooden plate (yellow parallelepiped). So, Newton 3 requires R123=0. But, with the above consideration, Symmetrically, F3-1 cancels F1-3. we have: R123= F1-2 +F3-2+ F2-1+F2-3 As the average distance between W2-W1 is shorter than that between W3-W2, We have F2-1//F2-3 and the x component (F2-1+F2-3)x>0. So, the resultant force R123 is non null: R123≠0. The force R123 internal to W1+W2+W3 violates Newton 3. So, if we had Rres=-R4 in the previous math, it was because R123 violated Newton 3. We have tried to save the Lorentz force law which violated Newton 3 for a 4 sides parallelepiped by using a internal force that violated Newton 3 for 3 sides. It is not good physics.

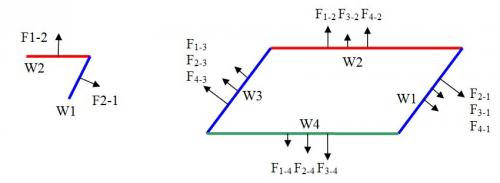
If you affirm only the minus sign exists, I suppose it is not an affirmation based on approximate feeling and you have done the math properly. If not, here is my proper math. See the figure. F1-2 is the Lorentz force on the rod W2 due to the magnetic field from W1. F2-1 is the Lorentz force on the rod W1 due to the magnetic field from W2. Globally, there are 3 Lorentz forces on each rod. The resultant force on the W4 is: R4=F1-4 +F2-4+ F3-4 The resultant force on the W1+W2+W3 is: Rres=F2-1+F3-1+F4-1+F1-2 +F3-2 F4-2+F1-3+F2-3+F4-3 Physically, the couple W1-W2 is the same as W3-W4, and W1-W4 is the same as W3-W2. So, F2-1=-F4-3 and F4-1=-F2-3, so they cancel out. Symmetrically, F3-1 cancels F1-3. So, Rres=F1-2 +F3-2 +F4-2 By symmetry, we have: F1-4 =- F3-2 , F2-4=- F4-2, F3-4=- F1-2 So, Rres=-( F1-4 +F2-4+ F3-4) In conclusion, we have: Rres=-R4 Is-it this math right? Version 3 of the article https://docs.google.com/open?id=0B5-G5ctz2vmbUl8tNGQ2Nk9UQlM2eG80UlIzVFlXZw

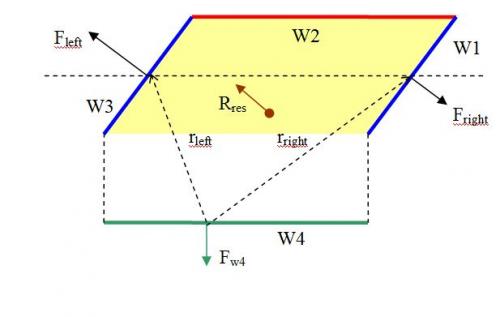
Well, you can critic me for not saying everything. I have using a rigid coil. That is, the W1, W2 and W3 are connected rigidly so that all force W1 receives are transferred to W2 and W3. But, to make this idea obvious, I bound W1, W2 and W3 on a wooden plate, the yellow surface in the figure. This way, we can sum all forces that the wires receive and their resultant force R res is on a point within the plate. R res does not balance with F w4, breaking Newton 3.

Ok. Let us take the problem only physically. No math at all. Take 2 rods, W1 and W2. Their mutual force are f1 and f2. f1+f2=0 because Newton 3 and the rods do not move. Now add a third rod, W3, on which the force from 1 and 2 is F3. The Force on the other rods have changed. Let denote the mutual forces on each rod as F1,F2,F3, and their sum Fr=F1+F2+F3. Because Newton 3 and the rods do not move, Fr=0. This must be true for any kind of force, electrostatic, gravitation, magnetic….. Question: If F1, F2 and F3 were Lorentz force, do we have Fr =F1+F2+F3=0 or Fr ≠0? What is your answer? We must suppose Fr =0. If not, Newton 3 is violated already. Now close the coil with rod 4. The connections (dashed lines) are soft and do not transmit force. Even with current on, the internal force (Lorentz force) within the ensemble 3 rods W1+W2+W3 must be 0, that is Fr=0. So, we can study the Lorentz force that the rode W4 exerts on W1+W2+W3 without drawing F1, F2, F3 Fr. The Lorentz force is originated from the Biot-Savart law, that is, it is inversely proportional to the distance between the interacted currents. We know that the average distance between W4-W3 (r left) is shorter than that of W4-W1 (r right). So, the resultant Lorentz force F left is greater than F right. Thus, F left- F right>0 The resultant Lorentz force from W4 on the ensemble W1+W2+W3 has a x component to the left, denoted Fx. The Lorentz force on the W4 is vertical, thus the x component on the ensemble W1+W2+W3+W4 is Fx. This is not allowed by Newton 3. Version 2 https://docs.google....0bGlOMVVLRVhIZw My Email adress:titang78@gmail.fr

I respect your point of view. But if you do not point out what is the error, I cannot explain why.

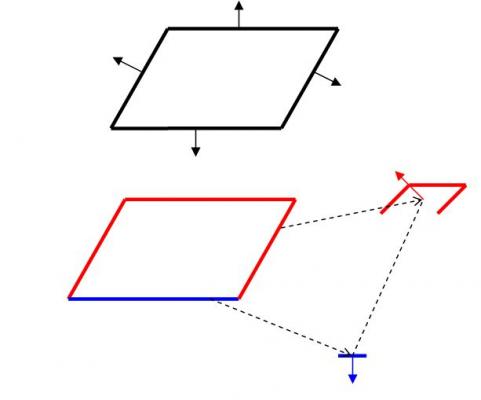
Seeing your drawing, I have understood what is the "trouble" you are talking about. You are considering the resultant force on each side from all the other sides. That is, in the figure here, the back arrows, and their sum is 0. This is not my view. I am considering the lateral sides plus the top side as a whole part, the red part, and the bottom side another part, the bleu part. The tree upper sides feel a resultant force from the bottom, the red arrow, and the bottom from the 3 upper sides, the bleu arrow. The bleu and red arrows do not cancel out. The Newton's law is a law, no matter how you cut your coil, the resultant forces must cancel out. However, when you cut it into red and bleu parts, the resultant force remains non null. This is the problem of the Lorentz force law. The raison I have used curved and straight coil is that you cut intuitively the coil into curved and straight parts and this leads to trouble. Our discussion is good in that it makes clear the cutting of the coil.

Because the sides and the forces F right and F left are parallel . I can sum them and find Fx. I have used a triangle in my previous numerical calculation. It was not better.

Here is a mathematical proof that the x force is not 0. See the drawing and the pdf. parallelepipede.pdf The full article with the parallelepiped proof integrated.internal.pdf

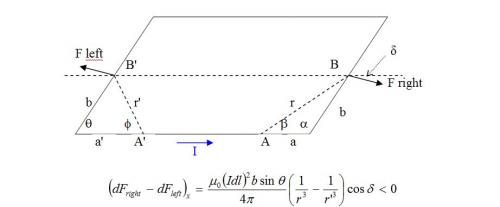
Thank you for your comment. It makes me to think for those who do not do numerical calculation about the resultant force immediately; i.e almost everyone. Here is a simple graphical explanation. I will do a mathematical demonstration if necessary. Take a rectangle coil. The Lorentz forces from the point A on a segment of the vertical sides are F left and F right. When the rectangle is sheared an angle to the right, the distance rA will shorten and r'A lengthen, and F left will increase and F right decrease. For the symmetric point B, there is the same variation of the forces. The x components will vary in the same sense approximately. So, there will be a resultant force on the upper sides with a x component.

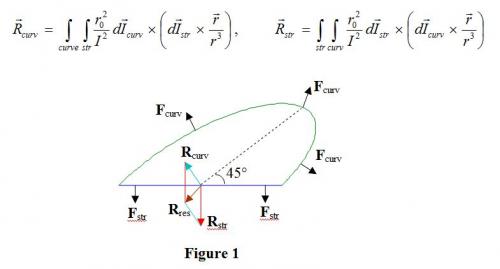
Internal Lorentz force paradox A current in a magnetic field feels the Lorentz force. For isolated coil, the Lorentz force on a current segment is due to the magnetic field of the coil itself. This force is internal to the coil and its resultant is 0. Let us see the internal force of the coil shown in the Figure 1. This coil is composed of a curved wire part and a straight wire part. According to the Lorentz force law, the magnetic force is always perpendicular to the current, as indicated by the forces Fcurv and Fstr in the Figure 1. The resultant force on the curved part is Rcurv and that on the straight part is Rstr. Rcurv and Rstr are forces internal to the coil, thus their sum must be 0. But, is the sum predicted by the Lorentz force law 0? I have done a calculation for this coil in dimensionless form. The length of the straight part is 2, the height of the curved part is 1 and the inclination 45°. The numeric values of dimensionless forces are as follow: The resultant force on the curved part: Rx= -6.4618, Ry =9.5457 The resultant force on the straight part: Rx= 0 Ry =-16.8930 The resultant force on the curved and straight parts are calculated as follow: These forces are drawn in the Figure 1. As we see, Rcurv and Rstr are not parallel and give rise to a resultant force Rres. If the real internal force conforms to this prediction, one could make the following process: Make a coil with inclined curve and straight wires, put the current on, and then let the coil move in the direction of the resultant force Rres. This force would do a work in the movement. Since the magnetic flux passing through the coil is constant, the current will not do any work. Thus a quantity of energy is created by Rres. This is impossible because energy cannot be created, hence an inconsistency. Why the result forces on the 2 parts of the coil are not parallel? Because Lorentz force is always perpendicular to current. On the straight part, the Lorentz force is vertical. But on the curved part, the Lorentz forces on every segment are inclined due to the direction of the current. So, their resultant cannot be vertical. In fact, because of the direction of the segments of currents, for any coil of non symmetric shape, the resultant Lorentz force internal to the coil cannot be 0. Thus, the Lorentz force law does not predict correct internal magnetic force. I call this inconsistency the "Internal Lorentz force paradox". For reading the solution and more information, please read this link or the pdf document. My link Aharonov_net.pdf