JMessenger

Had someone ask by email something, so thought I would put the explanation here also. Take the scalar potential definition of Wikipedia http://en.wikipedia.org/wiki/Scalar_potential The potential P is assumed to be a function of the coordinate system, for example P(x,y,z). For a 3 dimensional scalar field there is a scalar value assigned to each coordinate point. If a directional derivative (gradient) is take [math]\frac{\partial P(x,y,z)}{\partial x}+\frac{\partial P(x,y,z)}{\partial y}+\frac{\partial P(x,y,z)}{\partial z}[/math] we obtain F. This definition of F however is technically incomplete. The question must be asked on whether or not P(x,y,z) is integrable. The reason is that the definition I just described of a scalar field is based on a understanding of the same type of plot as [math]\Phi[/math] above. There are always two scalar values assigned to each point for an integrable function. In the case of [math]\Phi[/math] there is [math]|\Phi|[/math] and the magnitude of a constant [math]|C|[/math] which is assigned a magnitude of 0 in this particular case. A more general case is that of the flipped integral, where the two assigned scalar values are [math]|\Phi^{alt}|[/math] and the magnitude of a constant with a non-zero value. While the directional derivatives are identical, the two scalar values must be retained for each point in order for the integrals to stay the same. Stated another way, the scalar field as shown on Wikipedia is actually composed of a minimum of two scalar fields in order to be integrable. We normally think of one of those scalar fields as a zero scalar field and being unimportant, but this is not the most general case.

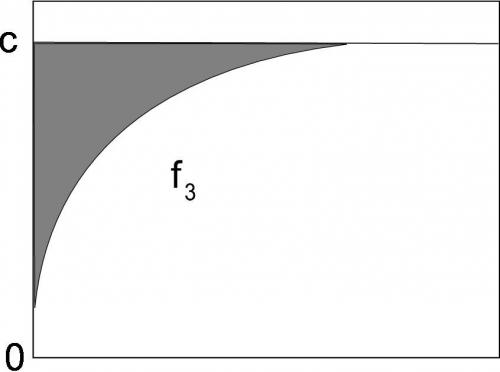
Let's stick with the explaining [math]\Phi_{alt}[/math]. Changing notation to [math]\Phi^{alt}[/math] A more technical explanation of the Poisson equation can be found here:http://eprints.ma.man.ac.uk/894/02/0-19-852868-X.pdf In this case u is equivalent [math]\Phi[/math]. [math]\Phi[/math] is shown in and as a function of a single cartesian dimension [math]x_0[/math] (listed as r with boundary conditions for [math]\Phi\rightarrow\infty[/math] as [math]r\rightarrow 0[/math] and [math]\Phi\rightarrow 0[/math] as [math]r\rightarrow\infty[/math]) and [math]\Phi^{alt}=f_3[/math] as an arbitrary translation along the vertical axis and is defined such that [math]\frac{\partial \Phi}{\partial x_0}=\frac{\partial(C-\Phi_{alt})}{\partial x_0}=\frac{-\partial\Phi_{alt}}{\partial x_0}[/math] and that [math]|\Phi(x_0)|=|C-\Phi^{alt}(x_0)|[/math] (boundary conditions for [math]\Phi^{alt}\rightarrow -\infty[/math] as [math]r\rightarrow 0[/math] and [math]\Phi^{alt}\rightarrow C[/math] as [math]r\rightarrow\infty[/math]) The first point being made (that doesn't seem related yet) is that one cannot tell the magnitude of the function within the Poisson in relation to a constant of integration (the first derivative of each function is identical). Nor can one speak definitively of whether a vector equated to a directional derivative points away or towards a load function. It is subjective based on whether or not a constant of integration is present. In other words, you can't technically state that a "field" is attractive (nor repulsive) if the field is based on the Poisson equation. The point I will be making is that the Poisson is only an approximation for a more accurate model of field theory, but I will argue that one of these identical functions should present a better approximation to another model.

It does seem pointless at the beginning but I would maintain that this is due to our mental understanding of directional derivatives of static scalar fields. Looking at the below picture, it cannot be determined from the directional derivative which integral was the source function: since for instance we can get or equivalently, if modeling the constant scalar field as orthogonal vectors with a sum of zero, (ignore the notation). The symbols don't make sense since I would have to define a physical model that would be the counterpart to the stress-energy tensor in this model. That isn't immediately necessary to make a definition akin to [math]G_{\mu\nu}=\kappa T_{\mu\nu}[/math] just yet as the first question at hand is whether or not a constant of integration of a scalar field becomes a scalar multiple of the metric. If the Poisson equation doesn't differentiate between [math]\nabla^2\Phi[/math] or [math]\nabla^2(C-\Phi_{alt})[/math] and if there is no known way to solve the magnitude of the cosmological constant with respect to the magnitude of the Newtonian phi, I would first ask on what a priori basis do we choose one scalar form over the other?

Back again after discovering the wonderful text The Genesis of General Relativity. Nordstroem's theory of gravity was the last scalar field theory of gravity that was a challenge to GR. Once the bending of light was verified it was mainly forgotten except as a teaching tool for General Relativity. What is fascinating about it is that the scalar fields have a tensor equivalent of [math]R=\kappa T[/math]. According to http://www.pitt.edu/~jdnorton/papers/einstein-nordstroem-HGR3.pdf the regular Newtonian scalar function [math]\Phi[/math] was used originally within a Laplacian and then with the D'Alembertian as it was a simple logical choice (Einstein had also attempted the first Nordstroem theory previously). What neither of them may have considered is determining whether or not [math]\Phi[/math] is an integrable function (and can provide an integral for gravitational energy). Assuming that it is, for a static three dimensional "field", even if the integral is "flipped" it does not change any subsequent derivatives. Meaning [math]\frac{\partial\Phi}{\partial x_u}=\frac{\partial(C-\Phi_{alt})}{\partial x_u}[/math]. Note that unimodular gravity considers the cosmological constant also as a constant of integration, but when Einstein introduced a physical use for the cosmological constant, he did so using the Poisson equation but didn't include it within the differential operator (2nd equation of Cosmological Considerations on the General Theory of Relativity). In the tensor equivalence though for the alternate scalar field, it would seem that we should arrive at something like [math]\eta R g_{\mu\nu}-R_{\mu\nu}=\Gamma g_{\mu\nu}-T^{alt}_{\mu\nu}[/math] (instead of [math]R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=G_{\mu\nu}-\Lambda g_{\mu\nu}=T_{\mu\nu}-\Lambda g_{\mu\nu}[/math] which doesn't meld with QFT). I am attempting to see if using this field equation I can take the difference of [math]\Gamma g_{\mu\nu}-\kappa T_{\mu\nu}[/math] as a change in the vacuum expectation value of QFT where this is equivalent to baryonic energy density. In simple terms I am using a region of baryonic energy density as a decrease in vacuum energy density, or equivalently inverting the energy scale of baryonic energy relative to the classical zero energy of the vacuum. This would also seem to be able to mesh with Noether's theroems using the flux of a decrease in density rather than the flux of a positive or negative density. Anybody want to help derive the field equations? Probably not going to be easy.

From the looks of it, anything about f(x) or tangents is extraneous. You were actually only asked to find an equation of a line that is parallel to another line. By changing nothing more than the y intercept on the given line equation, you found "the equation of the...line..parallel to the line...". It sounds like a trick question designed to test your reading comprehension, which you got correct. You could have substituted any number in place of 1/4.

There is the known analogue between a Ricci flat manifold [math]R=0[/math] and the Laplacian [math]\nabla^2\Phi=0[/math] (both source free). My basic desire is to show a link between Einstein manifold [math]R=4\Lambda[/math] or [math]4\Lambda-R=0[/math] and a Laplacian of the form [math]\nabla^2(C-f)=0[/math] (would also be source free). It does also get into densities within stress-energy tensors later, which is even more interesting to me, but this would need to be proven first. Ok the real motive is that the geometers who write under the name Arthur Besse are offering a free meal to whom ever comes up with a solution heh. It would help bolster my case if I can find other known differential topology problems that this would solve. I have read somewhere that there is a Minkowski space problem, but can't find the specifics of what was meant by that.

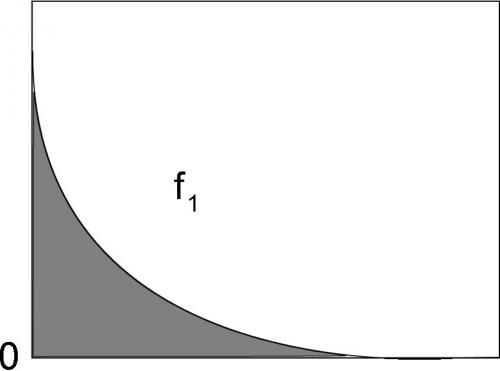
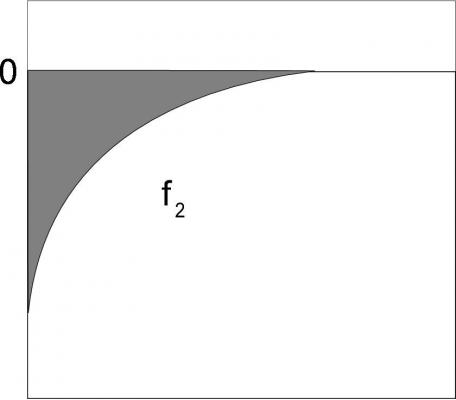
Hi all, I am researching a hypothesis and looking for anyone who is familiar with differential topology (specifically Einstein manifolds). I have access to the Besse book Einstein Manifolds but am also looking for any open questions in differential topology that I am not aware of. I am attempting to develop a solid proof link between the Laplacian and Einstein manifolds (listed in the book as not found yet). The math is pretty basic, sort of a gauge theory of the Laplacian. In graphical form (as the equations might be confusing without them) there is no distinction between the derivatives of the following plots: therefore for a higher dimension scalar field there won't be any distinction between gradients nor the divergences of the functions: [math]\nabla^2f_1=\nabla^2(0-f_2)=\nabla^2(C-f_3)[/math]. If [math]\nabla^2(C-f_3)=0[/math] are components of a four dimensional scalar field and are normalized I should get a flat signature of [math]diag[1-1,1-1,1-1,1-1)[/math]. If the field has Lorentzian invariance then by setting the constant of integration portion to zero we get [math]diag[-1,1,1,1)[/math]. This would be the same as the link between Ricci manifold and EInstein manifold.

In GR, a Ricci flat manifold is a special case of an Einstein manifold with a "vanishing" cosmological constant. Here, [math]G_{\mu\nu}[/math] is theorized to have "vanished" since it was defined as the stress-energy tensor of matter. [math]R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=\Lambda g_{\mu\nu}[/math] Einstein manifold (arbitrary multiple of the metric remaining, no accepted physical theory, when viewed this way is measured to have a very small value) [math]R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=\Lambda g_{\mu\nu}=0[/math] Ricci flat manifold (zero curvature)(classical GR, but doesn't fit with current observations due to appearance of positive accelerating expansion) In this theory, the equation is viewed mathematically the same but physically different: [math]\frac{1}{2}R g_{\mu\nu}-R_{\mu\nu}=\Omega g_{\mu\nu}-L_{\mu\nu}=0[/math] This is viewed from the mathematical context that [math]\Omega g_{\mu\nu}[/math] is a Rank 0 tensor ([math]g_{\mu\nu}=[-1,1,1,1][/math], meaning [math]\Omega g_{\mu\nu}-L_{\mu\nu}=0[/math] (curvature vanishes) holds true for any arbitrary value of [math]\Omega[/math], including zero. In this theory, the only vacuum solution would be that [math]\Omega g_{\mu\nu}-L_{\mu\nu}=0[/math] with [math]\Omega\neq 0[/math] and perhaps based on Planck length. The major difference is that in GR, [math]G_{\mu\nu}[/math] is restricted to being a Rank 2 tensor, and must "vanish" for flat spacetime, whereas [math]L_{\mu\nu}[/math] is not restricted to being a Rank 2 tensor and can become a Rank 0 tensor for flat spacetime. In the special case when [math]\Omega g_{\mu\nu}=0[/math], THEN [math]L_{\mu\nu}[/math] would reduce to classical GR and thus be required to "vanish" (instead of becoming a Rank 0 tensor).

An interesting aspect of looking at it this way, is that for a perfect fluid stress-energy tensor, when the density at a point decreases (from flat), the pressure would appear to increase in order to follow [-1,1,1,1] and [1,-1,-1,-1]. [math]\Omega g_{\mu\nu}-L_{\mu\nu}=\left(\begin{array}{cccc} \Omega-L_{00} & 0 & 0 & 0 \\ 0 & L_{11}-\Omega & 0 & 0 \\ 0 & 0 & L_{22}-\Omega & 0 \\ 0 & 0 & 0 & L_{33}-\Omega \end{array}\right)[/math] [math]T_{\mu\nu}=\left(\begin{array}{cccc} C_{\rho}-\kappa\rho^{res}_{00} & 0 & 0 & 0 \\ 0 & \kappa p^{res}_{11}-C_p & 0 & 0 \\ 0 & 0 & \kappa p^{res}_{22}-C_p & 0 \\ 0 & 0 & 0 & \kappa p^{res}_{33}-C_p \end{array}\right)[/math]

Heh, I was wondering if you were actually reading these posts. The [math]L_{\mu \nu}\equiv G_{\mu \nu}[/math] is incorrect, but it will also take some time for me to fully understand [math]\Omega g_{\mu\nu}-L_{\mu\nu}=G_{\mu\nu}[/math]. If they truly are equal, for any value of the metric, then why would they predict anything differently? That is the reason I was curious to see your version of including the CC with the derivation of Newtonian gravity. I can come up with a specific radius for when gravity switches over to repulsive but I need to make sure I understand the assumptions in each step. I don't just want rote memorization, I would like to understand the logic that goes behind each. Takes time and learning as I go.

It gives me one extra option for flatness. In GR when [math]\rho[/math] vanishes, so does [math]G_{\mu\nu}[/math] and the curvature. In what I am proposing, when [math]\rho_{res}[/math] matches the background [math]C_{\rho}[/math], then the difference between them vanishes along with the curvature. Neither [math]L_{\mu\nu}[/math] vanishes nor [math]\Omega g_{\mu\nu}[/math]. I do not think this relationship holds true for non-flatness, but with [math]\Omega g_{\mu\nu}-L_{\mu\nu}=G_{\mu\nu}[/math], if I set [math]\Omega g_{\mu\nu}=0[/math] then L is nothing more than the negative of the Einstein tensor.

I am not sure I understand how they are the same. Take for example the [math]\kappa T_{00}[/math] for slow velocities as described by GR. As [math]\rho[/math] increases [math]\uparrow[/math], the stress energy increases and gravity increases. Taking my example [math]\kappa T_{00}[/math] of a perfect fluid, [math]\Omega g_{\mu\nu}[/math] would represent the density [math]C_{\rho}[/math] in a neighborhood about a point. [math]\L_{\mu\nu}[/math] would represent the density of a the fluid at a point [math]\rho_{res}[/math]. If the point density is equal to the surrounding density, there is no stress-energy [math]C_{\rho}-\rho_{res}=0[/math], but the more the density [math]\rho_{res}[/math] decreases [math]\downarrow[/math] with respect to the surrounding [math]C_{\rho}[/math], the higher the stress-energy [math](C_{\rho})\leftrightarrow-(\rho_{res})\downarrow=\uparrow[/math]. In the description by GR, the "energy density" [math]\rho[/math] increases from zero (with respect to what, the vacuum?), whereas I am proposing that the density decreases with respect to its neighborhood. I see how these might produce similar answers, but I don't see how they are equivalent. I will have to take some time to review the other things you posted. I do appreciate it.

I have read this before but I don't understand how this helps move us forward as a physical model on how to determine the structure of vacuum energy or how it relates to the standard model of particle physics. The [math]\rho[/math] of matter and energy is dynamical ( I can have particles with different masses and energy that dynamically change the stress-energy value at a point) and hence it is associated with terms that have indices ([math]\mu\nu[/math] of [math]G_{\mu\nu}\equiv \kappa T_{\mu\nu}[/math]). The [math]\rho_\Lambda[/math] is associated with a constant term that has no indices ([math]\Lambda[/math] and thus does not have the ability to vary in these indices. It does have the metric [math]g_{\mu\nu}[/math] associated with it and I am still working on understanding precisely what this means. I have seen it explained that the metric is a property of spacetime. There are a couple of things I would like to understand from your point of view and perhaps you can also expound on them from the point of view of Lagrangian mechanics. The Ricci tensor [math]R_{\mu\nu}[/math] appears to me to be a dynamic term (hence the [math]\mu\nu[/math] indices), whereas the Ricci scalar [math]R[/math] appears to be a non-dynamical potential term. Would this be true? Can you give the derivation of exactly when [math]\Lambda[/math] shows up in the derivation of [math]G_{\mu\nu}[/math]? It perhaps is in MTW, but as the text is almost 40 years old it would be nice to see a fresh take on this. My motivation is whether I can formulate a complete theory of gravity based on multiplying both sides of [math]R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=G_{\mu\nu}-\Lambda g_{\mu\nu}[/math] by -1 and changing (in order to differentiate the differences) [math]G_{\mu\nu}\equiv L_{\mu\nu}[/math] and [math]\Lambda g_{\mu\nu}=\Omega g_{\mu\nu}[/math]. So for my definition of flat spacetime (no matter or energy) I would get [math]\frac{1}{2}R g_{\mu\nu}-R_{\mu\nu}=\Omega g_{\mu\nu}-L_{\mu\nu}=0[/math] with [math]L_{\mu\nu}=\Omega g_{\mu\nu}[/math] and [math]g_{\mu\nu}=diag[-1,1,1,1][/math].

I think we are starting to talk past each other, although I have found some of your comments very useful. I am approaching tensors from a very basic level, and with GR being so well developed there is a gap that I would have to close in order to be able to effectively communicate each and every difference. One of my points is that even the equation [math]R=4\Lambda[/math] doesn't inform me precisely of the mathematical purpose of [math]\Lambda[/math], nor its value. The only explanations of it I have found are some conjectures that it may be related to QFT and that it appears to oppose gravity. As far as I can tell, most of the predictions from these don't lead to anything we physically observe. After all this time and effort by some of the brightest mathematicians, that just seems strange for such a simple term. I was familiar with simpler forms of tensors before I started this, and it occurred to me that with higher rank tensors you could lose information if you weren't careful. I was curious how classical GR handled this and as far as I can tell, it doesn't. I could rewrite the stress-energy tensor of a perfect fluid again to illustrate my point, but this doesn't seem to have helped previously in our discussion.

That is a bummer. There is nothing magical here, and I do agree that it is simple.Taking the derivative of a function may be equivalent to taking the derivative of a function plus a constant, but the same is not true in reverse. The anti-derivative does not give you the function. You could argue it via Occam's Razor, but that is just lazy and not rigorous. You cannot take the derivative of the following functions and determine which was the original function [math]f'_1[/math] or [math](C-f_2)'[/math] If the other images didn't help explain it, then not sure that one will help either, though. Agreed. Perhaps I can use this and relate it to what I was stating in the linked paper. I will combine what you stated above and the formula they give and see what happens here. Let's take equation 1.2 [math]\alpha \mu + \beta\frac{\partial \mu}{\partial n}=g[/math] This was supposed to be for a normalized vector on a surface so we will change this to [math]\alpha \mu + \beta\frac{\partial \mu}{\partial x_i}=g[/math] Combining the notation you gave, for example [math]f(x^u)=\alpha\mu_1=k_1^*[/math] and [math]a^v(x^u)=\beta\left(\frac{\partial \mu}{\partial x_1},\frac{\partial \mu}{\partial x_2},\frac{\partial \mu}{\partial x_3}\right)=(k_1,k_2,k_3)[/math] The problem with what you wrote is that the scalar [math]k_1^*[/math] is most certainly not the same type of scalar as [math]k_1[/math]. The first is a true scalar (like the absolute temperature at a point) and the other is the magnitude of a vector (such as the rate of change of a temperature in a basis direction).