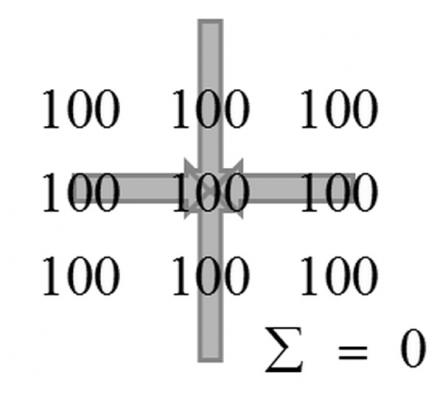JMessenger

Just as a comment, Faraday theorized that light waves have a pair of co-traveling wavefronts (to account for bi-refringence) but I don't think it necessarily follows that these wavefronts could be separated and "intersect at a distance".

True, but as you are a mathematician and forgetting all physical models, doesn't it bother you that a constant scalar (with the metric) appears in a geometric theory but there are no foundational proofs of its purpose?

Interesting find. They have a normal stress energy tensor for matter and also one for the Gravitational Aether. Seems to complicate the theory (and provide no path for answering dark energy) but I like their boldness.

Heh, I imagine that route has quite a bit of "mathematical fertility" but might not be the most direct route for some of my questions, so I will bow out of asking further along those lines (can I take a raincheck?). I am interested in how the metric is related to the cosmological constant, so it revolves around the physical understanding and derivation of a constant scalar with various metric values (including unimodular where the determinant magnitude of the metric is 1). What is your view of the relationship between the metric and the cosmological constant?

You had mentioned earlier about the theory having an additional scalar field, seemingly non-dynamical. I do need to look at the action of the theory later on and develop that, but going to expound on the stress energy tensor of a perfect fluid for a moment: In this tensor [math] T^{\mu\nu}_{normal}=(\rho+p)\mu^{\mu} \mu^{\nu}-p\eta^{\mu\nu} [/math] there are two scalar values of [math]\rho[/math] and p, which are scalar values of density and pressure. The problem I have with this tensor is that it was borrowed from hydrodynamical theory based on Newtonian concepts. What isn't stated is that the scalar values have an implied "+ 0" with them, as in "[math]\rho + 0[/math]" and "p + 0". What is just as valid with these scalars is to measure density and pressure from a higher magnitude, as in "[math]C_{\rho}-\rho[/math]" and "Cp-p" so that we get [math] T^{\mu\nu}_{alternate}=(C_{\rho}-\rho+C_p-p)\mu^{\mu} \mu^{\nu}-(C_p-p)\eta^{\mu\nu} [/math]. Although the constant scalars in this tensor (the "C") may not change value, they are not independent of the metric (same as the Cosmological Constant), so the alternate tensor should predict different answers (although that may only occur at large radii). The alternate stress energy tensor seems to instead describe a constant reduction in the density of a medium, that perhaps travels as a wave. Note that for [math]C_{\rho}-\rho=0[/math] (and the same for pressure), there is no stress in the medium and that for [math]\Lambda g_{\mu\nu}-G_{\mu\nu}=0[/math] there is no curvature. Edit: As an aside, I am aware of how the normal tensor is derived into 4-momentum and the "energy density" we are familiar with. I do have some questions concerning the definition of "flux" as it concerns "energy density".

Ha! I had to read that a couple times Hmmmm... Then the same should apply for R0, R1 and R2, no? Is there a rule concerning no-where vanishing tensors remaining in non-flat manifolds of R4 and higher? As in R0 remaining in R4, R1 remaining in flat R5, etc...as in Rn-4 for [math]n\geq 4[/math]?

Interesting, had not run across the phrase "not no-where vanishing". I can understand the part of having a manifold that is flat "in pieces", and that a no-where vanishing tensor that is non-zero at all points on a manifold, but can a manifold be completely flat, at all points and pieces, with a no-where vanishing tensor at all points and pieces?

But can a point in a region of zero curvature still have a non-vanishing tensor? ajb, You got me thinking about how textbooks on GR define certain things, and thumbing through a copy of The Large Scale Structure of Space-Time by Hawking and Ellis, and I ran across their definition of a vector: Technically, one could argue that this definition is incomplete, as we could equally write [math]\left(\frac{\partial f}{\partial t}\right)_{\lambda}|_{t}=\lim_{s \to 0} \frac{1}{s} \{f(\lambda(t+s))-K-f(\lambda(t))+K\} [/math] or [math]\left(\frac{\partial f}{\partial t}\right)_{\lambda}|_{t}=\lim_{s \to 0} \frac{1}{s} \{K-f(\lambda(t+s))-(K-f(\lambda(t)))\} [/math] where K is some arbitrary constant. In other words, their definition of a vector excludes the equally valid definition of a vector as shown in the below graph:

This may seem like rambling, but practicing how to relate this to those not familiar with tensors and for benefit of the forum to bring up failures in my logic. Taking into consideration the redefinition of the Einstein tensor that Misner, Thorne and Wheeler spoke about of [math]"G_{\alpha\beta}"=G_{\alpha\beta}+\Lambda g_{\mu\nu}[/math], and that there is no mathematical definition of "vanish", which is what I technically view as required (but lacking) for the equation [math]R_{\mu\nu}+\frac{1}{2}R g_{\mu\nu}=0[/math], I propose breaking it down to the most simple of mathematical arguments: Tensors in GR are represented through the use of 4x4 arrays or matrices. In order to sum two matrices, each component is summed with the corresponding component of another matrix. I propose the true definition for "vanishing" of the sum of two matrices is that ALL components must be exactly zero. For the special case of a matrix that can be written as [math]\left(\begin{array}{cccc} X & 0 & 0 & 0 \\ 0 & X & 0 & 0 \\ 0 & 0 & X & 0 \\ 0 & 0 & 0 & X\end{array}\right)[/math] we can sum this with a similar matrix of [math]\left(\begin{array}{cccc} Y & 0 & 0 & 0 \\ 0 & Y & 0 & 0 \\ 0 & 0 & Y & 0 \\ 0 & 0 & 0 & Y\end{array}\right)[/math] by individually adding each component to the corresponding component such that [math]X_{11}+Y_{11}=(X+Y)_{11}[/math] etc.. meaning [math]\left(\begin{array}{cccc} X+Y & 0 & 0 & 0 \\ 0 & X+Y & 0 & 0 \\ 0 & 0 & X+Y & 0 \\ 0 & 0 & 0 & X+Y\end{array}\right)[/math]. These matrices can also be written [math]X\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right)[/math] such that the sum is [math](X+Y)\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right)[/math]. For the sum of these two matrices to "vanish" absolutely, then [math]X=0,Y=0[/math] or [math]Y=-X[/math]. For the sum of two matrices (tensors) to allow [math]R_{\mu\nu}+\frac{1}{2}R g_{\mu\nu}[/math] to vanish exactly, then the form of the two tensors must be either [math]X=0,Y=0[/math] or [math](X-Y)\left(\begin{array}{cccc} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right)[/math].

On the subject of minimally coupled scalar fields, take the Wikipedia example: http://en.wikipedia.org/wiki/Scalar_field_solution under Einstein tensor [math]G^{\alpha\beta}=8\pi\sigma diag[-1,1,1,1][/math] It states that [math] \sigma [/math] is the energy density. That is the major difference between this theory (and I believe what is the only thing that can be derived from the Riemann) is that [math] \sigma [/math] isn't the energy density of the field. You can call it the density of the quintessence if it makes you feel better but the energy density we are familiar with has to be the difference between the cosmological constant and [math] \sigma [/math]. No difference=no energy=uniform Euclidean scalar field=uniform density quintessence field=flat space-time. If you want energy, then there must be a decrease in the scalar value of [math]\sigma[/math] away from the scalar value of the cosmological constant. Edit: Just to point it out, the tensor above is a rank 0 tensor with constant scalar values. This is showing that in a scalar interpretation, the Einstein tensor can turn into a rank 0 tensor with non-zero components.. The metric signature of [math]diag[-1,1,1,1][/math] and the definition of "energy" in General Relativity are mutually exclusive so the [math]\sigma[/math] cannot be the energy density with which we are familiar with.

I did't mean to imply I am splitting the cosmological constant in two, just that the dynamical portion (Einstein tensor) becomes a rank 0 tensor with scalar values equal to the cosmological constant for flat space-time. Here is where I think the difficulty arose concerning scalar fields in GR: Normally for [math]\alpha u +\beta\frac{\partial u}{\partial n}=g[/math] we see that [math]\beta\frac{\partial u}{\partial n}[/math] is some derivative of [math]u[/math] with respect to something else. Suppose we now have an equation of two of these scalar fields, which is [math]\gamma u +\eta\frac{\partial u}{\partial n}+ \alpha u +\beta\frac{\partial u}{\partial n}=g[/math] where for what want to use the equation for it appears physically that [math]\eta\frac{\partial u}{\partial n}=0[/math] and that [math]\gamma u[/math] is sooooo tiny that it has no bearing in our solar system. If we have no need for [math]\gamma u[/math] then we might be tempted to ignore the required [math]\alpha u[/math]. The difficulty with this though, is if we ignore [math]\alpha u[/math], what exactly are we finding the partial derivative of in [math]\beta\frac{\partial u}{\partial n}[/math] and in reference to what? The easy way out conceptually (but not formulaically) is to simply take partial derivatives of one dimension with respect to the others. If there is no partial derivative of one dimension with another (they aren't functions of each other), you simply have a higher rank tensor that now appears as a Euclidean rank 0 tensor with no scalar values.

It does seem that way to me. I was using [math]\Lambda[/math] in the sense of the scalar value, and meant [math]\Lambda^1[/math] as representing the magnitude of the cosmological constant (which as you say is not dynamical) but was considering [math]\Lambda^2[/math] as a rank 0 tensor which, when perturbed, becomes the dynamical higher rank 2 Einstein tensor. I think some of the confusion of what I am stating stems from there being no hard definition of what it means when a tensor "vanishes". Take for instance equation 1.2 from http://eprints.ma.man.ac.uk/894/02/0-19-852868-X.pdf [math]\alpha u + \beta \frac{\partial u}{\partial n}=g[/math] If we set [math]\alpha u=0[/math], which was a rank 0 tensor, and then [math]\mid\beta \frac{\partial u}{\partial n}\mid\rightarrow 0[/math], which is a higher rank tensor, would we define that as the higher rank tensor "vanishing"? If [math]\alpha u \neq 0[/math], but still [math]\mid\beta \frac{\partial u}{\partial n}\mid\rightarrow 0[/math], do we still consider the higher rank tensor to have "vanished" if the rank 0 tensor remains? So my main problem is the a priori assumption that when the Einstein tensor "vanishes" there is no rank 0 tensor remaining. I don't think the equation (or physical evidence) supports this. So for my post #3 where MTW "redefine" the Einstein tensor. [math]"G_{\alpha\beta}"=G_{\alpha\beta}+\Lambda g_{\alpha\beta}[/math]. It seems to me that it was redefined in order to ignore that there is a rank 0 tensor remaining after [math]G_{\alpha\beta}[/math] "vanishes".

I had someone in another forum (where speculations aren't allowed so have to be careful how one phrases a question) pose the following, which is something I had not considered before: I was aware of Lagrangian mechanics, but not aware of this derivation. The two formulas read [math]\frac{1}{16\pi} R\sqrt{-g}[/math] and [math]\frac{1}{16\pi}(R+2\Lambda)\sqrt{-g}[/math] which is interesting in that the theory is founded upon [math]L=T-V[/math], where T is the kinetic and V is the potential of the system. In a system where the baseline is represented by [math]\Lambda^V-\Lambda^T[/math] this would seem to mean that with no curvature there is no Lagrangian. It would require a change in the magnitudes of the scalar values of the [math]\Lambda^T[/math] to create it (which would change R above). In other words [math]\frac{1}{16\pi} R\sqrt{-g}[/math] with [math]R\rightarrow 0[/math] . [math]\frac{1}{16\pi}(R+2\Lambda)\sqrt{-g}[/math] with [math]R\rightarrow -2\Lambda[/math]

Thanks, I have looked into it a bit but takes time to separate out the terminology from where it is derived in a proof. As in "constant scalar curvature" giving [math]R=4\Lambda[/math]. As an example, the weak field approximation for Newtonian gravity is normally derived from [math]g_{\mu\nu}=\eta_{\mu\nu}-\epsilon_{\mu\nu}[/math] where [math]\eta_{\mu\nu}=-1[/math] and [math]-\epsilon_{\mu\nu}[/math] is some tiny perturbation. Keeping normal GR notation, the way I am proposing would start out with flat space time as [math]-\Lambda^1+\Lambda^2=0[/math] instead of just a -1. A small perturbation of [math]\Lambda^2[/math] would be used to generate the field. A bit less exciting than deSitter space, but lots to go over in the future.

Yea, sorry about that. It isn't anything other than a constant multiple of the metric, same as Lambda. I just used a different symbol since most people that understand Lambda already have preconceived notions of its magnitude. That empirical magnitude is in reference to the magnitude of the Einstein tensor. Since magnitude is one of the cosmological constant problems, I am trying to take this back to just tensors, scalars and first principles. In a nutshell, all I am stating is that for flat spacetime, no cosmological constant, the Einstein tensor vanishes, Guv->0 with cosmological constant, Guv->Lambda guv I just used different symbols above to attempt a proof. (What happened to the LaTex?) [math]LaTex[/math] (Edit: Nevermind, this one works) [tex]LaTex[/tex] [itex]LaTex[/itex] I guess I would be stating that Ricci-flat manifolds and Einstein manifolds are actually the exact same thing. Let me retract that last statement. I am proposing Ricci-flat manifolds and Einstein manifolds are the exact same thing for flat spacetime, but not curved. (Wow, a "Reply to this topic" is added as an edit to the last post automatically)

Attempting to disprove this theory, if you are able to help and catch any mistakes, much appreciated... [math]G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}[/math] Einstein tensor vanishes if and only if the Ricci tensor vanishes, only for Minkowski space [math]g_{\mu\nu}=diag[-1,1,1,1][/math] and only if [math]Ricci=\Lambda g_{\mu\nu}[/math]: [math]G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=0[/math] [math]\Omega g_{\mu\nu}-L_{\mu\nu}=G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=0[/math] [math]L_{\mu\nu}=\Omega g_{\mu\nu}[/math] [math]\Omega g_{\mu\nu}-\Omega g_{\mu\nu}=G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=0[/math] [math]\Omega g_{\mu\nu}-\Omega g_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=0[/math] [math]\Omega g_{\mu\nu}+\frac{1}{2}R g_{\mu\nu}=R_{\mu\nu}+\Omega g_{\mu\nu}=0[/math] [math]R_{\mu\nu}=-\Omega g_{\mu\nu}[/math]

Wikipedia isn't good for a cited reference, but can be adequate for introduction to subjects. If you are wondering about the vectors shown above and how they relate to manifolds, in this theory they are the vector space which you can introduce yourself to here: Vector Space These vectors are what we currently understand to be forces, which is why a constant scalar field with orthogonal vectors would seem to be a "pressure". Another thing to keep in mind is that what someone may define as a scalar would actually seem to be a magnitude in the tangent space. Take the examples given here. where it is stated "since the LHS is a vector and the RHS a scalar." As understood from the above post, the scalars |xi| shown as components are actually magnitudes of partial derivatives of the curvature of the manifold. These scalar magnitudes are different from the absolute scalars shown in the above two dimensional field (which is why the Cosmological Constant in flat Minkowski space doesn't seem to make mathematical sense otherwise). If the vectors have no magnitudes then there is no force so it isn't something normally stated when introduced to the history of field theory. These absolute scalars in this theory could be previously argued as unobservable, however I will argue that evidence is building that they are required to exist in order to make sense of dark energy and the cosmological constant.

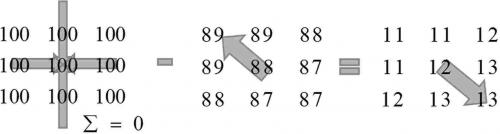
Going to continue here a bit in case I can interest a couple people in the web conference... Take for example a two dimensional scalar field (note that this isn't a matrix, it is field representing scalar values at points): The first field represents a rank 0 tensor at each point, and the second field is a rank 1 tensor at each point. Note that the cosmological constant tensor Baez shows here is a four dimensional rank 0 tensor. Normally it is partial derivatives (this is where we get "fluxes" from) that occupy each component but in the case of a rank 0 tensor it is a constant, i.e. a scalar. There are no partial derivatives of a constant, so the constant scalar field results in no directional derivatives. However, we could model this as orthogonal vectors with a sum of zero, regardless of the magnitude of the scalar values. This is where the "pressure" analogy comes from that Baez speaks of: Note that the sum of the two top tensors results in a rank 1 tensor (there are more specifics I believe under what are called Nuemann boundary conditions) but you can see that even should the second tensor scalar values settle to all zeroes or all constant values, the rank 1 tensor "vanishes" and becomes solely a rank 0 tensor. There is a problem on uniqueness of how we view that sum of these tensors in the following: This is what I believe the full Einstein field equation is showing us. Geometrically, the only thing the normal Einstein tensor (a second rank tensor) seems to rely upon are the presence of partial derivatives present as components, but even should the Einstein tensor devolve to a rank 0 tensor with arbitrary values, the constant multiple of the metric (cosmological constant) would also allow cancellation of these, still resulting in no curvature. Why is this important? The argument for Newtonian gravity is that for flat space-time and slow speeds, we only need to take into consideration g00, which would simply be a -1 (Minkowski space). The theory is that in the weak field limit, a small perturbation from this -1 will come to represent, through the equivalence principle of inertial and gravitational mass, the Newtonian [math]\Phi[/math]. If we instead consider that this small perturbation would be equal to (vacuum) stress energy tensors equated to [math]\Omega g_{00}-L_{00}[/math], and taking in what I previously stated concerning the Poisson equation and Gauss' theorem, I will proceed to make some arguments concerning why we are looking for a repulsive vacuum energy that opposes attractive gravity. If you are into Lawrence Krauss lectures, starting at he goes into that there does not seem to be any natural way to cancel the value of the cosmological constant. I will be arguing with that proposition in the web conference..

True on the unresolved problem. Baez also goes into that on his cosmological constant page. I doubt it is as simple as that either, but the cosmological constant argument was introduced via differential geometry. Einstein was aware that it showed up in the full field equation, but his actual initial argument for a static universe in his paper Cosmological Considerations on the General Theory of Relativity was based on a modification of the Poisson equation for Newtonian gravity. Slight modifications of this are still used to illustrate the bizarre effects the constant would seem to have in opposing gravity. Hobson et. al. General Relativity: An Introduction for Physicists come up with [math]\vec g=-\vec \nabla \Phi =-\frac{GM}{r^2}\hat{\vec r}+\frac{c^2 \Lambda r}{3}\hat{\vec r} [/math] Let me bypass that for now, and just point out that the reason MTW "redefined" the Einstein tensor such that [math]G_{\mu\nu}^{new}=G_{\mu\nu}^{old}+\Lambda g_{\mu\nu}[/math] is because it violates the summation properties of tensors if [math]\Lambda \neq 0 [/math]. I see how this makes it easier to transfer the physical assumptions concerning the old Einstein tensor to the new, but I don't see how this rises to the same rigor that was used previously. I agree that the two tensors on each side of the equation can't be the same, but this research is based on what the proposed effects would be if we followed the equation through explicitly. By this I mean, changing the symbols so as not to confuse ourselves, if we let [math]G_{\mu\nu}^{new}=-L_{\mu\nu}[/math] and [math]\Lambda g_{\mu\nu}=-\Omega g_{\mu\nu}[/math] to get [math]G_{\mu\nu}^{old}=\Omega g_{\mu\nu}-L_{\mu\nu}[/math]. It would require a better understanding of what we can say definitively when a tensor "vanishes". Anderson and Finkelstein wrote a paper on this. I tend to favor the concept they propose: Cosmological Constant and the Fundamental Length

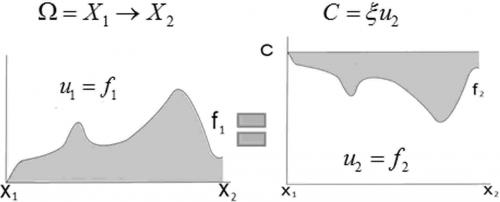
The first fundamental theorem of calculus states that, if is continuous on the closed interval and is the indefinite integral of on , then [math]\int\limits_{b}^{a} f(x)dx=F(a)-F(b)[/math] or we could write [math]\int f(x)dx=F(x)+C[/math] where C is a constant of integration, which means that there are an infinite number of antiderivatives of . We can certainly simply choose C=0 but we need to also keep in mind that the theorem makes no assumptions on the magnitudes of or C. By this I mean consider the following two plots: Since both plots have equivalent areas and if [math]f'_1=(C-f_2)'[/math] then neither the Poisson equation nor Gauss' theorem gives different answers between the two plots. By extension, I postulate that this general equivalency should also apply to differentiable manifolds and that the "Einstein tensor" is no more required to vanish for flat space-time with a multiple of the metric included than f2 is required with C. This may require unimodular assumptions but even should this turn out to not be correct (but if not, why?), it should provide some interesting comparisons with classical General Relativity and why we set vacuum as the lowest energy state =0.

True. True, but it isn't mine. MTW state the redefinition as [math]``G_{\alpha\beta}"=R_{\alpha\beta}-\frac{1}{2}Rg_{\alpha\beta}+\Lambda g_{\alpha\beta}=G_{\alpha\beta}+\Lambda g_{\alpha\beta}[/math]. They consider that with the cosmological constant the theory is no longer geometric. Alternative geometric theories of gravity in order to understand how to derive the magnitude of the cosmological constant. It seems to me that there is a simple missing case concerning parallel transport of vectors where the equation can still be considered as "geometric" even with a constant multiple of the metric included.

Ruv -(1/2) Rguv=Guv given true statement Ruv -(1/2) Rguv+Lambda guv=Guv Guv+Lambda guv=Guv false statement Going to be giving a web lecture on this next month to those interested in alternate theories, what is required to make the false statement true and what it means physically. Questions more than welcome here.

What, no Lorentzian Aether theory fans? In a nutshell I am saying that if Lorentz had realized that the Einstein field equations are only derivatives, then he would have seen his aether theory within it and predicted that not only is gravity not attractive but that the universe accelerates after matter achieves an average distance of [math]r=(\frac{6G\rho^{res}V}{\Lambda^{vac}c^2})^{1/3}[/math].

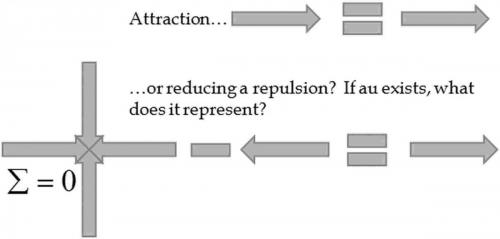
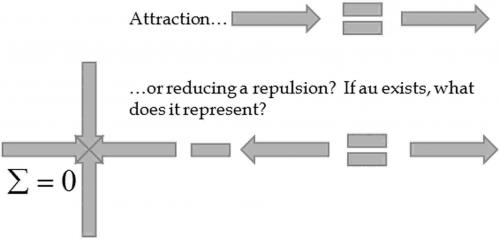
So, can [math]G_{\mu\nu}[/math] in Einstein's field equations ever be negative? In both cases, positive or negative, a difference in the density (and pressures) of a perfect fluid is equated to the curvature tensor. This is the stress energy tensor. This difference at a point causes stress outside the immediate vicinity of it, which is reflected in a change of the coordinate system. Where the coordinate system was Euclidean (flat), it no longer is. The greater the change in the density of the perfect fluid, the greater the change away from a flat coordinate system. The equations state that the curvature away from flat would be interpreted for two regions that contain a derivative of perfect fluid density into a "force" where they tend to come together. One case would consider this as an attraction between the two regions, the other would consider that the repulsion between the two regions has decreased. The defining difference between the two is the accelerating expansion. One case considers the accelerating expansion as most likely caused by an underlying energy that opposes the attractive gravity, whereas the other case simply considers the constant of integration as the point where the repulsion is no longer reduced by the presence of a change in density of a perfect fluid in another region. AFAIK, particle-wave duality is an accepted phenomenon, as is now the quantum vacuum. In addition, most of the "mass" seems to not be within the nucleus of an atom but in empty space. The density of that perfect fluid is directly tied to the density of Newtonian matter (through [math]\nabla^2 g_{00}[/math]). Therefore the majority of gravitational mass is from nothing. See starting at 19:00 I know of no way to integrate these two concepts with a positive curvature tensor, but with a negative it seems plausible.

Avoiding the maths, I am actually doing nothing but inverting the perfect fluid tensor. This would make no different predictions than the [math]\Lambda CDM[/math] model, except you would still have to add in extra curvature to account for the dark matter. This is just mathematically consistent, whereas the current model does not seem to be mathematically, logically or physically consistent. If you happen to know whether subtracting [math]G_{\mu\nu}[/math] from [math]\Lambda[/math] has ever been historically discussed, please let me know as I cannot find it and seems to be too simple of an explanation not to have been proposed before. Particles vs Waves The Einstein Field Equations Four dimensional generic functions with a constant of integration [math]R_{\mu \nu}-\frac{1}{2}g_{\mu \nu}R=g_{\mu \nu}\Lambda+G_{\mu \nu}[/math] The Fundamental Theorem of Calculus Let [math] \frac{\partial f_{1}}{\partial x_{\mu}}= - \frac{\partial f_{2}}{\partial x_{\mu}} [/math] and [math] \int f_{1}\partial x_{\mu}=\int (C-f_{2})\partial x_{\mu} [/math] Calculus has the limitation, in that a generic function with a constant of integration, has two possible ways in which to measure the exact same area. Any physical theory based off calculus must take this into consideration. If Newton's G and speed of light c are missing, assume normalized G=c=1 General Relativity Wave Theory Particles Waves [math]R_{\mu \nu}-\frac{1}{2}g_{\mu \nu}R=G_{\mu \nu}=f_{1}[/math] [math]R_{\mu \nu}-\frac{1}{2}g_{\mu \nu}R=g_{\mu \nu}\Lambda-G_{\mu \nu}=C-f_{2}[/math] Ideal Fluid Equation [math]T_{\mu \nu}=\left(\rho + \frac{p}{c^{2}}\right)\mu_{\mu} \mu_{\nu}+p\eta_{\mu \nu}[/math] Stress energy tensor of positive energy density "particle" Stress energy tensor of a reduced energy density "wave' [math]T_{\mu \nu}=[-\rho,p,p,p][/math] [math]L_{\mu \nu}=[C_\rho - \rho,-C_p +p,-C_p +p,-C_p +p][/math] Heisenberg Uncertainty Principle and de Broglie matter waves The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. Newtonian Gradient Approximation Pre1998 [math]\vec{g}=-\nabla\Phi=-\frac{GM}{r^{2}}\hat{\vec{r}}[/math] Post 1998 [math]\vec{g}=-\nabla\Phi=-\frac{GM}{r^{2}}\hat{\vec{r}}+\frac{\Lambda c^{2}r}{3}\hat{\vec{r}}[/math] [math]\vec{g}=-\nabla\Phi=-\frac{\Lambda_{\mathrm{vac}} c^{2}r}{6}\hat{\vec{r}}+\frac{G\rho_{\mathrm{res}}V}{r^{2}}\hat{\vec{r}}[/math] The accelerating expansion is due to a "dark energy", which opposes attractive action-at-a-distance Newtonian gravity, and is most likely the cosmological constant. Prior to the discovery of the accelerating expansion, all matter in the universe attracted all other matter in the universe. If one integrates the energy for the quantum vacuum down to the Planck length, the amount of energy that should gravitate (as Einstein states that all energy and mass gravitate) could be [math]10^{120}[/math] larger than what is empirically observed. The majority of mass is not in the nucleus of an atom, but in the large empty spaces outside of it. Other theory is "quintessence" (old name for the aether). If perfect fluid stress energy tensor is flipped, gravity is more of a reduced repulsion between "masses", than an increasing attraction. At the distance determined by [math]\Lambda[/math], the repulsion is no longer reduced, the symmetric wave functions are no longer affected by other wave functions, and regions that are not gravitationally bound to each other become repulsive. The amount of gravity would probably be due to wave superposition and density, and gives the value for the gravitational field strength. Should a virtual particle pair pop into existence, and then back out, they only exhibit gravitational distortion while in existence. No known technique provides a compelling solution for the cosmological constant problem. It does not appear that changing the concept of [math]G_{\mu\nu}[/math] has been attempted. My link