studiot

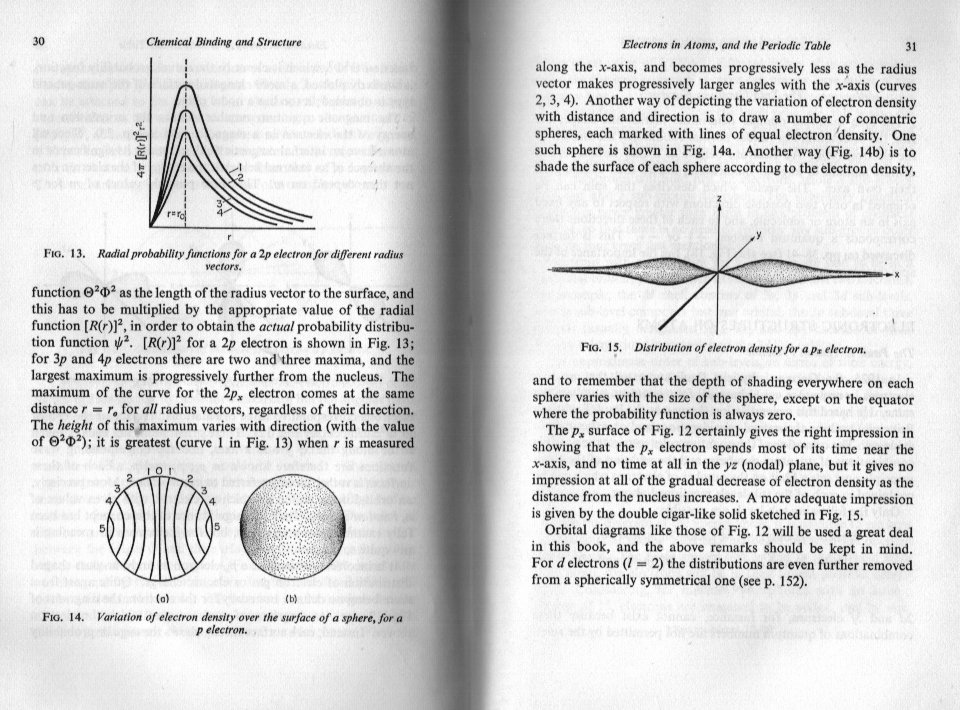
What I find confusing is that I can't see what 'your position' is. I understand that most authors skate quickly over some part of the derivation and also use different terminology that need to be sorted out. For instance your graph from the Khan academy is not a graph of probability density. Nor is it a graph of the quantities shown in arnav's parent thread. It is, and says it is, a graph of probability. In order to understand how your question is handled, it is necessary to be able to distinguish between eigenvalues and eigenfunctions of differential equations as both of these are involved in the principal and subsidiary quantum numbers n, m and l. A knowledge of symmetry, improper integrals would also help. But this is also a case of alternating the Physics and the Maths in the derivation. Authors introduce two different mathematical devices to handle the improper integrals, one is called the Probability Density the other is called the Probability Flux or Probability Current. To understand what is going on you need to start with the physics of the field of the nucleus. Do you know how to do this ?

I very much doubt if Wheeler said exactly this. For the very simple reason that a free electron accelerated to 0.85c has quite a different energy from the electron still confined within the gun of the electron source, waiting to be freed and accelerated.

Thank you, excellent answer. +1 Now we are in business. It is not necessary to be super good at differentiation and integration, just to be able to recognise what they are and what the dx and ydx means in ∫ydx One step on from this is to understand the basics of differential eqautions. Consider [math]\frac{{dy}}{{dx}} = some\,function\,of\,x = f\left( x \right)[/math] Which simply says that the derivative is some (given) function of x called f(x). This is all differential equations really are, and the solution or integration of the equation is to find the function of x that yields the given one. That is to find a function of x that when differentiated gives f(x). So rearranging dy=f(x)dx Taking the integral of both sides ∫dy=∫f(x)dx y=F(x)+C Note that variable y includes some arbitrary constant C. F(x) on its own its known as the Primitive of f(x) or the antiderivative. This is the format which you will find in swansont's excellent link to hyperphysics that he gave in his first response. This free site provides an exceptionally clear presentation of Physics and its connections to other sciences and is very well respected. http://hyperphysics.phy-astr.gsu.edu/hbase/index.html Swansont's link has several itegrals in it, which we can now explain. They are of the type [math]\int {ydx} [/math] Where y and x are different variables. So we need to change one of them into the other in order to evaluate the integral. That is express y in terms of x or dx in terms of y and dy. This format ydx is used when y is a function of x such that y =f(x) that provides a value for y at every point of interest of x. In the case of classical (wave) mechanics our variable y is sometimes called y but often the greek letter phi [math]\Phi [/math] is used and is the classical wave function. In the case of quantum mechanics this variable is psi [math]\Psi [/math] and is called the wave function. Now I have said that the wave function, or its square, is not a probability so the obvious question arises What is it ? More in a moment. But whilst we have both classical and quantum side by side, let us quickly look at your question about hyperfine splitting swansont mentioned. Splitting occurs when there is an additional disturbing or influencing force or field acting on the particle. That is additional to the base force or field that creates the (quantum) energy levels for the particle. For us the particle is the electron and the base field is the (electrostatic) field of the nucleus in which the electron moves. When an additional influence occurs (which may be self generated as with the angular momentum) or may be an external field such as the one in magnetic resonance, The original levels each split into two, one of higher and one of lower energy than the original. These can be further split to form the hyperfine splitting, but that is not really of interest here in my opinion. Splitting more generally is important in other areas such as chemical bonding where the original level splits into a higher level called an anti bonding level (orbital) and a lower level called a bonding orbital. Here the disturbing influence is the field of the second atom involved in the bonding. Splitting also ocuurs in classical situations where we modulate a classical wave with a second wave to obtain new waves of higher and lower frequencies (and therefore energies). OK back to your question and the second part. What is the wave function and what is its connection to probability ? Well a good way to study this is to do a dimensional analysis. A probability is a pure number and has no dimensions. The dimensions of the wavefunction are rather odd because they are not 'fixed', but depend upon the dimensions of the space you are working in. Again swansont has noted this very briefly. In one dimension (x) the wavefunction has dimensions [math]\sqrt {\frac{1}{{length}}} \;ie\;{L^{ - \frac{1}{2}}}[/math] In two dimensions (x,y) the wavefunction has dimensions [math]\sqrt {\frac{1}{{area}}} \;ie\;{L^{ - \frac{2}{2}}}[/math] In three dimensions (x,y,z) the wavefunction has dimensions [math]\sqrt {\frac{1}{{volume}}} \;ie\;{L^{ - \frac{3}{2}}}[/math] So neither the wavefunction nor its square are pure numbers. So they cannot by themselves be probabilities. OK so what do we do about this ? Well the method of dimensions says that if we multiply by two quantities together the dimension of the product is the product of the dimensions. That is dimension (A . B) = dim(A) . dim(B) So if we square the wavefunction to get rid of the square root and multiply by the a length or an area or a volume as appropriate we will obtain a pure number. and the differentials dx, dA and dV have the appropriate dimensions. That is how and why we form one of the integrals [math]\int {{\Psi ^2}} dx[/math] [math]\int {{\Psi ^2}} dA[/math] [math]\int {{\Psi ^2}} dV[/math] Now we have a pure number all that is left to do is to scale it into the appropriate range for a probability that is a number between 0 and 1. This process is called normalisation. This is why the probability must always be associated with a region of linear, aerial or volumetric space. Sorry it was so long and rambling but I hope it helps. F

Hello. The electron can only be at the closer point of the nucleus only on the electronic layer 1 (n1). Its probability distribution being on the layer itself. No? Or do you want to talk about the probability of distribution of the electron on the different electronic layers which would be very important on the layer 1 (at the most near the nuclei) rather than on a higher electronic layer further away from the nucleus? Perhaps you should read what swansont posted before posting confusing material like this. The nucleus has a physical size, so sure. The electron interacts electromagnetically and the fact the the electron can be found there accounts for the large hyperfine splitting of the s state as opposed to the p states, where the wave function has a node, and so doesn’t have nearly as strong an interaction. In alkali atoms the hyperfine splitting of the ground state is hundreds of MHz to >1 GHz, while the excited p-state is significantly smaller

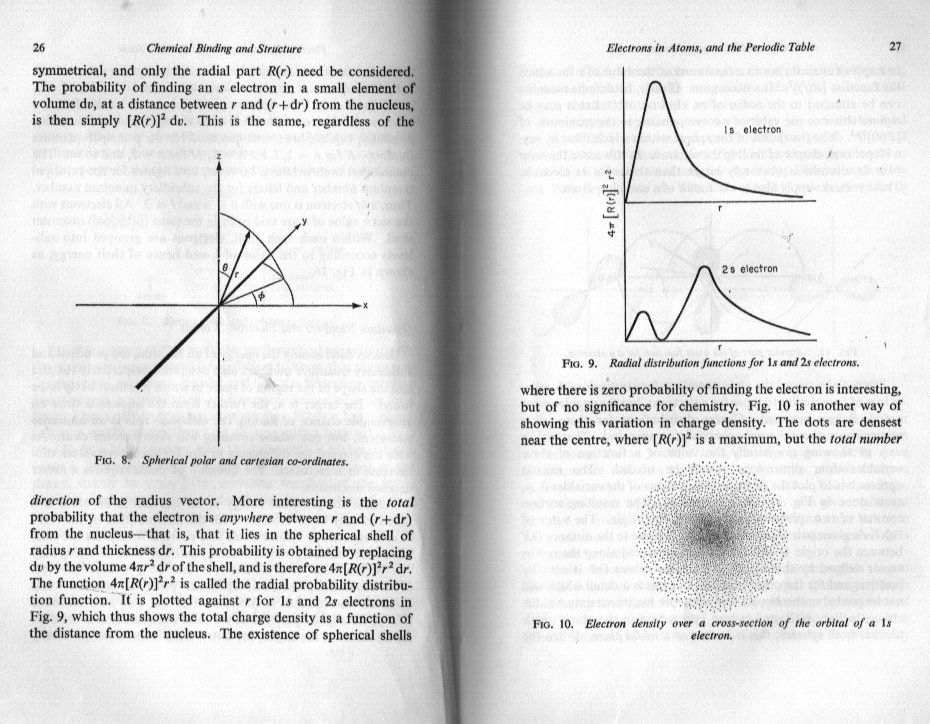
graph (b) that you posted is a graph of 'probability density' against distance from the centre of the nucleus. This is not the probability of finding an electron at a given point on the distance axis. Clearly this would always be 1, if you waited long enough. That is to say the electron will eventually be passing through this point (it will never be stationary there) so if you made your time frame long enough you would always momentarily spot the electron at some time or other. In order to explain exactly what probability density means it would be helpful if you would answer a couple of questions. Have you done enough calculus to know what a derivative (or differential) and an integral are ? Have you learned about mass, length and time as dimensions or units (called MLT) ?

It's a limit as dv tends to zero.

Are you sure you fully understand it ? You book does not say electron probability density or actual probability density on those graphs, which are basically the same as I posted. I basically agree with you, +1 , but there is yet more to it than this, though swansont's terse replies are not actually wrong, just a bit short on explanation which is implied in the physics and maths.

Remember we are discussing the proposition that the Universe is not old enough to have evolved the complexity of life we observe. This proposition is supported by a very elementary calculation of the most probably time it would take to type out a simple phrase in English, by hitting the keys at random. No one has yet point out the most elementary flaw in this argument. The phrase being Which has 15 characters. The chance of this occuring as the first 15 characters typed is exactly the same as the chance of it being the (283 x 1018 to (283 x 1018 +15)) characters. So just like the person who wins the lottery with their first ever ticket, the Universe could be lucky and not need to wait at all. I would observe that the central limit theorem does not apply to chemical reaction rates or times.

Here is an explanation with simpler maths than swansont's link that is suitable for high school level. Start reading at the star in the first attachment.

Transport Phenomena Bird,Stewart and Lightfoot. Fundamentals of Momentum, Heat and Mass Transfer Welly, Wicks and Wilson. Both from Wiley. Most of my stuff is to do with liquids including this one (Sorry I can't lay my hands on it to check at the moment) Dynamics of Fluids in Porous Media Bear There is a Dover edition of this. For dust in large scale vortices have a look at atmouspheric dynamics and meterology in you library. They should have something about this.

Don't be sorry, you are absolutely correct and I should have known better. But I get little chance to practise my German these days and the 'ei v ie' mistake is probably the most common for an Englishman.

It's only a passing point since we all seem agreed that it is an inappropriate example, for various reasons. I thought it was pointing out that any number of trials from 2 to infinity are not necessarily equivalent if they comprise n repetitions of the same trial by the same agents or n attempts at one trial by different n different agents.

Thanks for that. Interesting reply since we have 1914 - 1918 and 1939 - 1945 The only Brockhall I can trace is a small village in Lancashire. The 'Drielanderpunkt' is point where the borders of 3 countries meet. So you can step from Germany to Belgium to the Netherlands around it. On the German side there is nothing but wooded country. On the Dutch side there is a small tourist park. On the Belgian side there is the war memorial commemorating the 1944 - 1945 war and more wooded countryside. Until I saw this I never really thought about it, but rather assumed that everyone had the same dates for these most significant wars. Interesting that America didn't enter ww1 until 1917, but you count it from 1914, yet counts ww2 from 1941, not 1939.

Well Arete is making the point specifically about genetic processes, which are heavily multifactorial. I'm glad Arete chimed in because (s)he knows so much more about this than I do, which is why I was waffling generalities. But yes the monkeys are an elementary (unitary or single factor) process and evolution, which depends upon genetics, is very multifactorial. And, of course, the statistics of multifactorial processes is quite different from that of elementary ones, due to interactions between the factors. Swansont has also pointed this out, but I disagree with his interpretation of 'infinite' as applied to monkeys. As I understand this it is a classic statement of the probability which is a limit to infinity of repeated trials of a single factor. ie infinite trials. It is not infinite monkeys all typing at once. This difference clearly shows up in statistics, which does not take the time for a trial into account - rather like thermodynamics not taking the rate of a chemical reaction into account. @MarkE It is a misuse of statistics to make the mistake of infinite repetitions to measure time, as is the direct comparison of elementary and multifactorial processes timewise. Out of interest I said 'random' is an adjective and needs a noun to complete its definition of use. An example is the difference of use in the two phrases A random process A random number

I think that is an oversimplification. I seem to remember seeing a calculation leading to the reason for the magnetic containment for the minimum sized ball of hydrogen or helium that would be necessary to spontaneously initiate self sustaing fusion.

An interesting historical point. Would some Americans like to comment on what they regard as the dates for ww1 and ww2 ? I ask because there is a memorial to the 1944 - 1945 war at the 'Drielanderpunkt'.

I'm gald you found something useful in my offering. However you should avoid this myth that ionic bonds are 'stronger than covalent ones'. Some are , some are not. The hardest natural substance known is a covalent crystal and is used to make special scientific equipment for containing very very high pressures (greater than at the base of the solid part of the Earth) called the diamond anvil. As John and exchemist are noting there are also situations of intermediacy where a bond is mostly ionic (covalent) but a little bit covalent (ionic). As regards your original question, Perhaps you should study the reaction of quicklime with water to produce slaked lime. Although bonding other aspects of physchem are very modern and greeat fun I still urge you to get a good grasp of 'the stuff of matter'. Chemistry is very much about the stuff of matter and how it behaves and the theory follows knowledge of this, rather than the other way round. Yes I know there are advanced chemists who will tell you about nucleophilic reaction sites and so on , but I guarantee they have a good knowledge of 'stuff' and its behaviour to work from.

We were either facing the threat of war or at actual war during the 1950s, 1960s and 1970s I was in Hungary at the beginning of the 1956 uprising. So you continue to demonstrate my point.

You can't be serious ? The examples of war or the threat of war or the desire to win (or just not loose) a war spawning game changing developments are legion and go right back into antiquity. I already provided some examples, but since you have introduced the tank as an example let us examine its history. The tank was conceived and introduced in ww1 where the primitive originals are said to have made a difference, although late into the war. The tank was a significant factor in the first half of ww2, but by the end had become militarily obsolete by the successful introduction of anti tank rockets onto the worlds most successful military aircraft ever. After the war the company that invented this aircraft attempted to follow it up with a commercial airliner based on it. Not only was this airliner a tragic technological failure, it finally broke the company that made it.

Fair enough. Thanks for the correction to my Hector.

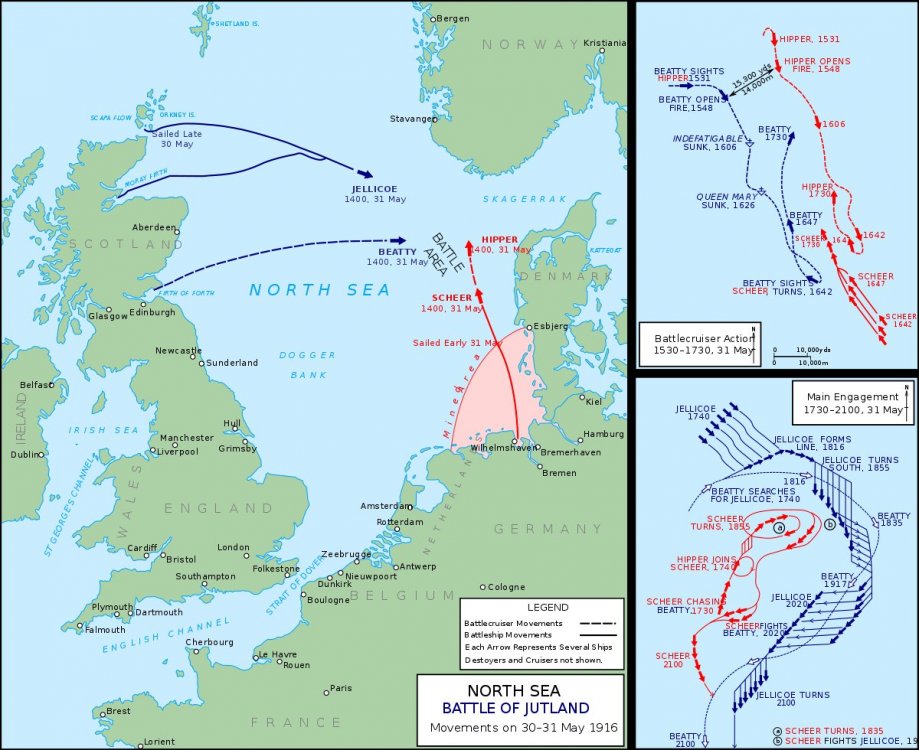
Thank you for the greater detail. +1 As I understand the battle of Salamis, it was the same tactics of 'bottleneck' used by the Spartans at Thermopylae and by Hector at the bridge. Whereas Jutland was an open water manouvering by both sides.

So all this discussion of the relationship between ww1 and ww2 is interesting but a bit off topic since the actual OP question was To which my answer is that despite Hans' points supporting the pros of the proposition, he has not weighed them against the cons opposing it. And there is one very strong con. Historically, the periods of rapid technological advance have coincided with military imperatives in many cases. So the canon replaced the trebuchet, the gun replaced the bow and arrow, the rifle replaced the musket, the shell replaced the solid projectile, I have not tried to list con points but the weighing up process should be undertaken.

I think CharonY has shown that it was more somplicated than your simplified version. Alos I note that in ww1 Germany had no imperialist ambitions in Europe. That is it did not enter the war to gain terrority but because of its obligations to someone else. This was clearly never true of A Hitler and ww2 who definitely wanted to conquer Europe at least. So it cannot be that ww2 was jjust a continuation of ww1 and the ambitions of an entirely different regime. Sure the Hitler egime used every resentment going to fan the nationalist flames. But they did not continue someone else's lost war.

Good job they didn't pass it down the line then. Naval tactics from 1815 consisted of 'line of battle' wooden sail-warships sailing past each other firing broadsides. Successful tactics 100 years later with gun turrets on motorised steel ships were rather different.

Thank you for knowing more than I did. +1